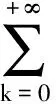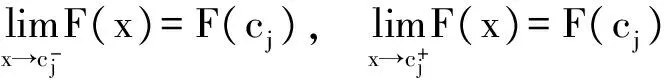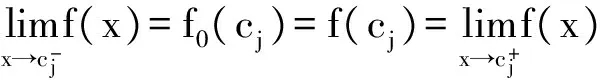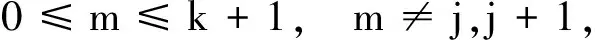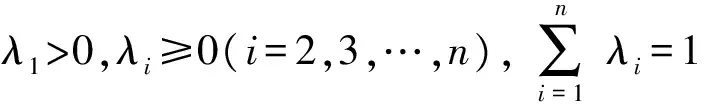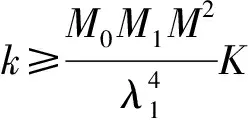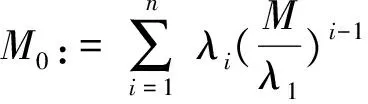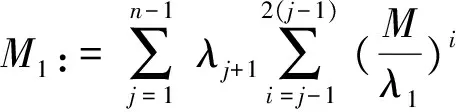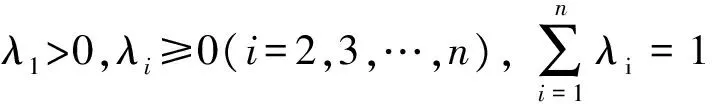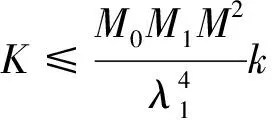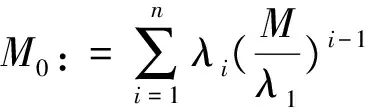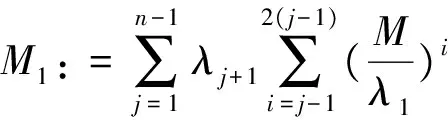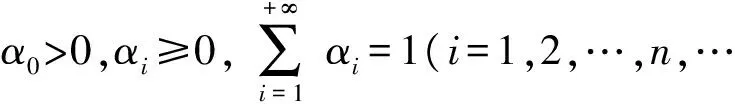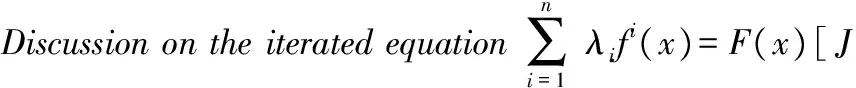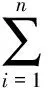多项式型迭代方程解的存在性
石勇国, 刘 娜, 龚小兵*
(1. 内江师范学院 数学与信息科学学院, 四川 内江 641199; 2. 成都工贸职业技术学院 经贸管理系, 四川 成都 611731)
多项式型迭代方程解的存在性
石勇国1, 刘 娜2, 龚小兵1*
(1. 内江师范学院 数学与信息科学学院, 四川 内江 641199; 2. 成都工贸职业技术学院 经贸管理系, 四川 成都 611731)
许多关于多项式型迭代方程的结果,如解的存在性、惟一性和稳定性等都是在已知函数为单调函数的假设条件下得到的.借助讨论迭代根时使用的特征区间的思想,在已知函数为非单调函数情形下给出了多项式型迭代方程解的存在性.
迭代函数方程; PM函数; 非单调性; 延拓
多项式型迭代方程
λ1f(x)+λ2f2(x)+…+
λnfn(x)=F(x), x∈S
(1)
是一类重要的函数方程[1-4],迭代根和不变曲线等问题都可以转化为此类方程,其中f:S→S为未知函数,F:S→S为已知函数,fi是f的i次迭代,即
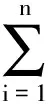
(2)
有递增解.虽然关于方程(1)和(2)已有许多很好的研究结果,但均是在F单调的情形下给出的.本文利用文献[20]的思想,在F非单调的情形下在R上研究了方程(1)和(2).首先给出了这2个方程有解的条件,再利用文献[18-19]的结果,通过延拓的方法给出了方程(1)和(2)的非单调连续解.
1 预备知识
令I:=[a,b],其中a,b∈R.设C(I)是I上所有实连续函数构成的集合.如文献[21],令
C(I,I):={f∈C(I):f(x)∈I,∀x∈I},
C+(I,I):={f∈C(I,I):f(a)=a,f(b)=b}.
对-∞≤m≤M≤+∞,定义
C(I;m,M):={f∈C(I,I):
m≤f[x1,x2]≤M,x1≠x2∈I},
C+(I;m,M):={f∈C+(I,I):
m≤f[x1,x2]≤M,x1≠x2∈I},
其中
是f的一阶差分.
如文献[20],对连续函数F:I→F(I),如果F在内点x0的某个邻域内严格单调,则称x0∈I为F的单调点,否则称内点x0为F的非单调点或简称fort.如文献[22]中的定义,如果F在区间I上只有有限个非单调点,则称F是I上的一个PM函数或逐段严格单调函数.用S(F)表示连续函数F在I上的所有非单调点构成的集合,PM(I)表示I上所有逐段严格非单调函数构成的集合.令
PM(I,J):={f∈PM(I):f(I)⊂J},
其中I和J都是区间.
设F∈PM(I)和S(F)={c1,c2,…,ck}且
c0:=a 如果区间I的子区间Ij:=[cj,cj+1](0≤j≤k)满足F(I)=F(Ij),则称Ij:=[cj,cj+1]为F的特征区间[20].注意函数F在子区间Ij上是单调的. 定理 2.1F是给定的定义在区间I上的逐段严格单调函数,子区间Ij是F的特征区间,如果函数f0:Ij→Ij是方程(2)(或(1))限制在特征区间Ij上的一个连续解,则如下定义的函数f:I→I: (3) 其中 (4) 是方程(2)(或(1))在区间I上的一个连续解. 证明 首先针对方程(2)进行证明.注意到f0定义在特征区间Ij上并且F(I)=F(Ij),所以f(x)定义有意义.接下来证明如(3)式定义的函数f满足方程(2).事实上如果x∈Ij,结论显然成立,即 (5) 如果x∈IIj,则由(4)式和特征区间的定义知 成立.所以由(3)式定义的函数f是方程(2)的解. 事实上,由(3)式定义的f在I上还是连续函数.下面给出其连续性的证明.不失一般性,假设0 和 因此 所以f在点cj连续.同理,函数f在点cj+1也连续.进一步,如果存在cm满足 或 则同证明f在点cj连续类似可证明f在点cm连续.如果 或 则由F(x)在区间I上连续和J(x)在[F(cj),F(cj+1)](或[F(cj+1),F(cj)])连续知f在点cm连续. 对于方程(1)的证明类似于文献[20].证毕. 利用文献[18]中的定理4.2和4.3,给出如下关于方程(1)有非单调解的2个结果. 其中 则方程(1)在区间I上有连续解,其中E(Ij;0,M,k,K)的定义参见文献[18]. 证明 由文献[18]的定理4.2,方程(1)在区间Ij上有连续解.由定理2.1知方程(1)在I上有解.证毕. 其中 则方程(1)在区间I上有连续解. 利用文献[18]中的定理4.3,证明与推论2.1类似. 利用文献[19]中的定理2.1,给出如下关于方程(2)存在非单调解的结果. 证明 由文献[5]中的定理2.1知方程(2)在特征区间Ij上有连续解f0.由定理2.1得方程(2)在I上有连续解.证毕. [1]BARONK,JARCZYKW.Recentresultsonfunctionalequationsinasinglevariable,perspectivesandopenproblems[J].AequationesMath,2001,61(1):1-48. [2]KUCZMAM,CHOCZEWSKIB,GERR.IterativeFunctionalEquations[M].Cambridge:CambridgeUnivPress,1990. [3]TARGONSKIG.TopicsinIterationTheory[M].Göttingen:Vandenhoeck&Ruprecht,1981. [4] 张景中,杨路,张伟年. 关于函数方程的若干进展[J]. 数学进展,1995,24(5):385-405. [5]DHOMBRESJG.Itérationlinéaired’ordredeux[J].PublMathDebrecen,1977,24(3/4):177-187. [6]JARCZYKW.Onanequationoflineariteration[J].AequationesMath,1996,51(3):303-310. [7]MATKOWSKIJ,ZHANGW.Onlineardependenceofiterates[J].JApplAnal,2000,6(1):149-157. [8]MUKHERJEAA,RATTIJS.Onafunctionalequationinvolvingiteratesofabijectionontheunitinterval[J].NonlinearAnal,1983,7(8):899-908. [9]MUKHERJEAA,RATTIJS.OnafunctionalequationinvolvingiteratesofabijectionontheunitintervalII[J].NonlinearAnal,1998,31(3):459-464. [10]TABORJ,TABORJ.Onalineariterativeequation[J].ResultsMath,1995,27(3):412-421. [11]YANGD,ZHANGW.Characteristicsolutionsofpolynomial-likeiterativeequations[J].AequationesMath,2004,67(1):80-105. [12]MALENICAM.Onthesolutionsofthefunctionalequationφ(x)+φ2(x)=F(x)[J].MatVesnik,1982,6(3):301-305. [13] 赵立人. 关于函数方程λ1f(x)+λ2f2(x)=F(x)解的存在惟一性定理[J]. 中国科学技术大学学报,1983,32(S1):21-27. [15]MAIJ,LIUX.Existence,uniquenessandstabilityofCmsolutionsofiterativefunctionalequations[J].SciChina:Math,2000,A43(9):897-913. [18]ZHANGW,NIKODEMK,XUB.Convexsolutionsofpolynomial-likeiterativeequations[J].JMathAnalAppl,2006,315(1):29-40. [19]KULCZYCKIM,TABORJ.IterativefunctionalequationsintheclassofLipschitzfunctions[J].AequationesMath,2002,64(1):24-33. [20]LIUL,GONGXB.Thepolynomial-likeiterativeequationforPMfunctions[J].SciChina:Math,2016,A59(1):1-11. [21]XUB,ZHANGW.Decreasingsolutionsandconvexsolutionsofthepolynomial-likeiterativeequation[J].JMathAnalAppl,2007,329(1):1160-1170. [22]ZHANGW.PMfunctions,theircharacteristicintervalsanditerativeroots[J].AnnPolonMath,1997,65(2):119-128. 2010 MSC:39B12; 37E05; 54C60 (编辑 周 俊) Extension of Solutions of Polynomial-like Iterative Equations SHI Yongguo1, LIU Na2, GONG Xiaobing1 ( 1.DepartmentofMathematics,NeijiangNormalUniversity,Neijiang641199,Sichuan2.DepartmentofEconomicandTradeManagement,ChengduIndustryandTradeCollege,Chengdu611731,Sichuan) Most of known results such as existence, uniqueness and stability for polynomial like iterative equations are given under the assumption that the given function is monotone. In this paper, using the idea of characteristic intervals of iterative roots we give the existence of solutions for this equation with some given nonmonotonic function. iterative functional equation; PM function; nonmonotonicity; extension 2016-12-17 国家自然科学基金(11301256)、四川省教育厅科研创新团队基金(14TD0026)和四川省教育厅自然科学基金(17ZA0217) O175 A 1001-8395(2017)04-0482-04 10.3969/j.issn.1001-8395.2017.04.009 *通信作者简介:龚小兵(1975—),男,教授,主要从事函数方程的研究,E-mail:xbgong@163.com2 解的存在性