非定常Navier-Stokes方程的一种非协调有限元投影稳定化方法

张 莉, 王彦朝, 宋卫平

(1. 四川师范大学 数学与软件科学学院, 四川 成都 610066; 2. 四川中电启明星信息技术有限公司, 四川 成都 610041)

非定常Navier-Stokes方程的一种非协调有限元投影稳定化方法

张 莉1, 王彦朝1, 宋卫平2

(1. 四川师范大学 数学与软件科学学院, 四川 成都 610066; 2. 四川中电启明星信息技术有限公司, 四川 成都 610041)

基于标准的L2投影算子，对非定常Navier-Stokes方程提出了一种非协调有限元投影稳定化方法.这种非协调有限元方法的速度/压力空间采用非协调有限元NCP1-P1.该方法不仅绕开了inf-sup条件对等阶元的束缚，也克服了高雷诺数下对流占优引起的振荡.同时，结合外推公式，将非线性问题转化为线性格式进行处理，从而减少了计算量.最后给出了详细的稳定性分析和误差分析.

Navier-Stokes方程； L2投影； 高雷诺数； 外推公式

有限元方法[1]已经成为计算流体问题Stokes方程和不可压缩Navier-Stokes方程的一种重要而有力的工具.特别地，混合有限元方法[2]备受欢迎.然而混合有限元方法的研究面临2个方面的问题:1) 要求有限元空间必须满足inf-sup条件即稳定性条件.遗憾的是工程上计算方便的等阶有限元空间不满足inf-sup条件;2) 当方程呈现对流占优时，其有限元解会出现震荡.为了克服上述困难，采用稳定化技巧的混合有限元方法应运而生.目前常用的稳定化方法主要是基于残差的稳定化方法[3-4]和基于非残差的稳定化方法[5-10].又因为基于非残差的稳定化方法不需要计算二阶导数,使得稳定化格式简单而受到更多的关注.

低阶元和等阶元在工程计算中的应用非常广泛，P. B. Bochev等[11]、Li J.[12]以及C. R. Dohrman等[13]分别对Stokes问题的低阶元和一般等阶元(P1-P1,Q1-Q1)的压力投影稳定化方法给出了详细的理论分析.Li J.等[14]和He Y.等[15]又把压力投影稳定化方法推广应用到Navier-Stokes方程，并给出了详细的理论分析和数值算例,其中，文献[14]对于瞬态的Navier-Stokes方程基于高斯积分提出了一种压力投影稳定化方法，有限元空间是采用的最低阶的等阶元.该方法虽然成功地绕开了inf-sup条件的限制，但是当雷诺数很大时，方程的解仍然可能出现不稳定性.随后,文献[16]对瞬态的Navier-Stokes方程提出了一种新的全离散粘性稳定化方法.这个方法不仅绕开了inf-sup条件的限制，同时克服了高雷诺数下对流占优引起的解的不稳定性,并且在时间计算上，每次只用进行线性计算，从而提高了计算效率.

另一方面，不可压缩流体的非协调有限元相对于协调有限元方法更加简单，单元自由度较少，并且满足局部守恒条件，从而受到更多的关注和应用.在计算的过程中，变量之间的关联仅在相邻边的中点，所形成的方程未知数较少，进而更加有利于并行计算.文献[12,14]对Stokes方程和Navier-Stokes方程提出了一类局部稳定的协调有限元方法.其速度-压力有限元空间是P1-P1元，基于高斯积分构建稳定项，得到的新的有限元格式是稳定的，成功地绕开了inf-sup条件对等阶有限元的约束.随后文献[17]又将此稳定化方法推广应用到非协调元上计算Stokes方程，其速度-压力有限元空间是非协调元NCP1-P1元，并给出了详细的理论分析和数值算例.相对于一般的非协调元Crouzeix-Raviart(C-R)元，NCP1-P1元虽然不满足inf-sup条件，但是计算更加精确.这类局部稳定的有限元方法[12,14,17]比传统的混合有限元方法更加简单、有效且不依赖于稳定化参数.

受以上讨论的启发,本文针对非定常的Navier-Stokes方程，建立了一种既能克服对流占优所引起的震荡，又能绕开inf-sup条件限制的非协调有限元稳定化方法.特别地，本文所给的投影不需要将速度或压力投影到异网格上进行计算，利用外推公式将非线性格式转换为线性格式,从而大大地减少了计算量，提高计算效率.

1 非定常Navier-Stokes问题

本文考虑如下非定常Naiver-Stokes方程

(1)

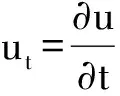
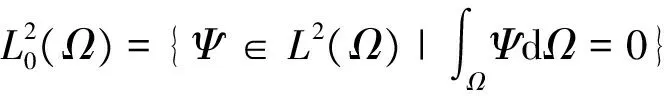
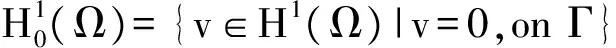
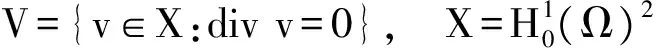
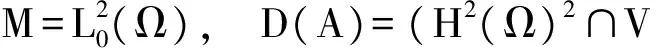
(·，·)和‖·‖0，分别表示空间L2(Ω)(或L2(Ω)2)的内积和范数,((u,v))=(u,表示和X空间的内积和范数.在空间中，|·|1=‖·‖0与‖·‖1是等价的,因此统一用‖·‖1表示|·|1和‖·‖1.

问题(1)的等价变分格式为:求(u,p)∈X×M,t∈[0,T]，对∀(v,q)∈X×M，满足关系

(ut,v)+B(u,p;v,q)+a1(u;u,v)=(f,v),

u(0)=u0,

(2)

其中

B(u,p;v,q)=λa0(u,v)+b(u,q)-b(v,p),

∀(u,p),(v,q)∈X×M,

a0(u,v)=(u,v), ∀u,v∈X;

b(u,q)=(q,·u)， ∀u∈X,q∈M,

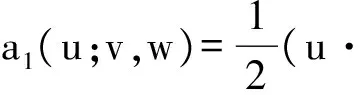
∀u,v,w∈X,

且a1(u;v,w)有如下性质：

|a1(w;u,v)|≤C‖w‖‖u‖0‖v‖0,

|a1(w;u,v)|≤C‖‖

‖‖‖.

2 非协调有限元稳定化方法

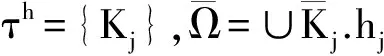
定义

∀n>0，

其中Pn(K)为单元K上所有次数小于等于n的多项式集合.

本文考虑如下的速度和压力的有限元空间:Xh=NCP1，Mh=P1，其中

NCP1={u∈L2(Ω)：u|Kj∈(P1(Kj)),

u(ξjk)=u(ξkj)，u(ξk)=0,∀Kj,Kk∈τh},

P1={P∈H1(Ω)∩M：p|Kj∈P1(Kj),∀Kj∈τh},

其中P1(Kj)表示单元Kj上所有次数小于等于1的多项式集合.由定义不难得到空间NCP1满足相容性条件：

∫Γjk[u]ds=0, ∫Γjuds=0,

和下列性质[17]:

对于任意的(u,p)∈X×M,存在(Πu，Πp)∈Xh×Mh使得

‖u-Πu‖1,h+‖p-Πp‖0≤Ch(‖u‖1+‖p‖0),

对于任意的(u,p)∈(H2(Ω)∩X)×(H1(Ω)∩M)，存在(Πu,Πp)∈Xh×Mh使得

‖u-Πu‖0+h(‖u-Πu‖1,h+‖p-Πp‖0)≤

Ch2(‖u‖2+‖p‖1),

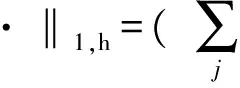
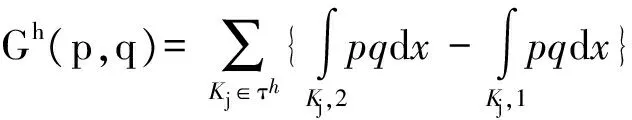
∀p,q∈L2(Ω),

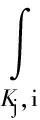
(ρhp,q)=(p,q), ∀q∈M,

‖ρhq‖0≤C‖q‖0, ∀q∈M,

‖(I-ρh)q‖0≤Ch‖q‖1, ∀q∈H1(Ω)∩M.

(3)

记

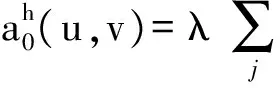
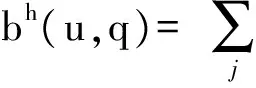
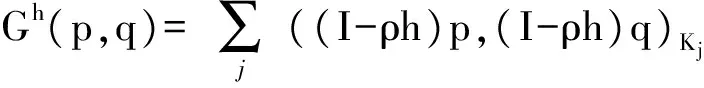
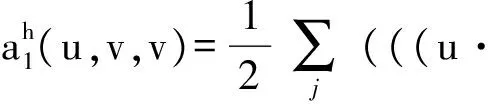
((u·)v,v)Kj),

bh(v,q)+Sh(u,v)+Gh(p,q).

定理 2.1[17-18]存在与h、λ、k无关的正常β，对任意的(uh,ph)，(vh,qh)∈Xh×Mh，使得

|Bh(uh,ph;vh,qh)|≤

C(‖uh‖1,h+‖ph‖0)(‖vh‖1,h+‖qh‖0),

β(‖uh‖1,h+‖ph‖0)≤

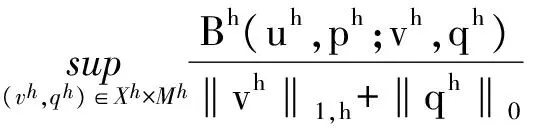
|Gh(ph,qh)|≤C‖(I-ρh)ph‖0‖(I-ρh)qh‖0.

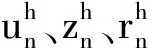
Sh(uh,vh)=α((I-πl-1)uh，(I-πl-1)vh),

∀uh,vh∈Xh,

其中,α为稳定化参数,πl-1:L2(Ω)→(Pl-1(τh))2是标准的全局或局部L2投影，且满足性质

(u,vh)=(πl-1u,vh)， ∀u∈X，vh∈(Pl-1(τh))2,

‖πl-1u‖0≤C‖u‖0, ∀u∈X,

‖u-πl-1u‖0≤Chl‖u‖l,

∀u∈X∩Hl(τh).

(4)

为了便于表述，引入如下记号和引理：

定义 2.1 对∀(u,p),(v,q)∈X×M,有

Bh(u,p;v,q)=B(u,p;v,q)+Sh(u,v)+Gh(p,q),

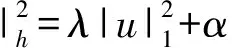
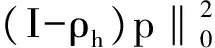
根据文献[10]，有下列稳定性结论:

引理 2.1 对于任意的ph∈Mh，存在常数β1满足:

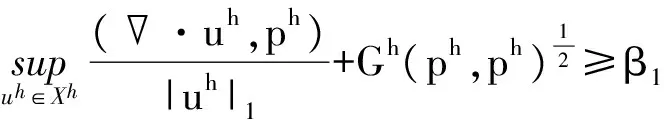
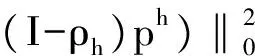
用类似于文献[7,10]的方法可以得到如下定理:

定理 2.2 对任意(uh,ph)∈Xh×Mh,有

|Bh(u,p;w,φ)|≤C|‖(u,p)‖|×|‖(v,q)‖|,

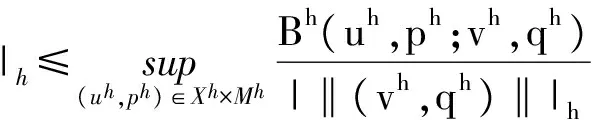
其中常数β2与h和α无关.

由此，得到(1)式的一个新的有限元稳定格式:

对∀(vh,qh)∈Xh×Mh和所有n≥1，使得

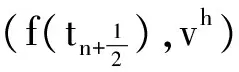
(5)

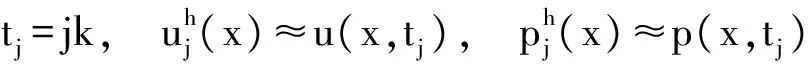
下面将详细证明格式(5)是稳定的，并且误差精度能达到O(h2+(k)4).

3 稳定性与误差分析

定理 3.1 格式(5)是稳定的，即对任意的h,k,n>0满足

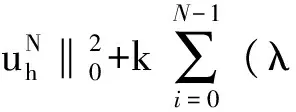
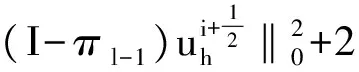
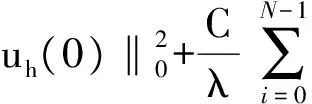
(6)

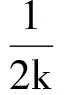
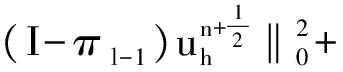
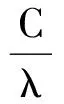
将上式两边同时对n从0到N-1求和,可得(6)式.证毕.

3.2 误差估计

定义 3.1 对任意(v,q)∈X×M,(vh,qh)∈Xh×Mh，令投影算子(Ph,Qh):X×M→Xh×Mh满足如下关系：

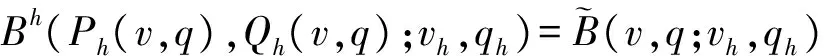
其中

引理 3.1[17-18]投影算子(Ph，Qh)满足如下性质:对∀v,q∈X×M，则

‖v-Ph(v,q)‖1,h+‖q-Qh(v,q)‖0≤

c(‖v‖1+‖q‖0),

对∀v,q∈(H2(Ω)∩X)×(H1(Ω)∩M)，则

‖v-Ph(v,q)‖0+h(‖v-Ph(v,q)‖1,h+

‖q-Qh(v,q)‖0)≤ch2(‖v‖2+‖q‖1).

定理 3.2 设u∈L∞(0,T;Hm+1(Ω))∩L∞(0,T;L∞(Ω))∩C0(0,T;H1(Ω))，u∈L∞(0,T;L∞(Ω))，ut∈L2(0,T;Hm+1(Ω))∩L∞(0,T;L2(Ω))，utt∈L2(0,T;H1(Ω))，uttt∈L2(0,T;L2(Ω)),ptt∈L2(0,T;L2(Ω))，f∈L2(0,T;H-1(Ω))，并且是方程(5)的解,则存在一个与h、k、λ无关的常数c=c(Ω,u,p,T,f)>0，对∀n∈{0,1,…,N-1}使得

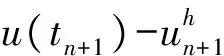
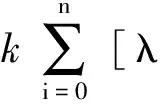
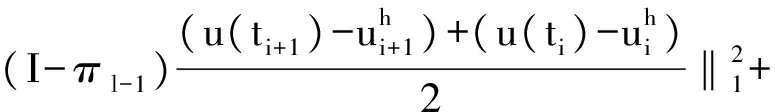
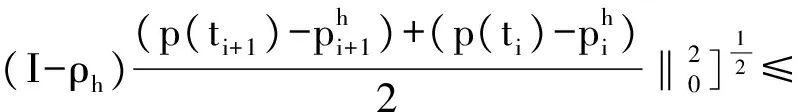
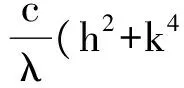
(7)

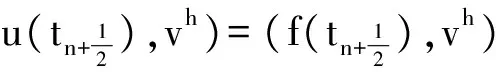
∀vh∈Xh， qh∈Mh.

(8)

(8)式减去(5)式可得

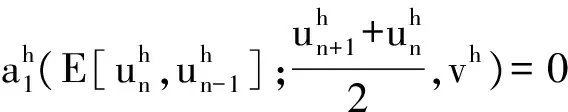
(9)

令

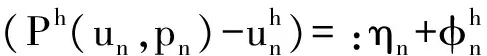
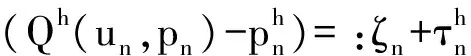
(10)

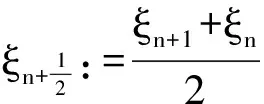
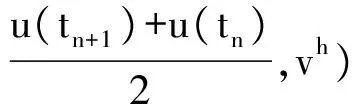
(11)

可得

Tn(u,p,vh)，

(12)

其中

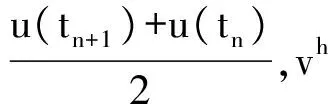
(13)

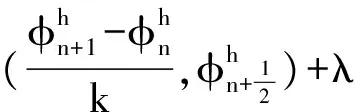
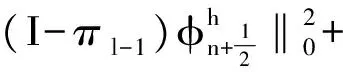
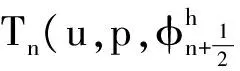
(14)

由Cauchy-Schwartz不等式和Young不等式易得

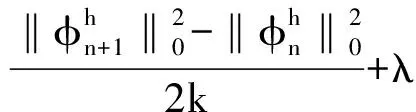
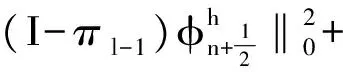
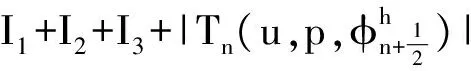
(15)

其中

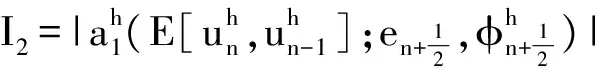
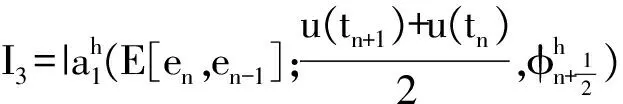
(16)

接下来估计I1、I2、I3.对I1由Young不等式得

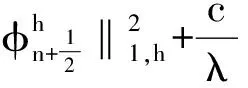
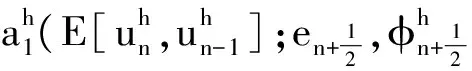
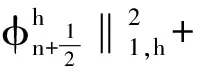
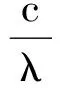
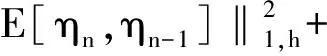
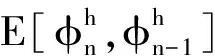
由E[·,·]的定义和u的正则性及逆不等式得

‖E[u(tn),u(tn-1)]‖1≤c，

‖E[ηn,ηn-1]‖1≤

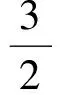
(19)

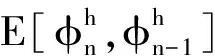
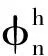
(20)

将(19)和(20)式代入(18)式，则有

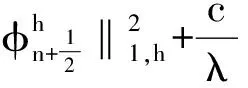
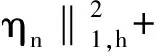
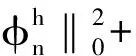
(21)

下面考虑I3的估计.由三角不等式、Young不等式以及u的正则性有

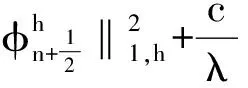
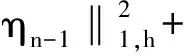
(22)

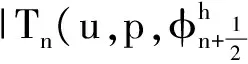
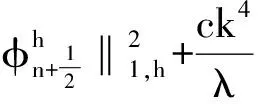
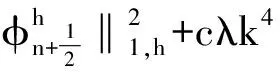
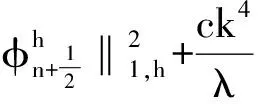
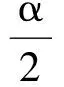
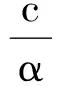
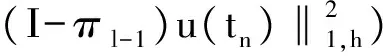
(23)

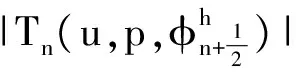
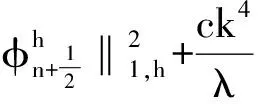
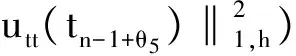
(24)

其中θ5,θ6∈(0,1).于是

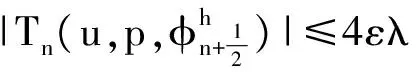
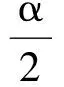
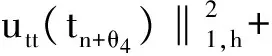
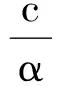
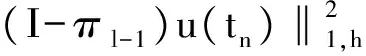
(25)

将(17)、(21)、(22)、(25)式代入(15)式,并取ε=1/20，可得

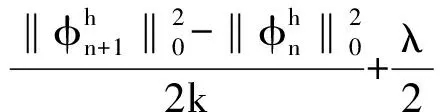
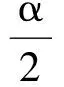
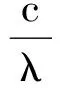
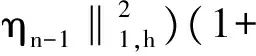
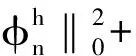
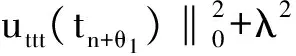
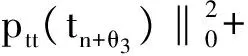
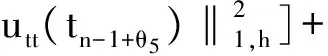
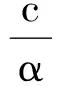
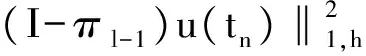
(26)

将(26)式从1到n相加，并乘以2k可得

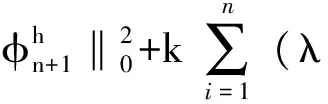
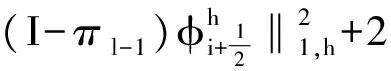
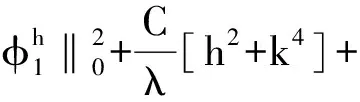
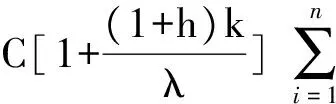
(27)

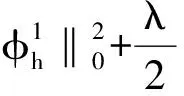
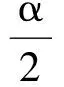
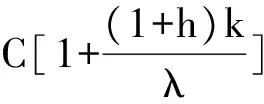
(28)

由u和p的正则性假设，三角不等式和Gronwall不等式，并综合(27)和(28)式可得(7)式.证毕.

4 结束语

本文对非定常Navier-Stokes方程提出了一种非协调有限元投影稳定化方法.速度/压力空间采用非协调有限元NCP1-P1，基本L2投影算子构建速度和压力稳定项,由此构造的有限元方法不仅绕开了inf-sup条件对等阶元的束缚，同时也克服了高雷诺数下对流占优引起的振荡.文中给出了详细的稳定性分析和误差分析,由误差估计可以得到误差精度达到了O(h2+k4).文中结合外推公式，将非线性问题转化为线性格式进行处理，从而减少了计算量提高了计算效率.

[1] GIRAULT V, RAVIART P A. Finite element approximation of the Navier-Stokes equations[C]//Lecture Notes in Math,749. Berlin:Springer-Verlag,1974.

[2] BREZZI F, FORTIN M. Mixed and Hybrid Finite Element Methods[M]. Berlin:Springer-Verlag,1991.

[3] ZHOU T, FENG M. A least squares Petrov-Galerkin finite element method for the stationary Navier-Stokes equations[J]. Math Comput,1993,60(202):531-543.

[4] DOUGLAS J, WANG J. An absolutely stabilized finite element method for the Stokes problem[J]. Math Comput,1989,52(186):495-508.

[5] BECKER R, BRAACK M. A finite element pressure gradient stabilization for the Stokes equations based on local projections[J]. Calcolo,2001,38(4):173-99.

[6] CODINA R. Analysis of a stabilized finite element approximation of the Oseen equations using orthogonal subscales[J]. Appl Numer Math,2008,58(3):264-283.

[7] BURMAN E. Pressure projection stabilizations for Galerkin approximations of Stokes’ and Darcy’s problem[J]. Numer Meth PDE,2008,24(1):127-143.

[8] FENG M, BAI Y, HE Y, et al. A new stabilized subgrid eddy viscosity method based on pressure projection and extrapolated trapezoidal rule for the transient Navier-Stokes equations[J]. J Comput Math,2011,29(4):415-440.

[9] QIN Y, FENG M, LUO K, et al. Local projection stabilized finite element method for Navier-Stokes equations[J]. Appl Math Mech,2010,31(5):651-664.

[10] 覃燕梅，冯民富，尹蕾. Navier-Stokes方程的一种等阶稳定化亏量校正有限元法[J]. 计算数学，2010，32(1):1-14.

[11] BOCHEV P B, DOHRMAN C R, GUNZBURGER M D. Stabilization of low-order mixed finite elements for the stokes equations[J]. SIAM J Numer Anal,2006,44(1):82-101.

[12] LI J, HE Y. A stabilized finite element method based on two local Gauss integrations for the Stokes equations[J]. J Comput Appl Math,2008,214:58-65.

[13] DOHRMAN C R, BOCHEV P B. A stabilized finite element method for the stokes problem based on polynomial pressure projections[J]. Inter J Numer Meth Fluids,2004,46(2):183-201.

[14] LI J, HE Y, CHEN Z. A new stabilized finite element method for the transient Navier-Stokes equations[J]. Comput Meth Appl Mech Engine,2007,197(1/2/3/4):22-35.

[15] HE Y, LI J. A stabilized finite element method based on local polynomial pressure projection for the stationary Navier-Stokes equations[J]. Appl Numer Math,2008,58(10):1503-1514.

[16] 覃燕梅，冯民富，周天孝. 瞬态Navier-Stokes方程的一种新的全离散粘性稳定化方法[J]. 应用数学与力学,2009,30(7):783-798.

[17] LI J, CHEN Z. A new local stabilized nonconforming finite element method for the Stokes equations[J]. Computing,2008,82(2/3):157-170.

[18] JING F, SU J, ZHANG X, et al. Characteristic stabilized nonconforming finite Element method for the unsteady incompressible Navier-Stokes equations[J]. Chin J Engine Math,2014,315:764-778.

2010 MSC：49J20; 49K20; 65M12; 65M60

(编辑 周 俊)

A Stabilized Nonconforming Finite Element Method Based onL2Projection for the Non-stationary Navier-Stokes Equations

ZHANG Li1, WANG Yanzhao1, SONG Weiping2

(1.CollegeofMathematicsandSoftwareScience,SichuanNormalUniversity,Chengdu610066,Sichuan; 2.AostarInformationTechnologiesCo.Ltd,Chengdu610041,Sichuan)

In this paper, we propose a new stabilized nonconforming finite element method based onL2projection for the Navier-Stokes equations with high Reynolds number. This nonconforming method use the lowest equal-order pair of mixed finite elements (i.e., NCP1-P1). The scheme not only avoids the requirement caused by the inf-sup condition but also overcomes the convection domination caused by the high Reynolds number. We transform the nonlinear problem into a linear problem using the Extrapolation formula to simplify the computation. The stability and error analysis of this method are given in detail.

Navier-Stokes equations;L2projection; high Reynolds number; extrapolation formula

2016-10-20

国家自然科学基金(11571245和11371267)、973项目子课题(2011CB301800)和四川省教育厅自然科学研究一般项目(11ZB083和

张 莉(1982—),女,讲师,主要从事计算数学的研究,E-mail:lizhang_hit@163.com

O241.82

A

1001-8395(2017)04-0435-07

10.3969/j.issn.1001-8395.2017.04.002

15ZA0031)