外差组及其通信应用

杨名慧, 文洁晶, 冯克勤

(1. 中国科学院 信息工程研究所, 北京 100193; 2. 南开大学 陈省身数学研究所, 天津 300071; 3. 清华大学 数学科学系, 北京 100084)

外差组及其通信应用

杨名慧1, 文洁晶2, 冯克勤3*

(1. 中国科学院 信息工程研究所, 北京 100193; 2. 南开大学 陈省身数学研究所, 天津 300071; 3. 清华大学 数学科学系, 北京 100084)

组合设计在通信中有着广泛的应用.综述近年来基于同步通信，防欺骗数字签名和认证、密秘共享等方面应用背景而提出的一些新型组合设计：外差组以及它的各种推广和变种.解释这些组合设计和通信应用的联系，介绍它们的构作方法和存在性方面的已知结果,以及未解决的问题.

差集合; 无逗号码; AMD码; 认证码; 分圆类; 分圆数

和组合数学许多分支一样,组合设计起源于一些游戏(欧拉36军官问题、晚宴请客……).由于工业产品制作和质量控制等方面的实验需要,组合设计从20世纪50年代开始发展.数字通信技术的进步促使组合设计在信息理论和工程方面有许多应用和密切联系.本文综述近年来由同步通信、秘密共享、数字签名和认证等方面的新问题所提出来的一种新型组合结构——外差组(EDF)及其各种推广(强外差组、广义强外差组).关于组合设计的基本知识可参见文献[1].

1 外差组及其推广

定义 1.1 设(G,+)是n阶交换(加法)群,D为G的一个k元子集合,D叫作是G中一个(n,k,λ)-差集合(DS),是指对G中每个非零元素g,方程g=x-y在D中恰好有λ组解(x,y)(x,y∈D).如果记如下的“多重”集合

Δ(D,D)={x-y:x,y∈D},

则x-y=0在D中恰好有|D|=k个:(x,y)=(a,a),a∈D,从而D为(n,k,λ)-差集合也可以表示成

Δ(D,D)=k{0}+λ(G-{0})，

(1)

这里,等式两边均表示为群环Z[G]中的元素.Z[G]中元素唯一表示成

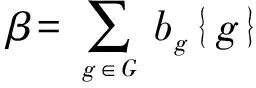
其中

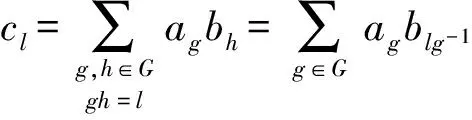
Z[G]对于上述运算为交换环.

例 1.1G=(Z7,+),则D={1,2,4}是G的(n,k,λ)=(7,3,1)-差集合.事实上,Δ(D,D)={1-1,1-2,1-4,2-1,2-2,2-4,4-1,4-2,4-4}=3·{0}+(Z7-{0}).

差集合的参数满足k(k-1)=λ(n-1).特别地,(n-1)/k(k-1)为正整数.当它不是正整数时,人们放宽一些条件,给出差集合的一些变种.下面是本文要用到的一个变种.

定义 1.2 设G为n阶交换群,D为G的k元子集合,并且0∉D.称D为G的(n,k,λ,μ)-部分差集合(PDS),是指

Δ(D,D)=k·{0}+λD+μ(G-D-{0}).

(2)

也就是说,D中每个元素在Δ(D,D)中均恰好出现λ次,G中其它非零元素在Δ(D,D)中均恰好出现μ次.由(2)式知参数满足条件k(k-1)=λk+μ(n-k-1).

例 1.2G=(Z13,+),D={1,3,4,9,10,12}.可验证D为G的(13,6,2,3)-PDS.

另一种推广是把一个集合D改用m个集合A1,A2,…,Am构成的集组.

定义 1.3G为n阶交换群,m≥2,A1,A2,…,Am为G的子集合,|Ai|=ki≥2(1≤i≤m),称{A1,A2,…,Am}为G的(n,m;k1,k2,…,km;λ)-差集组(DF),是指

λ(G-{0}).

(3)

(注意群环中的元素Δ1+Δ2指并集Δ1∪Δ2).由(3)式给出

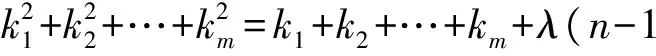
定义1.3中是每个Ai做Δ(Ai,Ai)然后将它们合并.本文要介绍的是另一种组合设计,即不同Ai和Aj(i≠j)之间的元素相减.

Δ(Ai,Aj)={x-y:x∈Ai,y∈Aj},

然后把它们合并.

定义 1.4G为n阶交换群,m≥2,A1,A2,…,Am为G的子集合,|Ai|=ki≥1(1≤i≤m),{A1,A2,…,Am}叫作G的一个(n,m;k1,k2,…,km;λ)-外差组(EDF),是指

(4)

由此式可知,A1,A2,…,Am必然两两不相交(因为0不属于上式左边),并且

λ(n-1).

如果k1=k2=…=km=k,则{A1,A2,…,Am}称为正则的(n,m;k,λ)-EDF,这时(m2-m)k2=λ(n-1).

下面是比外差组更强的组合设计.

定义 1.5 (G,+)为n阶交换群,m≥2,A1,A2,…,Am为G的子集合,|Ai|=ki≥1(1≤i≤m).{A1,A2,…,Am}叫作是G的一个(n,m;k1,k2,…,km;λ1,λ2,…,λm)-广义强外差组(GSEDF),是指对每个i(1≤i≤m)

(5)

对于这种设计,A1,A2,…,Am必然两两不相交,并且对每个i(1≤i≤m)

ki(k-ki)=λi(n-1),k=k1+k2+…+km.

进而由定义可知,如果{A1,A2,…,Am}是G的(n,m;k1,k2,…,km;λ1,λ2,…,λm)-GSEDF,则

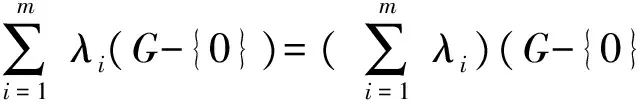
从而{A1,A2,…,Am}也是G的(n,m;k1,k2,…,km;λ1+λ2+…+λm)-EDF.

如果k1=k2=…=km=k,则λ1=λ2=…=λm=λ,这时称{A1,A2,…,Am}为G的一个(n,m;k,λ)-强外差组(SEDF).这时(m-1)k2=λ(n-1).

例 1.3 设G={g1,g2,…,gn},则{g1},{g2},…,{gn}为G的(n,n;1,1)-SEDF,这称为G的平凡SEDF,以下只对非平凡SEDF有兴趣.

例 1.4G=(Zn,+),n=ab+1.令A1={0,1,…,a-1},A2={a,2a,…,ba}.易证{A1,A2}为G的(n=ab+1,2;k1=a,k2=b;λ1=1,λ2=1)-GSEDF.

(注意对于m=2情形,{A1,A2}为G的(n,2;k1,k2;λ1,λ2)-GSEDF,必然λ1=λ2=λ,并且Δ(A1,A2)=Δ(A2,A1)=λ(G-{0})).这时k1k2=λ(n-1),特别地,当a=b时,即G=(Zn,+),n=a2+1,则A1={0,1,…,a-1}和A2={a,2a,…,a2}为G的(n=a2+1,2;a,1)-SEDF.

例 1.5G=(Z7,+),A1={1},A2={2},A3={4},A4={0,3,5,6},则{A1,A2,A3,A4}为G的(7,4;1,1,1,4;1,1,1,2)-GSEDF.

此外还有更广的组合设计,如有界广义强外差组(BoundGSEDF)等,为了节省篇幅,这里从略.

2 外差组(EDF)的通信应用

外差组最早由V.I.Levenshtein[2]于1971年提出,不过在文献[2](以及其后不少文献)中采用名称为DSS,其背景是为解决同步通信问题用来构作最优的无逗点码.后来又发现EDF及其推广GEDF可用于认证码和秘密分享[3],其中一类特殊的防欺骗认证码,叫作AMD码,是由R.Cramer等[4-5]提出.外差族(EDF)、强外差组(SEDF),及其推广GSEDF可用来构作最优的AMD码.关于这些组合设计和AMD码之间的联系在文献[6]中有系统阐述.

这里简要地介绍EDF和SEDF及其推广的组合设计和CF码以及AMD码之间的联系.

2.1 EDF和CF码[7] 设G是一个q元集合,q≥2,n≥1.Gn是由n-数组a=(a1,a2,…,an)(ai∈G)构成的集合,|Gn|=qn.Gn中a和b=(b1,b2,…,bn)的汉明距离定义为

dH(a,b)=|{i|1≤i≤n,ai≠bi}|.

Gn中每个子集合C均叫作一个q元码长为n的纠错码,C中n-数组c=(c1,c2,…,cn)叫作码字,每个码字代表某个信息经过信道由Bob发给Alice.不在C中的向量不代表任何信息.码字个数|C|=K≥2,通常小于qn,即C比Gn小.Gn中许多向量不是码字,目的是为了纠错.

除了码长n,集合S中元素个数q和码字个数K之外,另一个重要参数是码C的最小距离d=d(C),它定义为不同码字之间汉明距离的最小值,即

d=d(C)=min{dH(c,c′):c,c′∈C,c≠c′}.

综合上述,要构作码长n的q元纠错码C,码字个数K=|C|≥2,最小距离d=d(C),这些参数表示成(n,K,d)q.希望对固定的q和n,K愈大愈好(表示传输信息量大),d愈大愈好(纠错能力强).以上是纠错码的基本原理.

V.I.Levenshtein[2]研究信息传输中遇到的同步问题.考虑Bob将2个信息a=(a1,a2,…,an)和b=(b1,b2,…,bn)依次传给Alice:(a1,a2,…,an,b1,b2…,bn…),a,b∈C.但是传输中并没有an和b1之间的逗号,即Alice收到一串符号之后,不知是从何处分组,如果从a2开始的n-数组a2…anb1也是码字,Alice就译错了信息.所以,为了决定分组的逗号位置,要求对任意2个码字a=(a1,a2,…,an)和b=(b1,b2,…,bn)∈C(可以a=b),不适宜的分组ai+1,…,an,b1,b2,…,bi(1≤i≤n-1)均不是码字.满足此要求的码C叫作是无逗号码.进一步还希望:不仅不适宜的分组ai+1,…,an,b1,b2,…,bi(1≤i≤n-1)都不是码字,而且和任何码字的汉明距离都很大,即定义C的Comma-free指数为

ρ=ρ(C)=

min{dH(c,ai+1,…,an,b1,b2,…,bi):

c=(c1c2…cn),a=(a1a2…an),

b=(b1b2…bn)∈C,1≤i≤n-1}.

对于给定的q,n和ρ,希望K愈大愈好.令n-r=logqK,r=n-logqK叫码C的冗余度,希望r愈小愈好.但是文献[2]给了一个下界

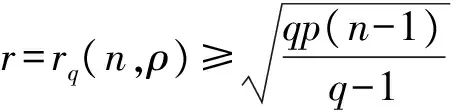
如果r达到此下界,则CF码C叫作是最优的.

设G为n阶交换群,A1,A2,…,Aq(q≥2)为G的两两不相交集合.|Ai|=ki≥1(1≤i≤m).如果{A1,A2,…,Aq}是G的一个(n,q;k1,k2,…,kq;ρ)-EDF,则文献[2]中由此可构作一个参数(n,K,ρ)q的CF码,其中K=qn-r,而r=k1+k2+…+kq(≤n),并且这个CF码是最优的,当且仅当k1=k2=…=kq=k,即{A1,A2,…,Aq}是正则的(n,q;k,ρ)-EDF,其中

r=qk,k2q(q-1)=ρ(n-1).

于是

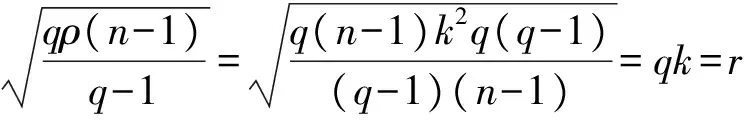
即CF码是最优的.

这就是外差组(EDF)这种设计最早的应用背景.

2.2 外差组和AMD码AMD码是一类防欺骗的无条件安全的认证码.这里的认证码是(S,G,E),其中S为信息集合,|S|=m.不妨设S={1,2,…,m}.G为n阶交换群.E为编码函数,对每个i,E(i)为G的一个子集合,并且E(i)(1≤i≤m)两两不相交.

令Ai=E(i),则A1,A2,…,Am为G的两两不相交的子集合.|Ai|=ki(1≤i≤m),则k1+k2+…+km≤n.

设Bob把信息i发给Alice,Bob在集合Ai中随机(等概率)地取t∈Ai=E(i),叫作tag(标签),把(i,t)发给Alice,t即是Bob对信息i所做的签名.Alice收到(i,t)之后,计算t是否属于Ai=E(i).由此来认证消息是否由Bob发出的,如果t∈E(i),则Alice认为消息是由Bob发出,i是Bob发给她的“真实”信息.编码函数E由Bob和Alice约定,对外人保密.

现在,Tom想把一个伪造的信息i′发给Alice.Tom随机取元素t′∈G,然后将(i′,t′)发给Alice.Alice收到后,恰好t′∈Ai′=E(i′),则Alice便认为i′这是来自Bob的信息.又若i′≠i,则Alice相信了假的信息i′.所以在t′∈E(i′)并且i≠i′,Tom便成功欺骗了Alice.Alice和Bob希望设计编码函数E使得欺骗成功概率达到最小(事实上,认证码采用许多编码函数EK,其中K为密钥,定期更换密钥).

AMD码是R.Cramer等[5]于2008年提出来的,后来的研究有文献[8]等工作.在这种认证码中,Tom的欺骗方式为采用如下简单的法则:随机选取一个固定元素g∈G,然后将Bob的每个对i的签名t都改成i′的签名t+g.

AMD码有2种欺骗策略,如果Tom只知Bob发出的tagt而事先不知Bob发给Alice的信息i,这时Tom发(i′,t′=t+g)给Alice,只有当t′∈E(i′)并且i≠i′时才欺骗成功,这叫做是弱AMD码.如果Tom知道i和t,这时向Alice发送(i′,t′),其中t′=t+g,由于Tom已知i,可取i′≠i保证i′为假信息.从而只需要t′∈E(i′)便欺骗成功.这叫作强AMD码.文献[6]中对弱AMD码和强AMD码都给出了欺骗成功的2种下界:G-下界和R-下界.达到这些下界的AMD码分别叫作是G-最优的和R-最优的.

下面是强外差族这种组合设计和最优AMD码之间的关系.

设(S,G,E)为一个AMD码,S={1,2,…,m},Ai=E(i)1≤i≤m为G中两两不相交的子集合,|Ai|=ki,文献[6]中证明了:

定理 2.1 1) 如果{A1,A2,…,Am}为群G的(n,m;k1,k2,…,km;λ1,λ2,…,λm)-GSEDF,则(S,G,E)为R-最优的强AMD码和R-最优的弱AMD码.

2) 当k1=k2=…=km=k,从而λ1=λ2=…=λm=λ时,{A1,A2,…,Am}为(n,m;k,λ)-EDF,当且仅当(S,G,E)为R-最优的弱AMD码.

而G-最优的弱AMD码和强AMD码相当于BoundedGSEDF这类组合设计,这里从略,可参见文献[6].

基于上述应用,近年来人们对于EDF、GEDF、GSEDF这几种组合设计的构造方法和存在性问题做出了一系列研究,下面将综述这方面的进展和一些待研究的问题.

3 设计的构作和存在性问题

Cλ=θλC, 0≤λ≤e-1,C0=C, |Cλ|=f,

叫作是有限域Fq的e阶分圆类,当λ≡λ′(mode)时,Cλ=Cλ′.

定义 3.1 对于0≤i,j≤e-1.以(i,j)e表示方程x-y=1,x∈Ci,y∈Cj的解数,即(i,j)e=|(Cj+1)∩Ci|,叫作是Fq上的e阶分圆数.当i≡i′,j≡j′(modee)时,(i′,j′)e=(i,j)e.

下面列出分圆数的基本性质,多数性质可由分圆数的定义直接推出,详见文献[17].

引理 3.2 设q-1=ef,(i,j)=(i,j)e为Fq上的e阶分圆数.Cλ(0≤λ≤e-1)为Fq中的e阶分圆类,则对于0≤i,j≤e-1.

3) (i,j)=(-i,j-i).

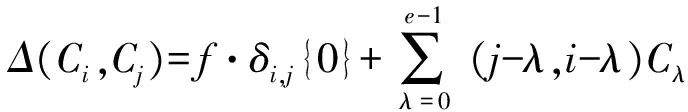
分圆数可以用数论中一批重要的特征和(雅可比和、高斯和)来表示,从而分圆数的计算依赖于数论中这些特征和的计算问题,这是数论本身的一个重要课题.目前对于e=2,3,4,5,6,…等小值,人们计算出e阶分圆数的值(可见文献[17]).这里只举一个简单情形作为例子.

例 3.1 设q=pr,p为奇素数,e=2,q-1=2f,则Fq上的2阶分圆数(i,j)=(i,j)2(0≤i,j≤1)为

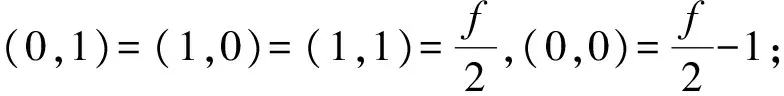
由引理3.2的5),当q≡3(mod4)时,

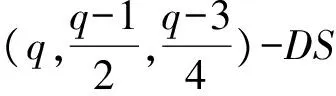
当q≡1(mod4)时,

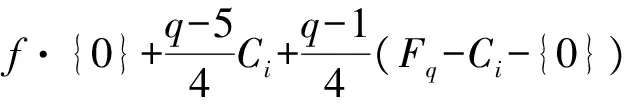
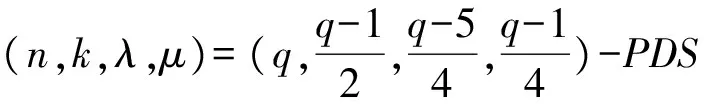
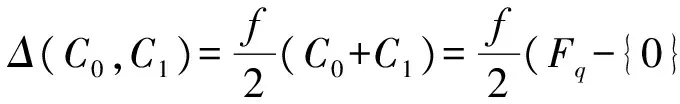
3.2 EDF的构造 在EDF的构作方面,分圆方法的起点是下面的结果.

定理 3.3 设q为素数幂,q-1=ef,Cλ(0≤λ≤e-1)为Fq中的e阶分圆类,则{C0,C1,…,Ce-1}为群(Fq,+)中(n,m;k,λ)=(q,e;f,q-f-1)-EDF.

证明 由引理3.2的5)有(记(i,j)=(i,j)e)

于是

Δ(Fq-{0},Fq-{0})-

(q-f-1)(Fq-{0}).

证毕.

进一步,可以取Ai(1≤i≤m)为e阶分圆类的一部分,也可取Ai为某些e阶分圆类之并集.在某些条件下,也可得到{A1,A2,…,Am}为(Fq,+)的GEDF和EDF,并且有更灵活的参数，参见文献[4，12，14，18].

除了分圆方法之外,构作EDF还有利用完全非线性函数[10],以及其它组合方法[11,14].

3.3 SEDF的构造 强外差组(SEDF)和它的推广:广义强外差组(GSEDF)是2016年提出的组合设计[6].至今只有为数不多的工作[19-23].GSEDF的构作基于以下2个结果.首先在文献[6]中证明了以下结果.

定理 3.4(文献[6]的定理2.4) 设A1,A2,…,Am(m≥2)是交换群(G,+)的分拆(即A1,A2,…,Am彼此不相交,其并集为G)，则{A1,A2,…,Am}为G中的(n,m;k1,k2,…,km;λ1,λ2,…,λm)-GSEDF,当且仅当每个Ai均为G中的(n,ki,ki-λi)-DS(差集合).

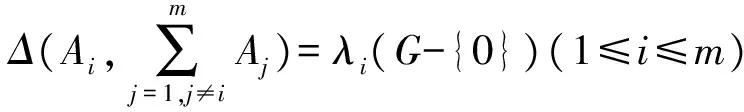
证毕.

熟知若A为G中的(n,k,λ)-DS,则它的补集合G-A为G中的(n,n-k,n-2k+λ)-DS.于是由定理3.4得到m=2的GSEDF.

系 3.5 设A为G中的(n,k,λ)-DS,则{A,G-A}为G的(n,2;k,n-k;k-λ,k-λ)-GSEDF.

类似于定理3.4,在文献[23]中证明了如下结果.

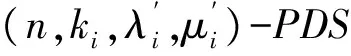
熟知若A∈G,0∉A,A为G的(n,k,λ,μ)-PDS,则当-A=A时A′=G-A-{0}为G的(n,n-k-1,λ′,μ′)-PDS,其中,λ′=n-2k+μ-2,μ′=n-2k+λ.若λ=μ-1,则λ′=μ′-1.于是定理3.6给出:

系 3.7(文献[23]的引理2.5) 设(G,+)为n阶交换群,A为G中的(n,k,λ,μ)-PDS,0∉A,-A=A,则{A,G-A-{0}}为G的(n,2;k,n-k-1;k-λ-1,k-λ-1)-GSEDF.

例 3.2 设q-1=2f,C0,C1为Fq的2阶分圆类.

对于e=2,4,6,8,文献[17]中已计算出有限域上的e阶分圆数,从而对某些e阶分圆类,Cλ或Cλ+{0}为Fq的差集合,由此因定理3.4可以构作Fq中的一些GEDF[19,20,23].另一方面,满足λ=μ-1的(n,k,λ,μ)-PDS是很少的.因为文献[24](还可见文献[25]的定理13.1)中证明了,若D为有限交换群G的(n,k;λ,μ)-PDS,λ=μ-1并且0∈D,D=-D,则参数必然为

(II) (n,k,λ,μ)=(243,22,1,2).

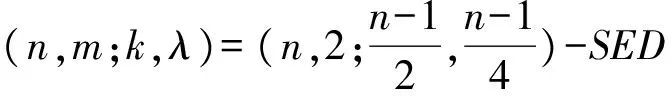
另一方面,构作m≥3的SEDF似乎是困难的,文献[6]中提出一个公开问题:是否存在m≥3的SEDF?不久文献[17]中证明了不存在m=3和m=4的SEDF,文献[19-20]又给出进一步的不存在性结果,但是当m≥5时是否存在SEDF一直是这些工作中不断提出的公开问题.

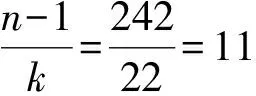
[1] 万哲先. 设计理论[M]. 北京:高等教育出版社,2009.

[2]LEVENSHTEINVI.Onemethodofconstructingquasilinearcodesprovidingsynchronizationinthepresenceoferrors[J].ProbInformTransm,1971,7:215-222.

[3]OGATAW,KURSAWAK,STINSONDR,etal.Newcombinatorialdisignsandtheirapplicationstoauthenticationcodesandsecretsharingshemes[J].DiscreteMath,2004,279(1):383-405.

[4]CHANGY,DINGC.Constructionsofexternaldifferencefamiliesanddisjointdifferencefamilies[J].DesCodesCryptogr,2006,40(2):167-185.

[5]CRAMERR,DODISY,FEHRS,etal.Detectionofalgebraicmanipulationwithapplicationstorobustsecretsharingandfuzzyextractors[J].LectureNotesinComputSci,2008,4965:471-488.

[6]PATERSONMB,STINSONDR.Combinatorialcharacterizationsofalgebraicmanipulationdectectioncodesinvolvinggeneralizeddifferencefamilies[J].DiscreteMath,2016,339(12):2891-2906.

[7]TONCHEVVD.Partitionsofdifferncesetsandcodesynchronization[J].FiniteFieldsandTheirAppl,2005,11(3):601-621.

[8]CRAMERR,FEHRS,PADROC.Algebraicmanipulationdetectioncodes[J].SciChinaMath,2013,56(7):1349-1458.

[9]DAVISJA,HUCZYNSKAS,MULLENGL.Near-completeexternaldifferencefamilies[J].DesCodesCryptogr,doi:10.1007/s10623-016-0275-7,2016.

[10]DINGC.Optimalandperfectdiffencesystemsofsets[J].JCombinTheory,2009,A116(1):109-119.

[11]FANCL,LEIJG,SHANXL.Constructionsofoptimaldifferencesystemsofsets[J].SciChinaMath,2011,54(1):173-184.

[12]FUJIWARAY,MOMIHARAK,YAMADAM.PerfectdifferencesystemsofsetsandJacobisums[J].DiscreteMath,2009,309(12):3954-3961.

[13]FUJIWARAY,TONCHEVV.D.Highrateself-synchronizingcodes[J].IEEETransInformTheory,2013,59(4):2328-2335.

[14]HUANGB,WUD.Cyclotomicconstructionsofexternaldifferencefamiliesanddisjointdifferencefamilies[J].JCombinDes,2009,17(4):334-341.

[15]LEIJ,FANC.Optimaldifferencesystemsofsetsandpartition-typecyclicdifferencepackings[J].DesCodesCryptogr,2011,58(2):135-153.

[16]NGSL,PATERSONMB.Disjointdifferencefamiliesandtheirapplications[J].DesCodesCryptogr,2016,78(1):103-127.

[17]STORERT.CyclotomyandDifferenceSets[M].Chicago:MarkhamPubCo,1967.

[18]MUTOHY,TOCHEVV.Differencesystemsofsetsandcyclotomy[J].DiscreteMath,2008,308(14):2959-2969.

[19]BAOJ,JIL,WEIR,etal.Newexistenceandnonexistenceresultsforstrongexternaldifferencefamilies[J/OL].arXiv:1612.08385,2016.

[20]HUCZYNSKAS,PATERSONMB.Existenceandnon-existenceresultsforstrongexternaldifferencfamilies[J/OL].arXiv:1611.05652,2016.

[21]MARTINW,STINSOND.Somenonexistenceresultsforstrongexternaldifferencefamiliesusingcharactertheory[J/OL].arXiv:1601.06432,2016.

[22]WENJ,YANGM,FENGK.The(n,m,k,λ)-strongexternaldifferencefamilywithm≥5exists[J/OL].arXiv:1612.09495,2017.

[23]WENJ,YANGM,FENGK.Cyclotomicconstructionofstrongexternaldifferencefamiliesinfinitefields[J/OL].arXiv:1701.01796,2017.

[24]ARASUKT,JUNGNICKELD,MASL,etal.StrongCayleygraphswithλ-μ=-1[J].JCombinTheory,1994,67(1):116-125.

[25]MASL.Asurveyofpartialdifferencesets[J].DesCodesCryptogr,1994,4(4):221-261.

[26]LEUNGKH,MASL.PartialdifferencesetsandPaleyparameters[J].BullLondMathSoc,1995,27(6):553-564.

[27]POLHILLJ.Paleypartialdifferencesetsingroupsofordern4and9n4foranyoddn > 1[J].JCobminTheory,2010,A117(8):1027-1036.

[28]JEDWABJ,LIS.Constructionandnonexistenceofstrongexternaldifferencefamilies[J].Preprint,2017.

2010 MSC：94B05

(编辑 李德华)

External Difference Families and Their Applications in Communication

YANG Minghui1, WEN Jiejing2, FENG Keqin3

( 1.StateKeyLaboratoryofInformationSecurity,InstituteofInformationEngineering,ChineseAcademyofSciences,Beijing100193; 2.ChernInstituteofMathematics,NankaiUniversity,Tianjin300071; 3.DepartmentofMathematicalScience,TsinghuaUniversity,Beijing10084)

Combinatorial designs have wide applications in communications. This paper is a survey on several new types of combinatorial designs including external difference family and its generalizations and variations, raised recently based on their applications in synchronization communication, authentication, secrete sharing schemes, etc. In this paper we explain the relationship between the new types of combinatorial designs and communication applications, introduce several construction method and existence results of these combinatorial designs and some unsolved problems.

difference set; generalized external difference family(GEDF); AMD code; authentication code; cyclotomic class; cyclotomic number

2017-03-02

国家自然科学基金(11571007和11471178)

O157.2

A

1001-8395(2017)04-0561-08

10.3969/j.issn.1001-8395.2017.04.021

*通信作者简介:冯克勤(1941—),男,教授,主要从事代数、数论和编码密码学理论的研究,E-mail:kfeng@math.tsinghua.edu.cn