椭圆凸轮波发生器零侧隙谐波齿轮传动共轭齿廓精确求解

杨勇，王家序, 2，周青华，祝晋旋，杨万友



椭圆凸轮波发生器零侧隙谐波齿轮传动共轭齿廓精确求解

杨勇1，王家序1, 2，周青华1，祝晋旋1，杨万友1

(1. 四川大学 空天科学与工程学院，四川 成都，610065；2. 重庆大学 机械传动国家重点实验室，重庆，400044)

提出一种凸轮波发生器谐波传动共轭齿廓精确求解法，该方法在求解过程中不作近似处理，并以原始曲线呈椭圆为例演示该算法求解共轭齿廓的过程。对双圆弧齿廓谐波传动共轭区间和共轭齿廓进行计算比较，结合有限元分析，验证算法的正确性和合理性。通过对不同算法求得的2组谐波传动分别求出侧隙分布和运用限元分析求得应力分布。研究结果表明：本文算法所得侧隙分布较近似算法更加微小均匀，并且由本文解法所得传动应力分布状况更优。

谐波齿轮；双圆弧齿廓；共轭；精确算法；椭圆

谐波齿轮传动因结构紧凑、质量轻、体积小而减速比大、传动精度高等诸多优点，广泛运用于航空航天和工业机器人等特殊领域。为了提高其传动性能，国内外学者对其运动学和啮合理论[1−6]、振动与动态性能[7−8]、齿廓形状[9−11]、位置精度[12−13]等领域开展了大量研究。随着空间机器人和航天飞行器的快速发展，对谐波减速器的性能，尤其是对体积、质量和传动精度等指标提出了更加严格的要求。谐波齿轮传动在波发生器作用下柔轮产生的周期性弹性变形是获得大变速比的前提，而且这种弹性变形决定着两轮轮齿共轭运动的规律。为获得更优的啮合性能和传动精度，对谐波传动中柔轮的变形进行深入研究，建立更精确的齿廓共轭算法实现零侧隙传动尤为必要。谐波减速器在装配后柔轮产生变形，柔轮轮齿的位置变化除径向位移和切向位移外，其对称线还相对于矢径旋转了一个角度。在用包络理论和运动学法求谐波齿轮传动共轭齿廓的方法中，为了计算方便，对柔轮轮齿对称线相对于矢径的转角和柔轮中线变形的切向位移引起的转角都采用近似方法求解。DONG等[4]提出了平面谐波传动运动学原理，为建立更精确的共轭方程提供了理论基础。陈晓霞等[6]提出了基于柔轮弹性变形的包络理论精确算法，提高了共轭齿廓求解精度，但仍可完善。本文作者参考现有柔轮弹性变形的多种分析和求解方法[1−6]，在假设1) 理想轻载，假设2) 柔轮中线变形前后不伸长，假设3) 柔轮轮齿相对柔轮齿槽为刚体，假设4) 变形后柔轮紧密贴合波发生器等的基础上，提出一种基于柔轮弹性变形和运动学的共轭精确算法。在轮齿啮合端，精确计算椭圆弧长、柔轮轮齿对称线相对于矢径的转角、柔轮中线变形切向位移引起的转角等各个参数，建立啮合方程，并利用数值法计算变形后柔轮齿的共轭齿廓，为零侧隙谐波齿轮传动共轭齿廓的求解和优化提供指导。

1 建立坐标系统及确定自变量

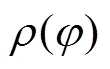
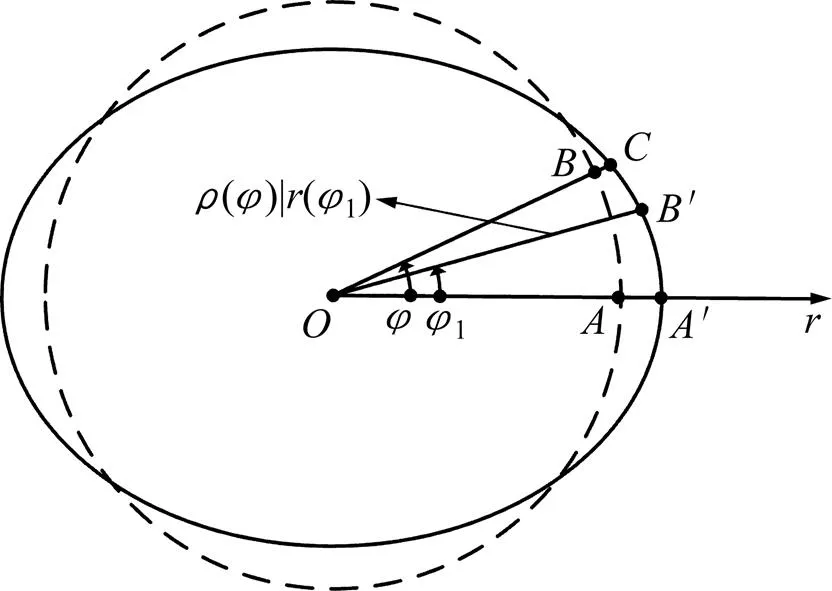
图1 极坐标中柔轮中性线变形前后

在极坐标系中平面曲线的弧长计算公式如下

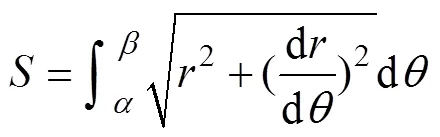
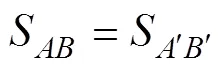
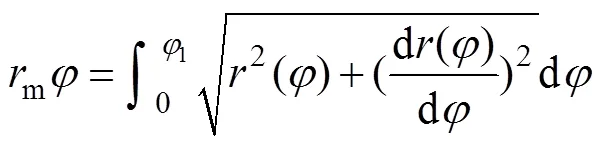
而不应是现在近似方法普遍运用的

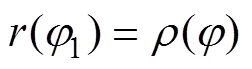
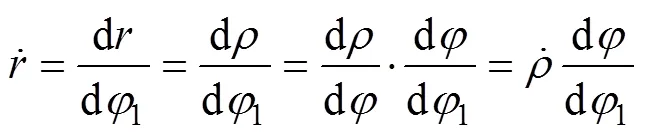
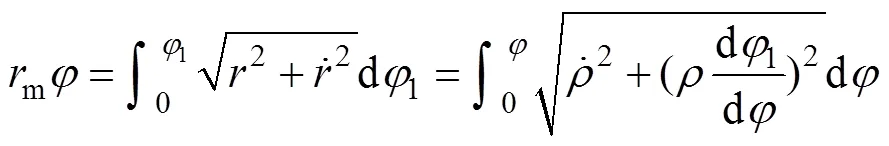
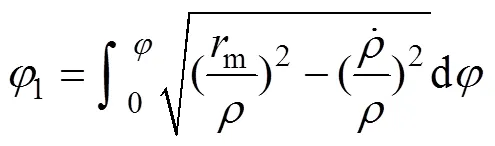
因此，求解谐波传动共轭齿廓可以考虑使用以上推导的精确表达式，或对所有运动参数选择以1(而不是)为自变量表示进行求解，1为以波发生器长轴为极轴的极坐标系的极角。本文算法取1为自变量表示所有运动参数，可精确简便地求解椭圆波发生器双圆弧齿廓谐波传动共轭齿廓。

建立如图2所示的坐标系统，用于描述柔轮、刚轮和波发生器之间的相对运动以及柔轮中线变形曲线上选定点的位移。假设刚轮固定，波发生器逆时针旋转输入，柔轮顺时针旋转输出。其中固定坐标系2{2，2，2}与刚轮相固连，2轴与刚轮齿槽对称线重合，原点2位于刚轮回转中心。动坐标系{，，}和1{1，1，1}分别与波发生器和柔轮啮合端轮齿相固连，轴与波发生器的长轴重合，原点位于波发生器的回转中心；1轴与柔轮轮齿对称线重合，原点1位于柔轮中线上。

柔轮中线变形曲线的位移示意如图2所示。初始位置是：1，2和三轴共线，坐标系，2重合，坐标系1中1点位于波发生器长轴顶点。图中所示位置为波发生器相对于2轴逆时针旋转2时，柔轮非变形端相对于2轴顺时针旋转，而变形端则顺时针旋转。根据谐波传动摩擦模型的运动学理论可知，传动时刚轮节圆和柔轮弹性节曲线是作纯滚动[1, 4]。因此刚轮相对波发生器旋转的角度2和柔轮相对波发生器旋转的角度1之间有如下关系：

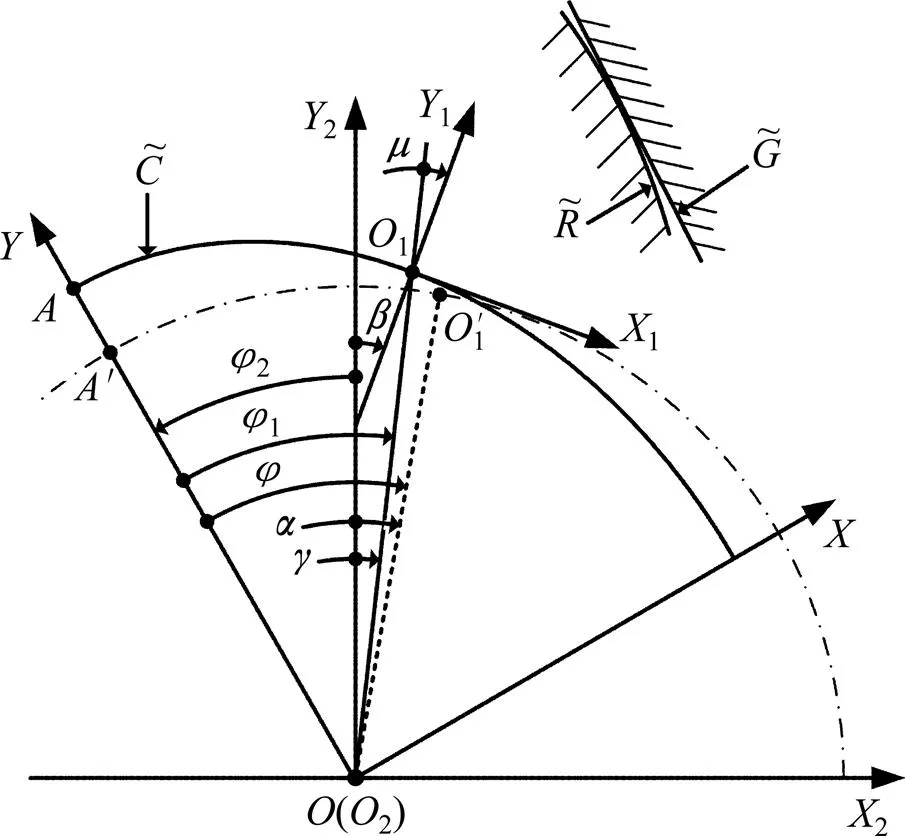
图2 谐波传动坐标系统

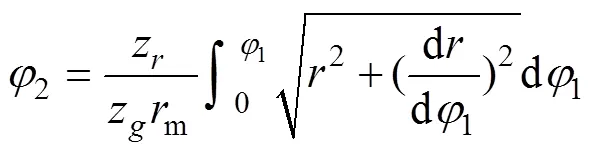
柔轮中线变形曲线由波发生器的形状决定，变形曲线的自变量为柔轮未变形端相对于波发生器长轴所旋转的角度，以图2所示顺时针为正。对图中转角变量，取方向与箭头方向一致为正值，否则为负值。波发生器迫使柔轮啮合端中线发生变形，使得1点从1处移动到图示1处，而且法线由1方向变为1方向。

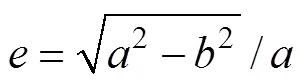
极径1的长度表达式如下

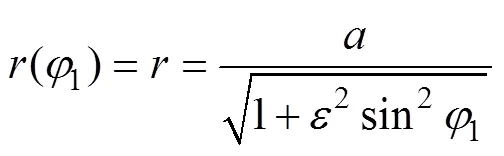
对式(7)求导可得

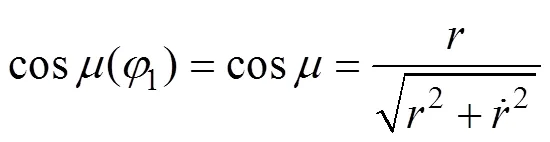
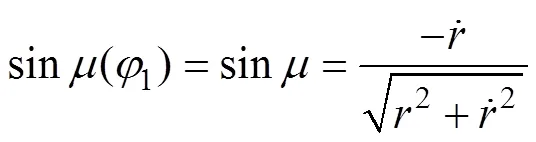
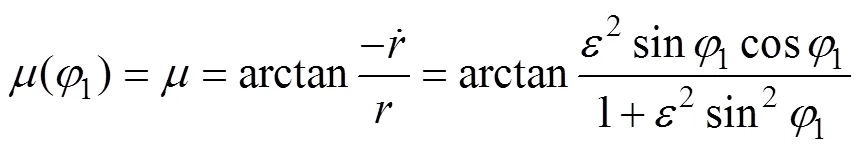
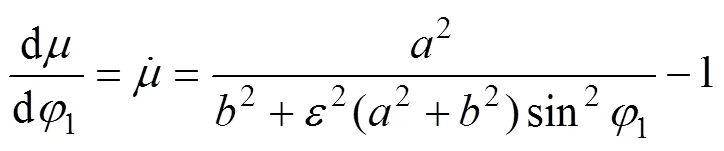
基于谐波传动中柔轮变形前后其中线不伸长的假设，可由下式确定

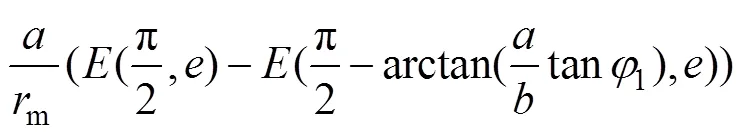
图2中其他角度也都能写成关于1的函数：

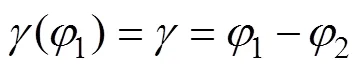
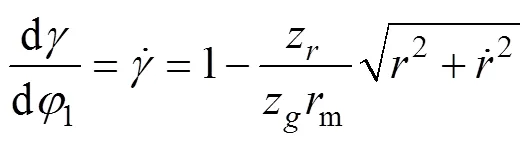
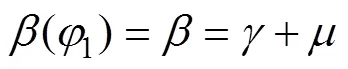
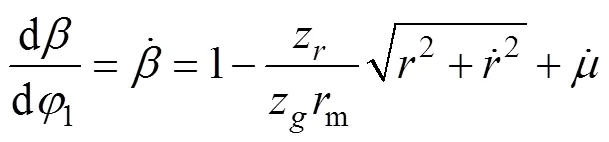
2 传统算法中的近似处理

在求谐波传动共轭齿形的传统包络法[1]中，以柔轮未变形端转角为自变量，表示出矢径()、径向变形()、周向变形()和转角变形()等变量，再作一些简化计算的近似处理来求解。主要存在以下近似处理。

2.1 变形后柔轮中性层变形曲线转角

为求得变形后柔轮中性层变形曲线转角1，传统算法还需对式(2)做如下近似处理[6]，否则不能解析表达。

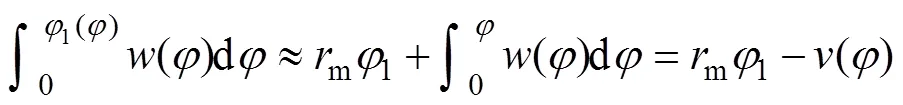
由此可将1表示成自变量的函数，即

而在本文算法中，以1为自变量，式(13)不仅能够精确表示，还可以方便地运用数学软件进行处理和计算。

2.2 齿廓对称线相对于径矢的转角

对于柔轮轮齿对称线相对于径矢转过角度，为便于计算进行了以下近似处理[1]。

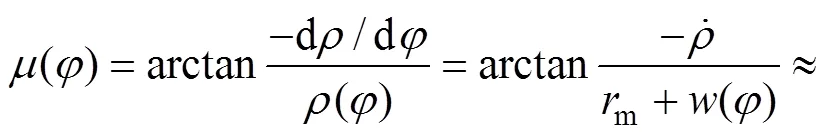
因为不会增加太多计算困难，所以本文算法对没有进行近似处理；文献[6]中虽然也没有采用近似处理，但需由1用复杂的定积分表示，大大增加了计算难度。

3 求解共轭齿廓的精确算法

图2中坐标系1到2的坐标变换矩阵21和底矢变换矩阵21分别如下：

1.2 现代中医研究 现代中医对小儿厌食症也多有研究，赵琼等[3]分析认为本病证型以脾胃气虚、脾虚食积、脾胃阴虚、脾虚湿困、肝脾不调为主。温爱平等[4]研究显示，小儿厌食病因为饮食不节、多病久病、暑湿熏蒸、先天不足，其中饮食不节占53.1%。胡爱国[5]对300例厌食症患儿进行病因分析，发现饮食不节、喂养不当者占47.9%，多病久病、伤害脾胃者占27.1%，先天不足、后天失调者占20.8%，暑湿熏蒸、脾阳失展者占3.3%，环境变化，思虑伤脾者占0.8%。闫雁等[6]则认为小儿厌食尚有肝脾郁结、肝阴虚、肝胆湿热证型，故从肝论治本病能取得较好疗效。

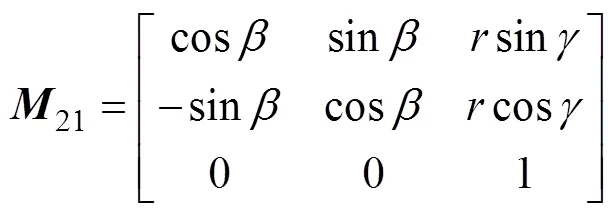
根据运动学法，在相互包络齿廓的接触点处，相对运动的速度矢量应当垂直于齿廓的法线矢量，即两曲面在接触点处必须满足以下啮合方程[15]

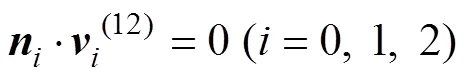
式中：和(12)分别表示在坐标系S中两共轭曲面在接触点处的公法矢和相对速度矢。

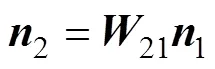
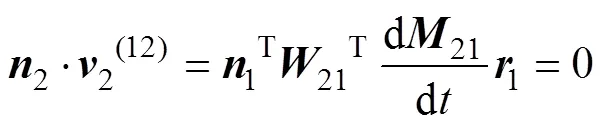
定义矩阵，令

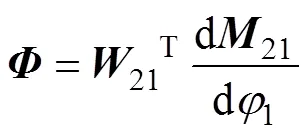
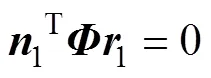
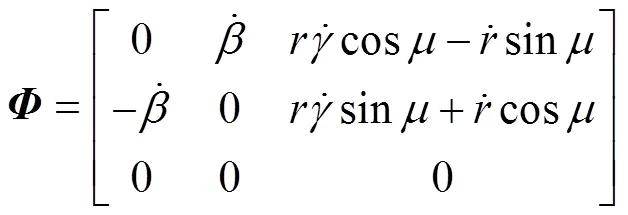
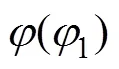
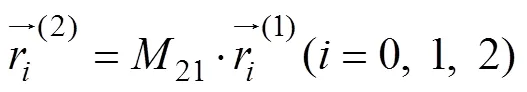
4 计算实例

以波发生器为标准椭圆凸轮的双圆弧谐波齿轮传动为例，柔轮轮齿局部坐标系和公切线式双圆弧齿廓如图3所示。

选取模数0.317 5 mm，径向变形系数0=1.0，全齿高=1.5 m，齿顶高a=0.6 m，齿根高f=0.9 m，柔轮齿数z=160，刚轮齿数z=162，具体参数见表1。

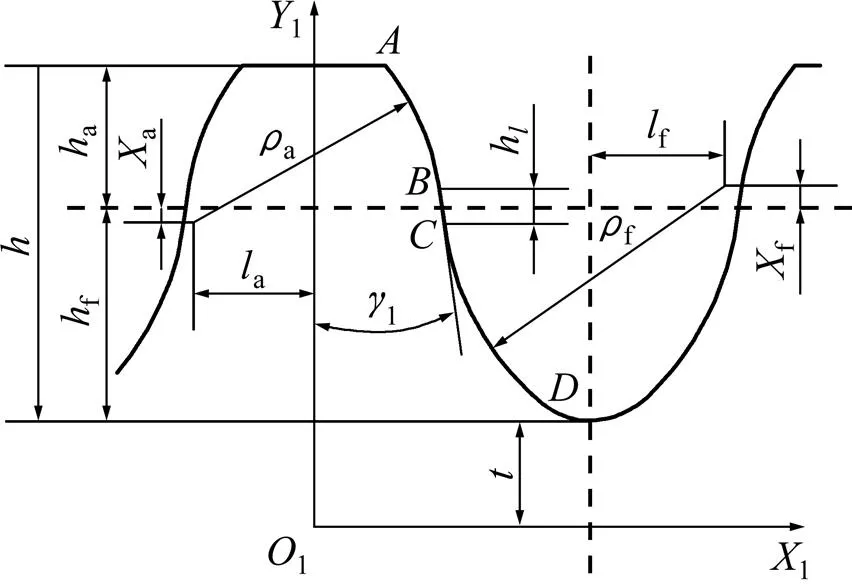
图3 双圆弧齿廓及柔轮轮齿坐标系

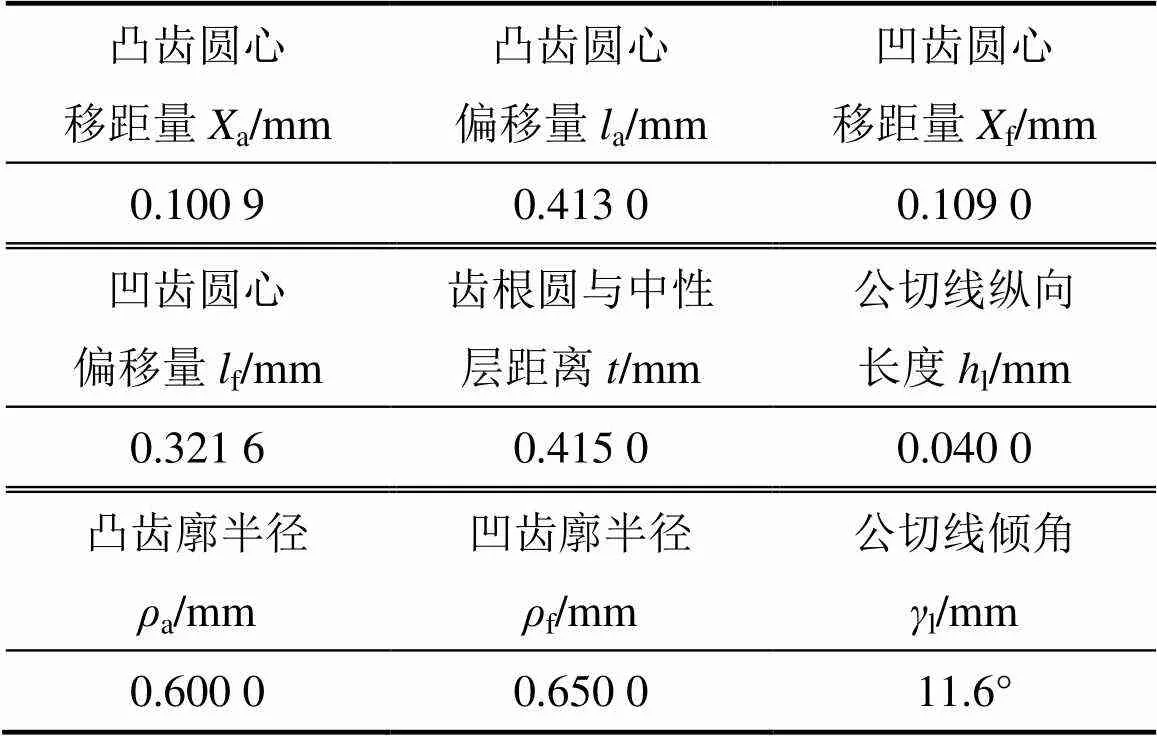
表1 柔轮齿廓参数

4.1 所得共轭离散点比较

分别采用近似算法和本文所提的精确算法求得此谐波传动柔轮的共轭区间和共轭齿廓，如图4和图5所示。

从图4可看出：由不同算法求得柔轮齿廓上各个点发生共轭时对应的有明显差异，且在共轭Ⅰ区两者的差别较共轭Ⅱ区更加显著(齿廓的先、后2次共轭区域，分别称为共轭Ⅰ区和Ⅱ区[17])。在共轭Ⅰ区靠近齿顶或齿根处差异要小于中间部分，差异由中间向两端逐渐减小；而在共轭Ⅱ区除凸圆弧齿廓和直线段齿廓相切点附近差别明显较大外，其他地方差异则较为均匀。采用本文算法得出的齿廓共轭区域Ⅰ和Ⅱ之间的距离更近，总共轭区间明显大于近似算法的总共轭区间，将使参与啮合的齿对处于共轭啮合而不是尖点啮合的数目更多，对提高双圆弧谐波齿轮传动精度和扭转刚度有重要意义。

本例谐波传动存在2次共轭现象，由本文算法求得的第1次共轭区间为[2.912 307°，10.880 029°]，第2次共轭区间为[12.493 927°，46.968 601°]；而由近似算法求得的第1次和第2次共轭区间分别为 [2.549 667°，7.786 985°]与[13.652 177°，46.018 008°]。第1次和第2次共轭区间最小角度偏移量分别为0.362 640°和1.158 250°，最大角度偏移量为3.093 045°和0.950 593°。定义偏移角度与共轭区间大小之比为偏差[6]，则在第1次共轭区间内最大值偏差为38.82%，最小值偏差为4.55%；在第2次共轭区间内最大值偏差为2.76%，最小值偏差为3.36%。

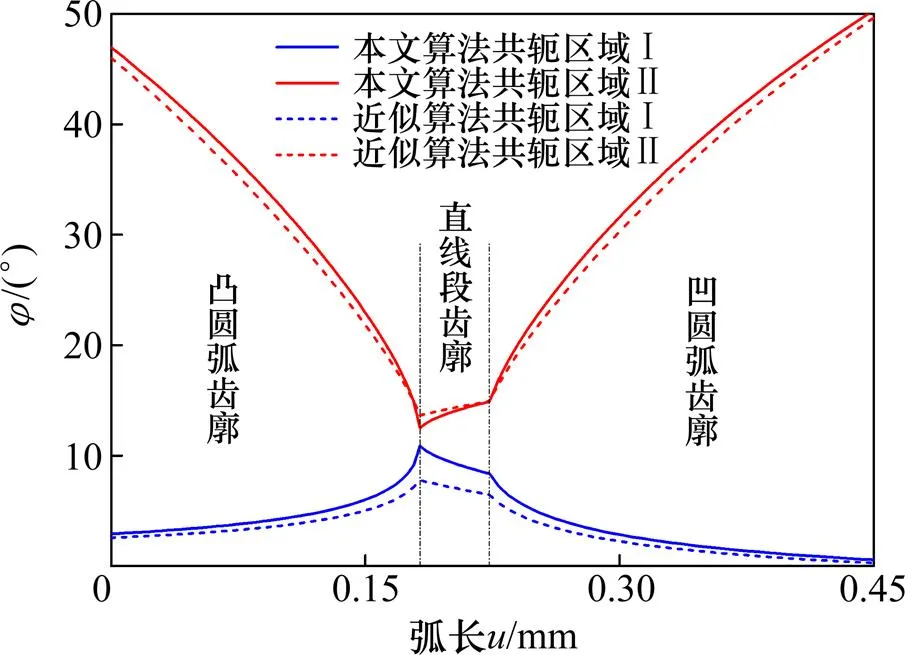
图4 柔轮齿廓共轭区间比较

图5所示为不同算法对求取刚轮的理论共轭齿廓的影响。由图5可知：算法差异对共轭凹齿廓的影响很小，而对共轭凸齿廓的影响更明显。因为谐波齿轮齿廓精细，细微的变化可能明显改善性能，特别是对轮齿侧隙影响显著(因侧隙为微米级)，所以不容忽视。

(a) 凹齿廓；(b) 凸齿廓

4.2 圆弧拟合后比较

本例中柔轮齿廓参数是经过文献[17]提出的齿廓优化方法得出的优化值，存在一定“双共轭区”，易于实现谐波齿轮的零侧隙传动。为便于加工制造和量化分析，对分别由2种算法求得的柔轮共轭齿廓离散点进行圆弧拟合，得到各自对应的刚轮齿廓，其相关参数见表2。

表2 刚轮齿廓参数对比

从表2可看出：2种算法求得的齿廓各个参数的差别在10−2 mm的量级上，而且算法的不同对刚轮凸齿廓的影响较凹齿廓更明显。定义齿廓半径差与半径之比为偏差，则凹齿廓半径偏差为1.72%，凸齿廓半径偏差为8.50%。

为直观地反映装配变形后双圆弧谐波齿轮的啮合状态及侧隙分布，通过不断改变波发生器转角，对柔轮齿廓坐标进行坐标变换来模拟柔轮和刚轮轮齿的相对运动状态。在波发生器旋转取0°~90°，基于本文提出共轭算法的柔轮轮齿相对于刚轮齿槽的运动轨迹如图6所示。由图6可知：啮合过程中柔轮与刚轮齿廓未发生干涉。

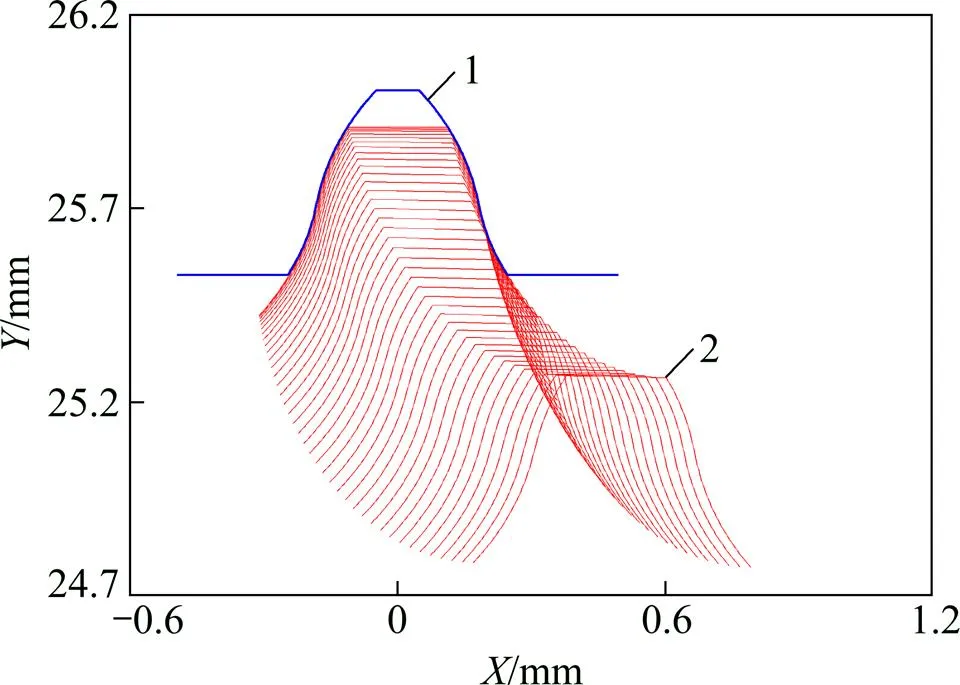
1—刚轮齿廓；2—柔轮齿廓。

此例中波发生器单侧啮合齿对为23对，运用文献[18]提出的侧隙求解方法，基于MATLAB设计程序计算各齿对侧隙。在椭圆凸轮波发生器作用下，由不同算法求得的2组齿轮副之间的侧隙分布如图7所示，图中，横坐标表示齿数，将波发生器长轴对应的柔轮轮齿记为0，往右侧数依次记为1，2，3，…，，往左侧方向的齿则记为负数；纵坐标表示侧隙，对已发生齿廓重叠干涉的齿对侧隙用负数表示，经验证均没有干涉发生。从图7可看出：根据本文算法求得的齿轮副齿对之间侧隙分布均匀，右侧各个齿对整体上侧隙在0.2 μm左右，最大值为0.316 4 μm对应横坐标为1，最小值为0.052 4 μm；而近似算法右侧各齿对间侧隙分布不够均匀。虽然2组齿廓侧隙都很小，但根据本文算法求得的齿轮副齿对间侧隙分布较近似算法波动性更小、更均匀，在动力传递中有利于合理分配齿间载荷，减小振动冲击，提高承载能力和传动性能。

1—本文算法；2—近似算法。

4.3 有限元分析

考虑到传动时没有轴向力，也没有限制轴向应变的约束，因而没有轴向应力，采用平面应力有限元模型是合理的[9]。谐波齿轮传动由刚轮、柔轮和波发生器组成，波发生器带有滚珠轴承外圈呈椭圆，当波发生器装入柔轮内，柔轮内圈将与波发生器外圈相贴合而呈椭圆，在有限元模型中可略去滚珠轴承把波发生器简化成椭圆形的刚体[11]。按照本例双圆弧谐波传动所求参数，在UGNX中建立三维模型，提取二维特征后以Parasolid格式导入非线性有限元分析软件ABAQUES进行平面有限元分析。柔轮材料为30CrMnSiNiA，弹性模量为206 GPa，刚轮材料为45钢，弹性模量为210 GPa，泊松比为0.3，密度为7.8×103kg/m3。

因可能涉及到非常大的网格扭曲问题，采用细网格剖分的线性减缩积分单元CPS4R对谐波传动各组件进行结构化网格划分，并对装配和传动过程中参与啮合计算的轮齿齿侧及齿根处的网格适当加密网格大小为0.02 mm。在整个有限元模型中上下半椭圆凸轮分别划分为2 180个CPS4R单元，环形柔轮被划分成176 114个CPS4R单元，刚轮被划分成146 379个CPS4R单元和4 111个CPS3单元。装配后网格划分情况如图8所示。采用动力显式模块Explicit进行准静态分析，模拟波发生器装配入柔轮的过程。由于在波发生器装入前，柔轮体是圆形的，而波发生器是椭圆，其长轴要比柔轮体内圆半径大，因此在对谐波齿轮进行模拟装配时，先将波发生器分成2个半椭圆，2个半椭圆分别向内缩进径向变形量0=0.317 5 mm，分别指定好各自的参考点，模拟时把上下2个半椭圆视为刚体，在定义边界条件时给定上半凸轮参考点向上的位移和下半凸轮参考点向下的位移，其值为0。由于柔轮被撑开后柔轮上某些区域可能变形量较大，属于大位移，所以在分析时，设置成非线性分析，分析完成后，2个参考点刚好在凸轮中心点重合，柔轮发生初始变形，形成初始应力，同时还可以看到柔轮，刚轮在装配后的初始啮合情况。接着类似普通齿轮副啮合静力分析方法，设置刚轮与柔轮之间的摩擦因数设为0.01，柔轮内壁固定，在刚轮回转中心上加载 20 N·m转矩，采用通用模块Standard求解，分析受力情况。

图8 谐波齿轮有限元模型网格划分

图9所示为二维谐波传动有限元分析结果。由图9可见：对于施加相等转矩二者呈现出不同的应力分布状态，最大应力相差近40%。本文算法所得的各接触齿对间受力较均匀，而由近似算法所得应力中有少部分接触齿对受力很小，对于啮入较深主要承受载荷的6对齿，本文算法所得的柔轮齿根应力比近似算法同位置的应力均小10 MPa，而本文算法所得的齿面应力比近似算法的均匀得多，本文算法所得为218，213，221，292，331和341 MPa；近似算法为205，188，322，412，522和481 MPa；而对于啮出部分，本文算法所得啮出齿对柔轮刚轮齿顶间隙比近似算法所得的大，出现齿顶干涉的可能性更低。综上可知，采用本文算法求得的刚轮齿廓与柔轮齿啮合时将具有更好的力学性能。

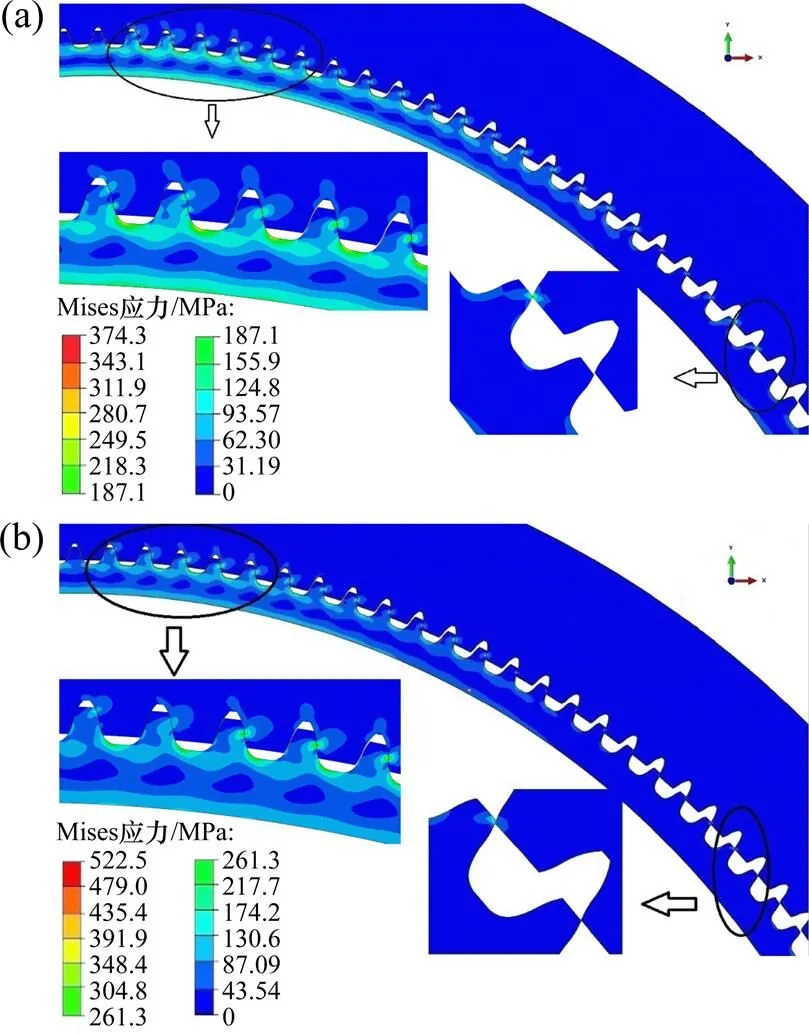
(a) 本文算法；(b) 近似算法

5 结论

1) 提出一种求解共轭齿廓的精确算法，可方便地求解计算，所得共轭点更可靠。

2) 从数学上，传统算法中表示柔轮变形前后对应弧长相等的等式两边不是精确相等而是近似相等，因而给出了精确表达式。

3) 本文算法求得的谐波传动侧隙要比近似算法求得的结果更为均匀合理，波动性更小，这对提高谐波传动承载能力和传动性能有重要意义。

4) 通过对实例进行有限元分析，得出采用本文算法求出的刚轮齿廓与柔轮啮合过程中将具有更佳的应力分布，也可降低发生齿顶干涉的可能。

5) 文中以原始曲线为椭圆的凸轮波发生器谐波齿轮传动为例介绍共轭齿廓精确求解法，但此方法的求解思想对原始曲线为(工程上有应用的)任意形状的谐波传齿轮动都适用。

[1] 沈允文, 叶庆泰. 谐波齿轮传动的理论和设计[M]. 北京: 机械工业出版社, 1985: 34−110, 370−386. SHEN Yunwen, YE Qingtai. Theory and design of harmonic gear transmission[M]. Beijing: China Machine Press, 1985: 34−110, 370−386.

[2] 辛洪兵. 研究谐波齿轮传动啮合原理的一种新方法[J]. 中国机械工程, 2002, 13(3): 181−183. XIN Hongbing. A new method for research on engagement principle of harmonic drive[J]. China Mechanical Engineering, 2002, 13(3): 181−183.

[3] 董慧敏. 基于柔轮变形函数的谐波齿轮传动运动几何学及其啮合性能研究[D]. 大连: 大连理工大学机械工程学院, 2008: 15−25. DONG Huimin. Study of kinematics and meshing characteristic of harmonic gear drives based on the deformation function of the flexspline[D]. Dalian: Dalian University of Technology. School of Mechanical Engineering, 2008: 15−25.

[4] DONG H M, TING K L, WANG D L. Kinematic fundamentals of planar harmonic drives[J]. Journal of Mechanical Design, 2011, 133(1): 011007.

[5] DONG H M, TING K L, WANG D L. Kinematic effect of the compliant cup in harmonic drives[J]. Journal of Mechanical Design, 2011, 133(1): 051004.

[6] 陈晓霞, 林树忠, 邢静忠. 谐波齿轮传动中基于柔轮装配变形的共轭精确算法[J]. 中国机械工程, 2010, 21(17): 2053−2057. CHEN Xiaoxia, LIN Shuzhong, XING Jingzhong. Exact conjugate algorithm based on assembly deformation of flexspline in harmonic drives[J]. China Mechanical Engineering, 2010, 21(17): 2053−2057.

[7] TUTTLE T D, SEERING W. Modeling a harmonic drive gear transmission[C]//Proceedings of 1993 IEEE International Conference on Robotics and Automation. New York: IEEE, 1993: 624−629.

[8] ZHANG Huibo, PAN B, WANG Long, et al. Non-linear dynamic modeling and experiment of harmonic gear drive[J]. Applied Mechanics & Materials, 2014, 668: 217−220.

[9] DENNIS L, NELSON A, ANDRE’S T. Statistical analysis of the influence of tooth geometry in the performance of a harmonic drive[J]. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 2015, 37: 723−735.

[10] ISHIKAWA S, KIYOSAWA Y. Flexing contact type gear drive of non-profile-shifted two-circular-arc composite tooth profile: United States, US 5458023[P]. 1995−10−17.

[11] OGUZ K, FEHMI E. Shape optimization of tooth profile of a flexspline for a harmonic drive by finite element modelling[J]. Materials and Design, 2007, 28: 441−447.

[12] GANDHI P S, GHORBEL F. High-speed precision tracking with harmonic drive systems using integral manifold control design[J]. International Journal of Control, 2005, 78(2): 112−121.

[13] ZHANG Hongwei, AHMAD S, LIU Guangjun. Torque estimation for robotic joint with harmonic drive transmission based on position measurements[J]. IEEE Transactions on Robotics, 2015, 31(2): 322−330.

[14] 过家春, 张庆国, 章林忠, 等. 基于第二类椭圆积分的椭圆弧长公式变换与应用[J]. 数学的实践与认识, 2011, 41(24): 210−216. GUO Jiachun, ZHANG Qingguo, ZHANG Linzhong, et al. Transformation formulas for the elliptic arc length and its application based on the elliptic integral of the second kind[J]. Mathematics in Practice and Theory, 2011, 41(24): 210−216.

[15] 李特文. 齿轮啮合原理[M]. 2版. 上海: 上海科学技术出版社, 1984: 33−80. LITVIN. Theory of gearing[M]. 2nd ed. Shanghai: Shanghai Science and Technology Press, 1984: 33−80.

[16] 张福润, 罗伯勋. 建立啮合方程的B矩阵法[J]. 华中理工大学学报, 1990, 18(2): 9−16. ZHANG Furun, LUO Baixun. The engaging equation by the B matrix method[J]. Journal of Huazhong University of Science and Technology, 1990, 18(2): 9−16.

[17] 杨勇, 王家序, 周青华, 等. 双圆弧谐波齿轮传动柔轮齿廓参数的优化设计[J]. 四川大学学报(工程科学版), 2016, 48(1): 186−193. YANG Yong, WANG Jiaxu, ZHOU Qinghua, et al. Optimization design for flexspline tooth profile parameters of double-circular-arc harmonic drives[J]. Journal of Sichuan University (Engineering Science Edition), 2016, 48(1): 186−193.

[18] CHEN Xiaoxia, LIU Yusheng, XING Jingzhong, et al. The parametric design of double-circular-arc tooth profile and its influence on the functional backlash of harmonic drive[J]. Mechanism and Machine Theory, 2014, 73(2): 1−24.

(编辑 赵俊)

Exact solution for conjugate profiles of zero backlash harmonic drives with elliptical cam wave generators

YANG Yong1, WANG Jiaxu1, 2, ZHOU Qinghua1, ZHU Jinxuan1, YANG Wanyou1

(1. School of Aeronautics and Astronautics, Sichuan University, Chengdu 610065, China; 2. State Key Laboratory of Mechanical Transmissions, Chongqing University, Chongqing 400044, China)

An exact solution for conjugate profiles of a harmonic drive (HD) with a cam wave generator was presented. The details of the precise solution without approximate treatments were demonstrated through solving the conjugated tooth profiles of a HD with an elliptical cam generator. The accuracy and effectiveness of the proposed solution were verified by comparative analyses of conjugate domains and conjugate tooth profiles of HDs with double-circular-arc tooth profile (DCTP). The differences between the backlash distributions derived by the two algorithms and the finite element analyses (FEA) of the HDs were obtained. The results reveal that smaller and more uniform backlash distributions and better distributions of stress are achieved with the proposed exact solution.

harmonic drive; double-circular-arc tooth profile; conjugate; exact solution; ellipse

10.11817/j.issn.1672−7207.2017.12.013

TH132.43

A

1672−7207(2017)12−3231−08

2016−12−12；

2017−03−18

国家高技术研究发展计划(863计划)项目(2015AA043001)；国家自然科学基金资助项目(51435001，51405316)；中航工业产学研专项(CXY2013CD36)(Project (2015AA043001) supported by the National High-Tech Research and Development Program (863 Program) of China; Projects (51435001, 51405316) supported by the National Natural Science Foundation of China; Project (CXY2013CD36) supported by the Industry University Research Projects of Aviation Industry Corporation of China)

周青华，博士，副教授，从事空间摩擦学与可靠性工程、多尺度飞行器机构设计与分析研究；E-mail：qh.zhou@foxmail.com