逻辑理论的随机相容度

李修清，张超权

桂林航天工业学院 理学部，广西 桂林 541004

1 引言

在计量逻辑学中，相容理论的相容度研究是关注较高的一个问题[1-3]。文献[4]在对二值逻辑系统随机化研究基础上对理论的相容度进行了研究，得出了理论相容度的基本定理。

本文在惠小静，李修清等对多值逻辑系统的随机化研究成果（见文献[4-12]）基础上，在n值Lukasiewicz命题逻辑系统中，提出理论的随机相容度概念，得出了在n值命题逻辑系统中，理论的随机相容度也保持了经典逻辑度量空间中理论相容度的基本性质。同时也指出了基于命题随机真度的理论的随机相容度和基于命题真度的理论的相容度是具有本质差异的。

2 随机真度、随机伪距离

本文未加说明的概念与符号，参见文献[13-15]。

设A=A(q1,q2,…,qm)∈F(S)是一个含m个原子公式的命题公式，则公式A自然对应一个m元函数如下 ：，将 A=A(q1,q2,…,qm)中 的 q1,q2,…,qm分 别 用α=(x1,x2,…,xm)中的x1,x2,…,xm替换，相应的公式 A中的联结词¬,∨,→也用Wn中的算子¬,∨,→替换，则得一个到Wn的m元函数：→Wn，称为公式 A诱导的函数，记作。显然，诱导函数关于运算¬,∨,→是同态的。

设p=(p1,p2,…)是一个n维概率分布列，其中p1=(p11,p21,…,pn1)T，p2=(p12,p22,…,pn2)T，… ，∀α=(x1,x2,…,xm)∈Wmn，令φp(α)=φ1(x1)×φ2(x2)×…×φm(xm)，定义为时，φ(x)=p(k=1,2,…,n;i=1,2,…,m)，iiki则得到一个Wmn到[0，1]区间的映射φp(α):Wmn→[0,1]，称为Wmn上的一个随机化映射。

关于随机化映射有以下结论。

命题2.1[10]设p=(p1,p2,…)是一个n维概率分布列，φp(α)为Wmn上的一个随机化映射，则

事实上，可以构造一个离散型随机变量ξ如下：ξ的所有可能取值为Wmn中的全部点Wmn，定义ξ取时的概率为 p(ξ=α)=φp(α)，则 由 命 题 2.1 可 得 ：且于是ξ就构成了一个离散型随机变量。即可看成一个取值为的某个离散型随机变量的分布律。

定义 2.1[6]设xm)是A的诱导函数，p=(p1,p2,…)是一个n维概率分布列，φp为Wmn上的随机化映射，令

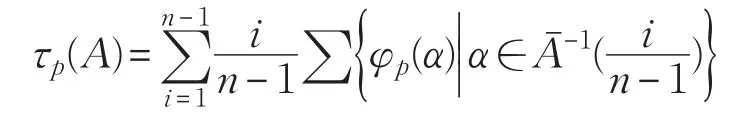
称τp(A)为公式A的随机真度。

关于随机真度还可以变形为一个更便于计算的公式。

命 题 2.2[12]设xm)是A的诱导函数，p=(p1,p2,…)为一n维概率分布列，φp为随机化映射，则

下文还要用到以下结论。

定理2.1设A,B∈F(S)，则以下各结论成立：

（1）设A是重言式，则对于任意的n维概率分布列p=(p1,p2,…)，都有τp(A)=1；反之未必成立。

（2）设A是矛盾式，则对于任意的n维概率分布列p=(p1,p2,…)，都有τp(A)=0；反之未必成立。

（3）若A≈B，则对于任意的n维概率分布列p=(p1,p2,…)，有τp(A)= τp(B)。

（4）对于任意的n维概率分布列 p=(p1,p2,…)，有τp(¬A)=1- τp(A)。

证明（1）设A含有m个原子公式q1,q2,…,qm，若A是重言式，则∀α=(x1,x2,…,xm)∈Wnm，恒有=1，设p=(p1,p2,…)是任取的n维随机概率分布列，φp为随机化映射，由命题2.2知：

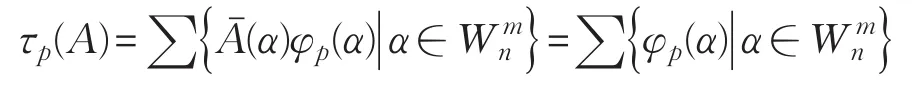
注意到命题2.1显然得τp(A)=1。反之若存在一个n维随机概率分布列，使τp(A)=1，构造一个n维随机概率分布序列 p=(p1,p2,…)如下：p1,p2,…,pm,…中的每一个n维概率分布pi均为第n个分量等于1，其余n-1个分量均为0，则对于这个n维随机概率分布序列，∀α=且α≠(1 ,1,…,1) 时，φp(α)=0，故由命题2.1易得：φp(1,1,…,1)=1。构造一个含m个原子公式的命题公式A=A(q1,q2,…,qm)，使得当时时均有Aˉ(α)=0，则显然命题公式A不是重言式，但根据命题2.2计算得这样将证明了（1）的结论。

（2）与（1）同理可证。

（3）运用命题2.2易证。

（4）运用命题2.1和命题2.2易证。证毕。

定理2.2[12]设A,B∈F(S)，p=(p1,p2,…)为一n维概率分布列，则以下各结论成立：

（1）τp(A∨B)=τp(A)+τp(B)-τp(A∧B)。

（2）τp(A→B)=τp(A∧B)-τp(A)+1。

（3）若A→B，则τp(A)≤τp(B)。

由随机真度的上述结果，可以引入命题公式间的随机伪距离概念，并建立随机逻辑度量空间。

定义2.2[12]设p=(p1,p2,…)是一n维概率分布列，A,B∈F(S)，令δp(A,B)=τp((A→B)∧(B→A))，称为公式A与B间的随机相似度。

由随机真度的定义显然有：δp(A,B)=δp(B,A)。

随机相似度，有以下结论。

定理2.3[12]设p=(p1,p2,…)为一n维概率分布列，A,B,C ∈ F(S)，则

（1）A≈B时有δp(A,B)=1。

（2）δp(A,B)+δp(B,C)≤1+δp(A,C)。

利用随机相似度概念，引入命题公式间的随机伪距离。

令ρp(A,B)=1-δp(A,B)，则由定理2.3易得ρp(A,B)+ρp(B,C)≥ρp(A,C)，且ρp(A,A)=0和ρp(A,B)=ρp(B,A)，所以ρp构成空间的距离，称为F(S)上的随机伪距离，这时称空间(F(S),ρp)为随机逻辑度量空间。

3 逻辑理论的随机相容度

全体命题公式集F(S)的任意一个子集Γ叫做F(S)的一个逻辑理论或理论。设Γ是F(S)的一个逻辑理论，如果从公式集Γ推不出矛盾式ˉ，则称逻辑理论Γ是相容的，否则称Γ是不相容的。

以D(Γ)表示Γ的全体结论之集，令

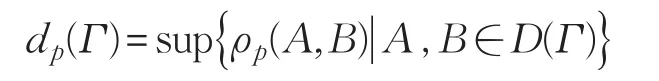
称为逻辑理论Γ的基于n维随机概率分布序列p的随机直径（有些文献也称为随机发散度[12]）。

由定义显然知，0≤dp(Γ)≤1。

首先证明对于不相容逻辑理论，无论基于怎样的n维随机概率分布序列，随机直径恒为1，即不相容逻辑理论的随机直径和随机概率分布序列p的取值没有关系。

定理3.1设Γ⊆F(S)是不相容逻辑理论，p是任取的一个n维随机概率分布序列，则有dp(Γ)=1。

证明设Γ是不相容的逻辑理论，则由文献[14]知，这时D(Γ)=F(S)，取T为定理为矛盾式，任取一个n维随机概率分布序列p，由命题间伪距离的定义显然有，，从而可得，无论对于怎样选取的n维随机概率分布序列p，Γ的随机直径dp(Γ)=1。证毕。

但该定理的逆命题是不正确的，即若存在一个n维随机概率分布序列p，使得某一理论Γ的随机直径dp(Γ)=1，也不能推出Γ就是不相容的逻辑理论。如：取Γ为全体原子公式集S，取n维随机概率分布序列p为均匀概率分布，则这时dp(S)=1（见文献[12]），但S是相容的逻辑理论[13]。

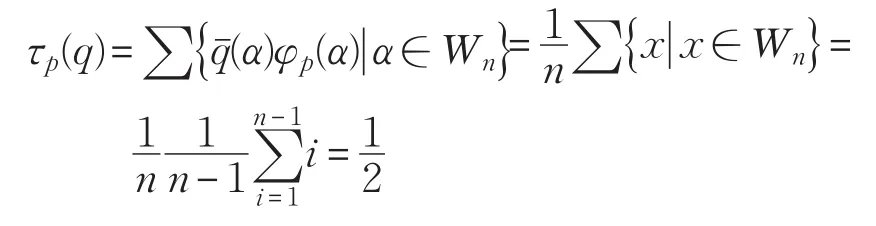
设Γ2中的公式全是定理，则设D(Γ2)是全体定理之集，则由伪距离的定义易知，Γ2基于均匀概率分布的n维概率分布列p的随机直径为0，即dp(Γ2)=0。

因此可见，相容理论的基于均匀概率分布的随机直径可以分布在[0,1]区间，这就和不相容理论基于任意概率分布列p的直径均为1大不相同，结果要复杂得多。

另一方面，同一个相容理论，其随机直径也和概率分布列p的选取有很大的关系。如文献[12]中的一个结论，取了一组适当的概率分布列p0，得出全体原子公式集S基于这一组取定p0的随机直径为dp0(S)=1-e-1。进一步对于任意一个实数0≤α≤1，是否都可以取到一组概率分布列p，使S基于这一组取定的概率分布列p的随机直径为α呢，这是值得进一步研究的问题。

由以上的讨论可以看出，相容理论的结构是很复杂的，尤其是相容理论的随机直径更是难以把握，相容理论和不相容理论的随机直径都可以是1，可见用随机直径刻画理论的相容度是有困难的，于是再加以细化，提出随机相容度的概念，并证明相容度的一些基本结论对于随机相容度概念同样成立。

首先给出随机极指标的概念：设Γ是F(S)的一个逻辑理论，D(Γ)是理论Γ的全体结论之集，p是任意一个n维概率分布列，令

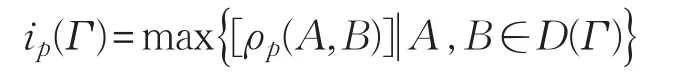
关于随机极指标易证。

定理3.2设Γ是F(S)的一个理论，对于任意一个n维概率分布列p，则Γ是相容理论当且仅当ip(Γ)=0，Γ是不相容理论当且仅当ip(Γ)=1。

证明设p是任取的一个n维概率分布列，因为[ρp(A,B)]=1当且仅当 ρp(A,B)=1，又因为 ρp(A,B)=1-τp((A→B)∧(B→A))，于是[ρp(A,B)]=1当且仅当τp((A→B)∧(B→A))=0，于是知命题A和B之间一个是重言式一个是矛盾式，所以由[ρp(A,B)]只能为1和0两个值知，ip(Γ)=1当且仅当Γ是不相容理论，Γ是相容理论当且仅当ip(Γ)≠1，从而只能有ip(Γ)=0。证毕。

下面给出随机相容度的概念。

定义3.1设Γ是F(S)的一个理论，p是任取的一个n维概率分布列，令

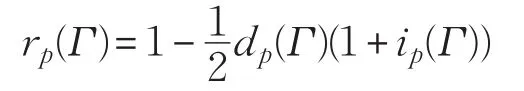
则称rp(Γ)为理论Γ基于概率分布列p的随机相容度。

关于随机相容度，有下面的基本结论。

定理3.3设Γ是F(S)的一个理论，p是任取的一个n维概率分布列，则

（1）Γ是不相容理论当且仅当对于任取的n维概率分布列 p，都有rp(Γ)=0。

（2）Γ是相容理论当且仅当对于任取的n维概率分布列p，都有，并且1和是可达的。

证明（1）设Γ是不相容的，则对于任取的n维概率分布列 p，由定理 3.1有，dp(Γ)=1，由定理 3.2知ip(Γ)=1，从而有rp(Γ)=0；反之，若存在某个n维概率分布列 p，有rp(Γ)=0，则由知，dp(Γ)=1且ip(Γ)=1，由定理3.2知Γ是不相容理论。

（2）设Γ是相容理论，则对于任取的n维概率分布列 p，由定理3.2知，ip(Γ)=0，故有，注意到0≤dp(Γ)≤1，则这时；反之若存在n维概率分布列 p，有，则 有ip(Γ))≤1，若ip(Γ)=1，则由定理3.2知Γ是不相容理论，这时由定理3.1得dp(Γ)=1，这样就得dp(Γ)(1+ip(Γ))=2矛盾，故得ip(Γ)=0，即Γ是相容理论。

另一方面，取Γ1=S，取n维概率分布列p为均匀分布，则由以上的讨论知dp(S)=1，又知对于相容理论有ip(S)=1，从而得；设Γ完全由定理组成，则对于2任取的n维概率分布列p都有dp(Γ2)=0，由定理3.2知ip(Γ2)=0，故得rp(Γ2)=1，于是就证明了对于相容理论的相容度1和是可达的。证毕。

4 结束语

本文在n值Lukasiewicz命题逻辑系统中对理论的随机相容度展开研究，利用已有的命题公式的随机真度的和随机伪距离的概念和性质，给出了理论的随机直径的概念，并指出其随机直径是和概率分布列的取值相关的，提出了理论的随机相容度概念，由随机相容度的定义知理论的随机相容度也依赖于n维概率分布列的取值，虽然如此，理论的随机相容度也能保持其在经典逻辑空间的基本性质。在n值随机逻辑度量空间中继续研究理论的随机相容度的分布等工作，是艰难和十分有意义的，将另文讨论。

[1]Wang G J，Zhang W X.Consistency degrees of finite theories in lukasiewicz propositional fuzzy logic[J].Fuzzy Sets and Systems，2005，149：275-284.

[2]Zhou X N，Wang G J.Consistency degrees of theories in some systems of propositional logic[J].Fuzzy Sets and Systems，2005，152：321-331.

[3]Zhou H J，Wang G J.A new theory index based on deduction theorems in several logic systems[J].Fuzzy Sets and Systems，2006，157：427-443.

[4]惠小静，李宏设，李丽.D-逻辑度量空间中的相容理论[J].模糊系统与数学，2009，23（2）：12-17.

[5]李修清，吴果林.ξ-逻辑度量空间中理论的开放度[J].桂林航天工业学院学报，2014，19（2）：152-155.

[6]惠小静，王国俊.经典推理模式的随机化研究及其应用[J].中国科学：E辑，2007，37（6）：801-812.

[7]惠小静，王国俊.经典推理模式的随机化研究及其应用（II）[J].模糊系统与数学，2008，22（3）：21-26.

[8]惠小静.三值R0命题逻辑系统的随机化[J].应用数学学报，2009，32（1）：19-27.

[9]惠小静，王国俊.D-逻辑度量空间与近似推理[J].南京大学学报数学半年刊，2007，24（2）：249-257.

[10]李修清，魏海新，林亮.修正的n值Gödel逻辑系统的随机化[J].计算机工程与应用，2012，48（24）：45-49.

[11]李修清，朱宁.R0型命题逻辑系统的随机化[J].模糊系统与数学，2013，27（1）：63-70.

[12]李修清，魏海新.n值Lukasiewicz逻辑系统中理论的随机发散度[J].模糊系统与数学，2013，27（6）：93-98.

[13]王国俊.数理逻辑引论与归结原理[M].2版.北京：科学出版社，2006.

[14]王国俊.非经典数理逻辑与近似推理[M].2版.北京：科学出版社，2008.

[15]Hamilton A G.Logic for mathematicians[M].New York：Cambridge University Press，1978.