一类Keller-Segel趋化模型的分支结构

高海燕

兰州财经大学 统计学院，兰州 730020

1 引言

生化研究证明：在趋化因子作用下，生化系统会从均匀稳定态变成不稳定的，从而导致系统斑图生成。这种机制可以由一个简化的化学反应网络（Chemical Reaction Network，CRN）来描述，即 Keller-Segel模型[1-5]。趋化模型的一个重要性质是它丰富的斑图性质，在本文中，试图考虑一类有失稳均匀稳定态的CRN，即一类带Logistic源项的具有非线性信号动力学趋化模型[6]：

类似的趋化失稳机制将导致斑图生成。这里Ω⊂ℝn是一个具有光滑边界∂Ω的有界区域。d1,d2,χ,α,β和γ均为正常数。u(x,t)和v(x,t)分别表示细胞密度和化学引诱剂的含量，d1和d2是扩散率，χ表示趋化敏感性系数。α表示细胞的线性增长率，γ表示在稳态条件下细胞的密度，β控制化学引诱剂的生成。这里假设随着细胞密度的增加化学物质的生产达到饱和，这将防止化学引诱物随着细胞密度的增加而过度产生。

在二维空间中，文献[6]讨论了模型（1）的有限振幅、稳态和空间异构解，并且通过数值模拟显示，在趋化作用下该模型可以产生丰富且复杂的空间斑图。通过关注边界条件的作用以及比例与高宽比的影响，文献[7]研究了模型（1）的斑图时空动力学。当α=0,1/γ→0时，模型（1）退化为经典Keller-Segel模型。最近，文献[8-9]分别讨论了仅带Logistic源项的Keller-Segel模型（1）的非线性不稳定性及斑图生成。对仅具有非线性信号动力学的趋化模型（1），文献[10]研究了正常数平衡点的稳定性;同时，文献[11]考虑了不稳定正常数平衡解附近的非线性动力学性态。文献[12-14]也讨论了具有一般信号生成机制和高密度下细胞退化的趋化模型的趋化交错扩散的影响。本文将应用Crandall和Rabinowitz的局部分支理论[15]，主要考虑模型（1）在矩形区域上的分支问题。以趋化敏感性系数χ为分支参数，在二维空间区域详细讨论非常数正平衡解的结构以及刻画时空斑图的演化。

2 分支点

易知模型（1）有平凡解（0，0）及唯一正常数平衡解

模型（1）的平衡态问题为：

定义Hilbert空间：

F关于(u,v)在点Ec处的Fréchet导算子记为：

式（2）在Ec处的线性化系统是：

其中(h,k)∈X，且h,k≠0。将h和k表示为Fourier展式形式，即

其中

将式（4）代入式（3），则(hmn,kmn)满足：

因此，式（3）有非零解当且仅当对某个m,n，式（7）有非零解，即对某个m,n。

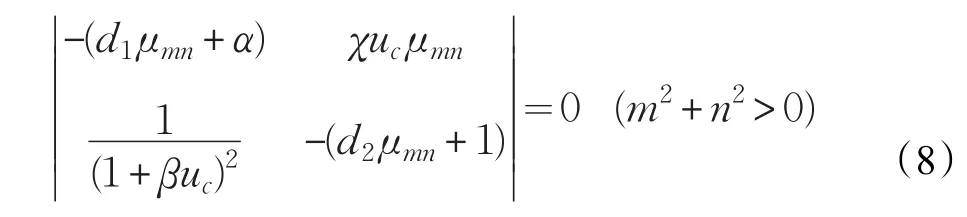
从而，当且仅当

时算子F(u,v)(χ;uc,vc)退化。

因此，当 χ=χ(m,n),m,n=0,1,2,…,(m2+n2≠0)时，(χ(m,n),uc,vc)是可能的分支点。例如，χ(1,0)=此时，dimkerF(u,v)(χ(1,0))=dimkerF(u,v)(χ(0,1))=1。注意到 (m,n)↦χ(m,n)不是一一对应的，如 χ(1,1)=χ(2,0),χ(3,1)=χ(0,2),χ(1,3)=χ(5,1)=χ(4,2)。所以，当参数满足适当条件时，有dimkerF(u,v)(χ(m,n))≥2。

3 分支解的存在性

当利用Crandall和Rabinowitz[15]的局部分支定理时要求核空间维数为一维，故当考虑如χ(1,0)或χ(0,1)的情形时，只要选取m,n使得dimkerF(u,v)(χ(m,n);uc,vc)=1。

定理3.1如果dimkerF(u,v)(χ(m,n);uc,vc)=1，则存在一个正常数δ使得系统式（2）在点(χ(m,n);uc,vc)的邻域中的非常数正解可以表示为：

其中φm(x)和ψn(y)由式（5）给出，并且

证明由dimkerF(u,v)(χ(m,n);uc,vc)=1和式（7）可知：

记算子F(u,v)(χ(m,n);uc,vc)的伴随算子为：

类似于前面的计算过程可得：

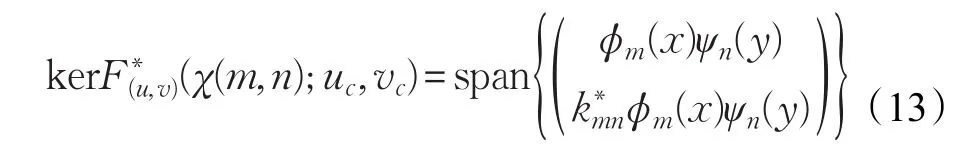
从而codimRangeF(u,v)(χ(m,n);uc,vc)=1进一步，对F(u,v)(χ(m,n);uc,vc)关于χ求导得：

注意到

所以

由局部分支定理知，系统式（2）存在一条由点(χ(m,n);uc,vc)分支出的非平凡解曲线(χ(s),u(s),v(s))，并且它是点(χ(m,n);uc,vc)邻域中唯一的解曲线，其中

为方便，记Φ(x,y)=φm(x)ψn(y)，注意到(s)和(s)实际也是 x,y 的函数，即(s)=(x,y,s),(s)=(x,y,s),又有：

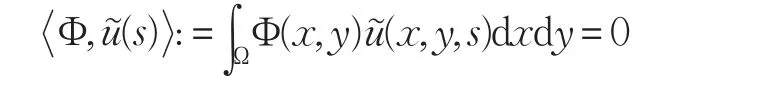
将分支解(χ(s),u(s),v(s))代入式（2）的第一个方程中，并关于s求两次导数得：

在式（15）中取s=0得：

运用Green’s公式可计算得：

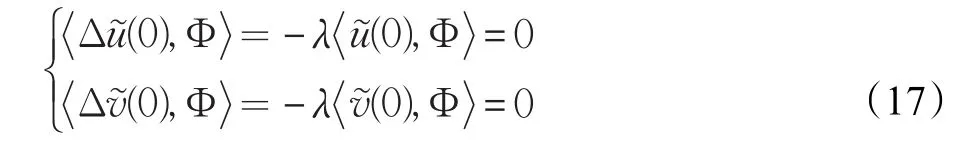
和

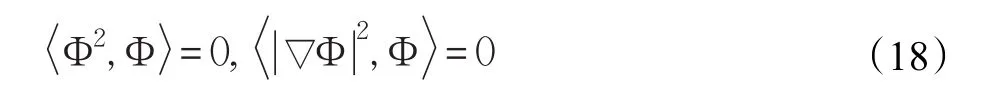
其中λ在Ω上满足-ΔΦ=λΦ。式（16）与Φ作L2内积，并结合式（17）与式（18）有：

因此η(0)=0。定理3.1证毕。

4 分支方向

考虑定理3.1中所得到的局部分支解式（10）在点(χ(m,n);uc,vc)处相应于平凡解曲线Γ的分支方向。若，则称分支式（10）为超临界的；若，则称分支式（10）为次临界的。下面将给出(0)的具体表达式。以下记

为证明定理4.1，需先证明如下引理成立。

引理4.1式（9）中的(A,B,C,D)满足如下代数方程：

证明由分部积分可得：

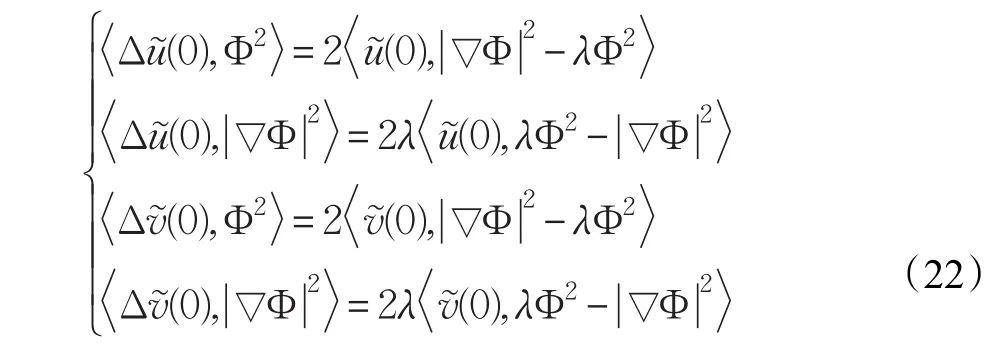
式（16）与Φ2作L2内积得：

式（2）的第二个方程关于s求导两次，并令s=0得：

进一步，式（24）与Φ2作L2内积可知：

式（16）和（24）分别与 ||∇Φ2作L2内积得：

结合式（23）和式（25）～（27），以及式（19）中关于(A,B,C,D)的定义知式（21）成立。引理4.1证毕。

证明定理4.1对式（15）关于s求导并令s=0得：

上式与Φ作L2内积，又利用可得：

从而定理4.1得证。

5 结论

本文主要讨论了一类带Logistic源项的具有非线性信号动力学趋化模型在正常数平衡解(uc,vc)处的分支问题。在矩形区域上，运用Crandall和Rabinowitz的局部分支理论，以趋化敏感性系数χ为分支参数，对二维情况下非常数正平衡解的结构给出了细致的刻画。

[1]Keller E F，Segel L A.Initiation of slime mold aggregation viewed as an instability[J].Journal of Theoretical Biology，1970，26（3）：399-415.

[2]Keller E F，Segel L A.Model for chemotaxis[J].Journal of Theoretical Biology，1971，30（2）：225-234.

[3]Horstmann D.From 1970 until present：The Keller-Segel model in chemotaxis and its consequences I[J].Jahresber Dutsch Math Ver，2003，105（3）：103-165.

[4]Horstmann D.From 1970 until present：The Keller-Segel model in chemotaxis and its consequences II[J].Jahresber Dutsch Math Ver，2004，106（2）：51-69.

[5]Bellomo N，Bellouquid A，Tao Y，et al.Toward a mathematical theory of Keller-Segel models of pattern formation in biological tissues[J].Mathematical Models&Methods in Applied Sciences，2015，25（9）：1663-1763.

[6]Maini P K，Myerscough M R，Winters K H，et al.Bifur-cating spatially heterogeneous solutions in a chemotaxis model for biological pattern formation[J].Bull Math Biol，1991，53（5）：701-719.

[7]Myerscough M R，Maini P K，Painter K J.Pattern formation in a generalized chemotactic[J].Bull Math Biol，1998，60（1）：1-26.

[8]Fu Shengmao，Liu Ji.Spatial pattern formation in the Keller-Segel model with a logistic source[J].Computers&Mathematics with Applications，2013，66（3）：403-417.

[9]Kutoa K，Osaki K，Sakurai T，et al.Spatial pattern formation in a chemotaxis-diffusion-growth model[J].Physica D，2012，241（19）：1629-1639.

[10]Hillen T，Painter K J.A user’s guide to PDE models for chemotaxis[J].Journal of Mathematical Biology，2009，58（2）：183-217.

[11]高海燕.一类非线性信号动力学趋化模型的非线性不稳定性[J].应用数学，2016，29（1）：125-135.

[12]Nakaguchi E，Osaki K.Global existence of solutions to a parabolic-parabolic system for chemotaxis with weak degradation[J].Nonlinear Analysis Theory Methods&Applications，2011，74（1）：286-297.

[13]Nakaguchi E，Osaki K.Global solutions and exponential attractors of a parabolic-parabolic system for chemotaxis with subquadratic degradation[J].Discrete and Continuous Dynamical Systems Serise B，2013，18（10）：2627-2646.

[14]Nakaguchi E，Osaki K.Lp-estimates of solutions to ndimensional parabolic-parabolic system for chemotaxis with subquadratic degradation[J].Funkcialaj Ekvacioj，2016，59（1）：51-66.

[15]Crandall M G，Rabinowitz P H.Bifurcation from simple eigenvalues[J].Journal of Functional Analysis，1971，8（2）：321-340.