极限思维在解题中的应用

☉江苏省张家港市沙洲中学 洪晓鸽

极限思维是解决一些特殊数学问题的一种重要的数学思想.解题过程中，若能灵活地借助极限思想处理一些相关问题，利用从有限到无限，从近似到精确，从量变到质变，往往可以有效避开抽象、复杂的讨论与运算，降低难度，优化过程，进而得以快速破解问题，起到事半功倍的效果.

一、方程中的极限思维

例1 函数f（x）=lnx+ex的零点所在的区间可能是下面中的（ ）.

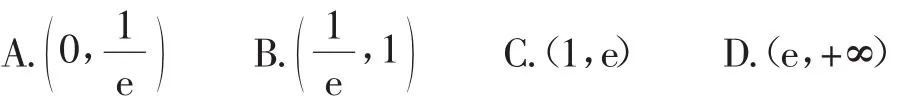
分析：通过计算，结合函数（fx）=lnx+ex在各选项中相应点函数值的正负情况，结合根的存在定理得以确定零点所在的区间，而对于特殊点0，+∞，经常可以采用极限思维加以处理.

点评：本题主要考查根的存在性定理，函数的零点及其应用.解决此类问题的方法技巧主要有两种：（1）通过函数的图象加以直观确定；（2）结合根的存在定理加以运算判断.利用极限思维来处理函数的零点问题，回避困难计算，以巧取胜.

二、函数中的极限思维

分析：常规方法是直接通过函数的解析式的特点来确定函数的图象问题，判断难度不小.而通过自变量x的取值的极限性来分析图象的走势，可以比较简单快捷、直观形象地确定答案.

故选择答案：B.

点评：本题采用极限思维，通过自变量x的两个变化极限所对应的因变量y的取值情况，结合选项中的相关图象来排除即可.极限思维在解决函数的图象问题时，关键在于根据题目条件，考虑相应函数中的解析式、图象、函数值等的极限取值，并结合所对应的极限取值，利用函数的相关知识来解决，淡化函数的运算与变换过程，降低难度.

三、解析几何中的极限思维

例3 （2016·浙江文·13）设点F1，F2分别是双曲线左、右焦点.若点P在双曲线上，且△F1PF2为锐角三角形，则|PF1|+|PF2|的取值范围是______.

分析：采用常规方法求解难度比较大且计算繁杂，而从双曲线的定义入手，通过分类讨论，结合极限思维分别确定当∠F1PF2与∠F1F2P为极限值90°时，对应关系式|PF1|+|PF2|所对应的极端值，数形结合即可得到△F1PF2为锐角三角形时对应关系式|PF1|+|PF2|的取值范围.

解析：由题可得a=1，b= ■ 3 ，c=2，不失一般性，假定P是双曲线1上第一象限内的点，结合双曲线的定义有|PF1|-|PF2|=2a=2，可得|PF1|=|PF2|+2，下面通过极限思维来讨论：

（1）当∠F1PF2=90°时，由勾股定理可得|PF1|2+|PF2|2=|F1F2|2，整理则有|PF2|2+2|PF2|-6=0，解得|PF2|=-1（负值舍去），此时|PF1|+|PF2|=2；

（2）当∠F1F2P=90°时，由勾股定理可得|PF1|2=|PF2|2+|F1F2|2，解得|PF2|=3，此时|PF1|+|PF2|=8；

而由题知△F1PF2为锐角三角形，结合极限思维并数形结合可得|PF1|+|PF2|∈（2，8），

点评：本题采用极限思维，根据曲线上的点的移动所对应的直角三角形的极端元素入手，结合极端情况下所对应的直角三角形的三边之间的关系来转化.极限思维在解决解析几何问题时，可以结合极端元素条件下的解析几何的相关知识来转化与应用，化一般为特殊，这样操作起来思维清晰，难度降低，过程简洁，最后又要从特殊回归到一般，从而使得问题得以正确解答.

四、立体几何中的极限思维

例4 正三棱锥S—ABC相邻两侧面所成的角为α，则α的取值范围是（ ）.

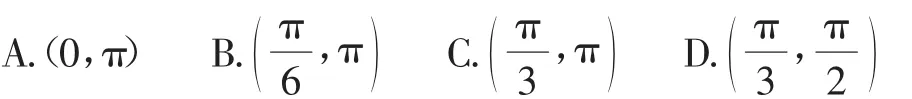
分析：直接处理存在一定的难度，而且非常考验直观想象能力与分析问题处理问题的能力.而以动制静，利用SO的大小变化极限思维来分析在两个极端情况下，对应的相邻两侧面所成的角的取值情况，从而得以快捷判断.

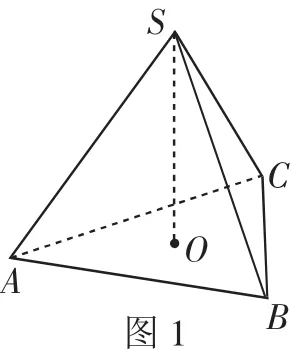
解析：在正三棱锥S-ABC中，如图1所示，SO⊥底面ABC，O为正△ABC的中心，当SO→0时，此时正三棱锥S-ABC的高趋近于0，结合图象可知，相邻两个侧面的夹角趋近于π，当SO→+∞时，此时正三棱锥S-ABC的高趋近于+∞，结合图象可知，此时正三棱锥S-ABC无限接近于一个正三棱柱，数形结合可知其相邻两个侧面的夹角无限接近

故结合极限思维并数形结合可知，正三棱锥相邻两个侧面所成角的取值范围选择答案：C.

点评：运用运动观点、极限的思想去观察、分析、处理问题，直接利用极端位置所对应的角度来分析，省去空间几何图形的直观想象，同时也省去相应的运算求解，可达到意想不到的效果.

五、组合中的极限思维

分析：根据创新定义，结合组合数公式加以分析与判断，同时解答时还要根据极限的思维加以分析.

点评：解决此类创新定义问题，必须按照一定的数学规则和要求，结合相关知识加以创新，同时按照一定的数学规则和要求、结合各相关数学知识加以逻辑推理和计算等，从而得以解决问题.而在处理过程中，有时非常规问题就得用非常规的方法，利用极限思维来处理相应的取值极限，也是非常巧妙的方法.

其实，利用极限思想，在实际求解一些特殊数学问题时可以避免复杂运算，探索解题新思路，大有“拨开云雾见晴天”的美好感觉.特别在解决一些数学问题中，利用极限思维来考虑极端情形，可以以动制静，简化计算，化繁为易，达到巧妙、快捷、正确解答的目的，拓展思维，培养能力.