基于谐波窗函数的桥梁振动信号分解与重构

叶 飞， 吴加权， 张馨予， 肖 驰， 马 琨

(昆明理工大学 建筑工程学院，昆明 650500)

桥梁在公路与铁路运输系统中扮演着重要的角色。然而，由于受施工质量、环境、工作负荷、工作年限等诸多因素影响，必将导致结构性能下降甚至出现缺陷，进而危害到桥梁安全。因此，融合了信号处理技术的结构健康诊断(Structural Health Monitoring,SHM)成为了广大学者关注和研究的热点问题，它对于预防灾难发生及为损伤桥梁提供廉价有效的维修方案具有积极意义。损伤检测，是SHM的主要研究领域之一[1]。从复杂信号中提取出有效信号是进行损伤检测的重要前提之一。

近年来，越来越多的学者选择采用基于振动理论的研究方法开展相关研究[2-3]。这些方法主要通过研究结构在振动过程中损伤前后各模态参数(如固有频率、模态振型、模态阻尼)的变化来进行损伤的定位识别[4]。Messina等[5]研究发现，通过研究结构固有频率的变化，可以实现损伤检测；Pakrashi等[6]提出了利用小波变换实现基于模态振型的直接损伤检测方法；Hu等[7]通过对比桥梁损伤前后模态振型变换进行了损伤识别。在此基础上，众多学者又开发出了许多敏感性更高的损伤检测指标。郭惠勇等[8]对基于模态应变能的3种损伤指标进行了对比分析；Bayissa等[9]用弯矩响应功率谱作为损伤指标对二维板类结构进行了损伤检测；余竹等[10]利用Lipschitz指数在识别信号奇异性上的优越性，结合位移模态的小波变换对裂缝梁的损伤识别效果进行了研究。

虽然，众多学者在损伤方法及检测指标方面做了大量的研究工作，但不可回避的一个现实问题就是，作为分析基础的数据即检测信号(位移、速度、加速度等)的有效性问题。在实际检测过程中，由于外界或仪器本身干扰，往往信号的信噪比较差；或者，由于结构损伤程度较轻，因此损伤造成的信号变化非常微弱；再或者，由于测量时间较长，使得损伤造成的信号变化在整个测量数据中占比较少，导致信号处理过程中被其他信号淹没。因此，信号的质量对后期的分析结果及精度有较大影响。为了克服以上问题，学者们引入了信号处理相关技术，并与传统工具相结合进行了大量的研究工作。孙增寿等[11]将小波变换与曲率模态相结合利用小波变换系数残差构建损伤检测指标实现了桥梁损伤定位；余竹等将小波变换与Lipschitz指数相结合提高裂缝损伤识别的敏感性；刘习军等[12]运用小波变换对振动模态分析中叠加的多阶模态信息进行了有效分离；Han等[13]的研究结果表明，运用希尔伯特-黄变换(HHT)结构的模态参数进行提取并进行损伤识别是可行的和有效的；Zhang等[14]利用HHT对检测信号进行了分解得到了各频段的频率时间关系，并以此为基础利用固有频率变化率实现了多裂缝损伤的识别。

尽管小波变换与HHT技术的引入丰富了损伤检测的方法提高了识别精度，但实际应用过程仍存在一些需要改进的地方。比如：由于许多小波母函数本身没有明确的时域和频域数学表达式，造成了频段划分时频带的混叠；在一些奇异信号的识别中，小波母函数的选取对信号重构的结果影响较大，小波母函数选取不当容易导致重构信号的失真[15]；小波变换的频带划分必须满足fm/2n这一约束条件的限制，导致频带宽度无法满足要求；当频带划分较小时，无论小波变换还是HHT都需要不断的迭代计算，计算时间长。因此，本文提出了一种基于谐波窗函数的信号分解与重构方法，该方法对信号提取过程中出现的，信号失真、相移、频带划分受限以及计算量大等问题有所改进。

1 谐波小波及谐波小波包变换

一些新的研究表明：基于信号处理技术对桥梁振动信号进行分解与重构，对提取出的低阶振动信号也可以实现桥梁的损伤检测。小波变换在信号分解、放大以及瞬态信号的检测方面具有明显优势，但由于许多小波母函数本身没有明确数学表达式且分解后易出现频带混叠。因此，Newland于1993年提出的一种以正交小波函数(谐波小波)为母小波的谐波小波变换。

谐波小波函数的频域表达式为：

(1)

式中：n=2(j+1),m=2j,j∈Z+。对式(1)做傅里叶逆变换，即可得到谐波小波的时域表达式：

由式(2)可以看出ψ(m,n)(t)是一个实部为偶函数，虚部为奇函数的复小波函数，它具有零相移的特点。对于离散信号s(r),(r=0,1,2,…，N-1)，其谐波小波变换的时、频域表达式分别为：

(2)

为了提高运算效率E. Newland给出了谐波小波的快速计算方法：首先，根据需求确定信号拟分析频段的范围；其次，利用式(1)计算相应频段谐波小波的频域表达式Ψm,n(ω)；再次，计算信号的频谱(r)，第四，利用式(3)计算各频段信号的小波变换频谱值最后，对进行傅里叶逆变换即可得到相应频段的时域信号。

(3)

根据以上公式及计算方法，可得知谐波小波(包)变换与传统小波(包)变换相比的三大优势：① 谐波小波(包)在频域具有严格的盒形谱，避免了分解后频带的混叠；② 经过谐波小波(包)变换后的信号相移为零；③ 采用谐波小波(包)变换后的信号与原始信号相比，不会出现数据点数的损失。

谐波小波(包)与传统小波(包)变换的主要区别在于小波母函数的不同，因此谐波小波变换在信号的分解过程中同样存在分解后频段宽度必须满足fm/2n这一条件限制的问题(fm为分析频率，即采样频率的1/2)。图1为谐波小波(包)分解时频段分布图，图中j=1时，谐波小波与谐波小波包分解的频段划分是一致的，当j>1时，谐波小波分解不会对大于fm/2部分的进行分解，而谐波小波包则会继续按fm/2n继续进行划分。

图1 谐波小波(包)分解频段分布图Fig.1 Frequency distribution of harmonic wavelet(packet) decomposition

1994年，Newland已经将二进制谐波小波(包)推广到了广义谐波小波(包)[16-17]。使得谐波小波(包)的频段宽度由fm/2n变成了fm/n。这样的频段划分方式，虽然可在整个频段内对信号进行无限细分，但若拟分析信号恰好在两相邻频段均有分布，则会给信号的分析带来诸多不便。因此，谐波窗函数的构建即是为了实现频带的自由划分。

2 谐波窗函数

基于广义谐波小波(包)，本文采用构建谐波窗函数的方法进行桥梁振动信号的提取，具体方法如下：

2.1 谐波窗函数的构建

设原始信号中拟分析的频段带宽为B，则：

B=fh-fl

(4)

式中:fh，fl分别为拟分析频段的频率上限与下限。

由于离散信号s(r)在做傅里叶变换后，其频谱具有对称性，其实部为偶函数，虚部为奇函数。因此，在构建谐波窗函数时，其频域数据序列也为对称形式，其频域图形，如图2所示。

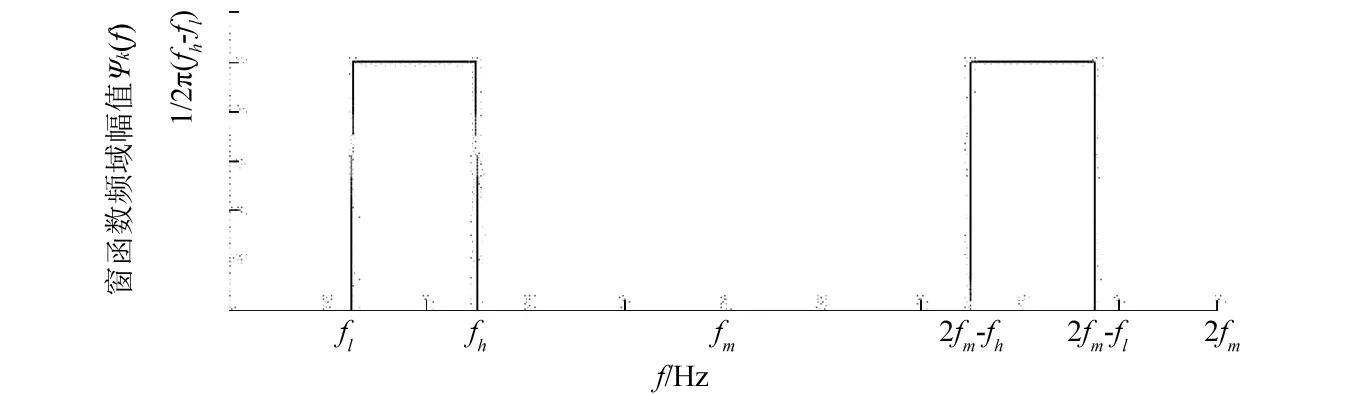
图2 谐波窗函数频域图Fig.2 Frequency domain of harmonic window function

2.2 基于谐波窗函数的信号分解的实现过程

(1)构建谐波窗函数

针对桥梁低阶振动信号进行损伤识别时，分析的主要研究对象为各阶次固有频率部分。因此，在根据公式(5)进行谐波窗函数在构建时，fl与fh的选择可参照振动信号频谱中各阶次固有频率的位置进行选择。

Ψfl,fh(k)=

(5)

(2)对原始信号做快速傅里叶变换(FFT)

对原始信号s(r)做FFT变换，得到其频谱序列S(k),(k=0,1,2,…，N-1)。

(3)计算分析频段的谐波小波变换

分析频段的谐波小波变换系数可由式(6)计算得出：

(6)

由于，FFT后的频域数据序列具有对称性，若需要对分析频段的频域信号进行分析，式(7)表达的数据序列即为谐波小波变换后频谱；

(7)

若需要对分析频段的时域信号进行分析，为了保证数据的完整性，则需要对式(8)表达的数据序列进行快速傅里叶逆变换(IFFT)得到。

(8)

对于广义谐波小波变换，当频带无交叠时，各频段的小波变换是正交的。谐波窗函数的构建基于广义谐波小波，且本文分析对象为桥梁振动时各阶次固有频率所在频段的信号，因此采用本方法进行分解后的各频段信息也必然是正交的。另外，采用谐波窗函数分解时，与关注频段无关的信息已全部归零，所以分解过程中噪声信号也一同被过滤了。

3 桥梁振动信号的谐波窗函数分解与重构实验

3.1 信号采集

原始信号数据来自于一根600 cm×25 cm×50 cm的钢筋混凝土梁(下文简称梁)的振动实验。梁的密度为2.5×103kg/m3，混凝土保护层厚度为40 mm，受压纵筋2×Ø20，受拉纵筋3×Ø20，箍筋Ø8，配置间距200 mm。梁的几何尺寸如图3所示。

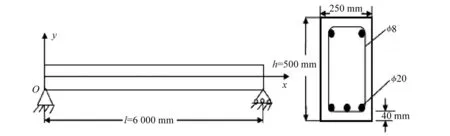
图3 梁几何尺寸示意图(mm)Fig.3 Beam geometry size(mm)

实验通过使用24磅铁在梁顶部进行随机敲击的方法对梁进行激励，使梁产生振动以采集其动态应变信号。信号采集实验共设11个测点，每测点包含沿x方向与y方向的电阻应变计各一片(其中x方向为测量片，y方向为补偿片)。实验装置如图4所示。

图4 信号采集实验装置图Fig.4 Device diagram signal collection experiment

应变计均布置于梁底部，相邻测点间距为50 cm。测点分布情况，如图5所示。

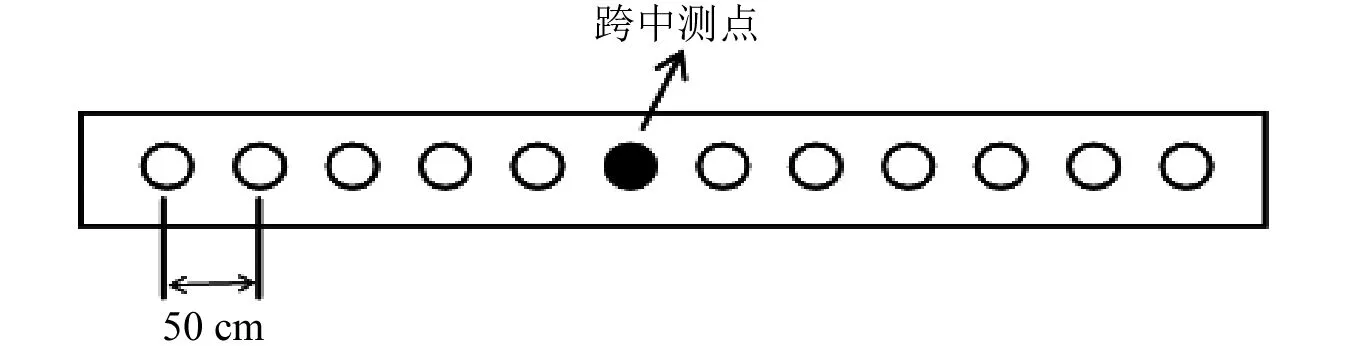
图5 测点分布图Fig.5 Distribution of measuring points

应变计电压信号的采集，通过DH5922动态信号测试分析系统完成。由于各测点数据的分解与重构方法相同，下文以梁底部跨中位置处应变计测量的电压信号数据(即图5中实心圆点所对应测点的数据)为例展示信号处理效果。

信号采集参数设定如下：采样频率为2 kHz，采集时长437 s，传感器类型为应变测量，信号类型为电压采集,mV，采集方式为连续采集，数据点数874 448。图6为原始信号的时域图与频谱图。

改革开放四十年来，在中国新大学运动发展过程中产生的这些问题，既需要在“内涵”建设、“新大学”精神和学校定位三个“术”的方面下功夫，同时也需要在“道”的层面对新大学进行深层次的反思。

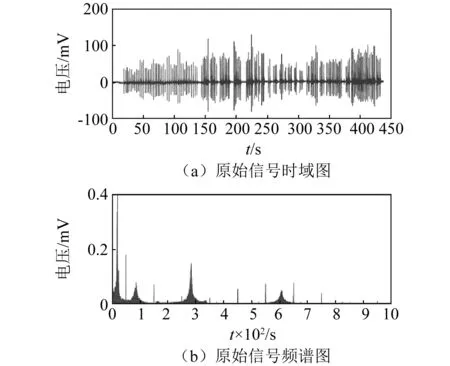
图6 原始信号时、频域图Fig.6 time-frequency domain of original signal

图6(a)为采集的原始时域信号，纵坐标为应变计采集到的电压mV；横坐标为时间t，s。在对时域信号做快速傅里叶变换后，我们可以获得它的频谱信息。由图6(b)可以看出，梁的前五阶固有频率分别在19.6 Hz、86.3 Hz、164.9 Hz、284.2 Hz、608.3 Hz。

若要采用传统二进制小波(包)变换进行分解，则需要对信号进行4层分解才可将5阶信号分解到独立频带内。分解后5阶信号所在节点号及频段范围如表1所示。表1中小波(包)变换的频段根据公式fm/2n划分，谐波窗函数法的频段，以频率幅值下降到各阶次固有频率中心幅值的20%时对应的频率值作为频段的上、下限频率(即式(5)中的fh，fl)。

3.2 一阶信号分解重构后结果对比

由表1可以看出，二进制小波与小波包分解后频段范围对前两阶信号来说没有区别，而对后三阶及以后信号来说，小波包分解的频段更窄，包含的干扰信号也更少。因此，本文选用小波包变换的频带划分范围，分别选用谐波窗函数与小波包对信号进行分解与重构。

表1 各阶次信号分解后频段分布情况Tab.1 Frequency distribution of decomposed five order signals

基于小波包变换对实验信号进行分解与重构可利用MATLAB软件中的小波工具箱完成，其实现过程如下：

1) 分别选择小波基函数为db10小波与哈尔小波，对原始信号进行4层分解。得到16节点的小波包分解树，第4层节点编号依次为(4，0)，(4，1)，…，(4，15)。完成对信号的分解。

3) 利用工具箱提供的单节点重构函数对(4，0)节点的信号进行重构，使其数据量由原始信号的1/16恢复为原始大小。一阶信号重构完成。

基于谐波窗函数进行信号分解与重构的过程如下：

1) 构建谐波窗函数。分别设fl，fh为0 Hz和62.5 Hz，根据式(5)定义[1 0 1]型数组。

2) 利用快速傅里叶变换计算原始信号的频谱，得到其频谱序列。

3) 根据式(6)，将第1步定义的[1 0 1]型数组与第2步得到的频谱序列相乘并乘以补偿系数125π，得到0～62.5 Hz频段信号的频谱序列，完成信号的分解。

4) 对第3步得到频谱序列作快速傅里叶逆变换，实现该频段信号的重构。

实验结果如图7所示。

图7为0～62.5 Hz频段信号经分解重构后136.6 s～137.5 s内的时域信号，其中(a)图为原始信号、(b)图为哈尔小波包分解结果、(c)图为“db10”小波包分解结果、(d)图为谐波窗函数分解结果。由图7可以看出：

(1)分解重构后的信号波形基本一致，但与原始信号相比高频信息(即波形中毛刺)明显减少。说明两种方法均实现了一阶振动信号的提取。

(2)(b)、(c)图的最大振幅在50 mV左右，与原始信号最大振幅接近，(d)图中最大振幅为20 mV左右。其原因在于经过4层分解后，利用小波包变换得到的单节点的数据量降为了原始数据量的1/16(54 653个数据)。小波工具箱中单节点重构函数在重构过程中利用插值算法将数据量恢复到了原始数量(87 448个数据)，使得信号能量增加，振幅增大。谐波窗函数法在分解与重构的整个过程中数据量始终无损失，无需插值。在将高频信号去除后，必然出现信号能量减小，振幅降低的情况。说明谐波窗函数法分解重构后的结果更接近真实信号。

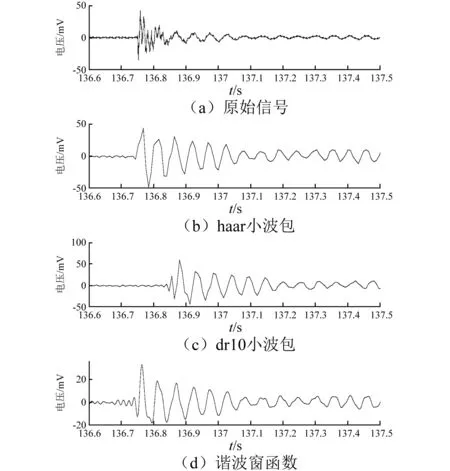
图7 一阶振动信号分解重构后时域图Fig.7 The first order vibration signal decompositionand reconstruction in time domain

(3)由(a)图可以看到，在梁受到激励后，信号波形中首先出现的是波谷，(b)、(c)图的波形中首先出现的均为波峰，而(d)图中很好的提取到了波谷信息；(d)图中的波形与(b)、(c)图相比更加平滑。其原因在于，传统小波包分解为了便于计算机进行编码与压缩，其变换过程实质上为隔点采样过程。当振动信号出现在两次采样之间时容易导致有用信息的漏采；同时，由于数据量有所减少，所以信号失真程度也必然有所增大。虽然，小波工具箱提供的重构函数通过插值较好的改善了这一问题，但重构信号与真实信号仍然有一定差异。谐波窗函数法在分解与重构的整个计算过程中均对所有数据统一运算，有效避免了振动信号的遗漏。说明谐波窗函数法分解重构后的结果失真更小。

(4)(c)图与(b)图相比，在振幅最大的波峰前多了一个小的波峰，且整个波形存在一定差异，其中波峰与波谷处最为明显。其原因主要在于小波母函数的选取不同。说明选择不同的小波母函数将导致分解结果的不一致，为后期分析结果的准确性带来影响。

(5) (a)图与(d)中波形起振点出现在136.75 s，(b)图出现在136.73 s，(c)图出现在136.85 s。结果表明，传统小波包变换分解后的信号出现了相移，其中“db10”小波的分解结果相移最为明显。说明传统小波包分解法易带来信号的相移，且相移程度与小波母函数的选取有关，而谐波窗函数法实现了很好的锁相功能。

3.3 基于谐波窗函数的5阶振动信号分解与重构

由图6中(b)图可以发现，在0～62.5 Hz频段仍然包含有大量噪声，特别是50 Hz处有一明显噪声，而且在整个频段内存在大量的50 Hz的倍频干扰噪声。所以，图7中(d)图的波形中仍然存在一些小的畸变。根据表1中最后一列的频段范围确定窗口大小，构建谐波窗函数(由于各阶次信号对应的分解频段均不从0 Hz开始，故此时谐波窗函数变为[0 1 0 1 0]型)。采用谐波窗函数法，按照3.2节中分解重构步骤对5阶振动信号再次进行分解与重构。其结果如图8、图9所示。

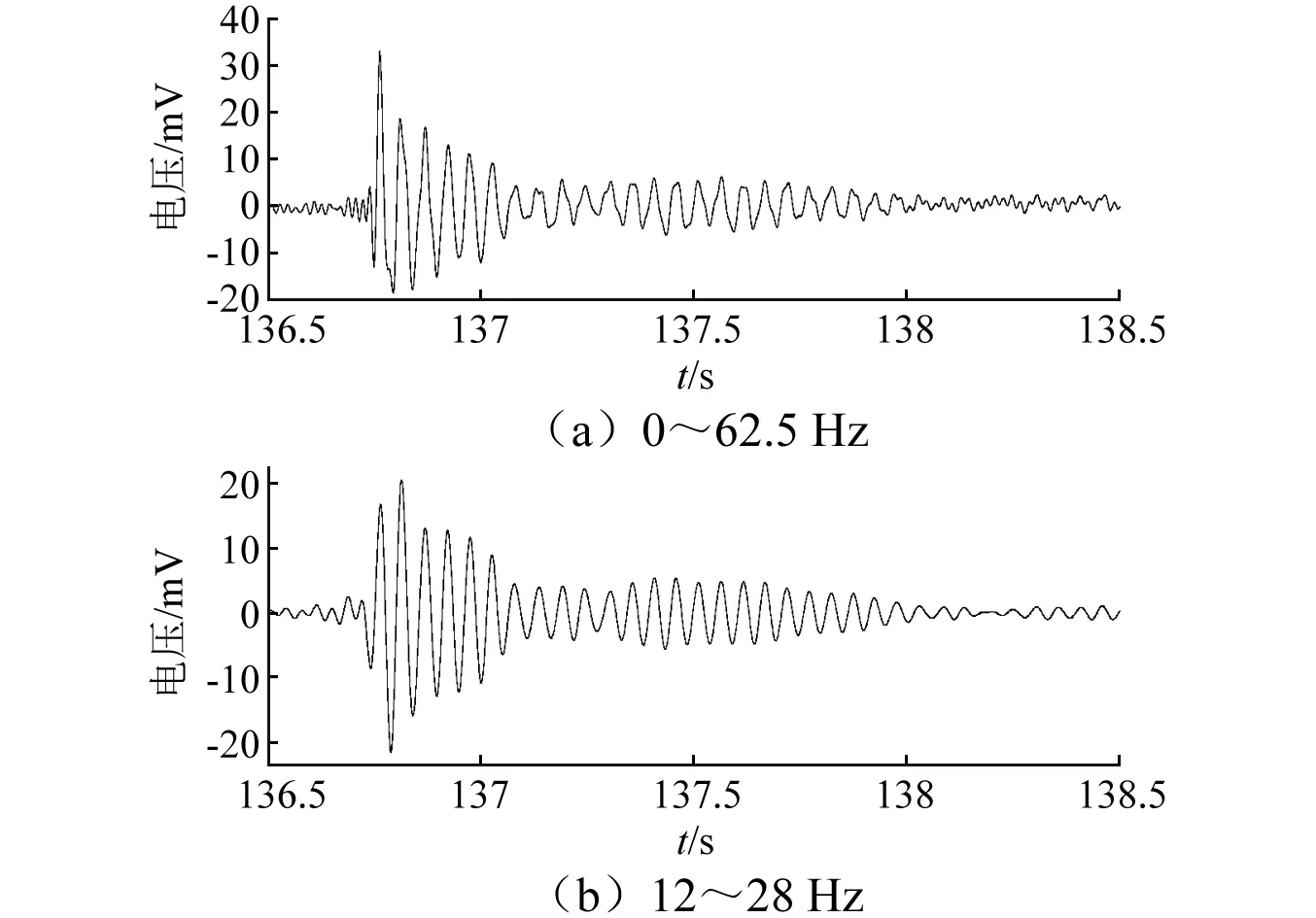
图8 一阶振动信号对比图Fig.8 Comparison of first order vibration signals

图8为一阶振动信号分别在0～62.5 Hz与12～28 Hz范围内分解重构的时域信号对比图，其中(a)图与图7中(d)图相同。(a)图中，首个波峰的幅值超过33 mV，随后波峰从19 mV开始依次衰减；波谷最小值为-19 mV，随后依次衰减，波峰与波谷的包络出现了一定的“不对称”现象；波峰与波谷附近的波形出现了畸变。(b)图中，首个波峰幅值下降为16 mV，第二个波峰为19 mV，波谷最小值为-21 mV，波峰与波谷的包络表现出一定的“对称”性；各波峰与波谷波形的畸变现象消失，波形更加平滑。假设被滤除信号均为噪声信号，对比两图中信号的信噪比，可以发现信噪比提升了22%

说明谐波窗函数法可以通过限定更窄的频带宽度，实现分析频段的准确定位，提高分解重构后信号的质量；在信号分解过程中滤除了更多的噪声信号(特别是50 Hz噪声)，省去了信号分析前对信号进行滤波预处理的工序，提高了分析效率；同时，由于滤波功能的实现，使得信号失真程度进一步降低，信噪比得到了提升。

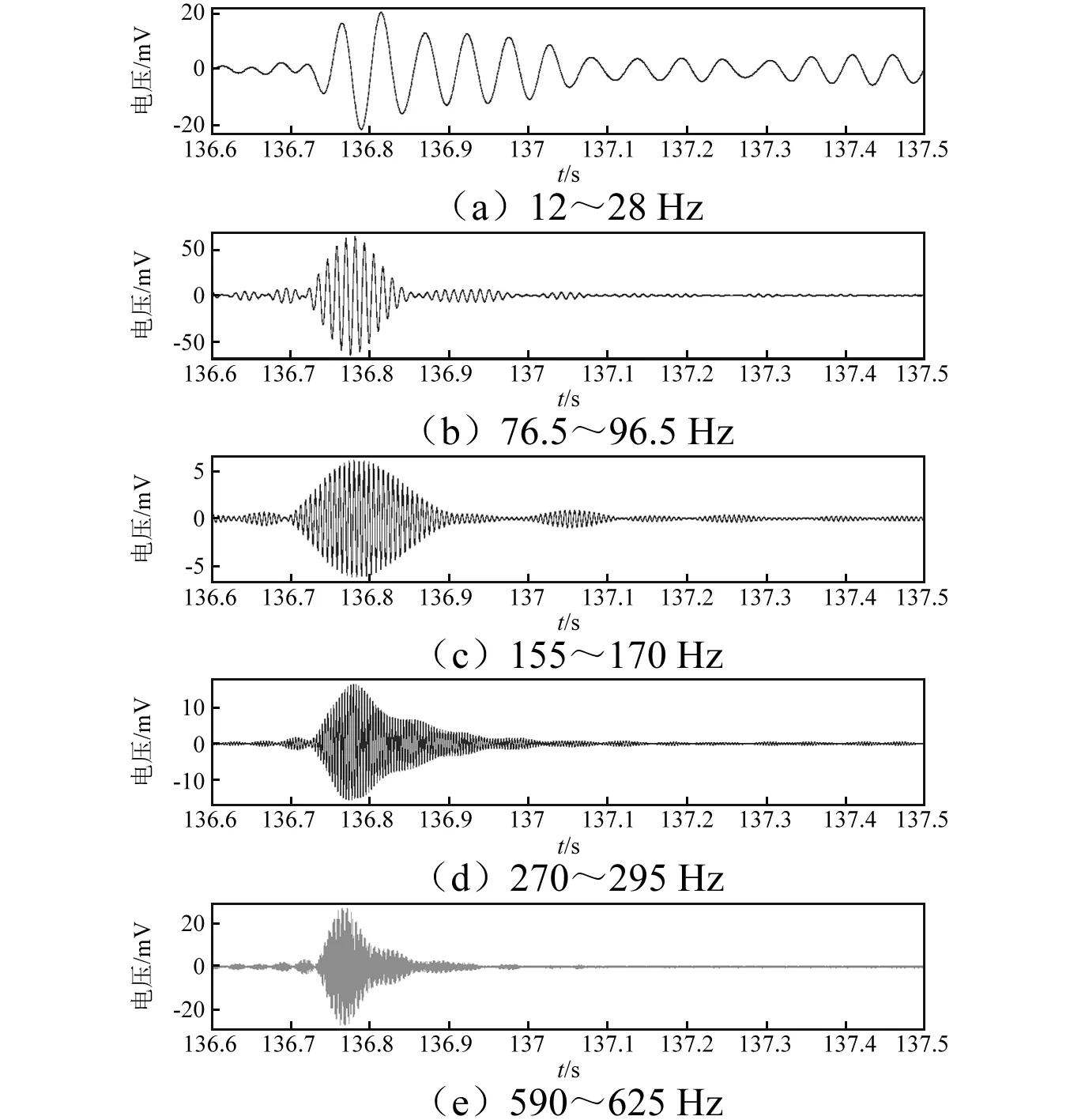
图9 五阶振动信号提取结果Fig.9 Five order Extracted signals

图9为5阶信号分解重构后的时域信号。从图中可以看出，各阶信号均成功的从原始信号被提取出来，且失真小、无相移。为后续的损伤检测分析提供了高质量的基础数据。

4 结 论

文本利用基于小波变换思想构建的谐波窗函数成功实现了对信号的分解与重构。通过对一钢筋混凝土梁实测振动信号的分析，得出以下结论：

(1)谐波窗函数法可以实现分析频段的自由划分，并提取出相应频段的信号。

(2)与传统小波变换相比，采用谐波窗函数法提取出的信号无数据量的损失，信号波形更加平滑，同时避免了因小波母函数选取不当带来的信号失真。

(3)由于谐波窗函数具有良好的“盒形”频谱，所以提取后信号无相移，表现出良好的锁相效果。

(4)在分解过程中，通过选择恰当的解频段，可以在提取信号的同时实现噪声的过滤。