浅析轮换对称性在积分计算中的应用

宋丽雅

长治学院师范分院 山西 长治 046000

1 轮换对称性在积分计算中的应用的意义

在定积分的计算中,我们常利用积分区间的对称性,结合被积函数的奇偶性,可以极大地简化计算的过程.那么,在重积分的计算中,类似地,我们可以利用积分区域的对称性与被积函数的奇偶性使计算更为简便.相应地,我们还可以发现,在曲线积分中也有这样的结果。

在解决实际问题的过程中,我们不难发现,积分区域的高度对称性实际上表明了变量X、Y、Z之间的某种可相互替代性,这便是轮换性.一般来说,先使用轮换性简化被积函数或使其形式易于化简,之后再利用对称性来解决问题,可以极大地减小我们在解决问题中的工作量.,提高解题效率,因此进一步加强对其的研究非常有必要。

2 轮换对称性在积分计算中的应用

2.1 二重积分的轮换对称性

平面区域D,具有轮换对称性,即若点(x,y)∈D,则(y,x)∈D.在平面直角坐标系中,区域D具有轮换对称性,直观表现为区域D关于直线y＝x对称。

例1设f(x)在[a,b]上连续,且f(x)＞0,平面区域D:a≤x≤b,a≤y≤b,证明:

例2设D:x2＋y2≤1,f(x,y)在D上连续,求cos2y)dxdy.所以

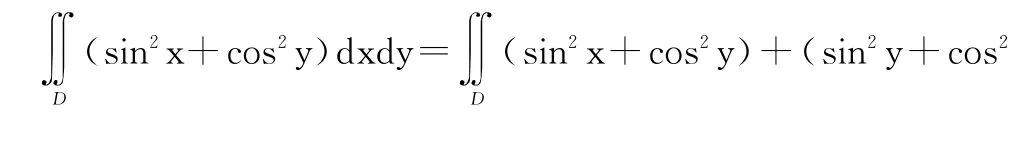
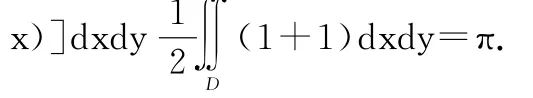
2.2 三重积分的轮换对称性

空间区域Ω,具有轮换对称性,即若点(x,y,z)∈Ω,则(y,z,x)∈Ω,且(z,x,y)∈Ω.在空间直角坐标系中,Ω具有轮换对称性,直观表现为Ω对三个坐标轴的相对位置是等同的。如Ω1:x2＋y2＋z2≤1和Ω2:(x－1)2＋(y－1)2＋(z－1)2≤2均具有轮换对称性。

2.3 曲线积分的对称性

设f(x,y)在曲线L上连续,其中L为平面上可求长度的曲线段,当积分弧段关于x轴对称,记L＝L1∪L1,且L1、L1关于x轴对称,

如果f(x,－y)＝－f(x,y),则

类似也有积分弧段关于y轴对称的结论.但积分弧段关于原点对称或轮换对称性的问题,以及类似结论在空间第一类曲线积分运算中也经常出现,我们有以下结论:

(1)设f(x,y)在曲线L上连续,当积分弧段关于原点对称,记L＝L1∪L2,且L1、L2关于原点对称,

如果f(－x,－y)＝－f(x,y),则∫Lf(x,y)ds＝0;如果f(－x,－y)＝f(x,y),则

(2)设f(x,y)在曲线上连续,当积分弧段关于坐标x,y具有轮换对称性,则

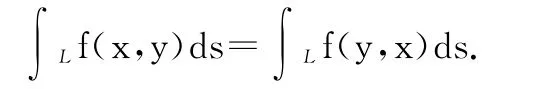
(3)设ff(x,y,Z)在空间曲线Γ上连续,其中Γ为空间上可求长度的曲线段,当积分弧段Γ关于y Oz坐标面对称,记Γ1,Γ2分别为Γ在y Oz坐标面的前半部分(x＞0)和后半部分(x＜0),

如果f(－x,y,z)＝－f(x,y,z),

类似也有积分弧段Γ关于zOx、x Oy坐标面对称的结论.

2.4 曲面积分的对称性

设函数f(x,y,z)为有界光滑或分片光滑曲面∑上的连续函数,∑关于坐标面x＝0对称,如果f(－x,y,z)＝－f(x,y,z),则

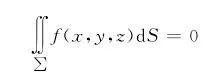
如果f(－x,y,z)＝f(x,y,z),则

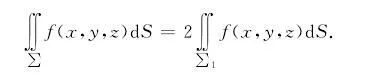
(其中∑1＝(x,y,z)∈∑x≥{0}).

如∑关于坐标面y＝0,z＝0对称,有类似的结论.而如果∑对坐标x,y,z具有轮换对称性,则

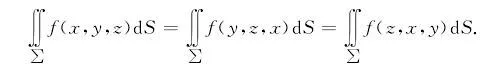
以上是第一类曲面积分,这些结论我们一般都比较熟悉,而对于第二类曲面积分,我们先给出以下定义:

定义2 指定了曲面的侧的曲面称为有向曲面,根据曲面上点(x,y,z)处的法向量的方向余弦的正负,我们定义了曲面的前侧(cosα＞0),后侧(cosα＜0),右侧(cosβ＞0),左侧(cosβ＜0),上侧(cosγ＞0),下侧(cosγ＜0)等.

总之,在定积分的计算中,我们常利用积分区间的对称性,结合被积函数的奇偶性,可以极大地简化计算的过程,因此进一步加强对其的研究非常有必要。