跳频信号2D-DOA高精度估计算法
胡政权,刘 毓,牛晓伟
(重庆三峡学院电子与信息工程学院,重庆 404100)
0 引言
跳频通信因为其良好的抗干扰性能、较低的被截获概率和较强的多址组网能力而被广泛的应用在军事和民用通信领域。但是随着通信电磁环境的日渐复杂,如何有效地进行跳频通信的侦察与抗干扰也愈加困难[1-3]。跳频信号的参数估计是通信对抗的基础,是最重要的一环。
目前大多关于跳频信号参数估计集中在跳频信号的时域和频域参数估计,较少的研究着眼于空域参数。信号的波达方向估计中基于子空间分解的多重信号分类算法和旋转不变技术(Estimation of Signal Parameter via Rotation Invariance Technique, ESPRIT)被广泛应用[4]。文献[5-6]提出一种空时频分析和MUSIC算法相结合的跳频信号一维波达方向估计算法,该算法简单易于实现,但是低信噪比和小快拍数时算法性能下降严重。文献[7]提出一种基于SCMUSIC&STFD算法的跳频信号DOA估计算法,这种算法主要解决了MUSIC算法复杂度高的问题,但是没有解决低信噪比下算法的估计精度问题。文献[8]提出一种基于基于ESPRIT算法的跳频信号DOA估计算法,大大降低了算法复杂度,但是这种算法对阵列要求较高,限制了算法应用条件。文献[5-8]所提算法仅局限于跳频信号一维波达方向的估计,无法实现跳频信号目标的三维定位。文献[9-10]提出一种基于空间极化时频分布的跳频信号2D-DOA估计算法,该算法本质上还是运用了ESPRIT算法来实现跳频信号的二维波达方向的估计,算法的信噪比适应能力较差。
目前现有关于跳频信号二维波达方向估计研究中,存在低信噪比和小快拍数下算法性能下降严重问题。本文针对此问题提出一种基于二阶偏导MUSIC跳频信号2D-DOA高精度估计算法。该算法运用传统MUSIC算法估计波达方向构造的空间谱函数极大值点处存在方位角和俯仰角的二阶偏导,并且二阶偏导小于零的特性,通过对跳频信号的方位角和俯仰角求二阶偏导构造新的MUSIC算法空间谱函数,将传统极值谱峰搜索转化为负向谱峰搜索。
1 跳频信号阵列快拍模型与空间谱函数构建
假设跳频信号接收机在观测时间ΔT和观测频段ΔW内接收到的跳频信号y(t)为:
(1)
式(1)中,sn(t)表示第n个跳频信号;v(t)表示均值为零,方差为σ2的高斯白噪声。
假设观测时间内有K个跳频信号,第k(k=1,…,K)个完整跳的中心频率为fnk,初相为φnk,最开始非完整跳的持续时间为Δtn0,中心频率为fn0,初相为φn0,则sn(t)可表示为[11]:
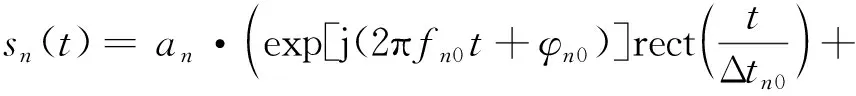
(2)
式(2)中,an表示第n个跳频信号的基带复包络;rect(t)表示单位矩形脉冲函数。
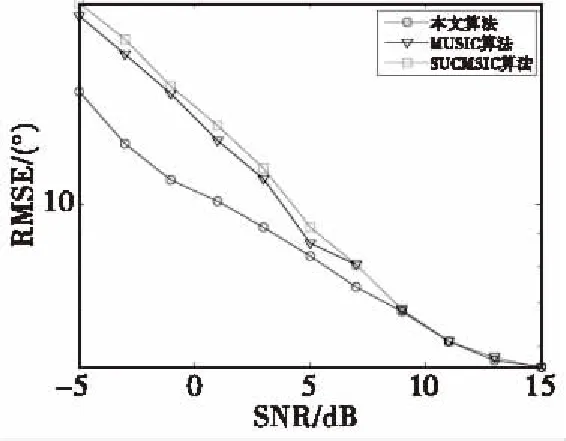
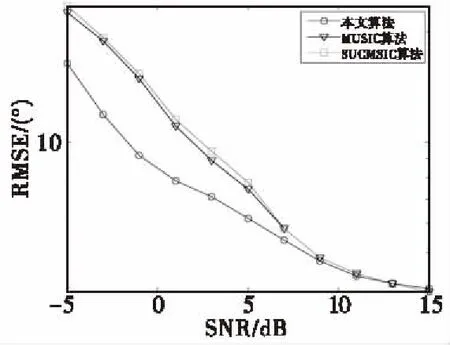
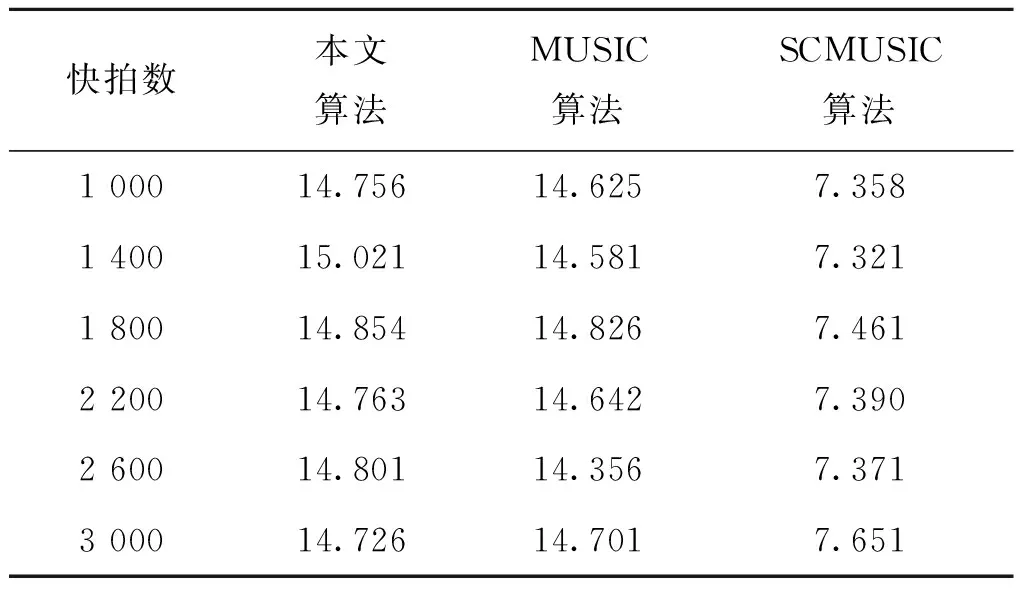
假设有N个远场跳频信号以二维方向角度(θk,φk)(θk和φk分别代表第k个跳频信号的的方位角和俯仰角)入射到如图1所示的M元双均匀平行线阵上。其中,阵元间距为d1,两个阵列的间距为d2,且满足max(d1,d2) 图1 信号入射示意Fig.1 Signal incident diagram 假设跳频信号的波长为λ,则阵列1对入射信源S的导向矢量aS1(θ,φ)为: aS1(θ,φ)=[1,e-j2πd1sinθcosφ/λ,…, (3) 阵列2与阵列1的导向矢量的差别是由两个阵列之间的间距d2引起的,阵列2的导向矢量aS2(θ,φ)可以表示为: aS2(θ,φ)=[1,e-j2π(d1sinθcosφ+d2sinθsinφ)/λ,…, (4) 因此,双均匀线阵对入射信源S的导向矢量a(θ,φ)可以表示为: (5) 根据式(5)可以得到阵列流型矩阵为: A=[a1(θ,φ),a2(θ,φ),…,aN(θ,φ)] (6) 假设双均匀平行线阵接收到的信号矢量X(t)=[x1(t),x2(t),…,xM(t)]T,跳频信号的信源矢量S(t)=[s1(t),s2(t),…sN(t)]T,阵列噪声信号矢量S(t)=[s1(t),s2(t),…sN(t)]T,则跳频信号的阵列快拍模型可以表示为: X(t)=Y(t)+N(t)=AS(t)+N(t) (7) 跳频信号的载频是随机跳变的,如果直接采用平稳信号协方差矩阵求解法会导致跳频信号的流型矩阵也是随机变化的。文献[12]利用跳频信号的时频图将跳频信号分解为一个个独立的跳,这样可以将跳频信号简化为频率固定的窄带信号。跳频信号x(t)的空时频分布可以表示为: (8) 式(8)中,[DXX(t,f)]ij=Dxixj(t,f) 为跳频信号之间的互时频分布。 因此,跳频信号的时频域协方差矩阵可以表示为: E[DXX(t,f)]=E[DYY(t,f)]+E[DNN(t,f)]= (9) 根据式(9)对跳频信号的阵列协方差矩阵E[DXX(t,f)]进行特征值分解可得: (10) 式(10)中,US为K个大特征值对应的特征向量张成的信号子空间,UN为(NM-K)个小特征值对应的特征向量张成的噪声子空间,H为E[DXX(t,f)]特征值组成的对角矩阵。 根据正交子空间原理,由噪声子空间UN构造的MUSIC算法空间谱函数可以表示为: (11) 根据式(11)进行谱峰搜索,谱峰位置对应的(θ,φ)即为跳频信号的二维入射角度。根据空间谱函数进行谱峰搜索想要获得较高的估计精度,需要信噪比足够高、快拍数足够大、搜索精度足够大。与此同时,快拍数的增加会大大增加算法的复杂度,而且实际应用中的信噪比无法满足MUSIC算法精确估计的标准。 假设跳频信号方位角θ的角度范围为Rθ,谱峰搜索的步长为Δθ,则方位角的搜索次数L=Rθ/Δθ;俯仰角φ的角度范围为Rφ,谱峰搜索的步长为Δφ,则方位角的搜索次数K=Rφ/Δφ。因此,空间谱函数P可以进一步表示为: (12) 根据式(12),将空间谱函数P简化为: (13) 根据式(13)可知,给定一个(i,j),i=1,2,…,L,j=1,2,…,K,都存在一个固定的数值pij与之对应。假定方位角θ∈D1={θ1,θ2,…θL},Δθ=θi+1-θi,φ∈D2={φ1,φ2,…φL},Δφ=φj+1-φj,则pij可以进一步表示为: pij=f(θi,φj) (14) (15) 式(15)中,∑(·)表示在θl点的邻域内求和。因为0≤|θi-θl|≤n,(n=1,2,…,L),所以式(15)可以进一步表示为: (16) (17) (18) (19) 由于空间谱函数在极大值点的二阶导数会在方位角和俯仰角的位置形成尖锐的负向谱峰,说明只有小于零的二阶偏导值对DOA的计算是有用的,因此可以将二阶偏导函数中大于零的数值去除。则式(17)和式(19)可以简化为: (20) (21) 空间谱函数对方位角θ和俯仰角φ求二阶偏导时是相互独立的,因此可以定义新的空间谱函数的二阶导数p″为: (22) 根据式(22)进行负向谱峰搜索得到的负峰值点对应的方位角和俯仰角即为跳频信号的2D-DOA参数。根据式(22)进行负向谱峰搜索也相当于原空间谱函数进行极大值搜索,可以准确的得到跳频信号的2D-DOA参数。 根据上述的理论推导,基于二阶偏导MUSIC跳频信号2D-DOA高精度估计算法的步骤可以归纳为: 步骤1 由阵列接收到的数据,根据式(7)构建跳频信号阵列的快拍矢量模型; 步骤2 根据式(10)对跳频信号的协方差矩阵E[DXX(t,f)]进行特征值分解得到噪声子空间UN; 步骤3 利用噪声子空间,根据式(11)构造跳频信号2D-DOA估计的空间谱函数; 步骤5 根据式(22)得到跳频信号2D-DOA估计的新的空间谱函数p″; 步骤6 利用p″进行负向谱峰搜索,得到的负峰值点即为跳频信号的方位角和俯仰角参数。 假设接收阵列的阵元间距d1=10 m,阵列间距d2=30 m;入射信号为3个跳周期均为10 μs的跳频信号FH1、FH2、FH3,采样率为100 MHz;其2D-DOA的方位角和俯仰角参数(θ,φ)分别为(23°,80°),(39°,69°),(42°,65°)。 本文的仿真结果均为200次蒙特卡洛实验结果,用均方根误差RMSE来衡量算法估计精度,定义跳频信号方位角和俯仰角的RMSE为: (23) 仿真条件:阵列x轴方向和y轴方向的阵元数均为5个,每跳的快拍数均为2 000,信噪比从-5 dB以2 dB为步进递增至15 dB。本文算法、MUSIC算法和SCMUSIC算法的方位角和俯仰角的RMSE曲线如图2和图3所示。 图2 实验1方位角RMSE曲线Fig.2 Azimuth RMSE curve of experiment 1 图3 实验1俯仰角RMSE曲线Fig.3 Pitching angle RMSE curve of experiment 1 从实验1的仿真结果可以看出,随着信噪比的增加,本文算法、传统MUSIC算法和SCMUSIC算法的方位角和俯仰角的估计精度都逐渐增加;信噪比小于5 dB时,本文算法的方位角和俯仰角估计精度远高于MUSIC算法和SCMUSIC算法,SCMUSIC算法的估计精度略低于MUSIC算法,但是随着信噪比的增加三种算法的估计精度越来接近,信噪比达到9 dB左右时,三种算法的估计精度几乎相同。 仿真条件:阵列x轴方向和y轴方向的阵元数均为5个,信噪比为9 dB,每跳的快拍数从1 000以200为步进递增到2 000。本文算法、MUSIC算法和SCMUSIC算法的方位角和俯仰角的RMSE曲线如图4和图5所示。 图4 实验2方位角RMSE曲线Fig.4 Azimuth RMSE curve of experiment 2 图5 实验2俯仰角RMSE曲线Fig.5 Pitching angle RMSE curve of experiment 2 从实验2的仿真结果可以看出,随着快拍数的增加,本文算法、MUSIC算法和SCMUSIC算法的方位角和俯仰角的估计均方根误差都逐渐减小;快拍数小于2 200时,本文算法的估计精度要远大于MUSIC算法和SCMUSIC算法,MUSIC算法的估计性能略高于SCMUSIC算法;快拍数大于2 200时,随着快拍数的增加三种算法的估计性能逐渐接近。 仿真条件:阵列x轴方向和y轴方向的阵元数均为5个,信噪比为9 dB。快拍数为1 000,1 400,1 800,2 200,2 600,3 000时本文算法、MUSIC算法和SCMUSIC算法的2D-DOA估计时间如表1所示(时间为200次蒙特卡洛实验平均时间)。 表1 2D-DOA估计时间对比 从表1的实验结果可以看出,不同的快拍数下,本文算法2D-DOA所需仿真时间略大于MUSIC算法,但是时间增加不显著。SCMUSIC算法的计算时间约为本文算法和MUSIC算法的一半左右,造成这种现象的主要原因是,本文算法相比较MUSIC算法,虽然单次谱峰搜索的次数减少,但是需要两次搜索;SCMUSIC只需要在半谱内进行角度搜索。 本文提出了一种基于二阶偏导MUSIC跳频信号2D-DOA高精度估计算法。该算法根据跳频信号2D-DOA估计空间谱函数的特性,利用离散函数的二阶偏导特性,重建新的空间谱函数,将原谱峰搜索转化为负向谱峰搜索。理论分析仿真结果表明,所提算法相比较MUSIC算法在没有显著提高算法复杂度的条件下,提高了低信噪比和小快拍数下的估计精度;相比较SCMUSIC算法大大改善了在低信噪比和小快拍数条件下的估计性能。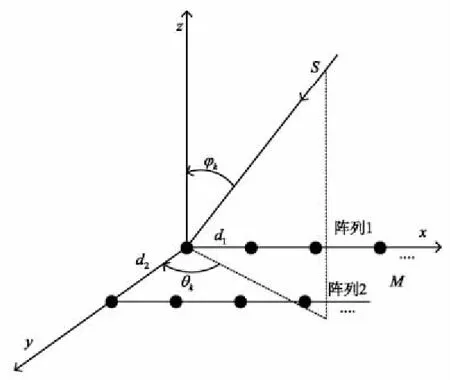
e-j2π(M-1)d1sinθcosφ/λ]T
e-j2π[(M-1)d1sinθcosφ+d2sinθsinφ]/λ]T
ADSS(t,f)AH+E[DNN(t,f)]2 基于二阶偏导MUSIC估计2D-DOA

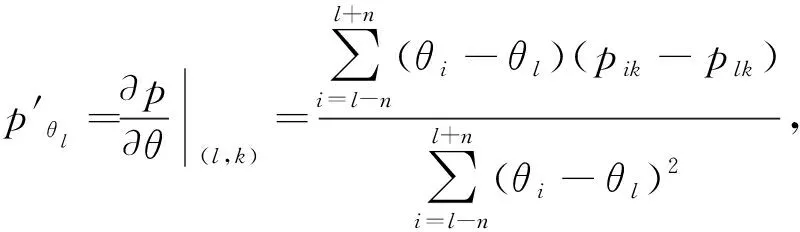

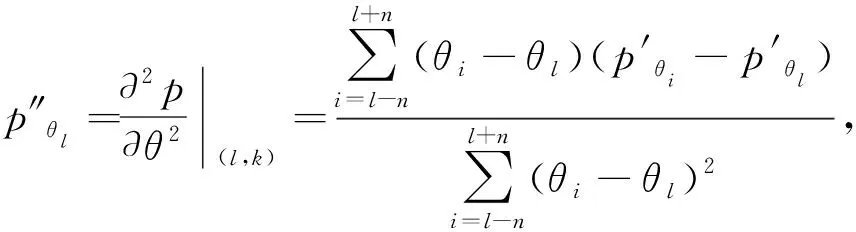

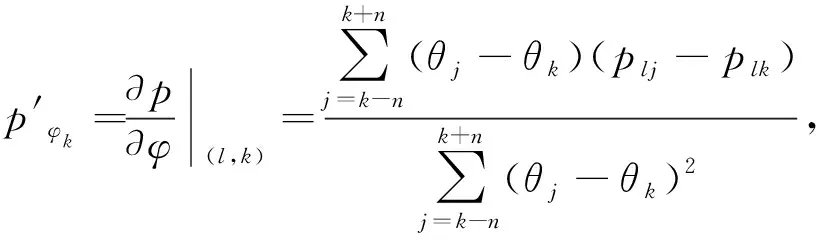


3 仿真与分析

3.1 实验1
3.2 实验2


3.3 实验3
4 总结

