Zero-Quantum Homonuclear Recoupling Symmetry Sequences in Solid-State Fast MAS NMR Spectroscopy

Yi Ji , Lixin Liang , Changmiao Guo , Xinhe Bao , Tatyana Polenova ,4, Guangjin Hou ,＊ State Key Laboratory of Catalysis, Dalian Institute of Chemical Physics, Chinese Academy of Sciences, Dalian 602,

Liaoning Province, P. R. China.

2 University of Chinese Academy of Sciences, Beijing 100049, P. R. China.

3 Department of Chemistry and Biochemistry, University of Delaware, Newark, Delaware 19716, United States.

4 Pittsburgh Center for HIV Protein Interactions, University of Pittsburgh School of Medicine, Pittsburgh, PA 15261, United States.

Abstract:The considerable demand of robust solid-state nuclear magnetic resonance (NMR) sequences has been met by the development in solid-state NMR hardware and probe design,particularly for fast magic angle spinning (MAS). Fast MAS enhances spectral resolution, however, it makes many conventional methods unusable because of the need of significantly high radiofrequency (RF)field strength and the intrinsic inefficiencies under such condition.Dipolar-based homonuclear recoupling sequences are widely used for structural analysis, and radio-frequency driven recoupling (RFDR) is one of the most popular zero-quantum (ZQ) homonuclear recoupling sequence. Previous studies demonstrated that RFDR efficiency strongly depends on factors such as MAS frequency, resonance offset,RF field inhomogeneity, and chemical shift anisotropy (CSA). To alleviate these dependencies, different RFDR phase cycles have been proposed. To completely understand the principle of ZQ recoupling sequences and achieve uniform broadband homonuclear recoupling under fast MAS conditions, we herein utilize the theory of symmetry sequences and propose a series of RNN1 (N ≥ 4, N is even) sequences with various phase cycles under both moderate and fast MAS conditions. We simulated the influence of MAS rate, resonance offset,RF field strength, RF mismatch, and heteronuclear decoupling on ZQ homonuclear polarization transfer efficiency. We verified the ZQ dipolar recoupling efficiencies of various RN symmetry sequences using U-13C, 15N-labeled L-histidine and microcrystalline U-13C, 15N-labeled dynein light chain (LC8) protein. The basic R4 sequence showed the worst broadband ZQ polarization transfer performance theoretically and experimentally, while the basic R6 sequence could efficiently achieve ZQ dipolar recoupling within moderate bandwidth. Under low to moderate MAS conditions, high-power 1H decoupling could considerably enhance the polarization transfer efficiency, while homonuclear recoupling sans heteronuclear decoupling is recommended under fast MAS conditions. Super phase cycling enhanced ZQ polarization transfer efficiency and bandwidth and resulted in significantly reduced sensitivity to RF mismatch. RNixy3 and RNixy4 sequences with 6＊N and 8＊N phase cycling steps, respectively, were preferred. The R4ixy3 sequence with fewer phase cycling steps showed comparable, or even slightly better, performance to the R4ixy4 sequence. As shown in the simulations,by choosing proper RF field strengths, 1.5＊ωr ＜ ω1 ＜ 3＊ωr, uniform broadband ZQ recoupling with R4ixy3 or R4ixy4 sequences could be achieved under fast MAS conditions, which would be significant for the accurate determination of spatial proximities and internuclear distances. By prolonging the mixing time, the RN ZQ scheme could provide more cross peaks,where medium- to long-range spatial correlations could be included; these correlations are essential for structural determination in complex systems.

Key Words:Symmetry-based pulse sequence;Zero-quantum homonuclear recoupling;RFDR;Super phase cycling;Fast MAS;Solid-state NMR

1 Introduction

Breakthroughs in NMR hardware and probe design technology in the recent decade have dramatically accelerated the solid-state NMR applications to the problems in inorganic materials, organic chemistry, polymers, biology, and medicine.One of the most promising recent developments is in the ultrafast MAS probes, where frequencies up to 140 kHz are accessible now1,2. Under such conditions, the spectral resolution and sensitivity can be enhanced greatly due to the efficient suppression on1H–1H homonuclear and1H–X heteronuclear dipolar couplings, without or with RF field irradiation using very low radiofrequency (RF) field strengths. Under such conditions,proton-detected NMR experiments can be performed in fully protonated solids3,4, where the sensitivity is improved dramatically and additional information about proton chemical shifts can be incorporated into the spectral analysis. At the same time, technical advances in fast MAS also bring new challenges to the NMR researchers5. At fast MAS, the conventional spin diffusion methods, proton-driven spin diffusion (PDSD)6and dipolar assisted rotational resonance (DARR)7, no longer work.Several solid-state NMR laboratories including us have contributed to designing the novel types of spin diffusion pulse sequences, using amplitude-modulated, phase-modulated, or both amplitude- and phase-modulated RF pulses during the mixing time8–14. In these sequences, the polarization transfer efficiency is enhanced when the broadened second-order rotational resonance condition, (ω1± nωr− ΚscωDD) < Δωiso<(ω1 ± nωr + ΔΚscωDD), is attained. Although the broadband homonuclear recoupling can be obtained when implementing appropriate phase cycle on the applied RF pulses, including CORD9, PARIS-xy12, and SHANGHAI+13etc., the efficiency of the polarization transfer is very limited due to the intrinsic second-order rotational resonance recoupling. In addition, it can be difficult to extract the internuclear distance information directly as the cross peak intensity varies due to the complexity of the proton networks. Nevertheless, attaining accurate distance information from spin diffusion type polarization transfers is of great interest for structural analysis15–18.

Besides the proton-assisted spin diffusion schemes, the firstorder recoupling schemes, such as SPC-519, CMpRR20, radiofrequency driven recoupling (RFDR)21, finite-pulse radiofrequency driven recoupling (fpRFDR)22,23and dipolar recoupling enhanced by amplitude modulation (DREAM)24,have been successfully applied for the determination of the spatial proximity of homonuclear spin pairs under fast-toultrafast MAS conditions. These sequences are mainly suitable for the observation of short-range correlations since most of them suffer from the dipolar truncation effect25. Compared to the spin diffusion based experiments, these first-order recoupling schemes allow for much more efficient polarization transfer between the recoupled spin pairs, and usually the spatial proximity can be obtained in only a few milliseconds, although the transfer efficiency depends strongly on the pulse imperfections such as the resonance offset and RF field inhomogeneity. Recoupling scheme named CORD-RFDR10which combines CORDxy4 and fpRFDRxy16 schemes has proven to be efficient for dipolar recoupling of both long- and shortrange correlations in a single measurement. Even though CORDRFDR is capable of yielding13C–13C correlations corresponding to distances as long as 7–9 Å (1 Å = 0.1 nm), the recoupling ability for atoms separated by several bonds is still based on empirical fitting and can in practice be only achieved semiquantitatively.

Among first-order recoupling techniques, the homonuclear RFDR has been widely studied and used for establishing spatial proximities due to its simplicity of implementation. However,because of its high sensitivity to the experimental or system parameters such as MAS frequency, resonance offset, RF field inhomogeneity, and chemical shift anisotropy (CSA), the applications of RFDR mostly focus on establishing correlations between spatially proximal sites, but not on the determination of internuclear distances. In order to overcome the limitations of RFDR or fpRFDR scheme, previous studies have examined the effects of super phase cycling, and it was shown that these could improve the excitation bandwidth and also the robustness with respect to pulse imperfections4,26,27,28.

In this work, we present a family of RNN1-symmetry-based zero-quantum (ZQ) pulse schemes with various phase cycles that are well suited for low-to-fast MAS conditions. The performance of these first-order recoupling schemes is evaluated theoretically and experimentally.

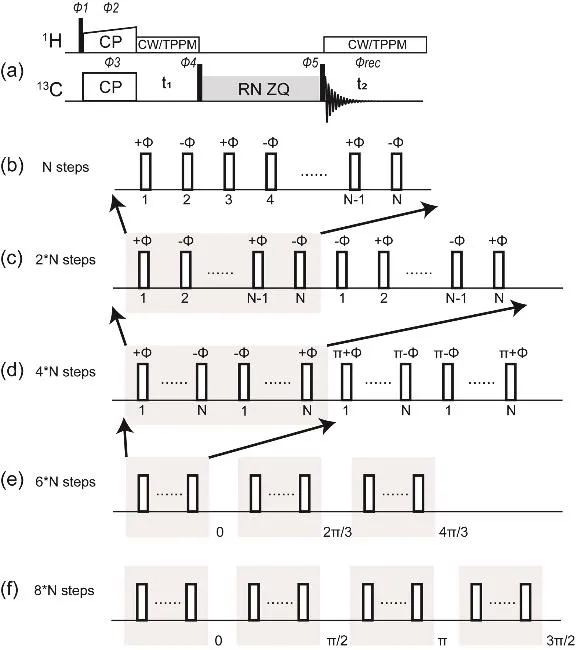
Fig. 1 (a) Pulse sequence for zero-quantum homonuclear correlation spectroscopy under fast or ultrafast MAS conditions; no 1H decoupling was applied during the mixing period. Various RNN1 symmetry sequences can be applied during the mixing time, including (b) basic RNnv (named RN), super phase cycled (c) RNnv RNn−v (named RNi), (d)[RNnv RNn−v]0[RNnv RNn−v]180 (named RNixix), (e) [RNnv RNn−v]0[RNnv RNn−v]120[RNnv RNn−v]240 (named RNixy3), (f) [RNnv RNn−v]0[RNnv RNn−v]90[RNnv RNn−v]180[RNnv RNn−v]270 (named RNixy4) symmetry sequences. Phase cycling for pulses shown in Fig. 1a: Φ1 = 1, 3; Φ2 = 0;Φ3 = 0, 0, 2, 2; Φ4 = 1, 1, 1, 1, 3, 3, 3, 3; Φ5 = 0, 0, 0, 0, 0, 0, 0, 0, 2, 2,2, 2, 2, 2, 2, 2; Φrec = 1, 3, 3, 1, 3, 1, 1, 3, 3, 1, 1, 3, 1, 3, 3, 1.

2 Experimental

2.1 Materials

The preparation of the samples used in this work was reported previously8. U-13C,15N-labeled L-histidine was purchased from Cambridge Isotope Laboratory. Histidine sample was doped with 0.1% (mole fraction) CuCl2and re-crystallized before packing into MAS rotor. U-13C,15N-enriched dynein light chain protein (LC8) was expressed in E. coli and purified. LC8 was prepared by controlled precipitation, EG-3350 and LC8 were separately dissolved in 10 mmol·L−1MES buffer (10 mmol·L−1MgCl2, pH 6.0) and doped with 50 mmol·L−1EDTA-Cu(II).Subsequently, a solution of 30% PEG-3350 was slowly added to the solution of 11 mg of LC8 (30 mg·L−1).

2.2 Pulse sequence

The pulse sequence for the RNN1-symmetry-based zeroquantum homonuclear correlation spectroscopy is shown in Fig.1a. During the mixing time,1H RF field irradiation decoupling sequence can be applied if desired. Usually1H decoupling during the mixing period is not required for fast or ultrafast MAS conditions (ωr> 35 kHz), while high power continuous wave(CW)1H decoupling is needed for slow-to-moderate MAS conditions (ωr< 30 kHz).13C transverse magnetization is prepared by cross polarization and evolves in t1. A 90° pulse on the13C channel is applied followed by a RNN1-based zeroquantum recoupling sequence, after which a second 90° pulse is applied on the13C channel for the signal detection in the direct dimension. Various RNN1symmetry recoupling schemes with different phase cycles can be applied on13C during the mixing period, as shown in Fig. 1b–f. (We also tested RNxy3sequences corresponding to [RNnv]0[RNnv]120[RNnv]240which are not shown in Fig. 1, where phase cycling is used with phase increment of 120°, but without 180° phase inversion.) For all of these RNN1-based sequences, a finite-width π pulse is applied in the middle of every rotor period. The pulse sequences are called windowless RN when there are no delays between two adjacent π pulses,while delays placed among the π pulses result in windowed RN sequences. The window fraction represents the ratio between the length of the delay and the π pulse. For a typical case, at a MAS rate of 40 kHz, the13C RF field strength is 20 kHz (windowless)and 60 kHz for the 66.7% window fraction. Amplitude- or phase-modulated pulse or composite pulses might also be used to replace the π pulse23,26,29,30, as implemented in POST-RN sequences. In the present work we restrict the discussion to the RN sequences with basic π pulses.

2.3 Numerical simulations

All numerical simulations were performed using SIMPSON31.168 REPULSION angles (α, β) and 32 γ were used to get a powder average, unless noted otherwise. The model spin system(C2H2) employed in the simulations was taken from the solidstate NMR structure of N-f-MLF-OH tripeptide (PDB ID:1Q7O), where CSA of13C and all dipolar couplings were included, but J coupling was ignored for its negligible size. All other parameters used in the simulations were the same as in the corresponding NMR experiments8. The proton resonance frequency was always set to 600 MHz in all simulations and the mixing time was 2.4 ms at 40 kHz MAS and 4.8 ms at 20 kHz MAS. The start operator was I1zfor C1and the detect operator was I2zfor C2. The ZQ polarization transfer efficiency was determined as two times of I2z(detect)/I1z(start).

2.4 NMR spectroscopy

All NMR experiments were conducted on a Varian InfinityPlus solid-state NMR spectrometer operating at a Larmor frequency of 599.8 MHz for1H and 150.8 MHz for13C, and a 1.8 mm MAS triple-resonance HXY probe developed in the Samoson Laboratory was used. The MAS frequency was either 40 kHz for fast MAS condition or 25 kHz for moderate MAS condition, and controlled to within ±5 Hz using a Varian MAS controller. To reduce the sample heating caused by MAS rotation, nitrogen gas was used for cooling, resulting in a final sample temperature of 20 °C for His sample, and 0 °C for LC8 protein.

2D NMR experiments were collected using the pulse scheme shown in Fig. 1a. RNN1based ZQ recoupling irradiations with different phase cycles were applied during the mixing period, to drive the polarization transfer between the neighboring spin pairs, and a series of corresponding 2D NMR spectra were recorded. For both His and LC8, the1H-13C cross polarization(CP) transfer was performed with a linear amplitude ramp (90%–110%) on1H, and the center of the ramp was matched to the first spinning sideband of the Hartmann-Hahn ZQ matching conditions. The typical 90° pulse lengths were 2.5 and 3.5 μs for1H and13C, respectively. Low power TPPM1H decoupling with an RF field strength of 11 kHz was applied during t1and t2dimensions. All NMR data were processed with NMRPipe in a Mac environment using a standard protocol including apodization, zero-filling, Fourier transform, phase correction and baseline correction in both dimensions.

3 Results and discussion

3.1 Zero-quantum homonuclear dipolar recoupling RN symmetry sequences

According to the symmetry-based pulse sequence theory, all of the RNN1(N ≥ 4, N is even) symmetries could exclusively(ignoring J coupling) recouple homonuclear dipolar coupling of the (l, m, λ, μ) = (2, ±1, 2, 0) and (2, ±2, 2, 0) terms in the first order average Hamiltonian with the same scaling factor of 0.216 and 0, respectively, when applying windowless π pulses23,30.SEDRA32, RFDR21and fpRFDR22could be thought as R441-based sequences with windowed π pulses, which makes R441most prevalent for homonuclear first-order recoupling among all RNN1type symmetries.

Despite being widely used, the basic R441sequence with phase cycle of x, y, x, y (also called as RFDR(XY4)) does not work well because of the interferences from isotropic shift, CSA and heteronuclear dipolar coupling. Moreover, the transfer efficiency could be affected by the huge amount of terms recoupled in the second order average Hamiltonian. Super-phase cycling has been used to suppress the influence from these higher order terms. Briefly, the phase inversion R441R44−1sequence with 8-step phase cycle of x, y, x, y, y, x, y, x, (also called as RFDR(XY8)), could remove the zero-quantum (ZQ, λ1=λ2and µ1+ µ2= 0) cross terms, and additional overall phase shift(XY16 and (XY8)41) could further remove the single-quantum(SQ, µ1 + µ2 = ±1) and double-quantum (DQ, µ1 + µ2 = ±2) cross terms for R441symmetry23,26,27.

Besides the R4 symmetry sequence, stricter symmetries like R661and R881can also be used for obtaining ZQ homonuclear recoupling. Note that the symmetry number is limited to less than 10 in our present work due to the increased number of phase steps required for the phase cycle. As shown in Table 1, there are fewer cross terms for homonuclear dipolar coupling (DD) ×chemical shift (isoCS or CSA) and DD × heteronuclear dipolar coupling (hetero-DD) in basic-R661and R881than in basic-R441.(Considering that ICcommutes with IH, cross terms for DD ×CSA and DD × hetero-DD are shown in the same column.)However, we also notice that all of the basic-RNN1sequences recouple large number of DD × DD terms (and other cross terms such as CSA × CSA) which could only be suppressed by super phase cycling. Even though a 32-steps super-phase cycle((XY8)41/R4ixy4) was proven to make fpRFDR more robust than a 16-steps cycle (XY16/R4ixix), a compromise between 16 and 32 steps exists. R4ixy3 sequence with an overall phase increments of 2π/3 (in place of the regular π or π/2), suggested in the previous reference23, could make the recoupling sequence shorter and comparable in robustness to R4ixy4. The detailed comparison of different RNN1-based sequences with various phase cycles contributes to screening the appropriate symmetry sequence for zero-quantum recoupling techniques under fast MAS conditions.

Table 1 Numbers of cross terms recoupled in the second-order average Hamiltonian for basic RNN1 sequences.

3.2 Broadband homonuclear recoupling for different RN sequences

Fig. 2 shows the simulated transfer efficiency plots for various RN symmetry sequences as a function of the difference in resonance frequencies for a C2H2 spin system. R441, R661and R881-type symmetry sequences with various super phase cycles were used. (R441, R661and R881are abbreviated as R4, R6 and R8 in the following discussion).13C RF field strength was chosen to be 60 kHz at a MAS frequency of 20 or 40 kHz. This choice is not optimal indeed, and higher RF field could lead to more broadbanded polarization transfer, as shown in Fig. 3 and Fig. 4. Such RF field strength cannot be accessible on most of commercial ultrafast MAS solid NMR probes, and therefore it would be helpful to compare the performance of RNN1-based sequences. Generally, high performance sequences with low power RF field requirements are usually desired for NMR experiments.

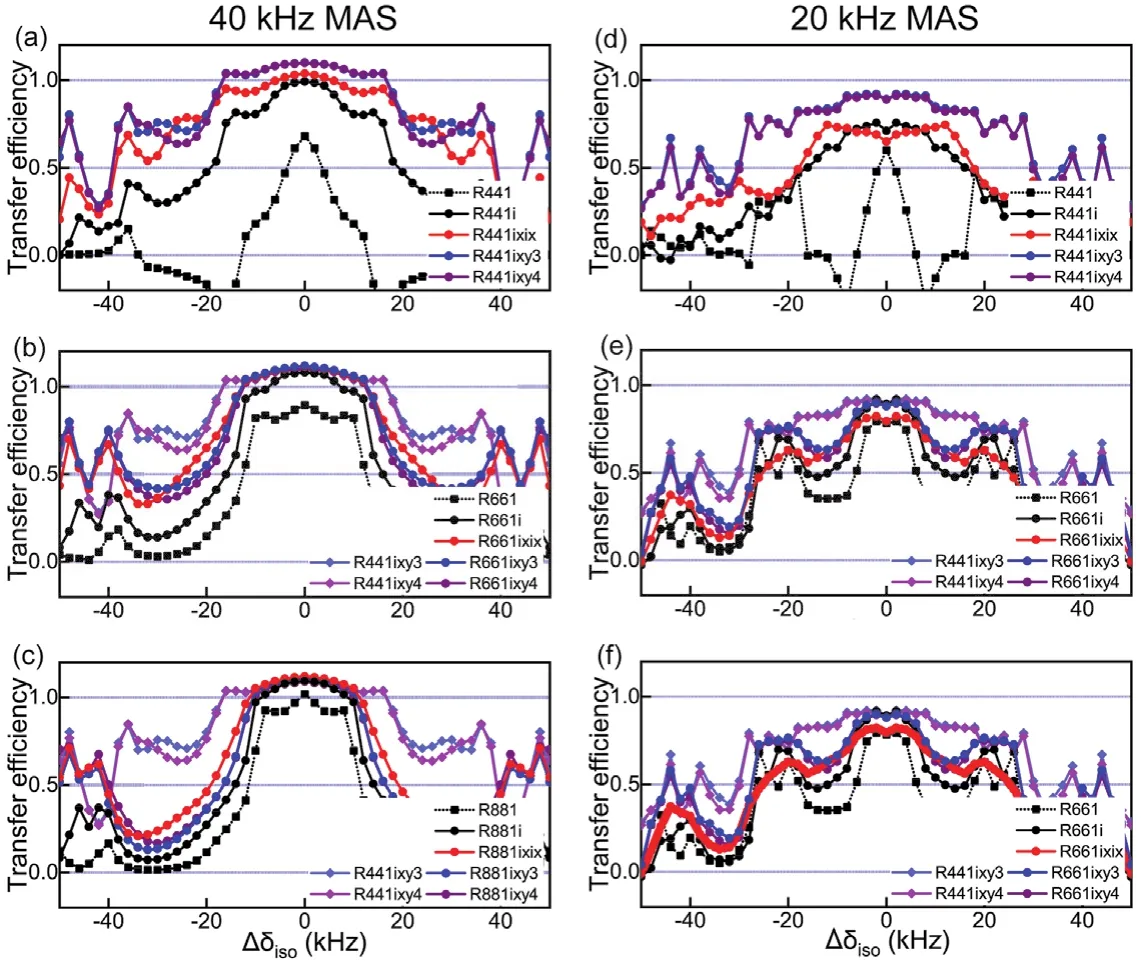
Fig. 2 Transfer efficiency plots of various RN-type symmetry sequences for ZQ recoupling as a function of frequency difference between spin pairs,Δδiso, at the MAS frequencies of 40 and 20 kHz. The mixing time is 2.4 ms for (a) R4, (b) R6, (c) R8-based sequences at the MAS frequency of 40 kHz and 4.8 ms for sequences (d) R4, (e) R6, (f) R8-based sequences at the MAS frequency of 20 kHz. No proton decoupling was applied during the mixing period. 13C RF field strength for π pulses applied in RN symmetry sequences was 60 kHz for the MAS frequencies of 40 and 20 kHz.

According to the results of our simulations shown in Fig. 2,complex phase cycling generally benefits the transfer efficiencies for all R4, R6 and R8 sequences. Basic R4 sequence shows the worst broadband ZQ polarization transfer ability,while basic R6 and R8 perform comparably to the versions with complex phase cycling steps, where broadband (up to +/−10 kHz) uniform transfer can be obtained by the basic R6 scheme with a 6-step phase cycle of π/6, −π/6, π/6, −π/6, π/6, −π/6. This behavior could be understood in light of the fact that basic R4 recouples too many terms in the second order average Hamiltonian, among which many are decoupled in the basic R6 and R8 sequences. In other words, the R4-based sequences benefit from super phase cycling most, and R4ixy3 and R4ixy4 show the most broadband ZQ polarization transfer under our simulation conditions, where decent polarization transfer can be achieved through broadband13C frequency range up to +/−40 kHz on a 600 MHz NMR spectrometer.

All the R4, R6 and R8-based sequences with ixy3 or ixy4 phase cycling could achieve high and uniform polarization transfer efficiency within a certain frequency range, which is highly advantageous for accurate determination of internuclear distances. Under MAS frequency of 40 kHz, the bandwidth where the transfer is uniform is ～ +16 to −16 kHz for R4ixy3,～ +12 to −12 kHz for R6ixy3, and ～ +10 to −10 kHz for R8ixy3sequences if the RF field strength is 60 kHz. Beyond these ranges, polarization transfer efficiency declines and fluctuates as the frequency difference varies. R4ixy3and R4ixy4sequences yield higher transfer efficiency than those with fewer steps in the phase cycle. On the other hand, not much improvement was observed for R6 and R8-based sequences when applying super phase cycles. For instance, in a narrow range of Δδiso, R6i and R6ixixcan achieve almost the same transfer efficiency as R6ixy4.When |Δδiso| > 40 kHz, R6 and R8 sequences with proper super phase cycles show slightly better transfer performance than R4ixy4, but all of these three kinds of RN sequences show nonuniform dependence of polarization transfer efficiency on Δδiso,which could be owing to the rotational resonance and the relatively low RF field strength.

The simulations for RN ZQ homonuclear recoupling at the MAS frequency of 20 kHz, as shown in Fig 2, reveal similar features to those performed for 40 kHz MAS. In addition, more clear patterns attributed to the rotational resonance conditions,i.e., |Δδiso| = 0, 20 and 40 kHz, are observed. The relatively low transfer efficiency could be partially related to the reduced scaling factors considering that the same RF field strength of 60 kHz was used at lower MAS frequency. With RN ZQ recoupling schemes, the scaling factors of (2, ±1, 2, 0) and (2, ±2, 2, 0)Hamiltonian terms are 0.134 and 0.076, respectively, for π pulses with RF field strength of 60 kHz at the MAS frequency of 40 kHz.These two factors decrease to 0.071 and 0.047 for the same RF field strength at 20 kHz MAS. In addition, the13C–1H dipolar interactions, which could not be effectively removed at low MAS frequencies, would interfere with the13C–13C ZQ homonuclear polarization transfer.

Fig. 3 Simulated dependence of homonuclear polarization transfer efficiency on RF field strength and the frequency difference between spin pairs at the MAS frequency of 40 kHz, for the following sequences: (a)–(c) basic R4, R6 and R8; (d)–(f) R4i, R6i and R8i;(g)–(i) R4ixy3, R6ixy3, and R8ixy3; (j)–(l) R4ixy4, R6ixy4 and R8ixy4. The mixing time was 2.4 ms. Labels A and B shown in (g) correspond to regions with relatively low transfer efficiency. 66 REPULSION angles (α, β) and 12 γ were used to get the powder average.

Fig. 4 Transfer efficiency plots of R4-based (a) and R6-based (b) symmetry sequences for ZQ homonuclear recoupling as a function of Δδiso, corresponding to the traces extracted from Fig. 3g and Fig. 3h, respectively. Black, red, green, blue and purple lines correspond to the RF field strengths of 20, 60, 80, 100 and 200 kHz, respectively.

Homonuclear polarization transfer efficiency changes enormously with varying the window fraction and depends on the relative size of the RF field strength and Δδiso. Fig. 3 shows the simulated dependence of homonuclear polarization transfer efficiency on13C RF field strength and the isotropic chemical shift difference between spin pairs for RN, RNi, RNixy3 and RNixy4 recoupling sequences at the 40 kHz MAS frequency. The mixing time was 2.4 ms for all simulations. There is a trend, RNixy4≈RNixy3> RNi> RN, in broadband ZQ homonuclear dipolar recoupling sequences, which is consistent with the simulation results shown in Fig. 2. Moreover, R4-based sequences perform better than R6 and R8-based sequences except for the basic R4.

Generally, it is challenging to achieve a truly broadband uniform transfer with RN ZQ symmetry sequences, even with super phase cycling. For instance, there remain two regions exhibiting low polarization transfer efficiency in R4ixy3simulations, as shown in Fig. 3g. In region A, the RF field strength is too high and close to the case of infinitely short pulse.This phenomenon could be explained by similar cases in RFDR schemes, where the magnitude of the polarization transfer approaches zero when the spin pairs have the same chemical shift and the π pulse length is negligible22. From another perspective, there are subtle correlations between window fraction and scaling factor in RN-based recoupling sequences,where too large window fractions lead to smaller scaling factor for basic R4, R6 and R8 elements. For the infinitely short pulse cases, the scaling factors approach zero for all four ZQ DD terms recoupled. In the practical NMR experiments, prolonging the mixing time could improve polarization transfer in A region due to its smaller recoupling scaling factor. In region B where the frequency difference, Δδiso, is comparable or even larger than the RF field strength of applied π pulses, the spin polarization could not be reversed efficiently, which leads to the low recoupling efficiency.

The polarization transfer efficiency is relatively high in the remaining regions, but not uniformly broadband. Rotational resonance recoupling could influence ZQ polarization transfer when RR conditions, Δδiso= nωr, are matched, which results in different dependence patterns when MAS rate varies, as shown in Fig. 2. Considering comparable performance but more phase steps for R8-based sequences, we will focus on the R4 and R6-based sequences in the following discussion.

To intuitively demonstrate the effect of13C RF field strength on ZQ polarization transfer by RNixy3schemes, several slices with representative RF field strengths were extracted from Fig.3g and 3h, and the corresponding results are shown in Fig. 4. For windowless RNixy3schemes (ω1= 20 kHz), the R6ixy3scheme shows lightly better recoupling performance, but the effective recoupling bandwidth is less than +/− 20 kHz. Windowed RNixy3 schemes (ω1> 20 kHz) with higher RF field strengths could dramatically broaden the effective recoupling bandwidth, but excessively high RF fields result in reduced polarization transfer efficiencies, especially for the spin pairs with small Δδiso. We could obtain uniform effective transfer efficiency with Δδiso up to +/− 50 kHz when RNixy3 with a RF field strength of 100 kHz was applied. Considering that13C spectral bandwidth of 200 ppm corresponds to 75 kHz at a 1.5 GHz NMR spectrometer, the results shown here demonstrate that these sequences could cover the entire bandwidth for13C–13C recoupling in most cases, which would allow for the determination of both spatial proximities(correlations) and internuclear distances. Furthermore, the results reveal that the optimized performance for finite pulse RN schemes under the present conditions can be achieved when ixy3 or ixy4 phase cycling with appropriate RF field strength is applied, and the suggested RF field strength would be, 1.5*ωr<ω1< 3*ωr, but not the previously reported value, 1.5*ωr(τp =τr/3). In addition, it can be noted that the R4ixy3 scheme shows less fluctuation than R6ixy3, and also due to the few phase steps in the cycle than in the R4ixy4. Taken together, the results suggest that R4ixy3could be the most efficient ZQ homonuclear dipolar recoupling sequence among all the sequences discussed here.

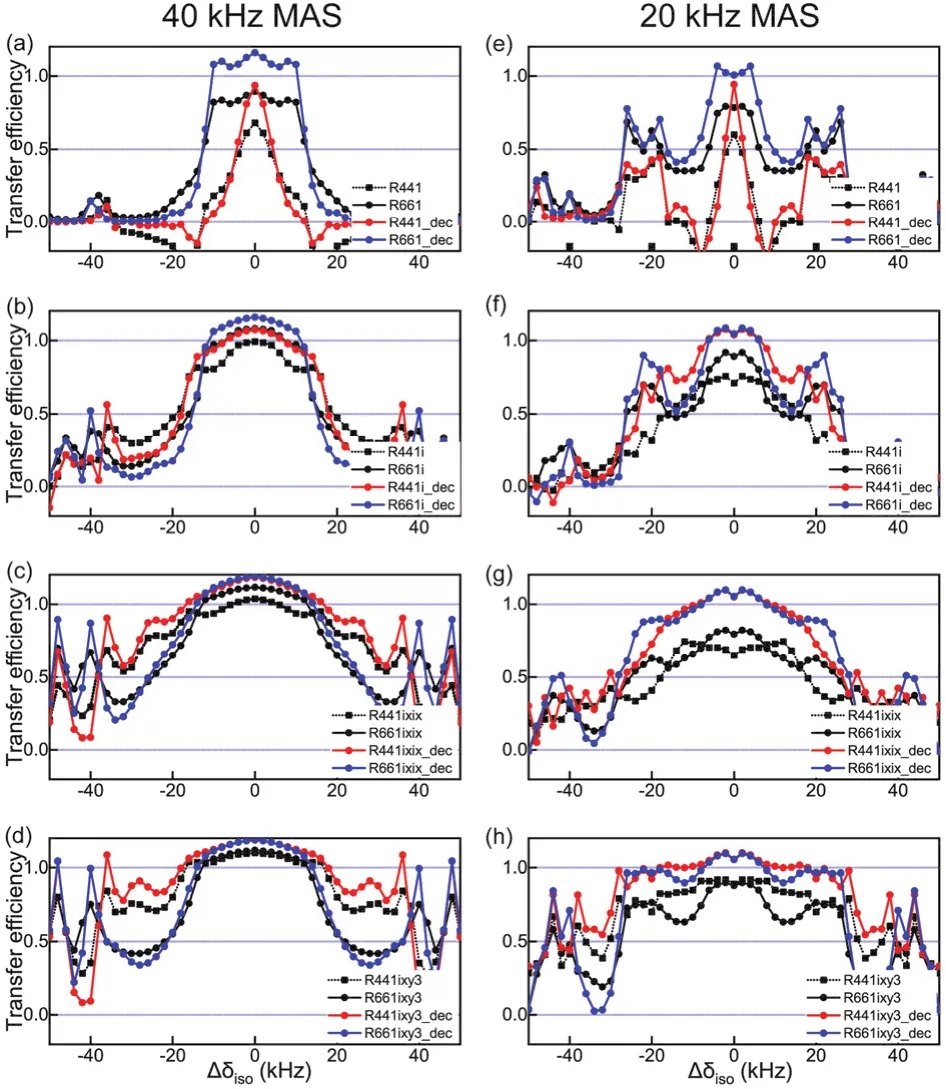
Fig. 5 Transfer efficiency plots for various R4 and R6-type symmetry sequences with or without 1H-decoupling as a function of frequency difference between spin pairs, Δδiso, at MAS frequencies of 40 kHz (a)–(d) and 20 kHz (e)–(h). High power proton decoupling with RF field strength of 250 kHz was applied during the mixing period wherever indicated; the other simulation parameters are same as in Fig. 2.

Under fast MAS conditions, low power1H decoupling irradiation might interfere with RN ZQ recoupling pulses, and no RF field or high power1H RF field decoupling may be more beneficial for efficient suppression of1H–13C dipolar couplings and for further enhancing the polarization transfer efficiency33.The influence of1H decoupling on RN ZQ recoupling efficiency was tested by simulations of C2H2spin system, as shown in Fig.5. At the MAS frequency of 40 kHz, high power1H decoupling could improve the RN ZQ polarization transfer, especially when Δδisois small. The band widths corresponding to efficient polarization transfer by RN schemes with1H decoupling are consistent with those without1H decoupling, and the R4ixy3scheme shows the broadest bandwidth. (We also tested R4ixy4that showed almost the same behavior as R4ixy3 under the MAS frequency of 40 kHz.) Considering that high power1H decoupling irradiation could lead to serious sample heating, RN ZQ homonuclear recoupling sans heteronuclear decoupling should be recommended at fast and ultra-fast MAS conditions33.

Simulations at the MAS frequency of 20 kHz were also executed to test the influence of proton decoupling at low-tomoderate MAS conditions, and the results are shown on the right side of Fig. 5. It is clear that1H decoupling makes RN ZQ recoupling work much more efficiently at low-to-moderate MAS conditions, which could be understood in light of the fact that low MAS frequencies cannot efficiently suppress13C–1H heteronuclear dipolar interactions, which in turn would interfere with RN ZQ recoupling. The results demonstrate that highpower1H decoupling is necessary during the RN ZQ recoupling period to improve the recoupling efficiency.

Fig. 6 Simulated dependencies of transfer efficiencies on RF mismatch and frequency difference between spin pairs at MAS frequency of 40 kHz, for R4-based schemes: (a) R4, (b) R4xy3, (c) R4i, (d) R4ixix, (e)R4ixy3, and (f) R4ixy4. The standard RF filed strength was 60 kHz, and was varied from 51 to 69 kHz, corresponding to RF mismatch up to±15%. The mixing time was 2.4ms. 66 REPULSION angles (α, β) and 12 γ were used to get the powder average.

Fig. 7 Simulated dependencies of transfer efficiencies on RF mismatch and frequency difference between spin pairs at MAS frequency of 40 kHz, for R6-based schemes: (a) R6, (b) R6xy3,(c) R6i, (d) R6ixix, (e) R6ixy3, and (f) R6ixy4. All other NMR simulation parameters are same as those in Fig. 6.

3.3 Sensitivity of various RN-based sequences to RF mismatch

RF field inhomogeneity is unavoidable in the overwhelming majority of commercial NMR probes, and pulse schemes with low sensitivity to RF mismatch would be more suited for practical applications. To assess the performance of RN ZQ recoupling schemes with various phase cycles, the sensitivity of R4- and R6-based symmetry sequences to RF mismatch was studied. Fig. 6 and 7 show the simulation results for R4 and R6-based sequences, respectively, with RF mismatch of up to ±15%(corresponding to RF field strength of (60 ± 9) kHz).

The results indicate that super phase cycling contributes to the reduced sensitivity to RF mismatch for both R4 and R6-based sequences, and RNixy3and RNixy4are preferential. R4-based sequences show better tolerance to RF mismatch than do R6-based sequences, and appear to be better across the board in terms of overall performance (see also discussions above).

Taken together, our results demonstrate that RN ZQ schemes with super phase cycles can efficiently achieve broadband homonuclear recoupling, and are also less sensitive to RF field inhomogeneity. Even though RNixy3sequence has fewer phase steps than RNixy4, it exhibits comparable recoupling efficiency and robustness.

3.4 Applications to a model compound and a microcrystalline protein

To further verify our findings from the simulations, various R4 and R6 sequences were tested on U-13C,15N-enriched Histidine and U-13C,15N-enriched microcrystalline LC8 samples. Representative examples of 2D13C–13C correlation spectra of histidine recorded at the MAS frequency of 40 kHz are shown in Fig. 8. It is clear that the spectra recorded with basic R6, R4ixy3or R4ixy4sequences contain more spatial correlations than that acquired with the basic R4 sequence. To have a clear insight into the difference among the various recoupling sequences, several 1D traces were extracted from the 2D spectra,to compare the signal intensities (polarization transfer efficiency) of the cross peaks. These are shown in Fig. 9 and Fig.10. The basic R4 recoupling sequence shows the lowest polarization transfer through the entire13C spectral range, which is consistent with simulations presented in Fig. 3. Among all RN ZQ recoupling sequences discussed here, the cross peak intensities are the strongest for the R4ixy3 and R4ixy4 schemes although the difference with respect to other sequences is not very pronounced. This result could be rationalized considering that the13C bandwidth of 200 ppm at the magnetic field of 14.1 T corresponds to 30 kHz, and under these conditions efficient polarization transfer can be easily achieved by most of the RN ZQ recoupling sequences discussed in the current work, in agreement with the results of the simulations. It should be noted that the intensities of diagonal peaks by R4ixy3or R4ixy4scheme are strongest as well, which suggests that the relaxation time(T1RF) introduced by R4ixy3or R4ixy4is longer than that by others.

As discussed above,1H decoupling could greatly enhance polarization transfer efficiency at relatively low MAS frequencies. To verify the influence of1H decoupling irradiation during the RN recoupling period, a series of 2D13C–13C correlation NMR experiments with or without high-power CW1H decoupling during the ZQ recoupling period have been performed on histidine at the MAS frequency of 25 kHz. The RF field strength for proton CW decoupling was 119 kHz (where used). Selected traces corresponding to different carbon species in the indirect dimension were extracted, and plotted in Fig. 11.The results demonstrate that1H decoupling could enormously improve ZQ polarization transfer, especially at low or moderate MAS frequencies, in accord with the simulations.

Fig. 8 2D 13C–13C correlation NMR spectra of U-13C, 15N-enriched histidine recorded at the MAS frequency of 40 kHz by (a) R4, (b) R6,(c) R4ixy3 and (d) R4ixy4 recoupling sequences with the mixing time of 2.4 ms. 1D traces for representative carbon atoms are labeled.The first contour in all spectra is set at 4 × σ (σ is the noise rmsd (root-mean-square deviation)).

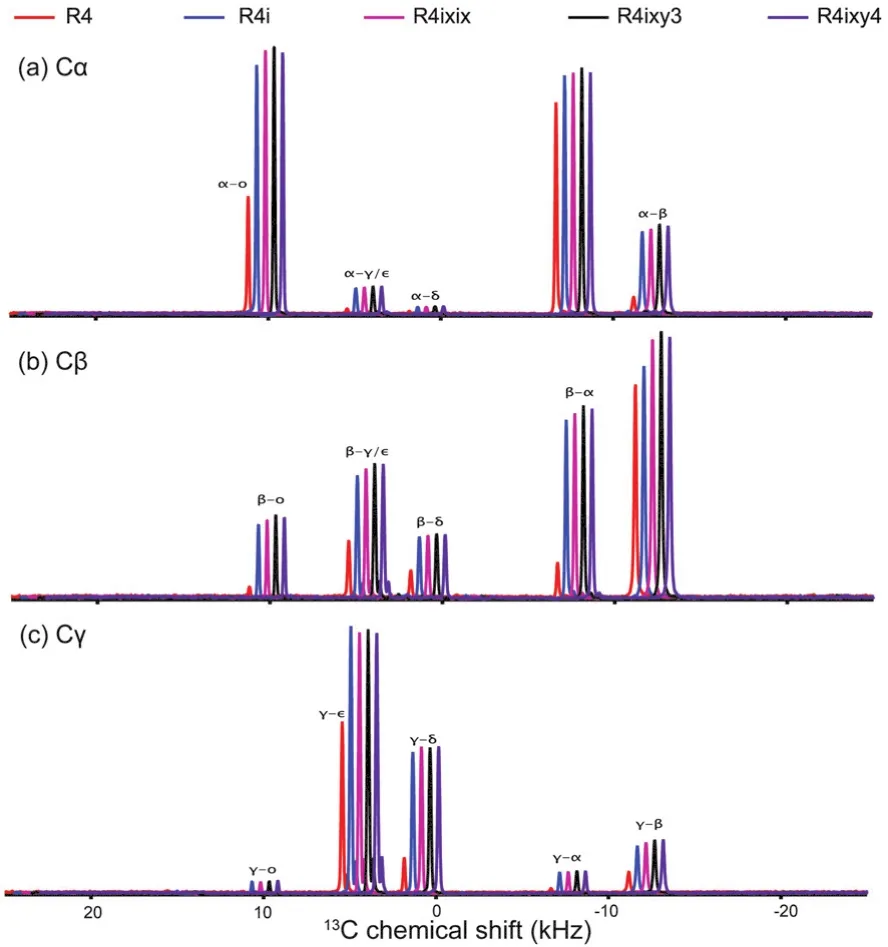
Fig. 9 1D traces extracted from R4-based 2D 13C–13C correlation NMR spectra recorded in U-13C, 15N-enriched histidine at the MAS frequency of 40 kHz, corresponding to (a) Cα, (b) Cβ and (c) Cγ in ω1 dimension. The mixing time was 2.4 ms.

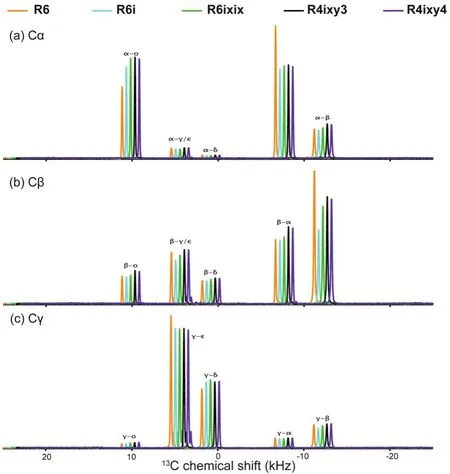
Fig. 10 1D traces extracted from R6 -based 2D 13C–13C correlation NMR spectra of U-13C, 15N-enriched histidine at the MAS frequency of 40 kHz, corresponding to (a) Cα, (b) Cβ and (c) Cγ in ω1 dimension. The mixing time was 2.4 ms. Slices extracted from R4ixy3 and R4ixy4 are also included for comparison.

Fig. 11 1D traces extracted from R4 and R6-based 2D 13C–13C correlation NMR spectra of U-13C, 15N-enriched histidine with or without high-power CW 1H decoupling at the MAS frequency of 25 kHz, corresponding to (a) Cα, (b) Cβ and (c) Cγ in ω1 dimension.The mixing time was 3.84 ms.

Fig. 12 13C–13C correlation spectra of microcrystalline U-13C,15N-enriched LC8 recorded at the MAS frequency of 40 kHz using(a) R4, (b) R6, (c) R4i, (d) R6i and (e) R4ixy3 recoupling sequences.The mixing time was 2.4 ms. The first contour in all spectra is set at 4 × σ (σ is the noise rmsd).

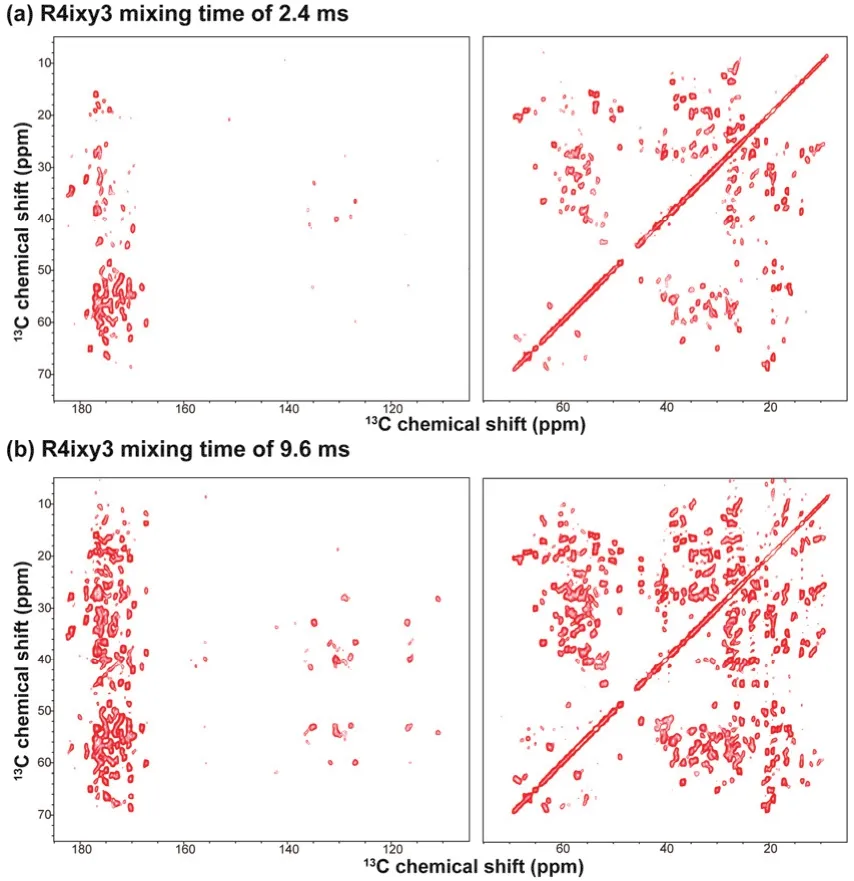
Fig. 13 13C-13C correlation spectra recorded on LC8 protein at 40 kHz MAS rate for R4ixy3 recoupling sequences with (a) 2.4 ms and(b) 9.6 ms mixing time. The first contour in all spectra is set at 4 × σ (σ is the noise rmsd).

To further verify the performance of RN ZQ recoupling schemes on systems of practical interest, we have applied R4 and R6 sequences with various phase cycles to microcrystalline U-13C,15N-LC8.13C–13C correlation NMR spectra were recorded at the MAS frequency of 40 kHz with a mixing time of 2.4 ms, and the results are shown in Fig. 12. Similar to the simulation results,the ZQ recoupling efficiency by basic R4 sequence is very sensitive to frequency differences and does not perform well for broadband recoupling. In contrast, the basic R6 sequence exhibits superior ZQ recoupling efficiency, and, interestingly, is comparable to that for R4 and R6 sequences with super phase cycles. In Fig. 13, the recoupling performance of R4ixy3sequence with mixing times of 2.4 ms (a) and 9.6 ms (b) is compared. As expected, many new cross peaks appear as the RN ZQ mixing time is increased, and these peaks might provide medium- to long-range spatial correlations in the protein sample. Although RN ZQ schemes suffer from the dipolar truncation, the enormous homonuclear and heteronulcear network would allow for the observation of multi-bond spatial correlations.

4 Conclusions

In this work, a series of RNN1-based (N ≥ 4, N is even)symmetry sequences for zero-quantum homonuclear recoupling have been studied theoretically and experimentally. Our results show that the basic R441sequence suffers from the influence of chemical shift difference and pulse imperfections, and is not an optimal ZQ recoupling scheme for broadband homonuclear correlation spectroscopy. However, the basic R6 sequence could efficient ly achieve ZQ dipolar recoupling within moderate bandwidth, which could be partly due to fewer second order cross terms in the average Hamiltonian. Nevertheless, the basic R661sequence still suffers from sensitivity to RF mismatch.Under low to moderate MAS conditions, high power1H decoupling could greatly enhance the polarization transfer efficiency, while homonuclear recoupling sans heteronuclear decoupling is recommended under fast MAS conditions.

Not only does super phase cycling enhance ZQ polarization transfer efficiency and bandwidth, but it also results in greatly reduced sensitivity to RF mismatch. In this regard, RNixy3and RNixy4sequences with 6*N and 8*N phase cycling steps,respectively, are preferred. Though R4ixy4(fpRFDR(XY8)41)sequence is robust with respect to RF mismatch, the R4ixy3 scheme introduced here could achieve comparable, or even slightly better, performance with fewer phase cycling steps. By choosing proper RF field strengths, 1.5*ωr< ω1< 3*ωr, uniform broadband ZQ recoupling with R4ixy3or R4ixy4sequences could be achieved under fast MAS conditions as shown in simulations,which would be significant for the accurate determination of spatial proximities and internuclear distances. Also, by tuning the mixing time, RN ZQ scheme could provide more cross peaks,where medium- to long-range spatial correlations could be included and are essential for structural determination in complex systems.