一类椭圆内接三角形的几个定值命题
广州市铁一中学(510600) 何重飞
广州市广东仲元中学(510000) ,严运华
熟知,若ΔABC是椭圆的一个内接三角形,且原点O是ΔABC的重心,则ΔABC的面积为定值笔者研究发现,以椭圆中心为重心的椭圆内接三角形有许多优美的性质,下面就这一类三角形的几个定值命题与大家一起探讨.
命题1椭圆上任意一点到以椭圆中心原点O为重心的椭圆内接三角形的三个顶点的距离的平方和与该点到椭圆两焦点距离的乘积的3 倍之和为定值
证明命题1,要利用如下两个引理.
引理1若ΔABC是椭圆=1(a >b >0)的一个内接三角形,且原点O是ΔABC的重心,则A,B,C三点的离心角分别为θ,θ+
证明依题意设A(acosθ1,bsⅰnθ1),B(acosθ2,bsⅰnθ2),C(acosθ3,bsⅰnθ3),则有
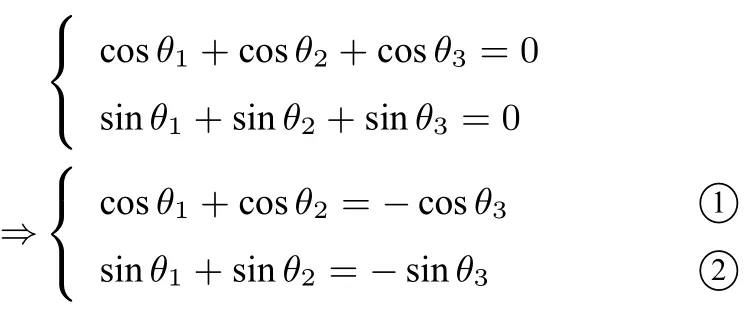
由 ①2+ ②2得cos(θ1-θ2)=同理可得cos(θ2-θ3)=故可设θ1=θ,θ2=θ+,θ3=引理得证.
引理2若ΔABC是椭圆=1(a >b >0)的一个内接三角形,且原点O是ΔABC的重心,则AB2+BC2+CA2=
证明由引理 1 可设 ΔABC的三点坐标为A(acosθ,bsⅰnθ),则有

同理BC2=3a2sⅰn2θ+3b2cos2θ,CA2=又因为

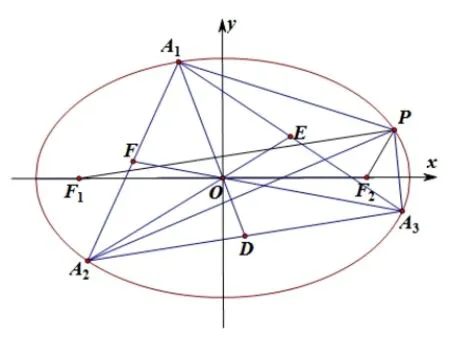
图1
命题 1 的证明如图1,设ΔA1A2A3是椭圆的一个内接三角形,且原点O是 ΔA1A2A3的重 心,ΔA1A2A3三条边A2A3,A3A1,A1A2长度分别为a1,a2,a3,点P是椭圆C上的任意一点,D,E,F分别是边A2A3,A3A1,A1A2的中点,F1,F2分别是椭圆C的左右焦点,记三条中线A1D,A2E,A3F的长度分别为m1,m2,m3,由中线长公式知


又因为
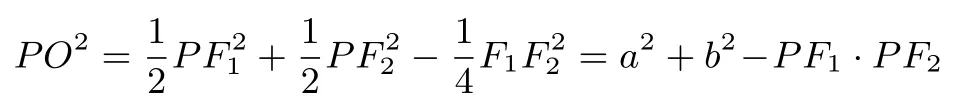


当动点P在Ai(i=1,2,3)时,即可得到
推论若ΔA1A2A3是椭圆C:的一个内接三角形,且原点O是ΔA1A2A3的重心,F1,F2分别是是椭圆C的左右焦点,则有
证明当点P在A1上时,由命题1 知3A1F1·A1F2=同理,当点P在A2和A3上时,
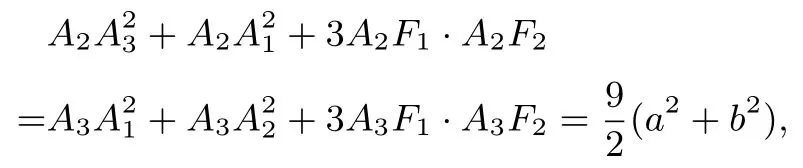
由命题1 及其证明过程亦可得到如下两个命题.
命题2若ΔA1A2A3是椭圆0)的一个内接三角形,且原点O是ΔA1A2A3的重心,点P是椭圆C上任意一点,F1,F2分别是是椭圆C的左右焦点,则有

证明如图1,由极化恒等式知

同理由命题1 及其证明知

又因为

所以有

命题3若ΔA1A2A3是椭圆b >0)的一个内接三角形,且原点O是ΔA1A2A3的重心,F1,F2分别是椭圆C的左右焦点,则有
证明由极化恒等式知

命题4若ΔA1A2A3是椭圆0)的一个内接三角形,且原点O是ΔA1A2A3的重心,若直线A2A3,A3A1,A1A2都存在斜率,且斜率分别为k1,k2,k3,则有

证明由引理1 可设A1(acosθ,bsⅰnθ),A2(acos(θ+则
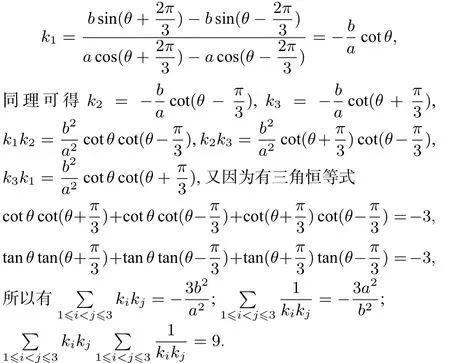
以椭圆中心为重心的椭圆内接三角形是否还有其他定值性质,或者其他圆锥曲线中是否有类似的定值性质留给感兴趣的读者进一步探究.

