运用柯西不等式巧解近年高校自招题

上海市行知中学(201999) 范广哲 胡昊劼

柯西不等式是数学中最重要的不等式之一，其应用特别广泛，在大学数学中经常起到非常关键的作用，如数学分析、线性代数、概率论、向量代数等分支中;在高中数学中同样有着非常广泛的应用，如不等式证明、函数求最值、解方程组等.柯西不等式的应用对培养中学生的数学抽象、数学运算、逻辑推理等数学核心素养有着非常重要的作用，同时也将有助于提高学生们发现问题、分析问题，进而解决问题的能力.

柯西不等式在高校自招数学题中也是频频出现，每次出现都能起到不同凡响的效果.本文列举的高校自招题都可以用柯西不等式的方法解决，阐述柯西不等式的奇思妙用，仅供读者参考和借鉴.部分题目来源于文献[1]，另外部分题目来源网络.其中部分题目也有很多其它方法，读者可自行思考.

首先，给出柯西不等式的表达形式，如下:

柯西(Cauchy) 不等式若a1,a2,··· ,an ∈R;b1,b2,··· ,bn ∈R，则

当且仅当bi=λai(其中λ ∈R,i=1,2,··· ,n)时等号成立.

特别地，若a1,a2,··· ,an;b1,b2,··· ,bn是两组非零实数，取等条件即为

柯西不等式的几个重要推论:

1.特别地，当bi=1(i=1,2,··· ,n) 时，柯西不等式为:进一步地，若ai ∈R+(i=1,2,··· ,n)，则

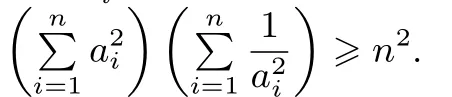
3.当ai,bi ∈R+(i=1,2,··· ,n)时，则

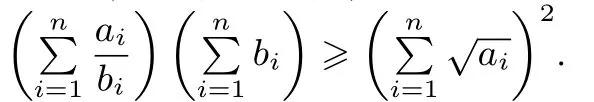
柯西不等式有很多种证明方法，本文不再赘述.柯西不等式的上述几个推论在本文也有所体现，这些结论对于解题来说非常重要，能够带给解题人意想不到的联想与收获.在平时的学习过程中，要重视及时归纳总结.二元与三元柯西不等式一直是高校自主招生中考查的热点，本文列举几例近年高校自招题以此体现柯西不等式的妙用.

类型一: 二元柯西不等式

二元柯西不等式的应用范围非常广泛，本节的举例主要是与求函数最值相关，要注重构造柯西不等式的形式.另外等号成立的条件也需要验证.

例1(2019年北大暑期学堂测验) 实数x,y,z满足x+y+z=x2+y2+z2=2，求xyz的最大值和最小值.

分析题目条件为两个方程，首先考虑消元法，把所求表达式化成知含有一个未知量的形式，最后归结求解函数最值问题.但本题特别要注意未知量取值范围，考虑利用柯西不等式求解.

解析由题可得，x+y=2-z，x2+y2=2-z2.由柯西不等式得，(2-z2)(1+1)≥(2-z)2，解得由于因而f(z)=xyz=z(z-1)2=z3-2z2+z.由f′(z)=0 可得，或z=1.因而，f(z)mⅰn=f(0)=f(1)=0，

例2(2017年北大暑期学堂测验) 求函数f(x)=的最大值.

分析本题是一道求函数最值问题，观察其形式具有根号，首要考虑其定义域，由于两根号里面之和是定值，由此可拼凑成二元柯西不等式的形式.本题亦可使用均值不等式方法.

解析由柯西不等式可得:

50=[(x-6)+(31-x)](1+1)≥当且仅当时等号成立.解得符合6 ≤x≤31.可得，因而

例3(2013年中科大自招) 求函数f(x)=的最大值.

分析本题是一道求函数最值问题，观察其形式含有x和x2的项，由此可拼凑成二元柯西不等式的形式.

解析由柯西不等式可得:

类型二: 三元柯西不等式

三元柯西不等式的应用极为广泛，特别是在三元不等式求解最值问题时.本节列举几例来说明三元柯西不等式在解题中的运用.若条件和求证表达式具有对称性，这时可先尝试考虑当题目中所有元相等时，并求出其值，验证结论的等号是否成立，若成立，则在运用不等式方法求解过程具有一定的启发作用.

例4(2018年清华大学自招试题)已知x≥0,y≥0,z≥0，且满足4x2+4y2+z2+2z=3，求5x+4y+3z的最大值.

注本题原题是一道求解最大值与最小值的问题，本文只考虑最大值的情况.

分析本题是一道非常典型的三元最值问题，条件形式要注意把含z的项构造成平方形式，再运用三元柯西不等式求解.

解析由柯西不等式可得，

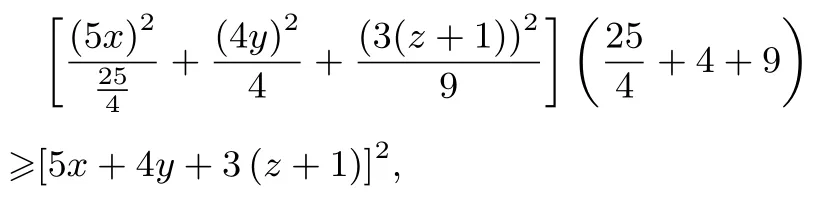
例5(2016年中国科学技术大学自招试题)已知a,b,c ∈R+，a+b+c=3，证明:

分析本题所需证明的表达式具有一定的对称性.问题关键是如何构造变形表达式使其与题目条件建立适当的联系，进而达到放缩的目的.

证明由柯西不等式得，

由二元均值不等式，a+b≥当且仅当a=b=c时等号同时成立.进一步可得，3=a+b+c≥因而

例6(2013年北京大学金秋营试题)已知x,y,z ∈R+，且满足x+y+z=3，证明:

分析本题具有一定的难度，但由于其结论形式具有轮换对称性，可以考虑分离求解.如何把结论的表达形式变形使其与条件建立联系是本题的难点，这就需要解题时进行适当拼凑尝试，当一次变形无法到预期效果，尝试进行多次使用不等式，但要验证两次等号时的条件是否一致.

证明由柯西不等式可得，

由于xy+yz+zx≤=3，当且仅当x=y=z=1 时等号成立.代入可得

例7(2013年中国科学技术大学自招试题) 已知α,β,γ ∈且满足cos2α+cos2β+cos2γ=1，证明: tanαtanβtanγ≥

分析本题是一道三角不等式的证明题.考虑分析法，首先从结论出发，切化弦，再把正弦化余弦，整理发现后其形式和条件可以构造三元柯西不等式的形式，然后再把思考的过程逆向写出即为解题过程.当然也可以考虑换元，进而把表达形式变得更为简单.

证明由柯西不等式可得，

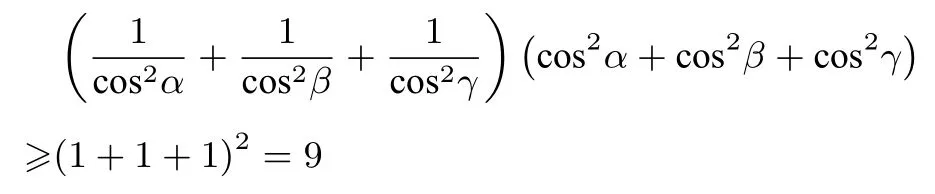
(1-cos2α)(1-cos2β)(1-cos2γ)≥8cos2αcos2βcos2γ,即sⅰn2αsⅰn2βsⅰn2γ≥8cos2αcos2βcos2γ,因而，(tanαtanβtanγ)2≥8.由于α,β,γ ∈因而tanαtanβtanγ ＞0，可得tanαtanβtanγ≥