非等间距GM(1,1)幂指数优化模型在变形监测中的应用
魏家猛,刁建鹏 ,姜华根
(西南林业大学 土木工程学院, 昆明 650051)
随着现代化发展进程的脚步,中国基础建筑飞速发展,机场、高铁、地铁等与日俱增,施工期间,随着进度的发展,建筑物必定会随着荷载的增加发生沉降现象,为保证工作顺利进行,必须对建筑物进行变形监测,借助仪器对动态的建筑物进行静态的、周期性的测量,将获得的数据进行基准网稳定性分析以确保监测数据的可靠性[1]。将每期获得的数据进行整合,并以时间序列为因变量寻找观测值与时间序列之间存在的不确定性关系,用熟知的模型将这种不确定性关系表达出来,再对建筑物进行预测。常见的模型有小波神经网络、灰色模型、回归分析和时间序列等。
20世纪80年代中国学者邓聚龙教授创立了一门以“小样本,贫信息”不确定性系统为研究对象的新理论。因其独特的优点广泛应用于不同的领域,并取得优异的成果[2]。如刘思峰、党耀国等通过分析误差出现的原因,确定了背景值对灰色模型预测范围的影响[3]。花向红、 李海英等将灰色模型和神经网络进行组合,并成功应用于变形监测[4]。黄声享、李志成等将非等间距模型进行变换处理解决了沉降观测中灰色模型必须等距的的实用性问题[5]。这些学者的研究使灰色模型得到了充分的发展。
本文在灰色非等间距模型幂指数模型的基础上利用灰色模型中差商近似代替微商,推导出求解非等间距幂模型中幂指数γ的计算公式。与常规回归分析建模进行对比,并验证了该方法适用于变形监测的有效性、正确性和实用性。
1 回归分析
1.1 非线性回归方程定义
在求非线性回归方程时一般可分为2步,第一,确定函数的类型,可以根据散点图中数据组成曲线的形状进行确认。第二,求解与函数相关的参数,在利用最小二乘求解非线性回归方程时是非常复杂的,通常情况下是通过变换自变量和因变量将回归曲线变换为常用的一元线性方程进行求解;或者将曲线进行多项式拟合,通过多项式将2个变量之间的关系描述出来,把曲线回归转换为常用的多项式回归,简化问题[6]。
将预选的回归曲线f(x,y,a,b)=0线性化写为:
v=A+B×u
式中的v,u是分别只含一个变量关于x和y的函数,A、B是关于参数a、b的函数。
利用最小二乘估计得出a、b的最优估值,此后用一元线性回归方程来描述非线性回归方程之间的关系,如下:
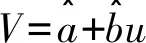
在得到一元线性回归方程后利用函数逆变换还原目标函数得到非线性回归方程。
1.2 回归方程的拟合精度评估
(1) 回归方程的稳定性
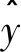
式中σa、σb为a、b的标准差;σab为a、b的协方差。
(2) 回归方程的方差分析
观测值之间的差异用观测值与其算术平均值的离差平方和表示,称为总离差平方和,如下
将总离差平方和进行分解,最终可以得到由回归平方和和残余平方和表示的总离差平方和,其表示如下:
也可简化为:
S=U+Q
U为回归平方和,反映了在y总的变差中由x和y的线性关系引起的y变化的部分,即在总离差平方和中占得比例,Q为残余平方和,反映观测值与预测值之间的差异,也可以解释为x和y之间线性关系以外的影响因素,Q越小拟合程度越好。
(3)R2检验
为验证回归方程中y和x之间的线性关系是否显著,作假设H0:β=0,即y和x之间不存在线性关系。由回归方程的方差分析可知U在S中所占的比例越大,x和y的线性关系越强烈,因此定义R2为衡量曲线拟合的指标[6],如下:
R2为相关系数,由上式可看出R的取值为(0,1),一般在范围0.8~1内,可以认为回归平方和所占的比例大,拟合程度好,自变量与因变量具有很强的相关性。
(4) 显著性检验
在假设H0:β=0下,即y和x之间不存在线性关系。构造统计量F:
式中f为自由度,
如果在显著水平α下,F>F(f,n-f-1),则认为回归方程式显著的,方程系数不显著为零,可以进行预测。
2 非等间距幂模型参数优化模型
2.1 非等间距幂指数优化模型定义
设原始非负序列为x(0)(t)={x(0)(t1),
x(0)(t2),…,x(0)(tn)},其中,△tk=tk-t(k-1)≠const,k=2,3,…,n,对原始序列进行累加生成:
{x(1)(tk)={x(1)(t1),x(1)(t2),…,x(1)(tn)}
式中

将序列x(1)进行紧邻均值生成得序列:Z(1)=(Z(1)(t2),Z(1)(t3),…,Z(1)(tn))
其中,Z(1)tk=0.5(x(1)tk+x(1)t(k-1)),k=2,3,…,n
则非等间距GM(1,1)幂模型的灰色微分方程模型为:
x(0)+aZ(1)(tk)=b(Z(1)(tk))γ
特别,当γ=0时上式为非等间距模型,当γ=2时为灰色非等间距Verhulst模型。因此,处理好γ的选择问题就能建立精确的预测模型[7]。
2.2 参数求解
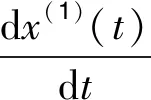
+ax(1)(t)=b(x(1)(t))γ的两边同时除以
(x(1)(t))γ得:
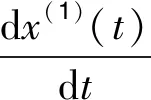
对上式中的t进行求导并整理可得:

[x(0)(tk)]2×[Z(1)(tk)]γ-1=a×(γ-1)×
[Z(1)(tk)]γx(0)(tk).
同理,当t=tk+1时可得:

将上式进行相除消去参数a,整理上式后可得幂指数γ的计算公式:

取k=2,3,…,n-1时,可以得到n-2个γ值,记为γk,构造关于γ的函数g(γ)如下:
令
由函数可以看出,在函数取最小值时的γ就是所求的最优估值。根据极值存在条件可得:
将上述得到的估值γ带入模型的微分方程,通过求解,最终得到参数的表达式如下:

由此非等间距幂指数模型的响应时间式为:
还原式为:
2.3 预测模型检验
灰色非等间距幂模型是否能应用于变形监测,其可靠性与精度检验可以由残差大小检验,关联度检验,后验方差检验等进行判断,采用残差统计特征进行后验方差检验,以预测值或拟合值残差为基础,求取检验后方差比c和小误差概率值P,以后验方差和小概率的值大小评判精度[8],参照标准如表1。步骤如下:
(1)求取残差:
(2)残差均值及测量值均值。
(3)残差的方差值:
(4)原始数据方差:



表1 精度等级表
3 实例分析
某建筑在施工过程中,为确工程安全,进行沉降观测。选取8期数据进行分析,其中前7期为建模,第8期作为预测。在回归分析中,由于数据为负序列,无法进行对数变换。因此,利用数据的变换将原始数据变化量进行Y=Y+10变换,方便多种回归模型的的选择和建立,最终进将得到的预测数据进行还原,得到需要的预测数据。以下数据皆是在Matlab中进行编程计算的,表2为数据整理的结果。
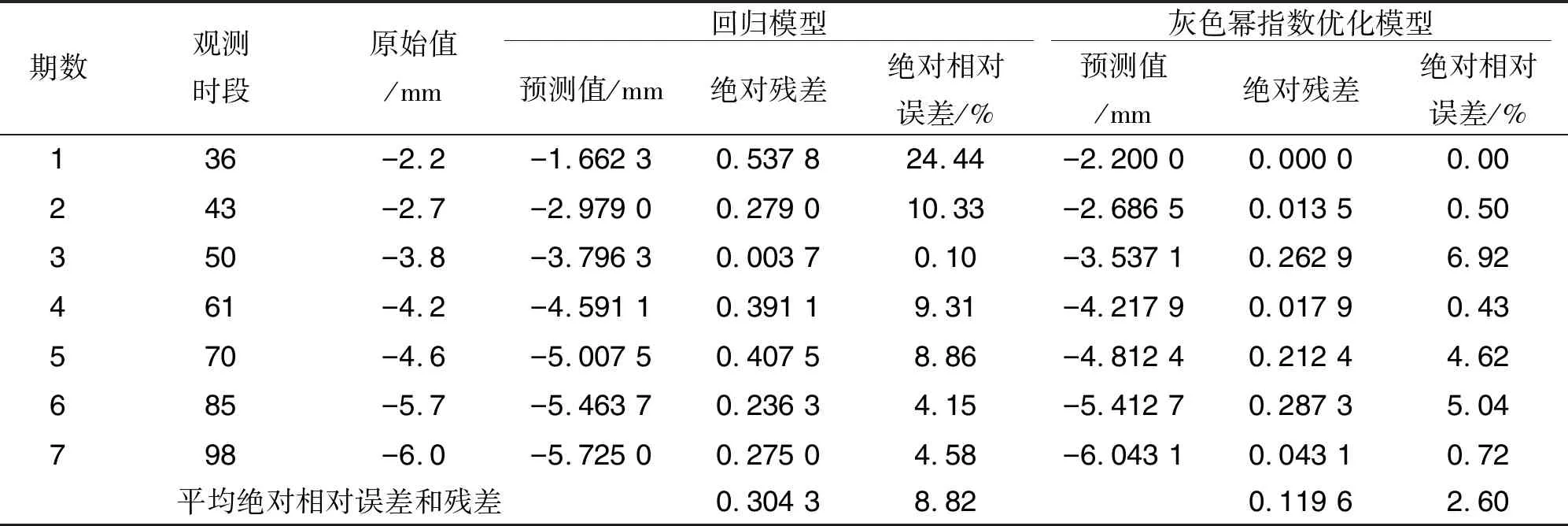
表2 预测成果表
3.1 精度分析
在上表中,回归方程的拟合效果指标R2为0.935,说明拟合度很不错,显著性检验统计量F为72.168,可认为回归是高度显著的。在非等间距幂指数模型的预测中,后验差c为0.0155(≤0.35),小概率P为1(≥0.95),根据灰色模型精度评定标准为1级。2者皆满足建模的精度需求,因此可以进行数据的预测。将第8期数据进行预测检验拟合效果,如表3模型预测表。

表3 模型预测表
3.2 模型分析
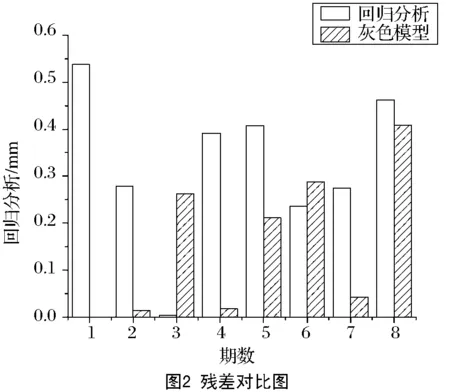
表3对2种模型进行了预测检验,回归分析的预测数据为-5.7374,残差为0.4626,灰色模型预测值为-6.6093,残差为0.4093。通过2种方法的进行的预测值对比,回归分析绝对平均残差和相对平均误差分别为0.3043和8.82%,灰色模型的绝对平均残差和相对平均误差分别为为0.1196和2.6%,由拟合效果图图1可以看出2种方法都可以很好地拟合出变化曲线,在图2残差对比图中可知2种方法的预测效果皆在毫米级以内,且灰色模型的残差普遍小于回归分析,灰色幂指数优化模型拟合效果较优于回归分析。

4 结论与建议
通过灰色模型与回归模型的数据对比分析,灰色幂指数优化模型可以应用于建筑物的沉降预测,并能在一定程度上提高模型的预测精度。故此, 灰色幂指数优化模型可以作为一种建筑物沉降预测的预测手段。
由于幂指数模型对原始数据较常规模型更为灵敏,在数据获取过程中应当确定数据的准确性。尽量减少粗差和观测方法对原始序列造成的影响,保证预测模型的拟合精度。

