构建知识网络 促成有效复习
—— “函数与方程、不等式”复习课的设计与思考
尹 嵘 吴 敏
(北京市铁路第二中学,100045)
数学复习课怎么上?怎样设计并实施有效的教学活动,促进学生夯实“四基”,培养数学核心素养?本文以“函数与方程、不等式”复习课的设计为例,力图通过“问题串”促进学生学会思考,感悟函数思想在研究方程与不等式中的作用,初步构建知识网络.
一、学情分析
从学生学习习惯上看,他们通过摸索和磨合,正在逐步适应高中数学课堂的“容量、节奏、难度和方式”,并找到(或正在寻找)一个最适合自身的学习习惯和方法.
从知识技能上来看,学生经过前面函数内容的学习,经历了从初中到高中的“定义的升级、表示形式的抽象化和多样化、函数性质的丰富、基本初等函数类型的增加”等等,是一个不小的考验.通过对三种具体函数:幂函数、指数、对数函数的研究,对函数的概念和性质有了进一步的直观的理解和认识,也初步掌握了研究函数的一般方法;而“函数的零点”的学习,也使得学生对“函数与方程、不等式”的关系有了新的认识,初步领会到“函数思想”对“解方程、不等式”的研究意义.
本节课除了在知识上的回顾复习,注重将学过的知识串起来,逐步构建知识网络,并让学生在学习中通过“数形结合”,培养类比和归纳能力,体会数学思想,夯实“四基”.
二、教学目标
(一) 知识与技能
1.理解函数零点探求的不同方法,初步掌握利用函数性质来分析零点;
2.进一步理解函数零点存在性定理的适用条件,以及定理是函数存在零点的充分不必要条件;
3.理解均值不等式的函数背景,初步掌握构建函数,利用函数性质研究不等式
(二)过程与方法
从熟悉“一元二次方程的根的分布”的背景入手,让学生通过实践,经历“从数到形”的体验过程,并进行初步的归纳推理和结论推广.在此基础上,根据函数的性质,对“函数的零点问题、不等式的恒成立问题”进行“数形结合”的深入思考和尝试,体会“函数与方程思想”,培养学生的逻辑推理和直观想象的核心素养.
(三)情感态度与价值观
通过探究实践,特别是通过直观观察、逻辑推理,帮助学生积累数学活动经验,体会其中蕴含的数学思想,感悟并培养数学表达和解决问题的能力.
三、教学重点与难点
重点:理解“函数与方程思想”,初步掌握函数思想在解方程和不等式恒成立中的应用.
难点:函数与方程、不等式的联系,选择适当的方法来解方程和不等式恒成立问题,体会函数思想解决“方程与不等式”中的作用.
四、教学过程
(一)复习回顾
1.一元二次函数、指数函数和对数函数图象的基本作图法及注意要点;
2.零点存在定理及适用条件;
3.平均值不等式求最值的适用条件.
(二)问题探究和实践
1.在一元二次方程的实根分布中的运用
例1关于x的一元二次方程x2-ax+3-a=0,求当a为何值时,分别有以下的结论:
(1)方程有两个正根;
(2)一根大于2,一根小于2.
分析从用韦达定理和用函数图象特征两个不同的角度来分别探究.
思考1对于一元二次方程根的分布有几个常见的解决方法?
(1)方程角度,其关键是根的判别式及韦达定理;
(2)函数角度,主要依据是函数图象,对称轴、最高点与最低点;
(3)零点角度,主要是零点存在定理
归纳从韦达定理和函数图象两个角度,对于一元二次方程ax2+bx+c=0,(a>0)有两个正根、两个负根、一正一负两个根等常见类型进行归纳总结.
设计意图从学生的最近发展区入手,学生能够上手,并自主探究“数形结合”的多种方法,打开探索的思路,并归纳一般的方法,初步体会利用“函数图象”特征对方程的根的分布的影响.
2.函数的零点问题
例2(1)函数f(x)=x+lnx-3的零点所在的区间为( )
(A)(0,1) (B)(1,2)
(C)(2,3) (D)(3,4)
解析方法1:利用零点存在性定理;
方法2:用数形结合,转化为g(x)=lnx,h(x)=-x+3的图象的交点横坐标所在范围.
分析方法1:用直接解方程的方法;
方法2:用函数图象平移的方法来分析.
思考2关于零点问题,若对应的方程的根易求时,可以直接解方程求根,注意要满足定义域即可;如果用函数图象求解,要关注函数的性质(单调性、奇偶性等等)、函数图象的渐近线、函数图象的端点的实虚等等,并结合零点存在性定理.
设计意图在初中所学基本初等函数的基础上,结合高中学习的幂函数、指数函数和对数函数,形成更加丰富的函数载体范围.在此背景下进行函数零点的探求,让学生进一步熟悉基本初等函数的图象和性质,并通过“数形结合”探究函数零点分布的不同方法,构建知识网络.
例3设函数f(x)是定义在R上的奇函数,当x>0时,f(x)=lnx+x-1,则f(x)的零点为______.
分析通过观察法,借助函数性质,可得共有3个零点:-1,0,1.
设计意图让学生明确,看出来的零点只能说明存在性,是否具备唯一性(就是还有没有别的零点),还需要借助函数的性质(单调性、奇偶性等)来研究.
思考3函数零点个数的探求方法
① 解方程:当对应的方程易解时,可通过解方程,看方程是否有根落在给定的区间上;
② 零点存在性定理:要求函数在[a,b]上是连续不断的曲线,且f(a)·f(b)<0,还必须结合函数的图象与性质(单调性、奇偶性),才能判断函数有几个零点;
③ 利用图象交点的个数:画出两个函数的图象,看其交点的个数,其中交点的横坐标有几个不同的值,就有几个不同的零点.
例4能说明“若定义在R上的函数f(x)满足f(0)f(2)>0,则f(x)在区间(0,2)上不存在零点”为假命题的一个函数是______.
分析联想二次函数的图象构造反例:f(x)=(x-1)2.
思考4函数f(x)在[a,b]上是连续不断的曲线.且f(a)·f(b)<0,则在(a,b)上f(x)存在零点.如果要判断函数有几个零点,则必须结合其图象与性质(单调性、奇偶性).
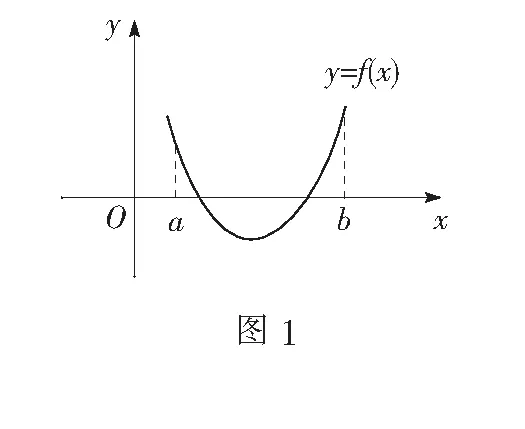
注意函数f(x)在[a,b]上是连续不断的曲线,且f(a)·f(b)<0,满足这些条件一定有零点.但不满足这些条件也不能说一定没有零点.如图1,f(a)·f(b)>0,函数f(x)在(a,b)上照样存在零点,所以函数零点存在性定理是函数存在零点的充分条件,而不是必要条件.
设计意图从充要条件角度来理解函数零点存在性定理,加强逆向思维的培养,使得学生对定理理解更加深入.
3.函数与不等式
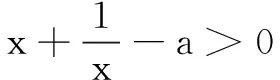
(2)若将x∈(0,+∞)改为x∈[2,+∞),则实数a的取值范围为______.
分析两问均可转化为函数的最值问题,即:a 注意:(1)用平均值不等式; (2)借助于(对勾函数)单调性求最值. 思考5在平均值不等式的等号条件不能满足时,常可以考虑用对应函数的单调性来研究. 设计意图函数与不等式的关系,学生在学习一元二次不等式的图象解法时已有初步了解.平均值不等式作为求函数最值的重要方法,学生要理解应用的条件,更要从函数角度来理解其本质,打通函数与方程、不等式之间的关系. 分析方法1:求函数最值的方法,即转化为:f(x)min≥a. 方法2:利用函数图象特征求解. 方法3:利用分离参数法求解. 思考6与二次函数有关的恒成立问题的求解,常用的方法: ① 借助函数图象的分布,转化为求函数在区间上的最值或值域问题. ② 借助于二次函数的图象特征来求解,注意考虑开口方向、对称轴、判别式、端点值等等; ③ 尝试分离参数法,回避分类讨论. 设计意图感悟二次函数与二次方程、二次不等式之间的联系,探究从不同的思考角度,来构建适当的函数,并利用函数的性质来解决不等式的问题.在学生的自主探究中,促使学生进一步构建“函数、方程与不等式”的知识网络,通过自主思考和与他人讨论,丰富活动经验,培养数学思想. 1.求函数y=f(x)的零点和解方程f(x)=0求根是一致的,但方法却是多样的,特别是要注意数形结合,利用函数的图象来帮助分析解题. 2.与函数知识结合的不等式解题时往往以不等式为工具,结合函数性质通过推理来解决问题 3.要有“函数与方程的思想”,即利用函数性质来解决问题的意识.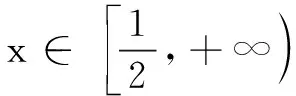
(三)课堂小结

