基于唤醒与生成的数学探究课堂

魏荣

摘要：培养学生做学习的有心人，甚至是知识的发现者，其手段是多样的，可能是顿悟之后的发现与证明，也可能是解决问题过程中的自然生成。后一种方式在课堂教学中表现为：基于学生的认知基础，利用并开发教材，创设自然的发散思维情境，唤醒旧知识，引导学生通过联想、试错、整合，在问题的解决过程中，逐步弱化条件，探索并获得新知识。

关键词：勾股定理;自然思维;探究课堂;教学逻辑;唤醒;生成

作为直角三角形的性质，勾股定理揭示了直角三角形的三边关系，是用来求解线段的长度的最重要手段;作为欧氏几何的基础定理，勾股定理的证明是论证几何的发端定理，是逻辑推理教学的契机;作为数学文化的重要组成部分，勾股定理的发现与发展史，是课堂教学活动不可或缺的。基于此，“勾股定理”第一课时教学定位为探究定理的获得及简单应用，渗透数学文化，体会数学知识的发现与生成过程。

一、问题的提出

如果忽视定理的发现与证明过程，以定理的应用为教学目标，显然不符合义务教育数学课程标准对培养学生“发现和提出问题、分析和解决问题能力”的要求。发现问题比解决问题更有价值，通过定理的发现过程，获得基本活动经验，培养学生的问题意识、创新意识。对于如何发现、探究勾股定理，在平时的教学中，我发现如下一些现象。

现象1：从毕达哥拉斯的发现（如图1）入手，引入网格验证特殊的直角三角形的三边与相同边长的正方形的面积关系，发现赵爽弦图，从而得到验证。

现象2：从制作类似于沙漏的教具（如图2）入手，发现三个正方形的面积关系，得到猜想，再通过拼图验证。

现象3：从特殊直角三角形入手，由等腰直角三角形三边关系引导计算，发现平方关系，从而联想正方形的面积，引入网格图，验证特殊的直角三角形，发现赵爽弦图，从而得到验证。

现象4：通过“画一画”“量一量”“算一算”等方式，让学生发现直角三角形的三边不是一次关系，进而猜想平方关系，引入正方形，再由割补法验证。

“观察、实验、猜想、验证”，是数学研究的重要手段。以上几种教学设计正是基于这个思路。但是，本节课用这种思路教学，学生如何发现命题的存在（特别是平方关系）？为什么会想到用面积法验证？这将是课堂教学面临的最大困难。

1.毕达哥拉斯的发现作为文化史，说明数学无处不在，可以鼓励学生要善于观察，发现生活中的数学。现象3仅从等腰直角三角形计算，特例太少，如何归纳？现象1、现象2、现象3故意为之的痕迹太明显，有告诉学生结果之嫌。

2.现象4试图通过一般化的计算发现问题，但是无理数如何测量？如何解释直角三角形的三边不是一次关系或其他关系？

3.在没有发现或给予平方关系的情况下，如何想到面积法？面积问题为什么会想到用网格辅助解决？没有引出网格，发现弦图，验证的难度可想而知。

二、教学设计

基于以上考虑，本节课将定理的发现与验证过程定位为：出于思维过程的合理性，由原有知识（实数

的获得）出发，利用思维惯性，发现拼图的价值，并逐步一般化，在面积法求解一般直角三角形的斜边长的过程中，因目标驱动，自然地发现并验证勾股定理。历史名家的发现过程与验证思路改为在数学文化渗透中简单体会。

流程：感受边的关系的存在（确定研究方向）→简单特殊情况探究（寻找研究手段）→从一般性情况获得定理（自然生成新知）→定理的简单应用（知识应用价值）→定理的文化史简介（他人发现过程）→前人对定理的证明（了解不同方法）→课堂小结学法及定理（回顾归结生长）

活动1：引导研究方向

【问题设计】

1.在三角形的研究中，我们采取了从一般到特殊的方法，有哪些特殊三角形呢？

2.说说学了等腰三角形的哪些内容？

3.直角三角形呢？如何研究？

4.如果a、b确定，c的值可以确定吗？说说你的理由。

【设计意图】问题1、2让学生体会几何学习的基本方向，也就是研究图形的定义、性质与判定，在性质研究中抓住边、角、特殊线段等，确定课题的研究内容。

问题3、4作为直角三角形三边关系发现的第一步：相对于一般三角形来说，条件强化，发现三边的确定关系。

【预设生成】问题4作为这个环节的难点，体现问题的确定性，学生可能存在解释困难，可提醒学生作图，联系全等三角形的知识，发现a、b确定的同时，c是唯一确定的。这个结论说明了c是可求的，从而找到本节课的重点——已知两直角边a、b，探究斜边c的求法。

活动2：定理的发现与验证

【问题设计】

1.从简单特殊入手

問题1：已知Rt△ABC，∠C=90°，若 a=b=1，你能求出c吗？

问题2：若 a=2， b=3，你还能求c吗？

2.如果一个直角三角形的两直角边是a、b，还能求斜边c吗？

3.在计算过程中，得到一个关于a、b、c的结论，即a2+b2=c2。由于a、b、c是直角三角形的三边，所以这个结果就是直角三角形的三边关系，我们把它称为勾股定理。

4.归纳：定理、几何语言

【设计意图】从简单特殊图形入手，给定具体的直角边，便于计算，符合研究的过程，更为了引出面积法原理。在处理问题1和问题2中体会差异，在差异中找到共性，理顺方法，达到一般化的目标，让定理的获得水到渠成。

特别是问题2，仍从具体的直角边长求面积，便于计算。完成两个目标：一是明确求大正方形的边长，目标是求大正方形的面积;二是在求中间小正方形的面积计算中，找到一般情形的处理办法。

【预设生成】问题1的解决方法是多样的，给足学生时间，从已有知识、学情出发，展开探讨，其结果对个别学生来说也可以作为定理的猜想起点。如果存在困难，可以作如下引导：

（1）你熟悉直角三角形的什么？

（2）回顾学习实数时，如何得到_________？

学生基于小学的学习经验，一般可以联想到面积，可能通过作斜边上的高或拼两块等腰直角三角形完成。通过以上几种解法，给学生简单说明面积法，明晰本节课推理、计算的依据。

问题2的设置是一般化的过程，可以培养学生的动手操作能力，在问题1的基础上经历探究试错的过程。在试错中识别图形特征，如拼成的四边形的四个角是不是直角;在试错中巩固原有几何知识，如等腰三角形的三线合一;在试错中找到弦图，明确知道两条直角边就可以求得斜边。

顺水推舟，把具体的数换成字母，通过整式运算、恒等变形，自然就得到勾股定理。

活动3：定理的简单应用

【问题设计】

1.（1）勾股定理有什么用呢？舉例说明;（2）变形等式。

2.练习：Rt△ABC中，∠C=90°，两条直角边为a、b，斜边为c。

（1）已知a=6，c=10，求b;（2）已知a=5，b=12，求c;（3）已知c=25，b=15，求a。

3.已知一个直角三角形的两边长分别为3和4，则第三边长是_____________.

【设计意图】问题1、2初步体会定理的价值;问题3针对学生可能出现的错误，分析强化对勾股定理条件的识别。

活动4：定理的文化与其他证法

【问题设计】

1.阐述定理的发现与证法发展过程。

2.毕达哥拉斯的发现。

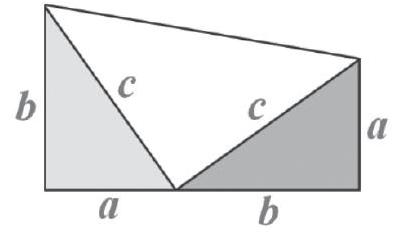
3.美国第20任总统加菲尔德用下图验证了勾股定理，你能做到吗？

4.大家可以去查询一些有趣的方法，或者你也可以想出某种方法。

【设计意图】回归教材，体会与本节课不同的知识获得方式：观察、猜想、验证，引出其他验证方法。

通过文化史介绍，体验前人发现定理的过程，感受数学文化的魅力，提高学习数学的兴趣;从名家证法的再现，进一步体会面积法，培养几何直观素养，渗透数形结合思想。

三、教学思考

数学课堂教学不但要传递数学知识，更应渗透数学学习方法、数学思想，指导学生如何学习、如何研究。

（一）尝试发现新知识的不同渠道

数学定理的发现经常采取“观察、实验、猜想、验证”的科学探究过程。这种探究过程往往建立在大量的实验基础之上，通过归纳得以发现。一旦实验数据太小，学生的敏感性不足，是难以发现的。

从特殊到一般，条件逐步弱化，找到事物的本质属性，这也是一种发现新知识的有效手段。本课例通过直角三角形已知两直角边，发现斜边的确定性，由特殊到一般，从具体的数值到字母，在任务驱动下，反思、整合解决问题的方法，找到图形的共性，获得定理。

（二）基于思维自然生长的教学逻辑

勾股定理的探究，由毕达哥拉斯的发现等入手，显然指向性太明确;在非等腰直角三角形中引入网格、构造正方形求斜边长，在教学中未必顺理成章。

本课例从学情出发，关注学生的认知发展水平和已有的知识经验，探究知识发生、发展的过程，引导学生探索新知识。以原有实数      的获得为基础，发现拼图的可行性，沿着这条线得到勾股定理，运用勾股定理，由应用价值转入文化史，在文化史中导入前人证法，在课堂小结中明晰学法，归结直角三角形的性质，提出定理的应用展望，为数学生成埋下种子。

（三）充分利用学科知识间的关联性

设计富有思维量的问题，灵活驾驭课堂，有指导地开放课堂，抓住学科知识间的关联，有助于培养学生的学习力和综合知识运用能力。

在引导学生进行直角三角形的研究中，类比迁移等腰三角形的学习，从边、角等几何元素入手，研究其性质、判定，了解几何学习的基本套路，为往后学习更多几何图形指明方向;教学过程渗透数形结合思想，以数解形，本意为推导勾股定理，实为解题指导;课堂小结延伸斜三角形，暗示勾股定理对几何运算的普适性。

本节课中，除了回顾实数      作为推进课堂教学的着力点，面积法作为运算手段，还涉及在特例中批判性地运用等腰三角形的“三线合一”，在运算过程中巩固了整式运算的有关知识。

（四）课堂教学成为学生情感态度价值观的载体

从学生学习的情感、态度来看，一个班级近五十个学生，他们对生活现象的敏感度也不同，相比勉为其难地“逼”学生发现问题，不如在定理的不经意获得中，培养学生观察、反思、深入的学习习惯，发现事物的规律，感受数学研究的获得感。

逻辑思维能力是指正确、合理思考的能力，而学生的学习与生活环境又影响了学生的逻辑思维，所以要求我们构建基于学生逻辑思维的课堂教学逻辑。

培养学生做学习的有心人，甚至是知识的发现者，其手段是多样的，可能是顿悟之后的发现与证明，也可能是解决问题过程中的自然生成。后一种方式在课堂教学中表现为：基于学生的认知基础，利用并开发教材，创设自然的发散思维情境，唤醒旧知识，引导学生通过联想、试错、整合，在问题的解决过程中，逐步弱化条件，探索并获得新知识。

参考文献：

[1] 卜以楼.基于四能的“勾股定理”教学创新设计[J]. 中学数学教学参考，2016（20）.

[2]林日福.基于思维自然生长的创新教学设计与思考：以“探索勾股定理”一课为例[J].中国数学教育，2018（21）.

（责任编辑：奚春皓）