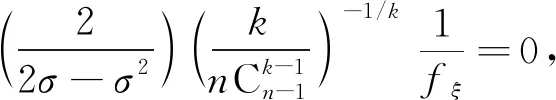一类k-Hessian方程径向k-容许解的存在性
段对花,高承华
(西北师范大学 数学与统计学院,兰州 730070)
1 引言与预备知识
k-Hession问题源于几何学、流体力学等应用学科[1]. 一般地,对一个有界域Ω⊂n和函数u∈C2(Ω),k-Hessian算子定义为
其中:λ(D2u)=(λ1,λ2,…,λn)是Hessian矩阵D2u的特征值向量,λ1,λ2,…,λn是特征值;Sk(λ(D2u))是第k阶初等对称多项式. 显然,k-Hessian算子是一类二阶完全非线性微分算子,是Hessian 矩阵D2u所有k×k阶主子式之和. 特别地,当k=1时,k-Hessian方程即退化为Laplace方程Δu=f[2-4]; 当k=n时,k-Hessian方程即退化为Monge-Ampère方程detD2u=f[5-7].
受上述结果启发,本文研究一类k-Hessian问题:
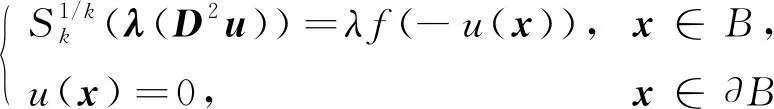
(1)
径向k-容许解的存在性,其中λ>0是一个参数,k=1,2,…,n,B={x∈n: |x|<1}是一个单位球.
定义1[9]设Ω⊂n是有界开集. 对k∈{1,2,…,n},函数u∈C2(Ω)是k-容许函数当且仅当λ(D2u)∈Γk,其中Γk={λ∈n:Sk(λ(D2u))>0,k=1,2,…,n}⊂n.
本文总假设:
(H1)f: [0,∞)→[0,∞)是连续的.
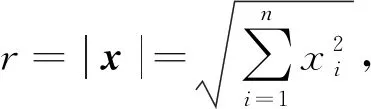
引理1[11]假设v(r)∈C2[0,1]是径向对称的函数,且满足v′(0)=0,则函数u(x)=v(r),r=|x|<1是C2(B)的,且有
因此,寻找问题(1)的径向对称解即等价于寻找问题
(2)
的解. 由文献[17]易知函数u∈C2(B)是问题(1)的径向k-容许解当且仅当v(r)是问题(2)的负解.
取函数φ∈C2[0,1],做变换φ=-v,有
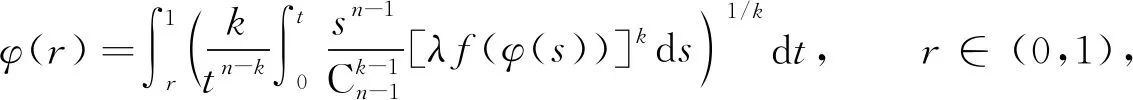
(3)
则u(|x|)=-φ(r)是问题(1)的径向k-容许解当且仅当φ(r)是积分方程(3)的一个正解.
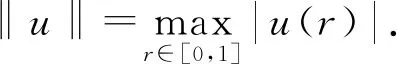

其中σ∈(0,1/2)是给定的一个正常数. 定义算子A:P→C[0,1]为

(4)
因为f: [0,∞)→[0,∞)是连续的,所以由Arzela-Ascoli定理易证A:P→P是全连续算子. 于是寻找问题(1)的径向k-容许解即等价于寻找算子A的不动点.
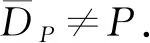
1) 若‖Au‖≤‖u‖,u∈∂DP,则iP(A,DP)=1;
2) 假设存在e∈P{θ},使得对所有的u∈∂DP和任意的μ>0,均有u≠Au+μe,则iP(A,DP)=0;

对给定的正实数σ,γ,定义
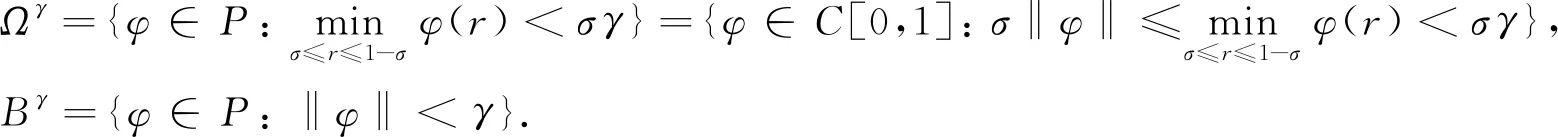
(5)
引理3[3]式(5)中定义的Ωγ和Bγ满足如下性质:
1)Ωγ是P中的开集;
2)Bσγ⊂Ωγ⊂Bγ;
4) 若φ∈∂Ωγ,则有σγ≤φ(r)≤γ,r∈[σ,1-σ].
2 主要结果
假设条件:
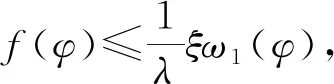

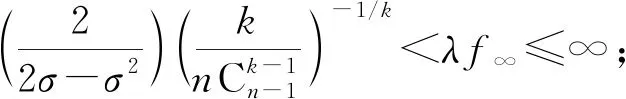
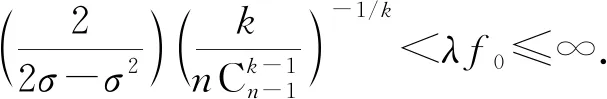
定理1假设条件(H1)~(H3)同时成立,则有:
(i) 若α<σβ,则积分方程(3)至少有一个正解φ(r),且满足

(ii) 若α>β>σβ,则积分方程(3)至少有一个正解φ(r),且满足

(6)
证明: 用引理2证明该结果,先证明引理2中的1),2)成立.
1) 由(H2)可知,对∀φ∈∂Bα和t∈[0,1],有
即‖Aφ‖≤‖φ‖,φ∈∂Bα. 由引理2中1)的结论可得iP(A,Bα)=1.
2) 取e(r)=1,则e∈P{θ}. 下证φ≠Aφ+μ,φ∈∂Ωβ,μ>0.
反证法. 假设结论不成立,则存在φ0∈∂Ωβ和μ0>0,使得φ0=Aφ0+μ0. 由引理3中4) 可知σβ≤φ0(r)≤β. 进一步结合引理3中3),可得

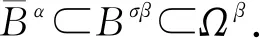

因此‖φ‖≤β,表明结论(i)成立.

为方便,记
定理2假设条件(H1)成立,若条件(H4)或(H5)之一成立,则问题(1)至少有一个径向k-容许解.
证明: 只证明(H4)成立的情形,(H5)成立的情形类似可证.
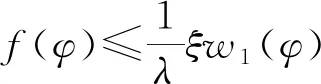
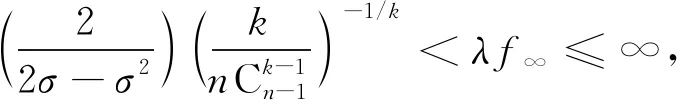
所以存在β>0,使得α<σβ,对任意的φ≥σβ,有

因此(H3)成立.
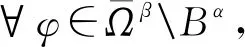
推论1假设条件(H1)成立,若
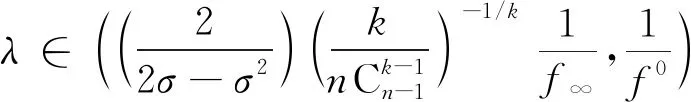
(7)
或者

(8)
成立,则问题(1)至少有一个径向k-容许解.
证明: 设ξ=0或ξ=∞. 当fξ=∞时,