CHFS:Complex hesitant fuzzy sets-their applications to decision making with different and innovative distance measures

Harish Garg|Tahir Mahmood| Ubaid ur Rehman| Zeeshan Ali

1Schoolof Mathematics,Thapar Institute of Engineering and Technology,Deemed University,Patiala,Punjab,India

2Department of Mathematics and Statistics,InternationalIslamic University,Islamabad,Pakistan

Abstract The objective of the authors is to establish an innovative concept of the complex hesitant fuzzy set(CHFS),which is the combination of the hesitant fuzzy set and the complex fuzzy set to manage complex and awkward information in the real-decision theory.The structure and the basic properties of the proposed set are studied in detail.Based on the internal structure of the set and to find the degree of the discrimination between the pairs of the CHFSs,the generalized distance measures and modified generalized distance measures are defined.Severalproperties and their relationship between them are derived in detail.Also,several cases of the proposed measures are exposed which reduce them to the existing studies.Furthermore,based on these proposed measures,a decision-making approach is established under the uncertain environment and several numerical examples are given to examine the feasibility and validity of the explored measures.Finally,the credibility of the modified and parameterized distance measures based on CHFSs is verified by comparing them with some existing measures.

1|INTRODUCTION

Multiple attribute decision-making(MADM)process includes the examination of a limited arrangement of options and positioning them as far as the fact that they are so trustworthy to decision-maker(s)when all the rules are thought of at the same time.In this procedure,the rating estimations of every option incorporate both exact information and specialists'subjective data.However,generally,it is expected that the data given by them are fresh in nature.In any case,because of the unpredictability of the framework step by step,the genuine contains numerous MADM issues where the data is either ambiguous,lose or dubious in nature.To manage it,a concept of fuzzy set(FS)[1]has been explored.To access the degree of discrimination between the pairs of the FSs,a concept of distance and similarity measures are a powerfultechnique.Both concepts are utilized in many places like decision-making[2]problems,pattern recognition[3],and medical diagnosis[4].Wang[5]utilized the similarity measures based on FS.FS contains the grade of membership limited to[0,1],as an important technique to describe the opinion of a human being in the form of grades.FS has received extensive attention in the last few decades[6–8].Recently,a fuzzy collaborative approach for examining the suitability of smart health was established by Chen et al.[9].The fuzzy counterparts of the Fischer diagonal condition in T-diverges space were explored by Jin et al.[10].Sanchez-Roger et al.[11]investigated the fuzzy logic and its uses in finance.For more work based on FS(refer[12,13]).

Many researchers raise a question,when the range of FS will be changed,which is the real number instead of the complex number from a unit disc in a complex plane,and what willbe the outcome of the effect.Ramot et al.[14]resolved this issue to explore the complex FS(CFS),which contains the grade of membership in the form of a complex number belonging to unit disc in a complex plane.CFS copes with the two-dimension information in a single set.CFS is an important technique to describe the opinion of a human being in the form of grades.CFS has received extensive attention in the last few years.Liand Chiang[15,16]explored the complex neuro-FS and their function approximation.The systematic review based on CFS and logic was established by Yazdanbakhsh and Dick[17].The notion of CFS is also established by Nguyen et al.[18],but the idea of Ramot et al.provides a wide range for decision-makers.Many researchers utilized CFS in different fields[19–21].

In some situations,when a decision-maker gives membership grades in the form of groups,it is very awkward for the FS to describe these types of problems.For coping such types of issues,Torra[22]explored the novelty of hesitant fuzzy set(HFS)containing the grade of membership in the formof a finite subset of[0,1].HFS is considered a more generalized technique to manage the awkward and critical types of information in FS theory.HFS has received extensive attention in the last few years.Furthermore,Weiet al.[23]investigated the entropy measures based on HFSs and their application in the multi-attribute group decision making(MAGDM)problem.The hesitant fuzzy linguistic preference relation was explored by Wu et al.[24].Liang et al.[25]pioneered the risk appetite dual hesitant fuzzy threeway decisions with TODIM(an acronym in Portuguese for Interative Multi-criteria Decision Making)methods.The diverge measures based on HFS was explored by Kobza et al.[26].Wang et al.[27]established the new distance measures for HFSs and their application to MAGDM.Due to its structure,many researchers utilized HFS in different fields[28,29].

Keeping in view of the importance of similarity measures(SMs),recently many researchers have chosen different SMs based on FS[30],CFS[31],and HFS[32].On the other hand,when a decision-maker gives complex-valued membership grades in the form of groups,the existing measures cannot solve exactly.For handling such kinds of issues and keeping the advantages of the SMs,here,the authors establish a complex hesitant fuzzy set(CHFS),which is the combination of the hesitant fuzzy set(HFS)and CFS.In CHFS theory,degrees of membership are complex-valued and are given in polar coordinates.All theories such as FS,CFS,and HFS worked impressively,when a decision-maker faced such type of data which contains two-dimensional information in a single-set.For instance,｛0.1ei2π（0.8）,0.5ei2π（0.2）,0.9ei2π（0.5）,0.3ei2π（0.9）｝,then the existing alltheories are unable to deal with such type of data.To deal with such type of issues,the CHFS is a perfect technique to sort out practical decision issues in the environment of FS theory.CHFS is more powerful and more general than existing theories like FS,CFS,and HFS to cope with awkward and complicated data in real-life decisions.Since all theories are special cases of the interpreted CHFS,the edges of the interpreted CHFS are examined below:

(1)If we let the imaginary parts of the CHFS as zero,then the CHFS is converted into HFS which is in the shape of{0.1,0.5,0.9,0.3}.

(2)If we let the CHFS as a singleton set,then the CHFS is converted into CFS which is in the shape of｛0.1ei2π（0.8）｝.

(3)If we let the CHFS as a singleton set and the imaginary parts as zero,then the CHFS is converted into FS which is in the shape of{0.1}.

Further,the generalized distance measures(GDMs)and modified GDMs(MGDMs)based on established approaches are utilized and also expose the specialcases of the established approach.After this,the parameterized distance measures are established and their particular cases are discussed.The established measures are utilized in the environment of decision making to examine the feasibility and validity of the explored measures.Moreover,the numerical examples for established measures are solved to express the superiority and integrity of the explored work.Finally,to evaluate the credibility of the modified and parameterized distance measures based on CHFS,they are verified by comparing them with some existing measures.

The main contributions of this article are as follows:

1.Based on existing concepts,firstly we establish the CHFS,which is the combination of the HFS and the CFS,to manage complex and awkward information in real-decision theory.

2.Based on existing distance and SMs called modified distance measures taken from[33],we established(GDMs)and(MGDMs)and discussed their particular cases.

3.After this,based on existing distance and SMs,and parameterized distance measures taken from [34],we established the parameterized distance measures and their particular cases.

4.The established measures are utilized in the environment of decision making to examine the feasibility and validity of the explored measures.Moreover,the numerical examples for established measures are solved to express the superiority and integrity of the explored work.Finally,to evaluate the credibility of the modified and parameterized distance measures based on CHFS,they are verified by comparing with some existing measures.

The article is arranged as follows:In Section 2,we revised the basics notions and their properties are discussed.In Section 3,based on existing concepts,we established the idea of CHFS and discussed its fundamental laws.In Section 4,the modified and parameterized distance measures based on the established concepts are investigated.In Section 5,the established measures are utilized in the environment of decision making to examine the feasibility and validity of the explored measures.Moreover,the numerical examples for established measures are solved to express the superiority and integrity of the explored work.Finally,to evaluate the credibility of the modified and parameterized distance measures based on CHFS,they are verified by comparing with some existing measures.The conclusion of this article is exposed in Section 6.

2|PRELIMINARIES

This section discusses some basic theories related to FSs,CFSs,and HFSs and their fundamental properties are derived.Throughout this articleXrepresents a fix set.

Definition1[1]A FSQis of the form:

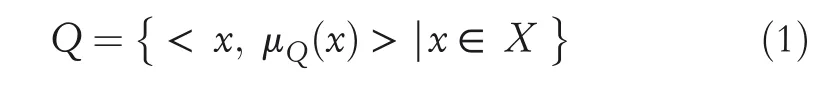
with a condition 0≤μQ（x）≤1,whereμQ（x）represents the grade of truth.The pairQ=＜x,μQ（x）＞is called the fuzzy number.Throughout this article,the collection of allFSs onXis denoted byFS(X).

Definition2[1]Let P,Q∈FS(X)Then the basic operations are defined as

1.Pc=｛＜x,1-μP（x）＞|x∈X｝.

2.P∩Q=｛＜x,min｛μP（x）,μQ（x）｝＞|x∈X｝.

3.P∪Q=｛＜x,max｛μP（x）,μQ（x）｝＞|x∈X｝.

Definition3[14]A CFSQis of the form:

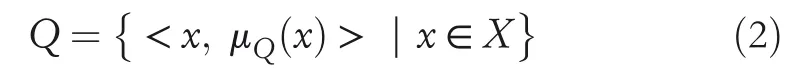
whereμQ（x）=γQ（x）.ei2π（ωγQ（x））represents the complexvalued truth grade in the form of polar coordinate,whereγQ（x）,ωγQ（x）∈[0,1].Furthermore,the pairQ=＜x,γQ（x）.ei2π（ωγQ（x））＞is called the complex fuzzy number(CFN).

Definition4[14] For any two CFNsP=＜

x,γP（x）.ei2π（ωγP（x））＞andQ=＜x,γQ（x）.ei2π（ωγQ（x））＞,then

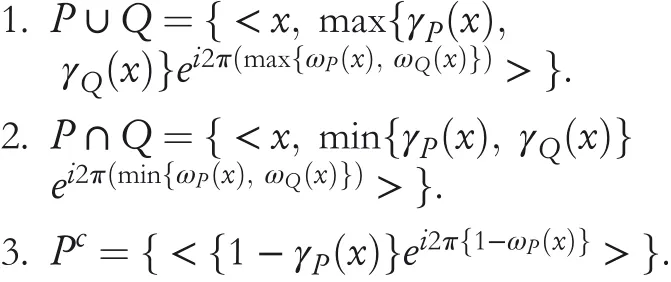
Definition5[22]A hesitant fuzzy number(HFN)Qis of the form:

whereμQ（x）is the set of different finite values in[0,1]representing the grade of truth for each elementx∈X.Further,the pairQ=＜x,μQ（x）＞is called HFN.

Definition6[22] LetP=＜x,μP（x）＞ andQ=＜x,μQ（x）＞are two HFNs.Then the basic operations are defined as

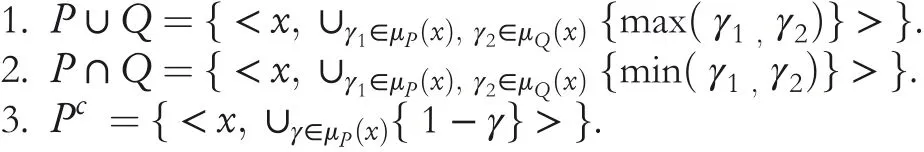
3|COMPLEX HESITANT FUZZY SETS

Here,we explore the notion of CHFSs and their basic operationallaws.The established work is also verified with the help of some numericalexamples.

Definition7A CHFSQis of the form:

Definition8LetP=（x,γPj（x）.ei2π（ωγPj（x）））andQ=be two CHFNs.Then

The theory of CHFS makes it a wide range effective technique to deal with awkward and complicated data in practicaldecision problems.The CHFS holds the grade of the membership in the shape of a subset of the unit disc in the complex plane,whose entities are in the shape of polar coordinates.Fundamentally,the CHFS holds two-dimension data in a single set.The interpreted CHFS is more general than existing theories like FS,CFS,and HFS,whose reasons and explanation are examined as follows.In CHFS,membership degree is complex-valued and is represented in polar coordinates.The amplitude term corresponding to the membership degree gives the extent of belongings of an object in a CHFS,and the phase term associated with the membership degree gives the additionalinformation,generally related with periodicity.The phase terms are novel parameters of the membership degree,and these are the parameters that distinguish the traditional FS,CFS and HFS theory.HFS theory deals with only one dimension at a time,which results in information loss in some instances.

In Definitions(7)and(8),when we assume the imaginary parts as zero,then the explored theory is transformed for HFS,which is described by Torra[22].Likewise,when we assume the CHFS as a singleton set,then the CHFS is transformed for CFS,which is described by Ramot et al.[14].Moreover,when we assume the CHFs as a singleton set and the imaginary part is zero,then the CHFS is transformed for FS,which is defined by Zadeh[1].

Example1Let

be two CHFSs.Then the operational laws of the Definition 8 are stated as follow as:

4|PROPOSED DISTANCE MEASURES USING COMPLEX HESITANT FUZZY SETS

In this portion we defined some distance measures for CHFSs.

Definition9LetPandQbe two CHFSs on setX.Then distance measure betweenPandQis designated bydc（P,Q）,which satisfies the following properties:

Definition10LetPandQbe two CHFSs on setX.Then SM betweenPandQis designated bysc（P,Q）,which satisfies the following properties:

Remark1

1.Ifdcis the distance measure between two CHFSsPandQ,thensc（P,Q）=1-dc（P,Q）is the SM between CHFSsPandQ.

2.Ifscis the SM between two CHFSsPandQ,thendc（P,Q）=1-sc（P,Q）is the distance measure between CHFSsPandQ.

Definition11LetPandQbe two CHFSs on setX.Then generalized complex hesitant normalized distance(GCHND)is defined as follows:

whereλ＞0.

Theorem1TheGCHNDsatisfiesthefollowingthree properties

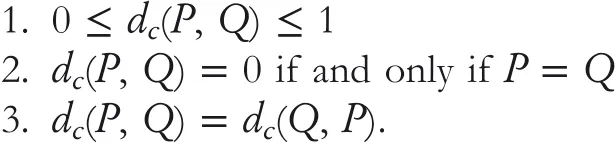
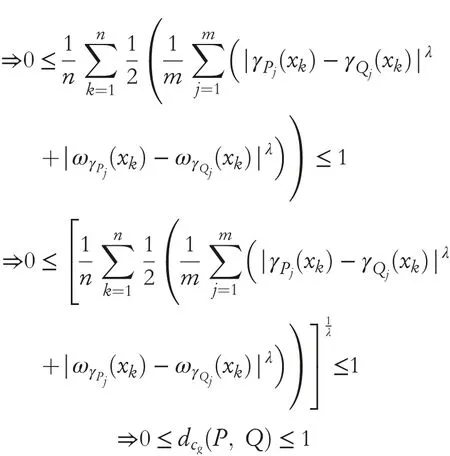
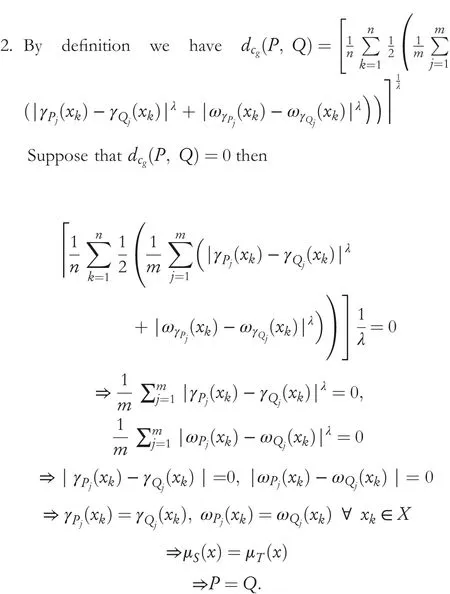
Conversely suppose thatP=Qthen

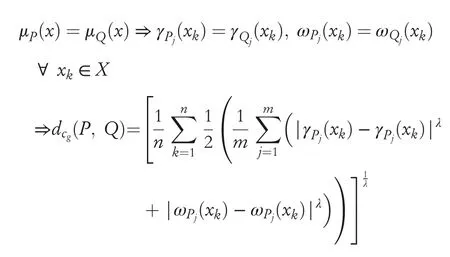
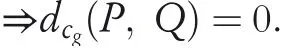
Remark2

1.Ifλ=1,then GCHND become a Hamming complex hesitant normalized distance(HCHND)betweenPandQi.e.

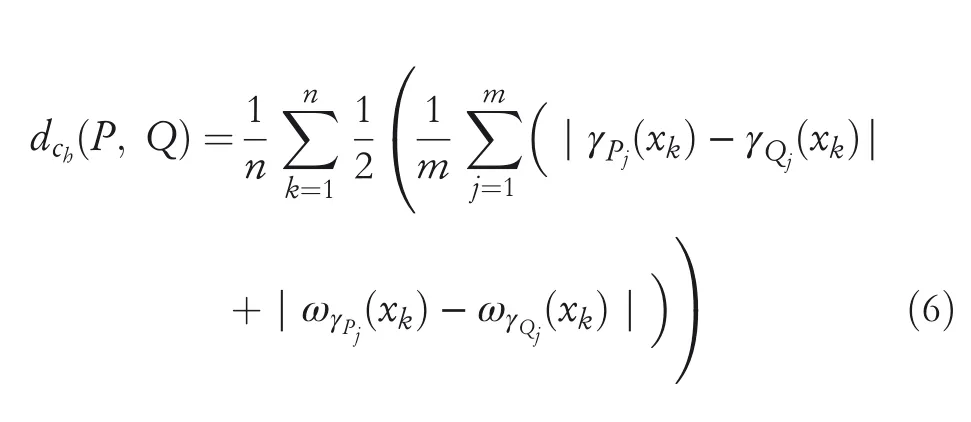
2.Ifλ=2 then GCHND become an Euclidean complex hesitant normalized distance(ECHND)betweenPandQthat is,

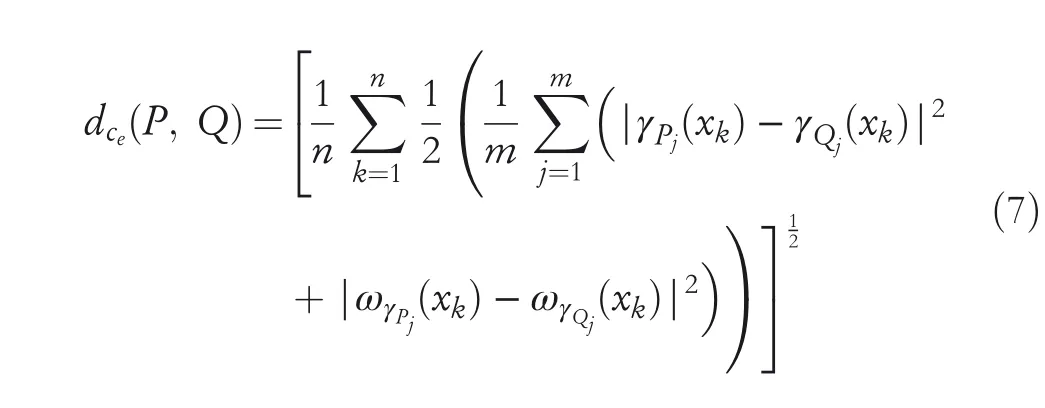
Definition12LetPandQbe two CHFSs on setXandwkbe a weight for eachx∈Xsuch thatThen,weighted generalized complex hesitant normalized distance(WGCHND)are defined as follows

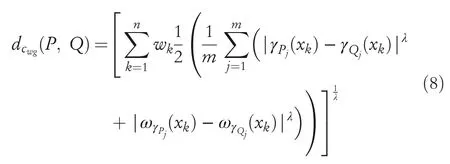
whereλ＞0.

Remark3 1.Ifλ=1 then WGCHND become the weighted Hamming complex hesitant normalized distance(WHCHND)betweenPandQthat is,

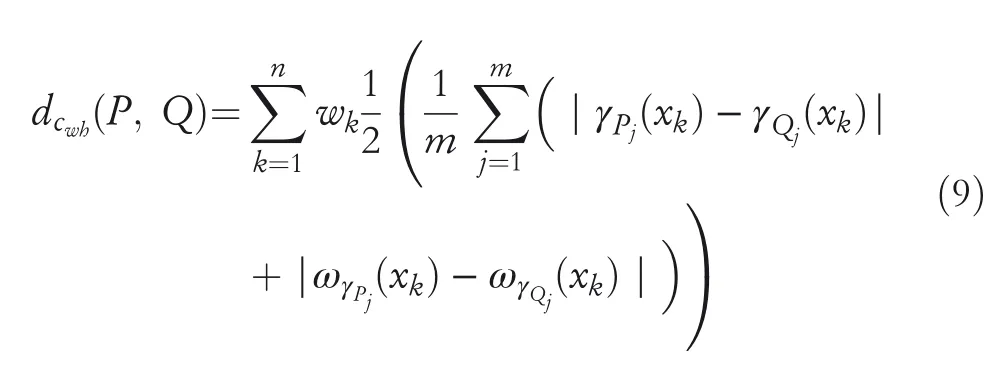
2.Ifλ=2 then WGCHND become the weighted Euclidean complex hesitant normalized distance(WECHND)betweenPandQthat is,

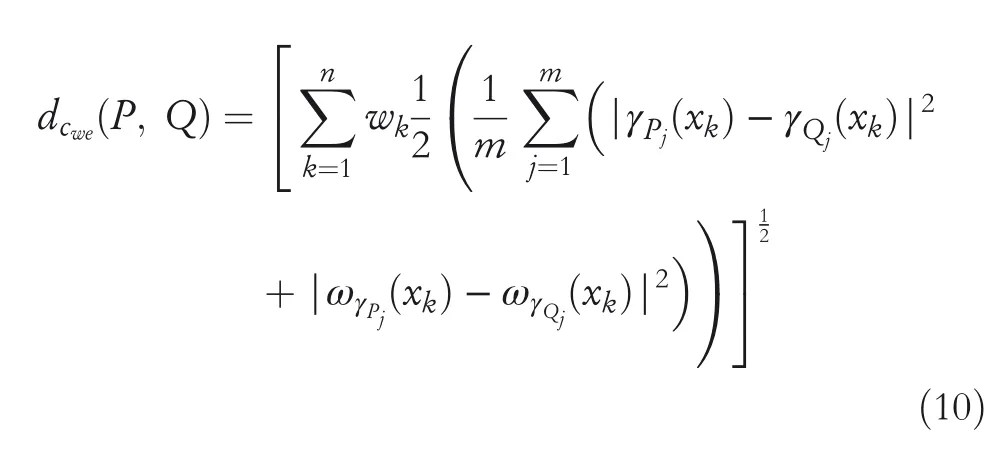
Definition13LetQbe a CHFS onX={x1,x2,x3,…,xn}.Then for anyxk∈X,m（μQ（xk））is the length ofμQ（xk）.We define the hesitant degree ofand the hesitant degree ofQis defined as

Definition14LetPandQbe two CHFSs on setX.Then we defined GCHND including the hesitant degree betweenPandQas

whereλ＞0.

Remark4 1.Ifλ=1,then GCHND including hesitant degree become HCHND including the hesitant degree betweenPandQthat is,

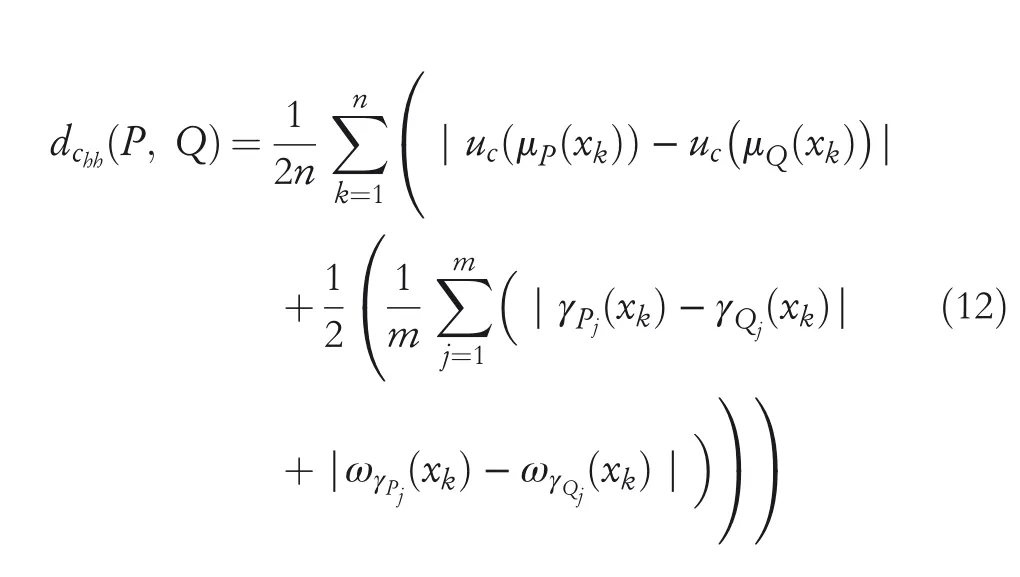
2.Ifλ=2,then GCHND including the hesitant degree become ECHND including the hesitant degree betweenPandQthat is,

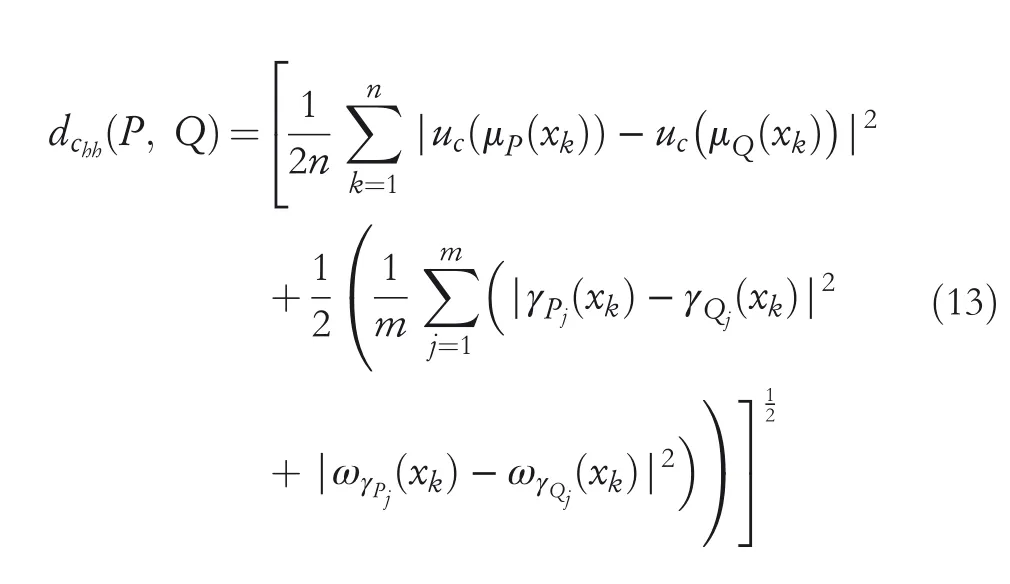
Definition15LetPandQbe two CHFSs onXandwkbe a weight for eachxk∈Xsuch that.Then we defined WGCHND including the hesitant degree betweenPandQas

Remark5 1.Ifλ=1,then WGCHND including the hesitant degree become WHCHND including hesitant degree betweenPandQthat is,

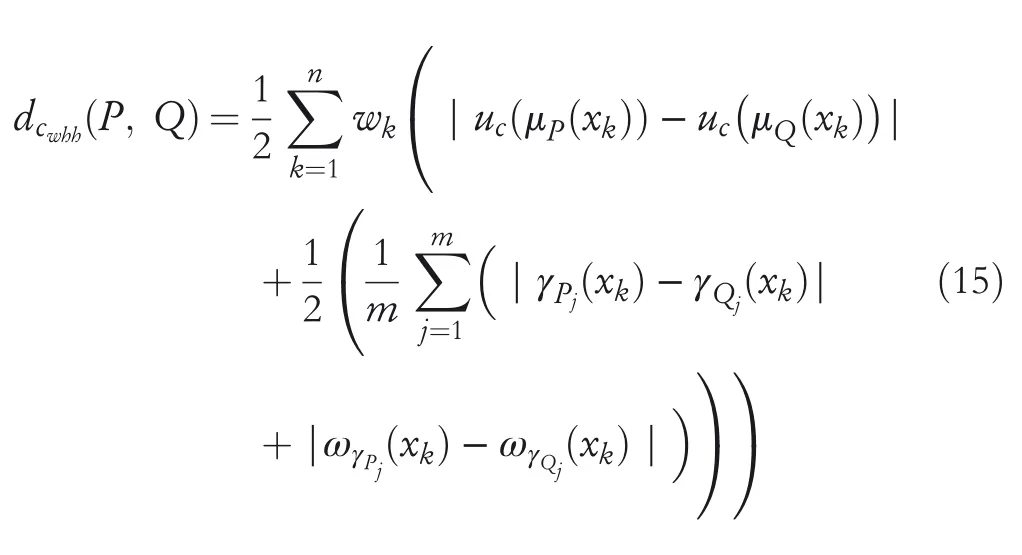
2.Ifλ=2 then WGCHND including hesitant degree become WECHND including hesitant degree betweenPandQthat is,

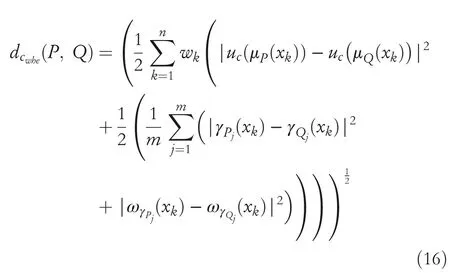
If we consider different preference between the hesitance degrees and the membership values then the distance measures are defined as

Definition16LetPandQbe two CHFSs onX.Then we defined GCHND including hesitant degree with preference betweenPandQas

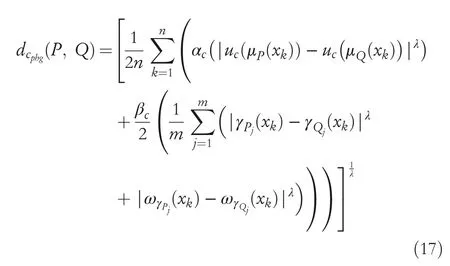
whereλ＞0,0≤αc,βc≤1 andαc+βc=1.Remark6 1.Ifλ=1,then GCHND including hesitant degree with the preference become HCHND including hesitant degree with the preference betweenPandQthat is,

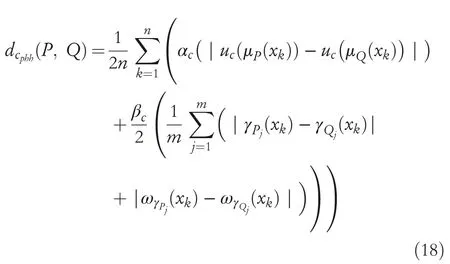
2.Ifλ=2 then GCHND including hesitant degree with preference become ECHND including hesitant degree with preference betweenPandQthat is,

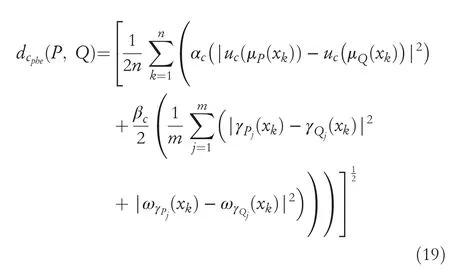
whenαc=0,it means that we are not considering the hesitance degree anddcphg,dcphh,anddcphe,become distance measuresdcg,dchanddce,respectively.

Definition17LetPandQbe two CHFSs onXandwkbe a weight for eachxk∈X.such that

Then we defined WGCHND including hesitant degree with preference betweenPandQas

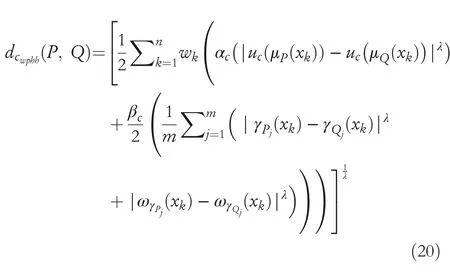
Remark7 1.Ifλ=1,then WGCHND including hesitant degree with the preference become WHCHND including hesitant degree with the preference betweenPandQthat is,

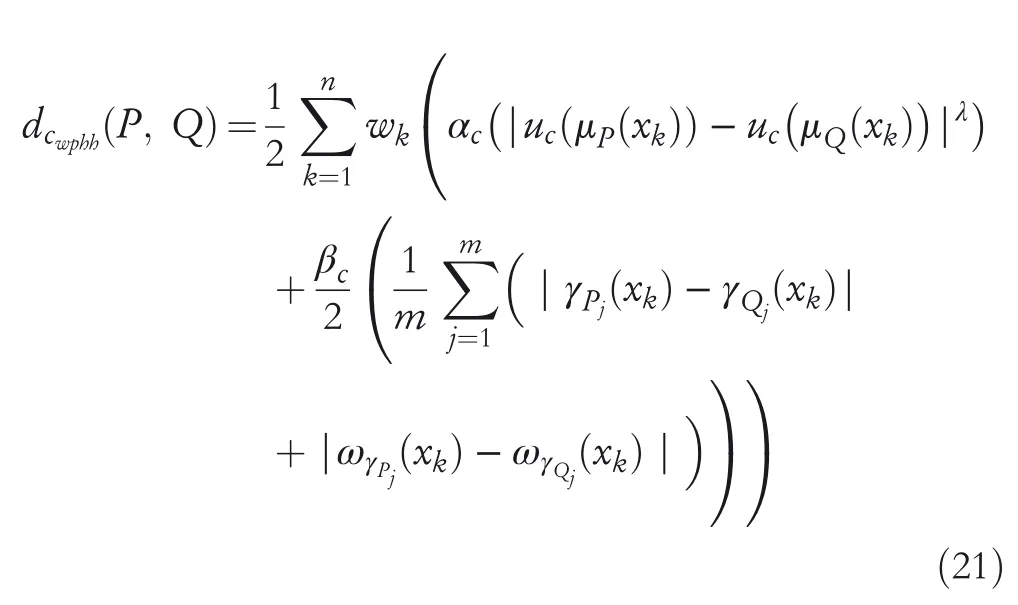
2.Ifλ=2,then GCHND including hesitant degree with preference become ECHND including hesitant degree with preference betweenPandQthat is,

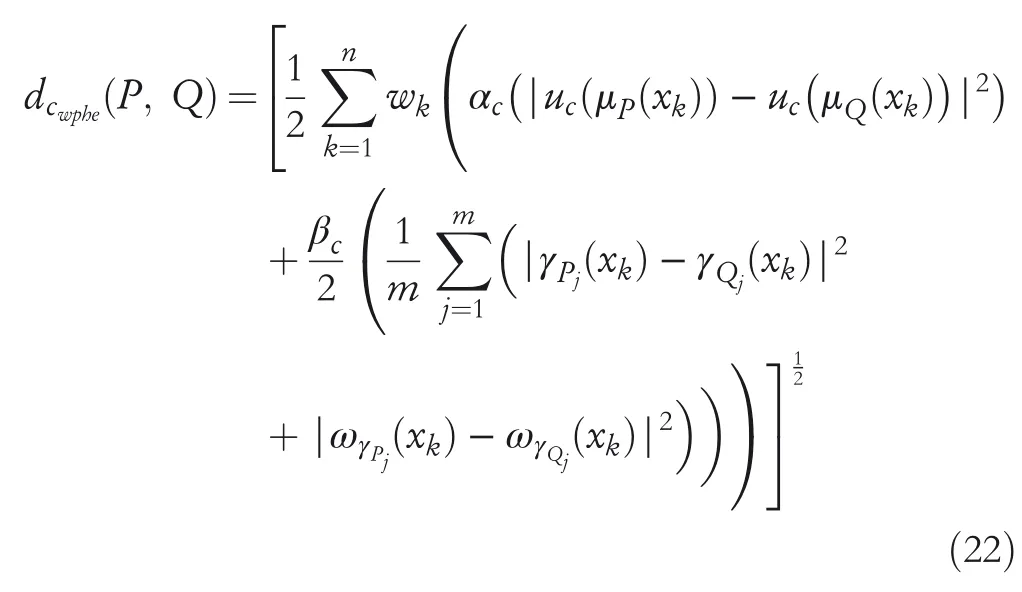
Definition18LetPandQbe two CHFSs onX.Then we defined modified generalized complex hesitant normalized distance(MGCHND)betweenPandQas follows

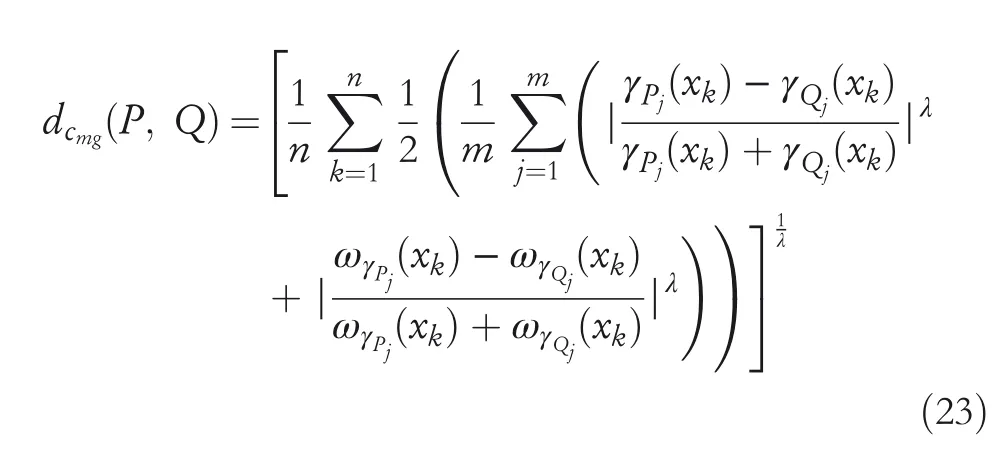
whereλ＞0.

Remark8 1.Ifλ=1,then MGCHND become themodified Hamming complex hesitant normalized distance(MHCHND)betweenPandQthat is,

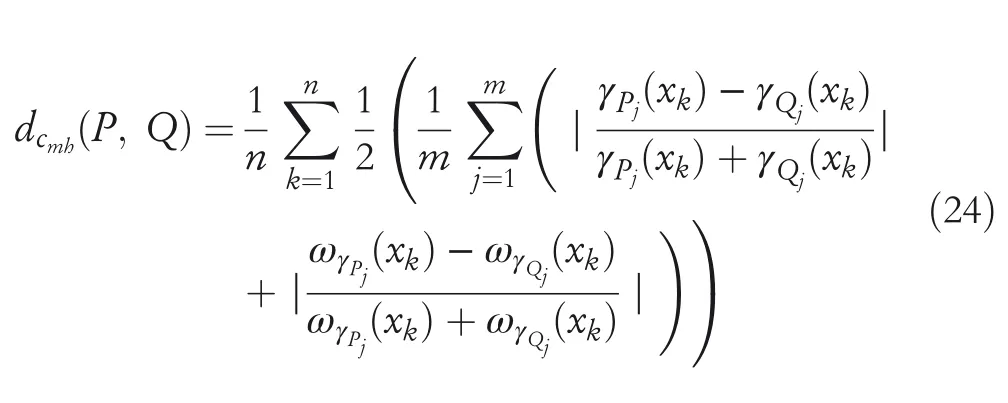
1.Ifλ=2,then MGCHND become modified Euclidean complex hesitant normalized distance(MECHND)betweenPandQi.e.

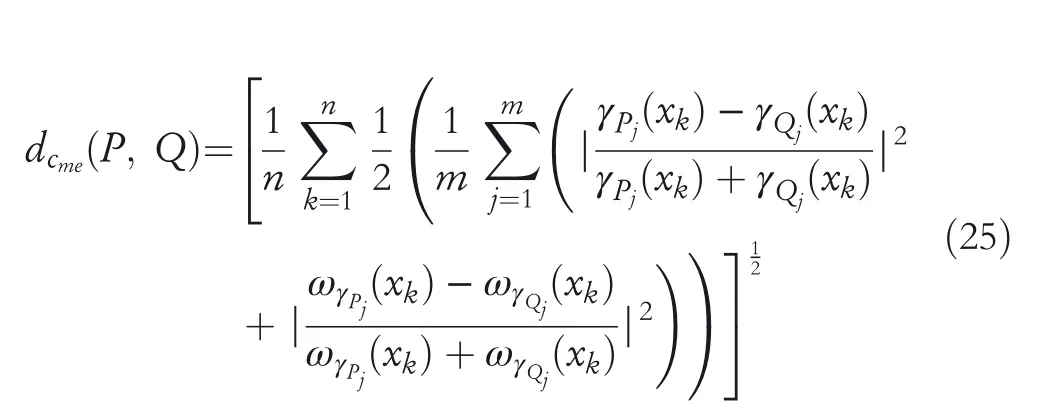
Definition19LetPandQbe two CHFSs onXandwkbe a weight for eachxk∈Xsuch thatThen we defined modified generalized complex hesitant normalized distance(MWGCHND)betweenPandQas follows

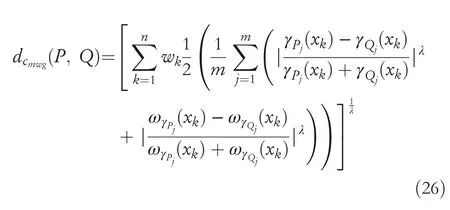
whereλ＞0.Remark9 1.Ifλ=1,then MWGCHND become modified weighted Hamming complex hesitant normalized distance(MWHCHND)betweenPandQthat is,

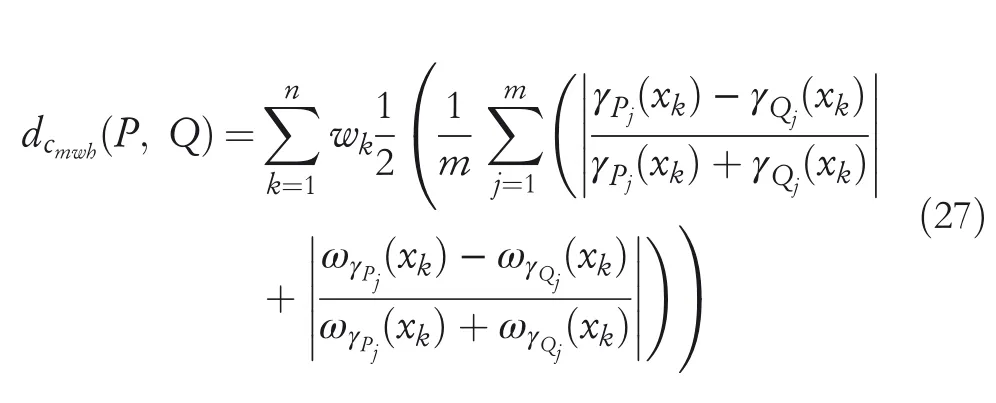
2.Ifλ=2,then MWGCHND become modified weighted Euclidean complex hesitant normalized distance(MWECHND)betweenPandQi.e.

Definition20LetQbe a CHFS onX={x1,x2,x3,…,xn}.Then for eachxk∈X,m（μQ（xk））is the cardinal number ofμQ（xk）.The credibility factor ofμQ（xk） is given ascc（μQ（xk））=（m（μQ（xk）））-1.Now letPandQbe two CHFS.Then the credibility factor betweenQandPis defined as

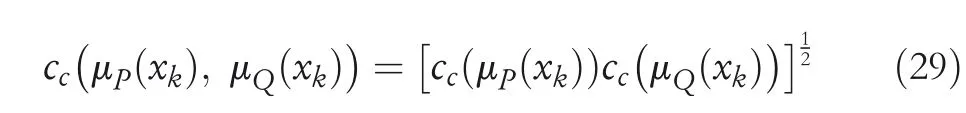
and normalized credibility factor is defined as:

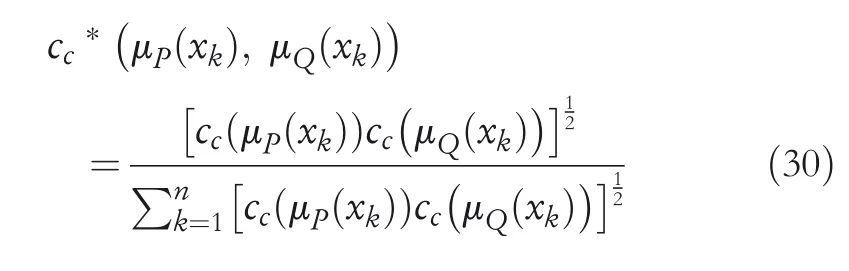
Now we define novel distance measures using credibility factor.

Definition21LetPandQbe two CHFSs onX.Then we defined the novel GCHND betweenPandQas:

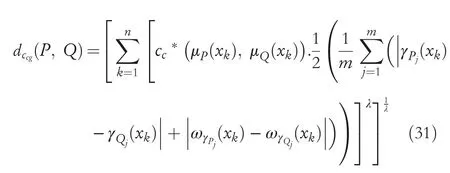
whereλ＞0.

Remark10 1.Ifλ=1,then the novel GCHND become novel HCHND betweenPandQas:

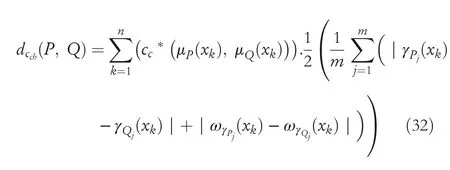
2.Ifλ=2,then the novel GCHND become novelECHND betweenPandQas:

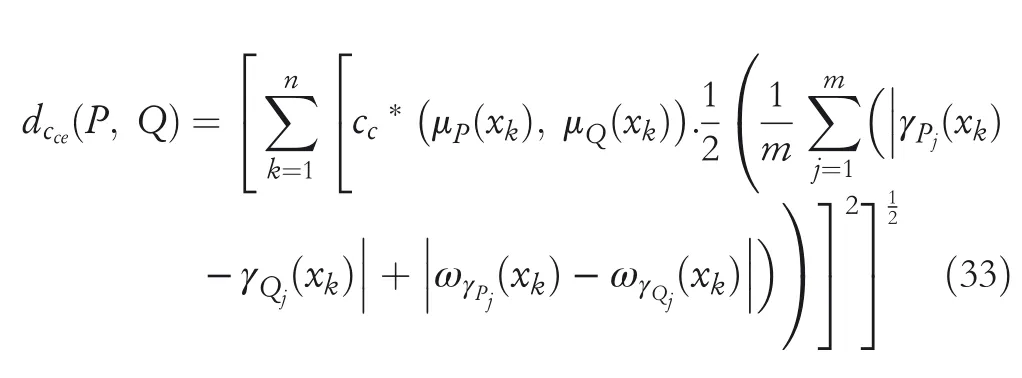
Definition22LetPandQbe two CHFSs onXandwkbe a weight for eachxk∈Xsuch thatand 0≤wk≤1.Then we defined the novel WGCHND as follows:

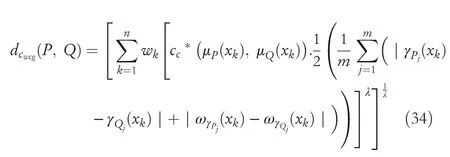
whereλ＞0.

Remark11 1.Ifλ=1,then the novel WGCHND become novel WHCHND betweenPandQas:

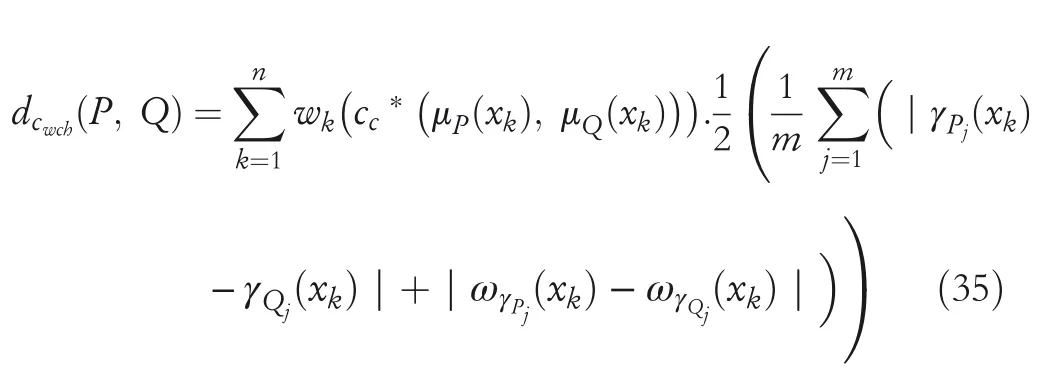
2.Ifλ=2,then the novel WGCHND become novel WECHND betweenPandQas

For the deep understanding of the relationship between the cardinalities and the values of CHFSs,we consider the conservative factorαccand the risk factorβcc.By using these factors,the above defined novel weighted distance measures become

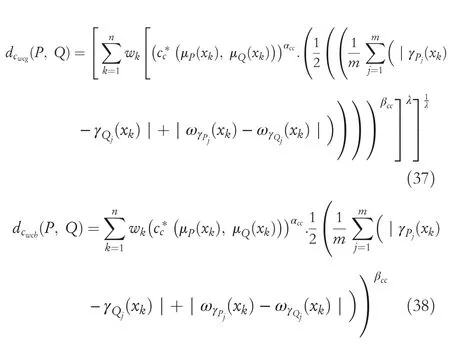
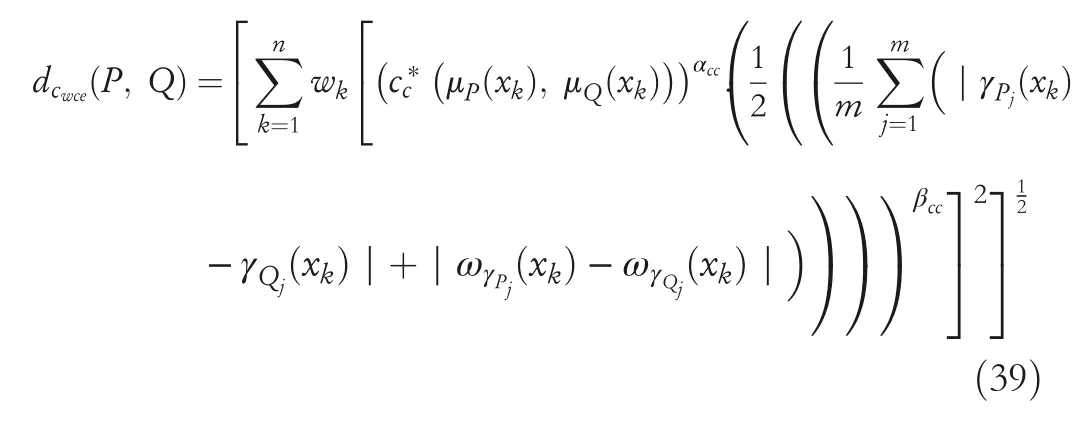
whereαcc,βcc∈[0,1]andαcc+βcc=1.

5|APPLICATIONS

Here,we applied the proposed distance measure to the environment of CHFSs to show the usefulness and effectiveness of the proposed distance measures.

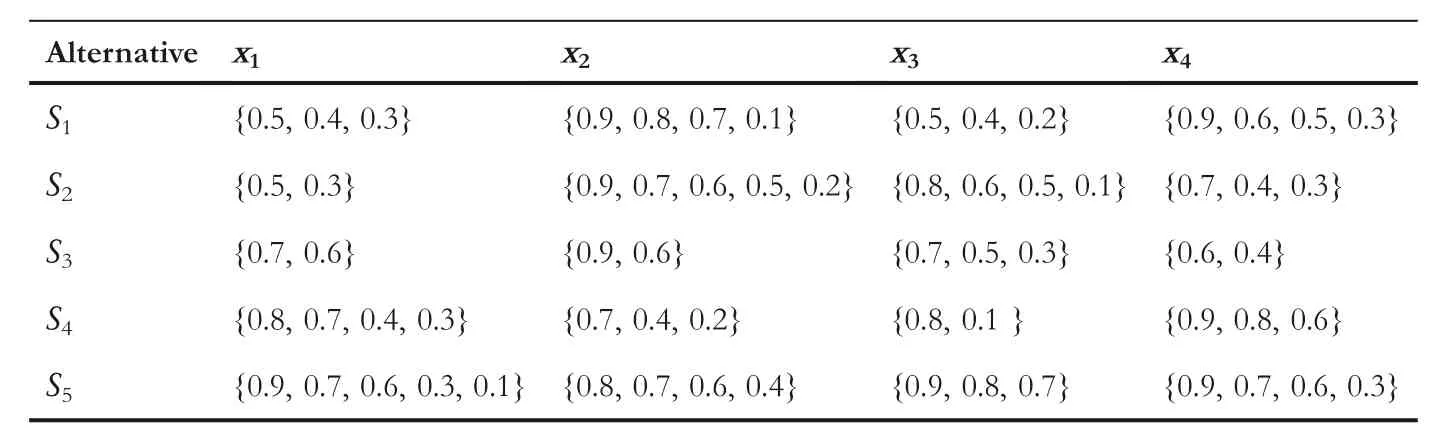
Example2For every society,energy is a crucial factor for the socio-economic development.Thus the accurate energy strategy accomplishes economic development and environment,and so,the most suitable energy strategy selection is crucial.Suppose five energy projects represented by

Sj(j=1,2,3,4,5)are to be invested.In the meantime,consider four attributes that are given as technological(x1),environmental(x2),socio-political(x3),and economic(x4).Consider the weight for attributes asW=(0.15,0.3,0.2,0.35).After this,a batch of experts is invited to assess the performance of the five alternatives with the respect to four attributes on the notion of excellence.By using CHFSs,the assessment results are gained as Table 1.

Suppose an ideal alternative isS*=｛＜x1,｛1ei2π（1）｝＞,＜x2,｛1ei2π（1）｝＞,＜x3,｛1ei2π（1）｝＞,＜x4,｛1ei2π（1）｝＞ ｝.If the length of CHFEs is not equal,we add the value 0.0ei2π（0.0）to the CHFE which is shorter in length until the length becomes equal.By taking（αcc,βcc）=（0.9,0.1）,（0.7,0.3）,（0.5,0.5）,（0.3,0.7）,（0.1,0.9）andλ=1,2,6,10,respectively,and the deviations between each alternative and ideal alternative are shown in Tables 2–6.

The graphicalinterpretation for the values in Table 5.

When we change the values of parameters,the alternative ranking order changes and for（αcc,βcc）=（0.9,0.1）the ranking of the proposed distance measures is given in Table 2,for（αcc,βcc）=（0.7,0.3）the ranking of the proposed distance measures is given in Table 3,for（αcc,βcc）=（0.5,0.5）the ranking of the proposed distance measures is given in Table 4,for（αcc,βcc）=（0.3,0.7）the ranking of the proposed distance measures is given in Table 5,and for（αcc,βcc）=（0.1,0.9）the ranking of the proposed distance measures are given in Table 6.As a result,decision-makers with different subjective preferences can select certain parameters according to their experiences and point of view.It indicates that the proposed parameterized distance measures are useful for the combination of subjective and objective decision-making information.

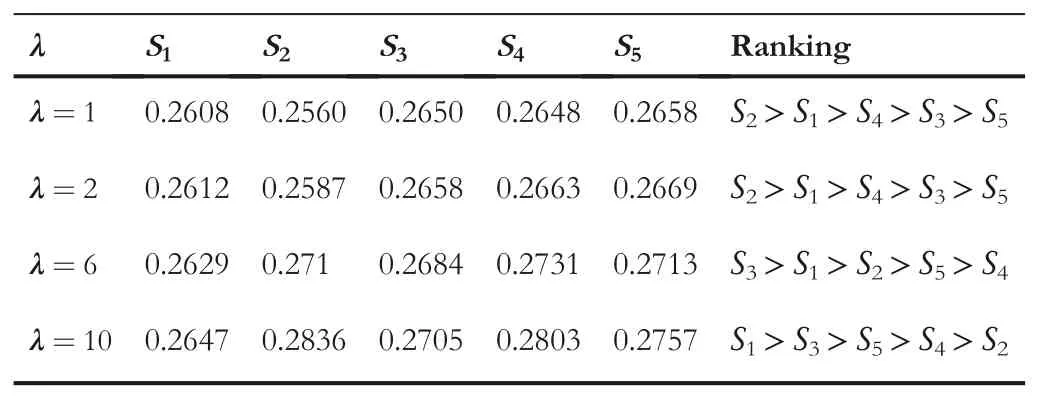
TABLE 2 Deviation between each alternative and ideal alternative and(αcc,βcc)=(0.9,0.1)

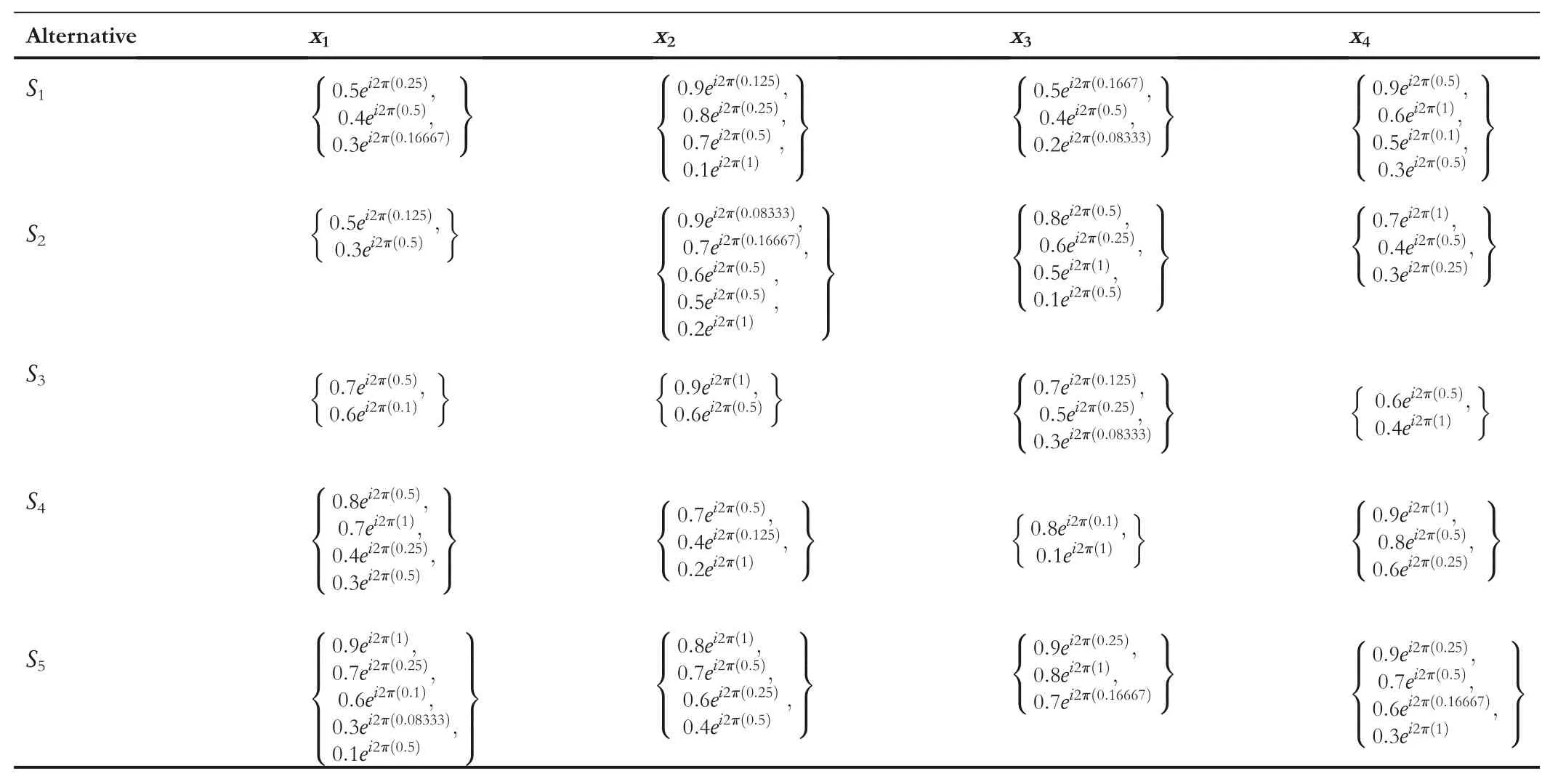
TABLE 1 Complex hesitant fuzzy decision matrix

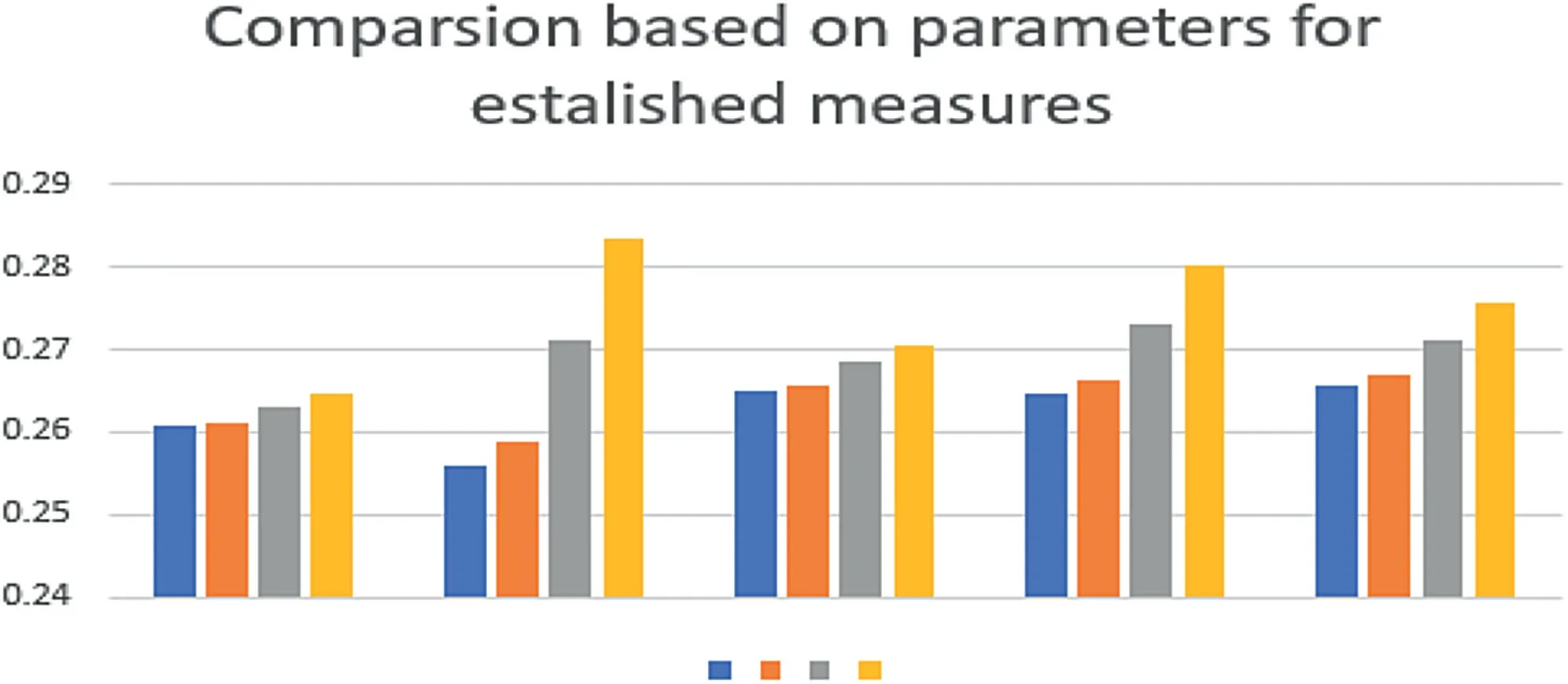
FI GURE 1 Graphical interpretation of the Table 2 results

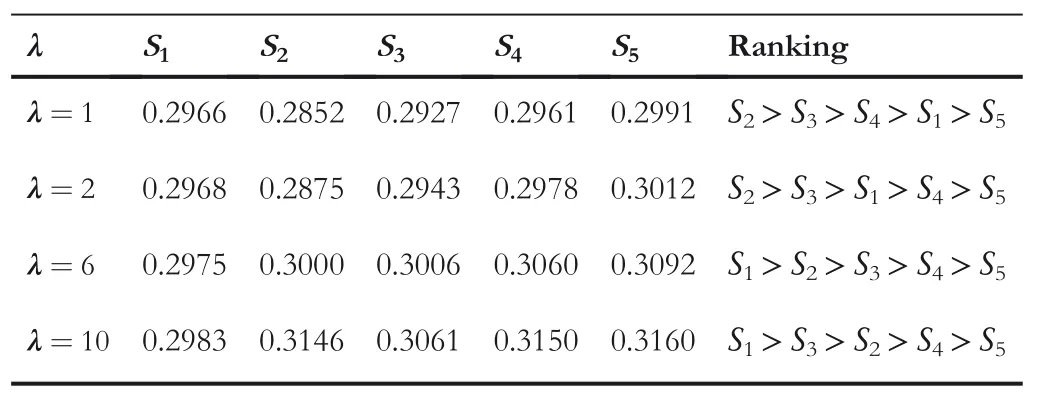
TABLE 3 Deviation between each alternative and ideal alternative and(αcc,βcc)=(0.7,0.3)

FI GURE 2 Graphical interpretation of the established work for different values of parameters

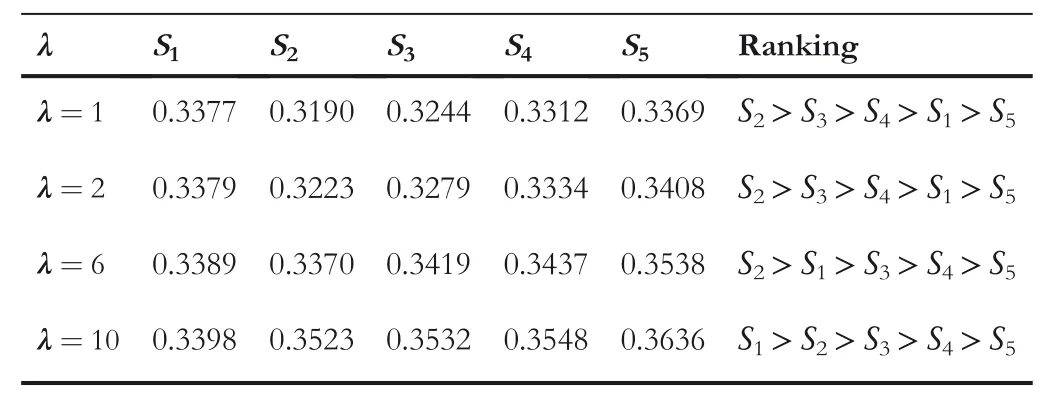
TABLE 4 Deviation between each alternative and ideal alternative and(αcc,βcc)=(0.5,0.5)

FI GURE 3 Graphical interpretation of the established work for different values of parameters

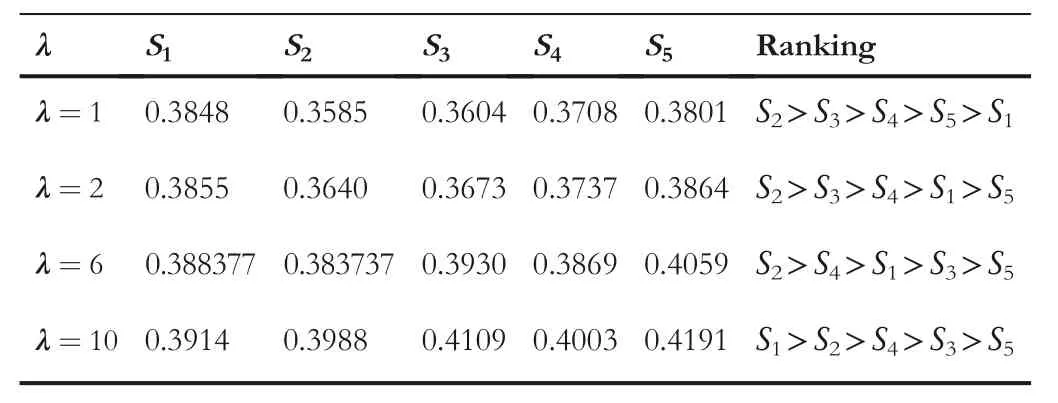
TABLE 5 Deviation between each alternative and ideal alternative and(αcc,βcc)=(0.3,0.7)

F I GURE 4 Graphicalinterpretation of the established work for different values of parameters

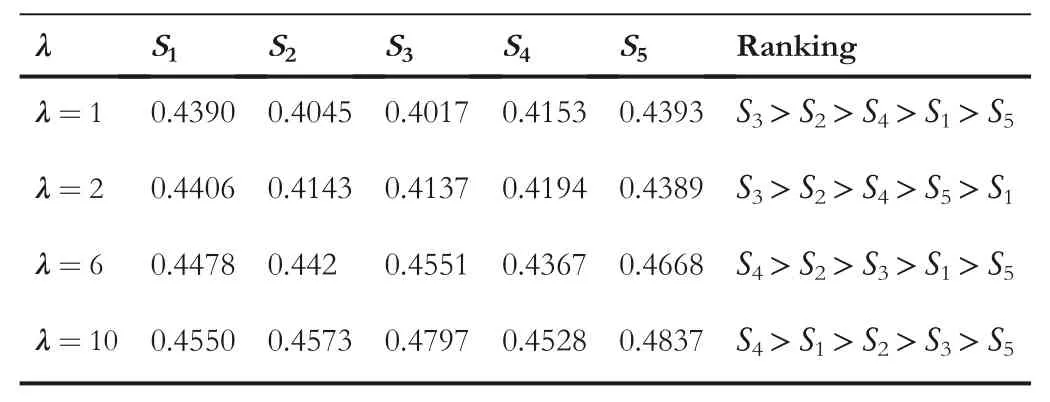
TABLE 6 Deviation between each alternative and ideal alternative and(αcc,βcc)=(0.1,0.9)

F I GURE 5 Graphicalinterpretation of the established work for different values of parameters

TAB L E 7 Hesitant fuzzy decision matrix

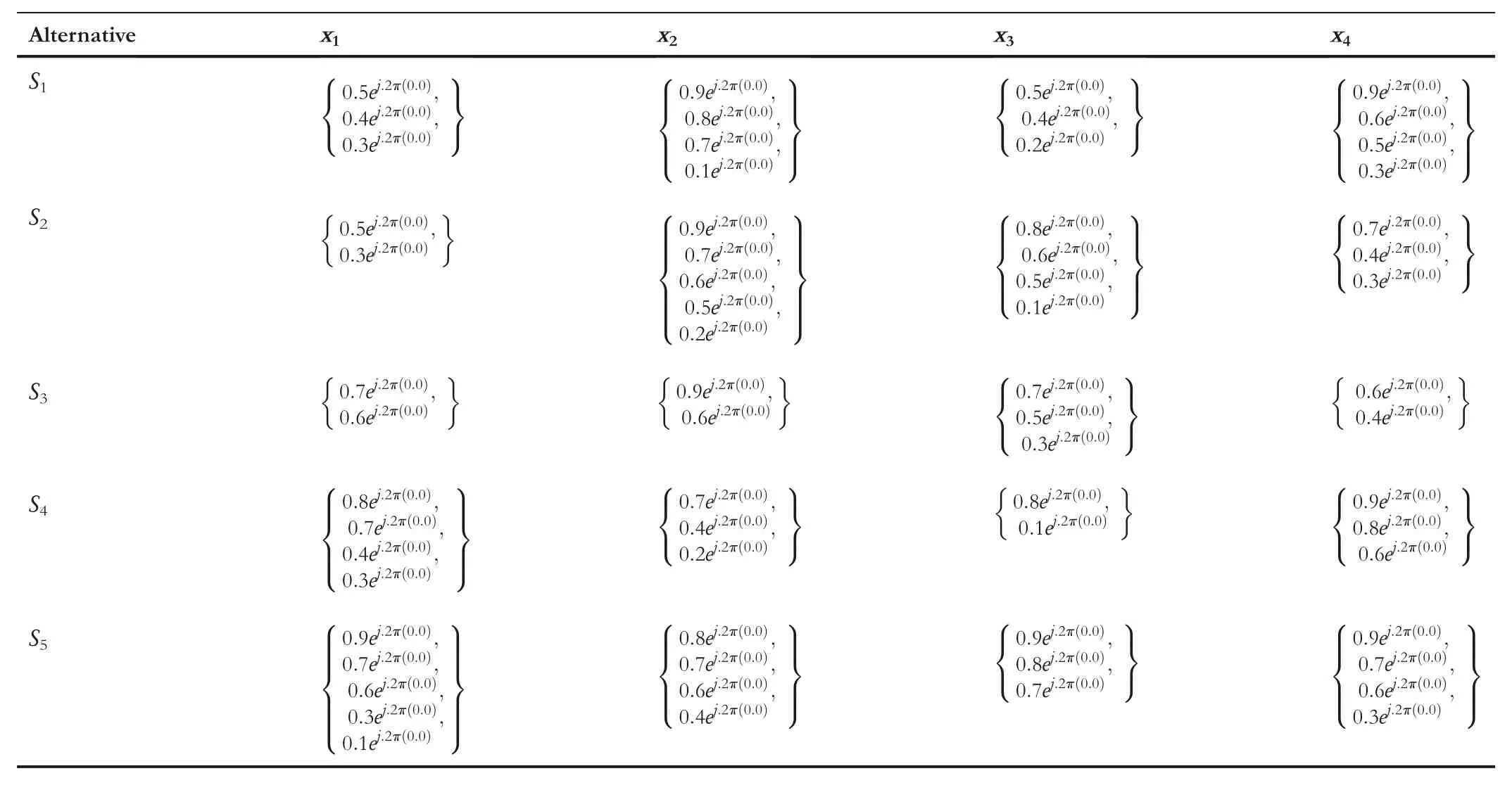
TABLE 8 Complex hesitant fuzzy decision matrix

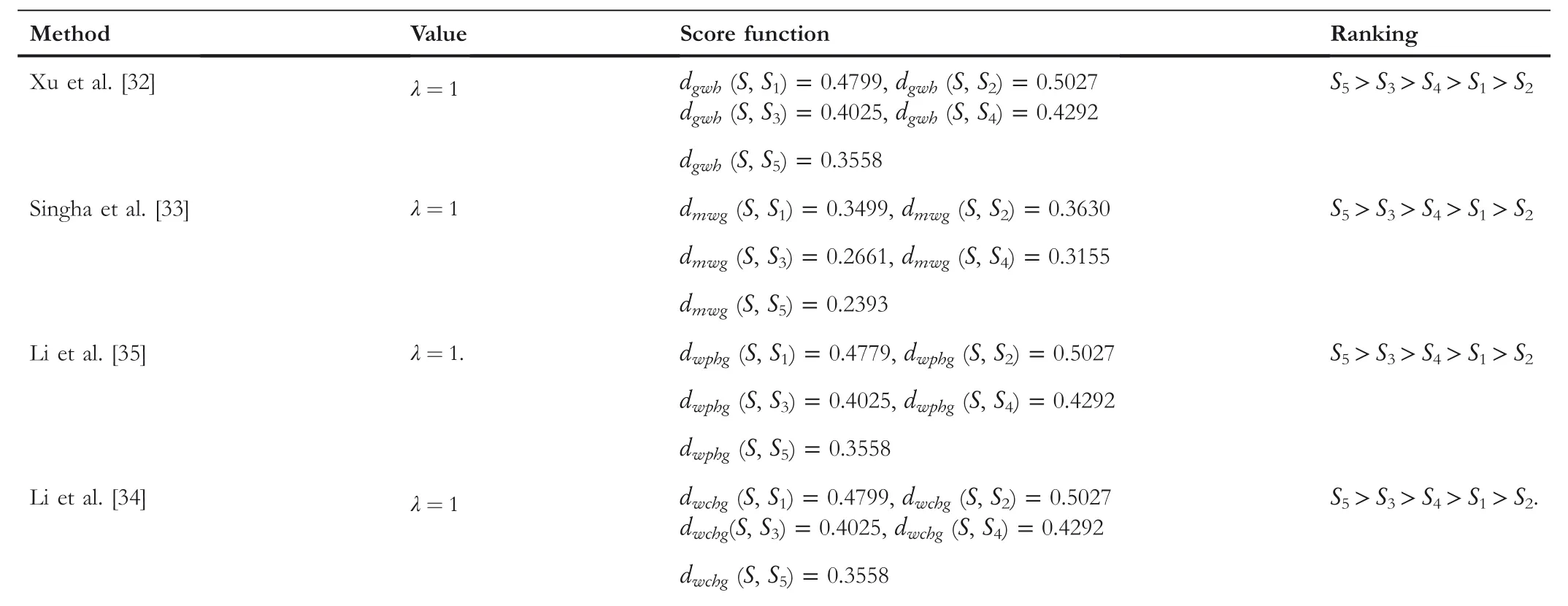
TABLE 9 Comparison between the proposed method and existing methods for Example 3 with parameter(αcc,βcc)=(0,1)

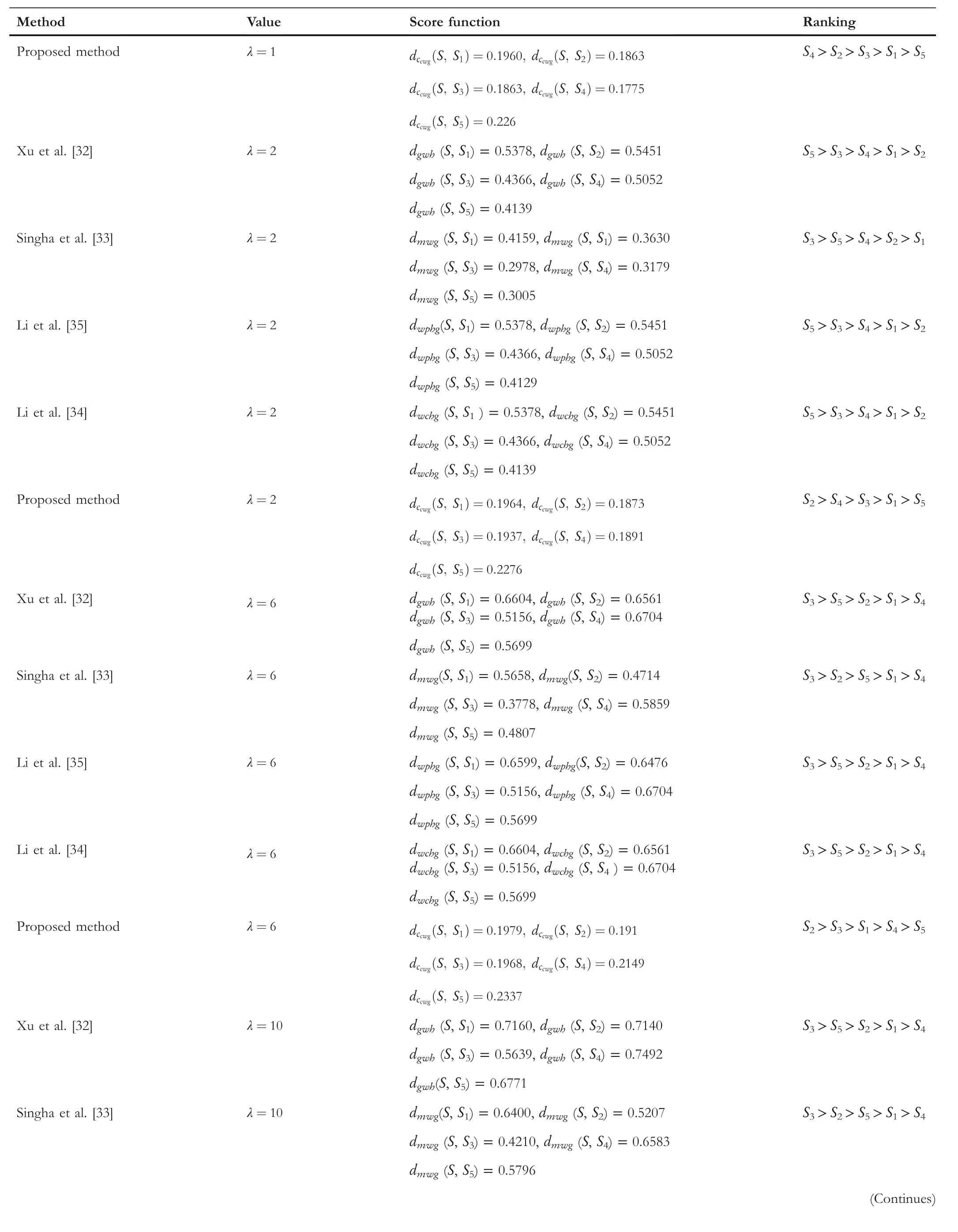
TA B L E 9 (Continued)

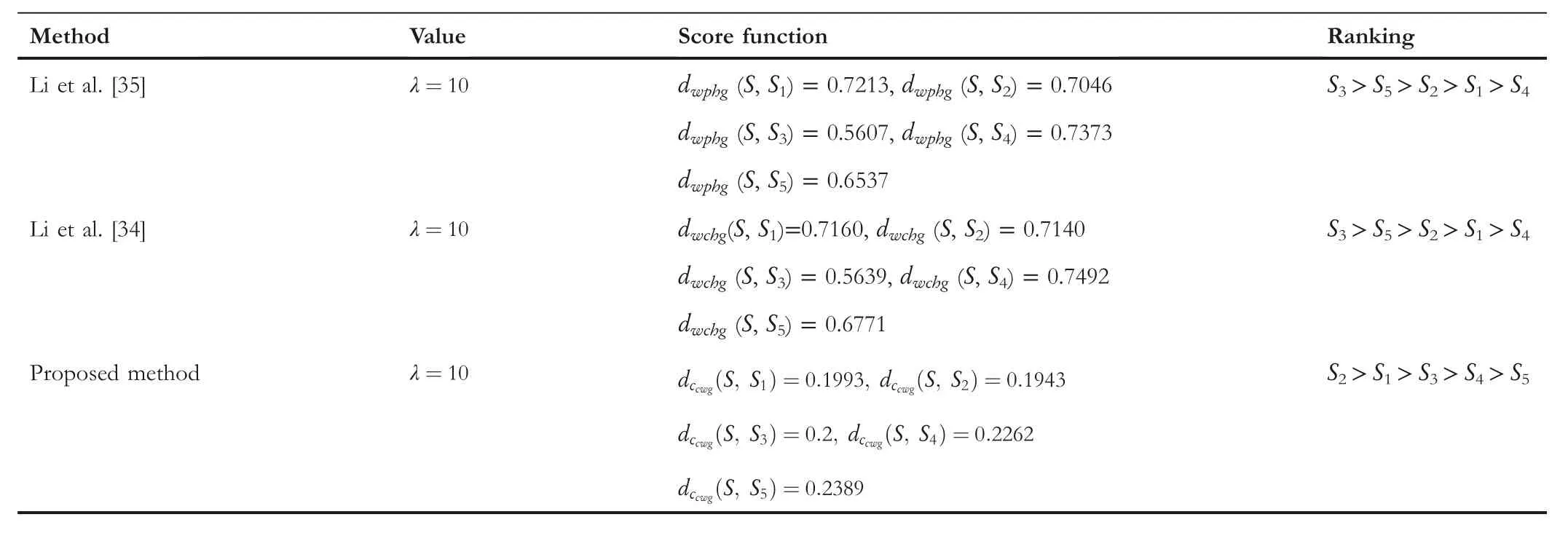
TA B L E 9 (Continued)

TABLE 10 Comparison between the proposed method and existing methods for Example 3 with parameter(αcc,βcc)=(0.9,0.1)

TA B L E 1 0 (Continued)

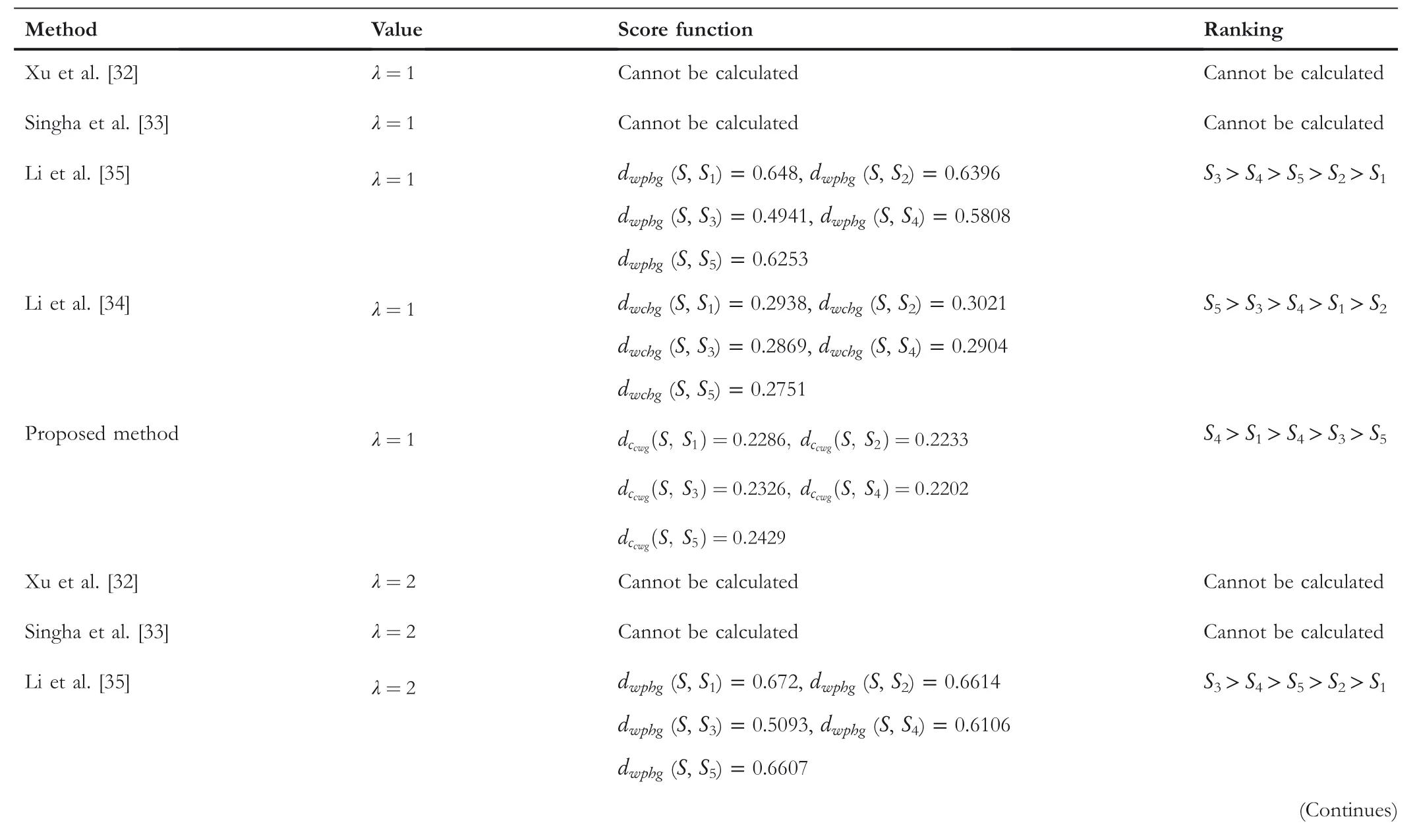
TABLE 11 Comparison between the proposed method and the existing methods for Example 3 with parameter（αcc,βcc）=(0.7,0.3)

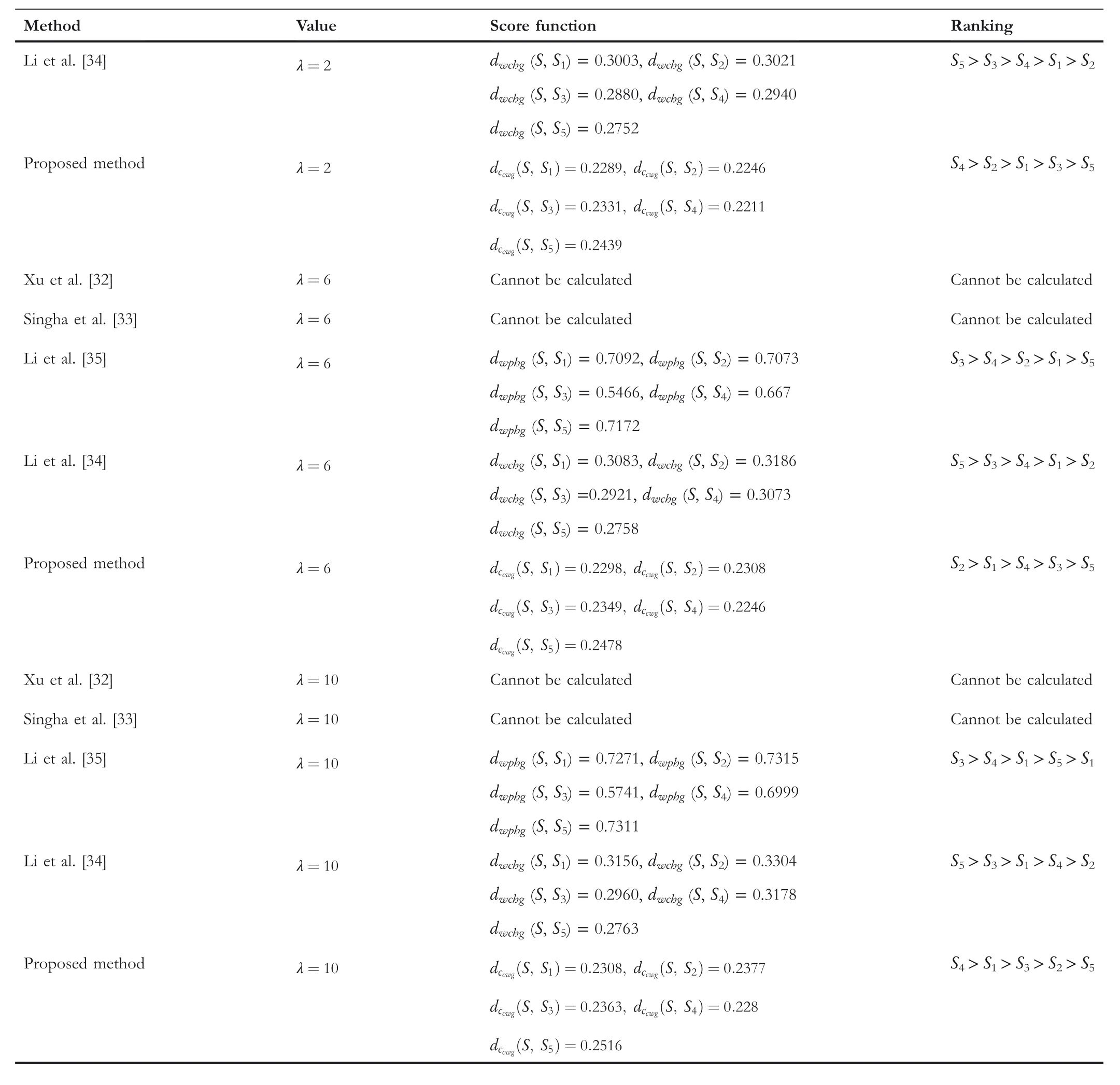
TA B L E 1 1 (Continued)

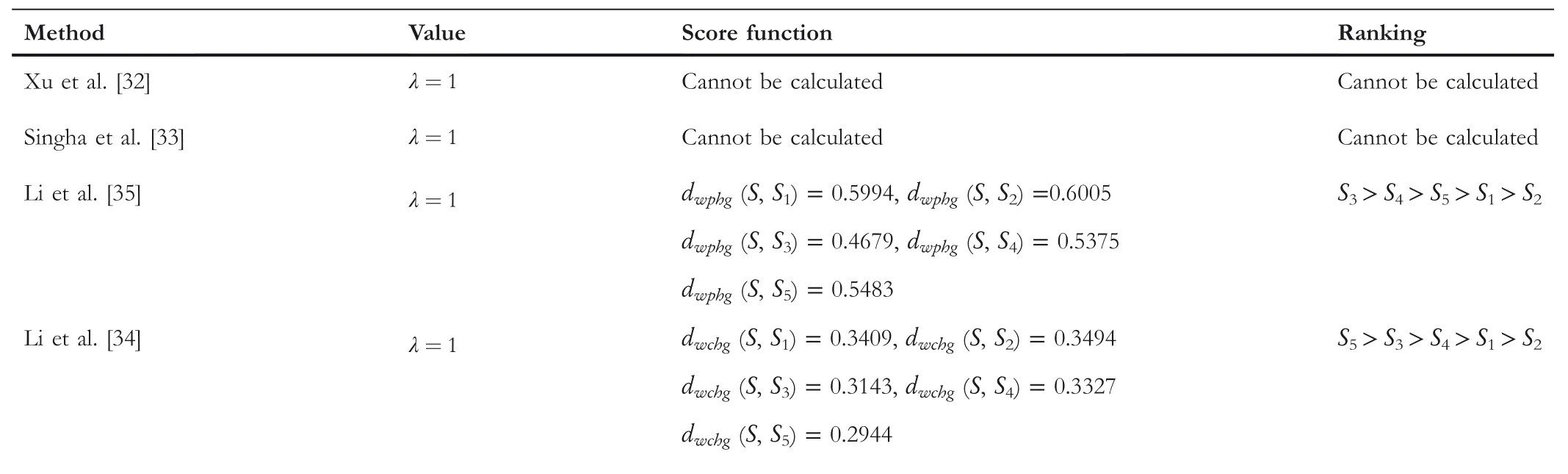
TABLE 12 Comparison between theproposed method and the existing methods for Example 3 with parameter（αcc,βcc）=(0.5,0.5)

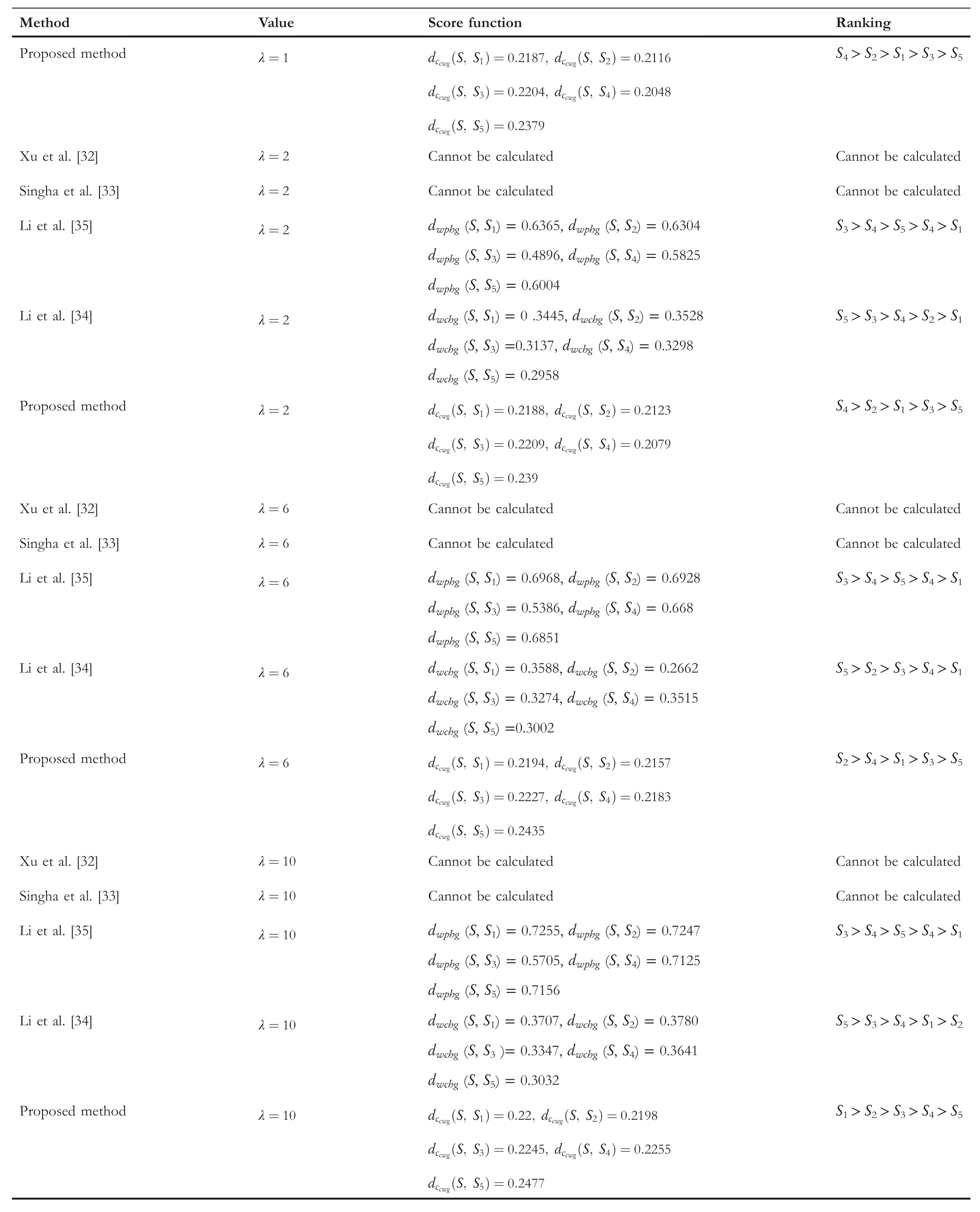
TA B L E 1 2 (Continued)

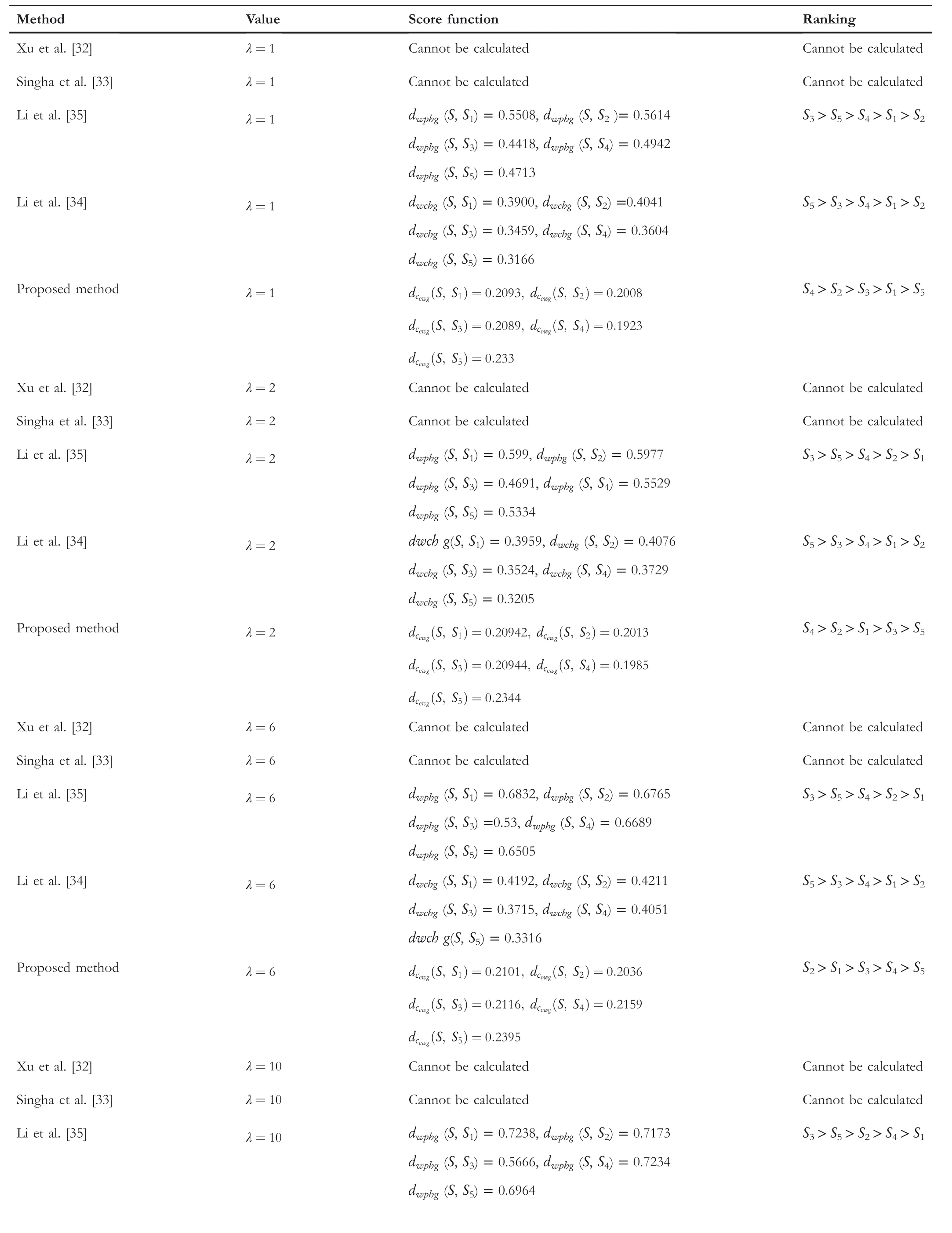
TABLE 13 Comparison between the proposed method and the existing methods for Example 3 with parameter（αcc,βcc）=(0.3,0.7)

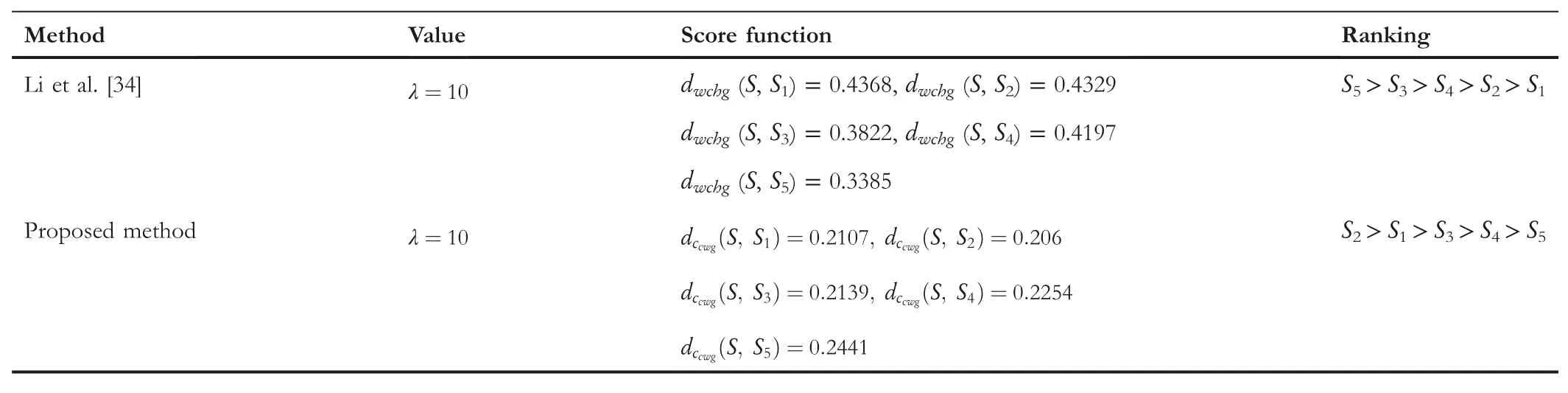
TA B L E 1 3 (Continued)

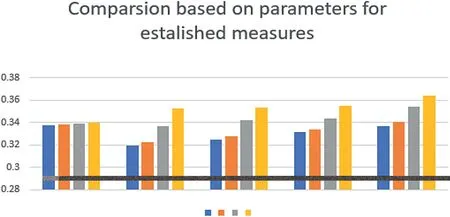
FI GURE 6 Graphical interpretation of the comparison between the established work and the existing work for different values of the parameters

FI GURE 7 Graphical interpretation of the comparison between the established work and the existing work for different values of the parameters

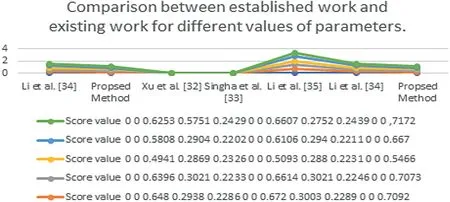
FI GURE 8 Graphical interpretation of the comparison between the established work and the existing work for different values of the parameters

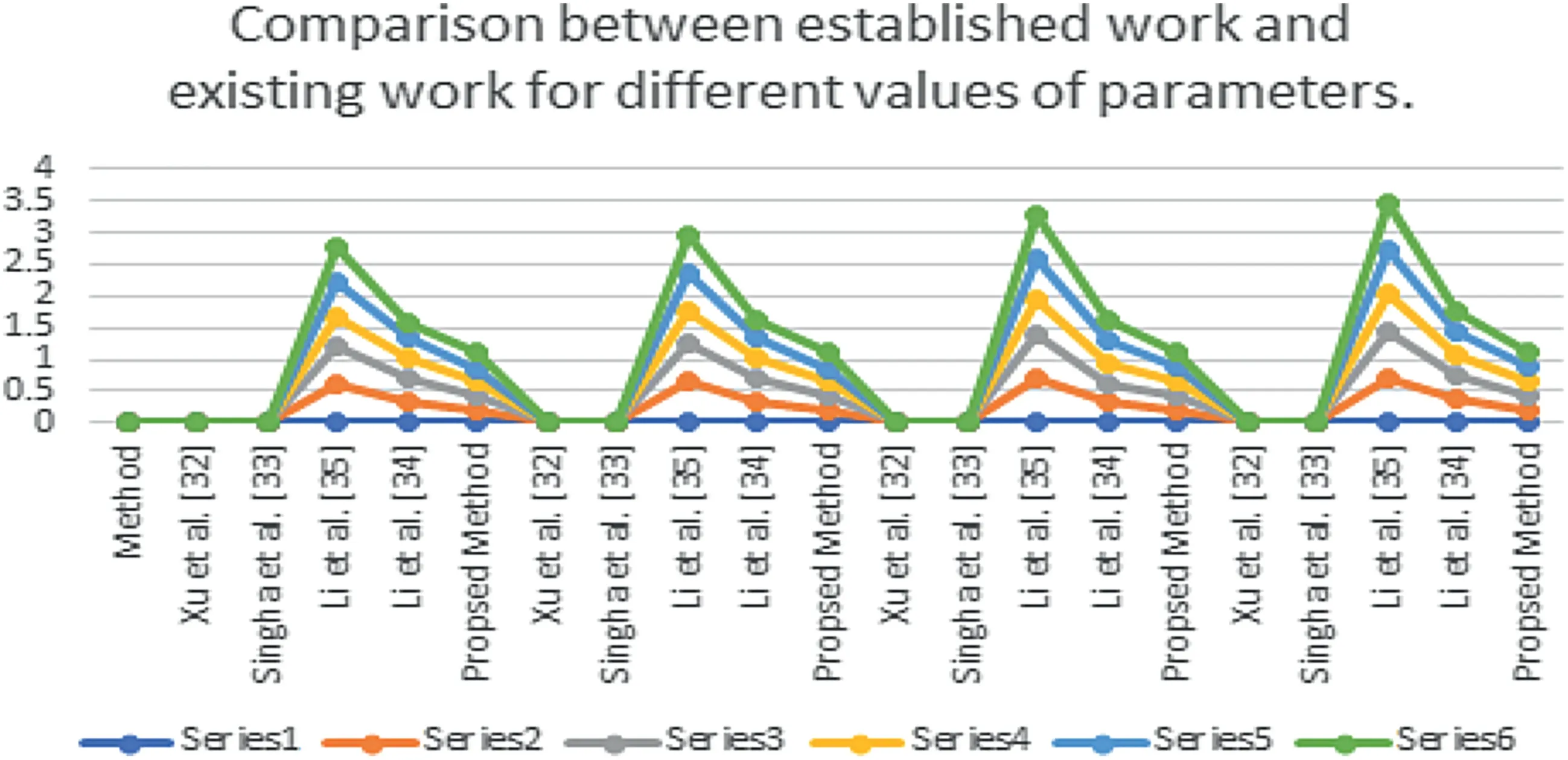
FI GURE 9 Graphical representation of the results

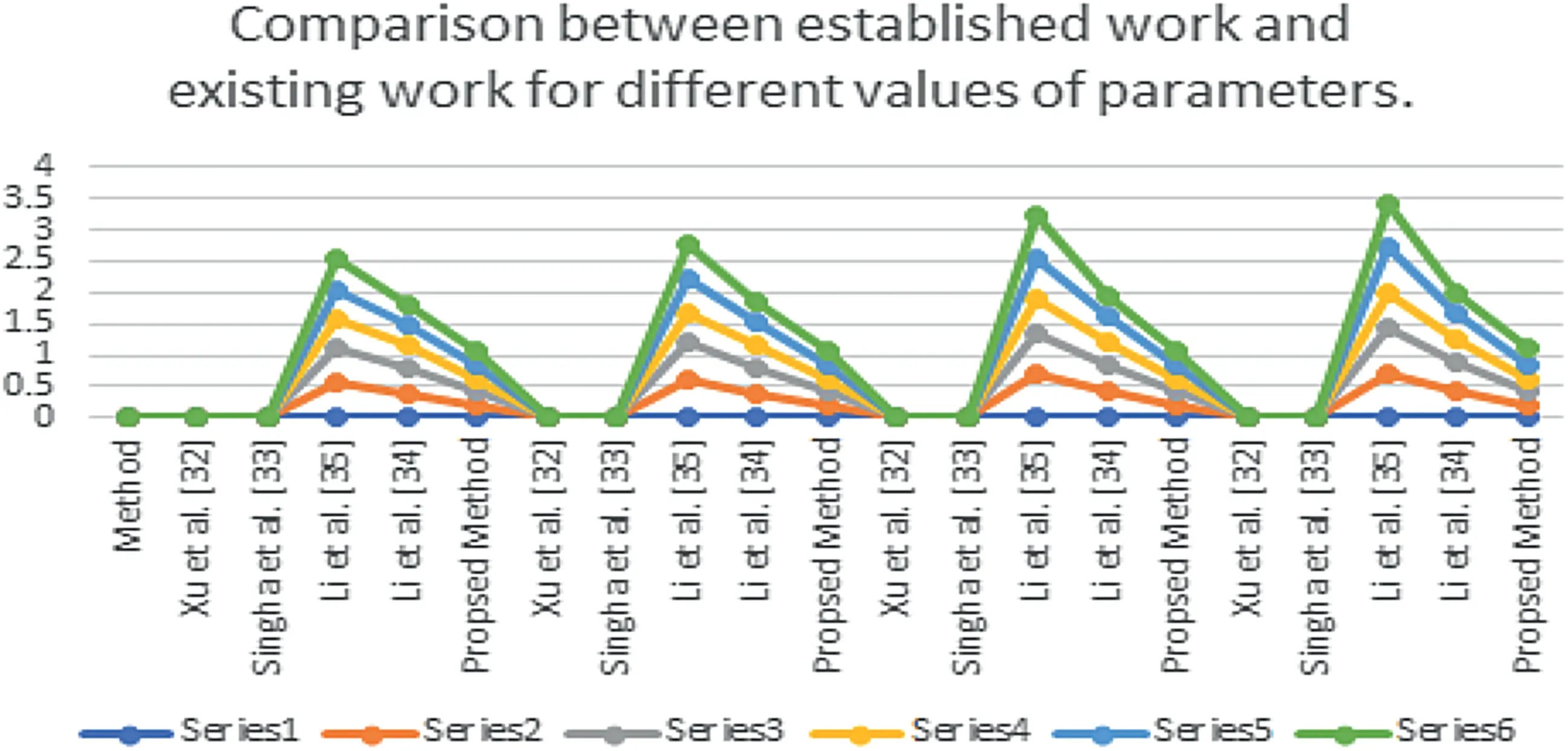
FI GURE 1 0 Graphical interpretation of the comparison between the established work and the existing work for different values of the parameters

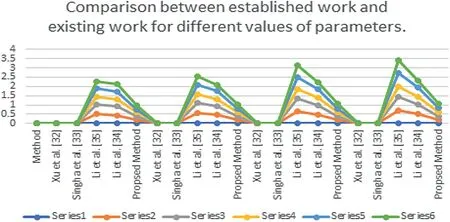
FI GURE 1 1 Graphical interpretation of the comparison between established work and existing work for different values of parameters.Next we show the comparison between the proposed method and the existing methods for Example 2

5.1|Comparison

This section shows the superiority and integrity of the explored work by comparing it with some existing work.

Example3For every society,energy is a crucial factor for socio-economic development.Thus the accurate energy strategy accomplishes economic development and environment,and so,the most suitable energy strategy selection is crucial.Suppose five energy projectsSj(j=1,2,3,4,5)are to be invested.In the meantime,consider four attributes that are given as technological(x1),environmental(x2),socio-political(x3)and economic(x4).Consider the weight for attributes asW=(0.15,0.3,0.2,0.35).After this,a batch of experts is invited to assess the performance of the five alternatives with the respect to four attributes on the notion of excellence.Using HFSs,the assessment results obtained are presented in Table 7.

Suppose an ideal alternative isS*=｛1ei2π（1）｝.Ase0=1 the above data transformed into the CHFSs is shown as follows

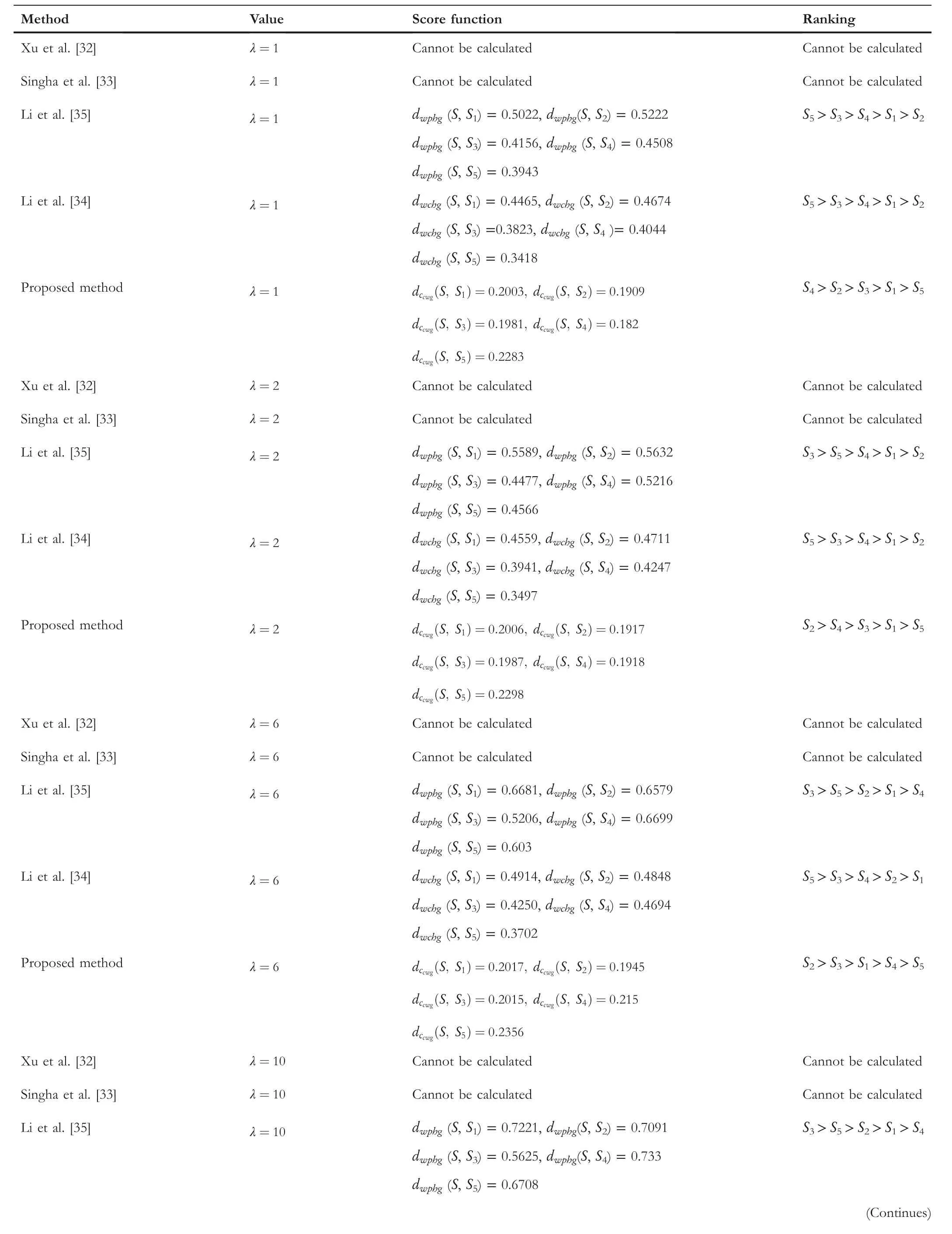
TABLE 14 Comparison between proposed method and existing methods for Example 3 with parameter（αcc,βcc）=(0.1,0.9)

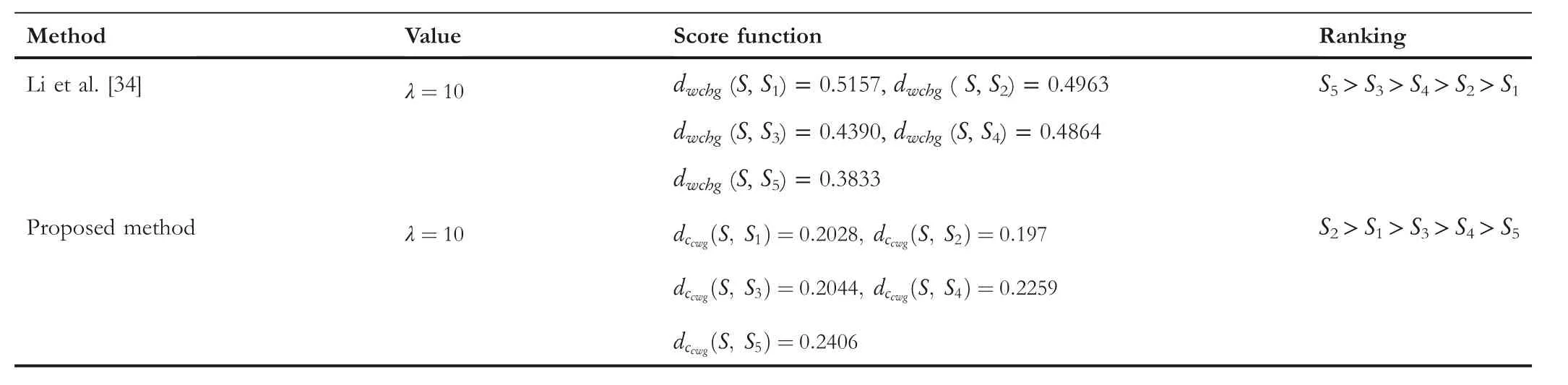
TA B L E 1 4 (Continued)

TAB L E 15 Comparison between the proposed method and existing methods for Example 2 with parameter（αcc,βcc）=(0,1)

TABLE 16 Comparison between the proposed method and the existing methods for Example 2 with parameter（αcc,βcc）=(0.9,0.1)

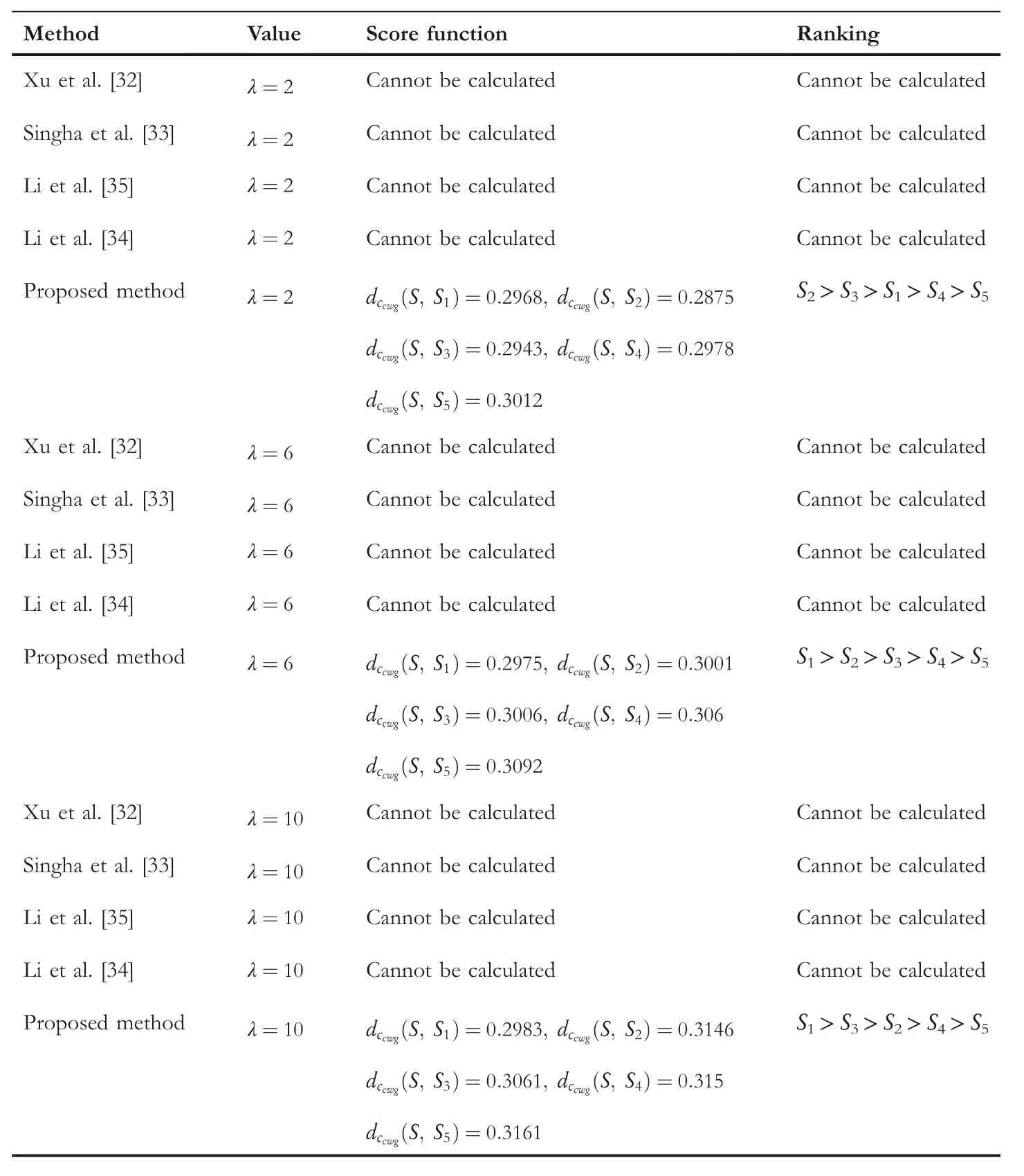
TABLE 17 Comparison between proposed method and existing methods for Example 2 with parameter（αcc,βcc）=(0.7,0.3)

TA B L E 1 7 (Continued )

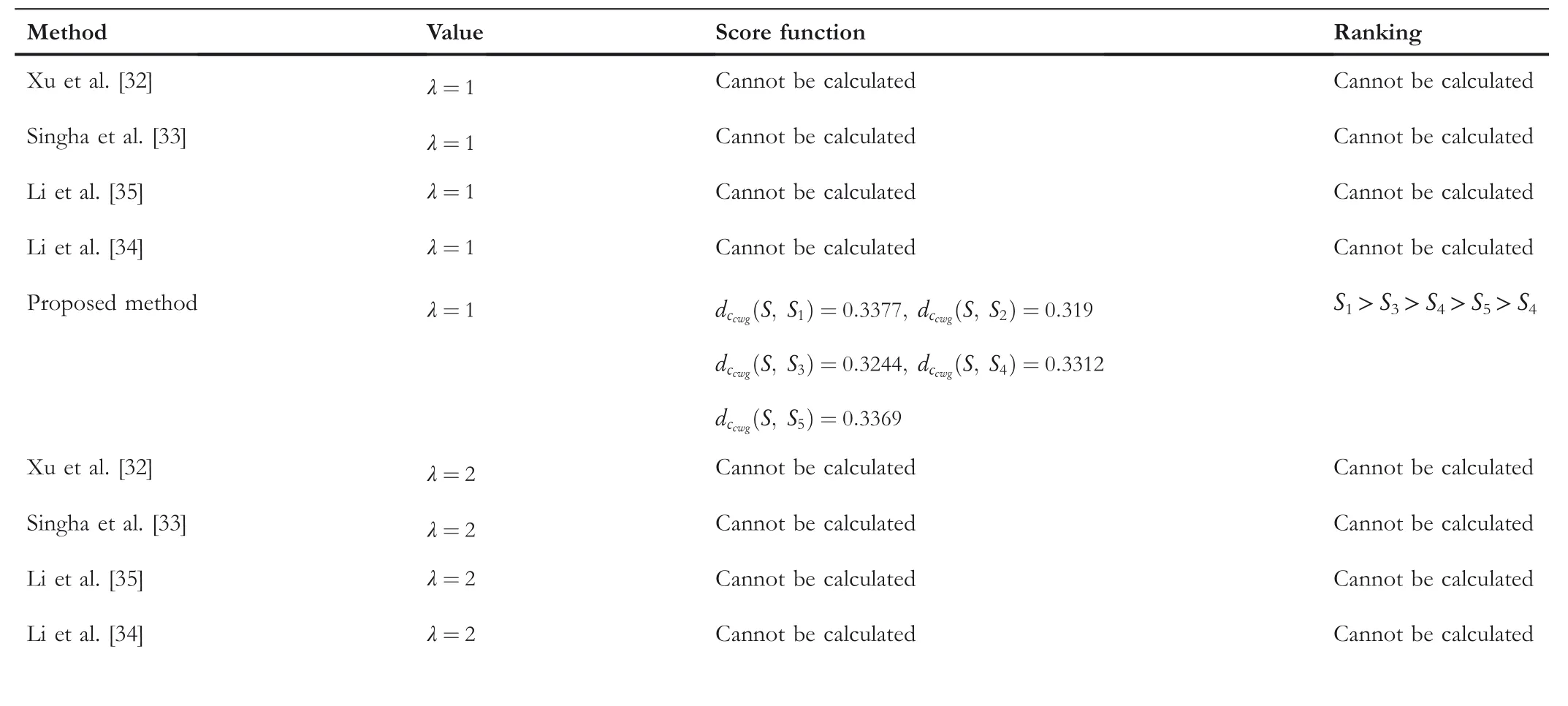
TABLE 18 Comparison between proposed method and existing methods for Example 2 with parameter（αcc,βcc）=(0.5,0.5)

TA B L E 1 8 (Continued)

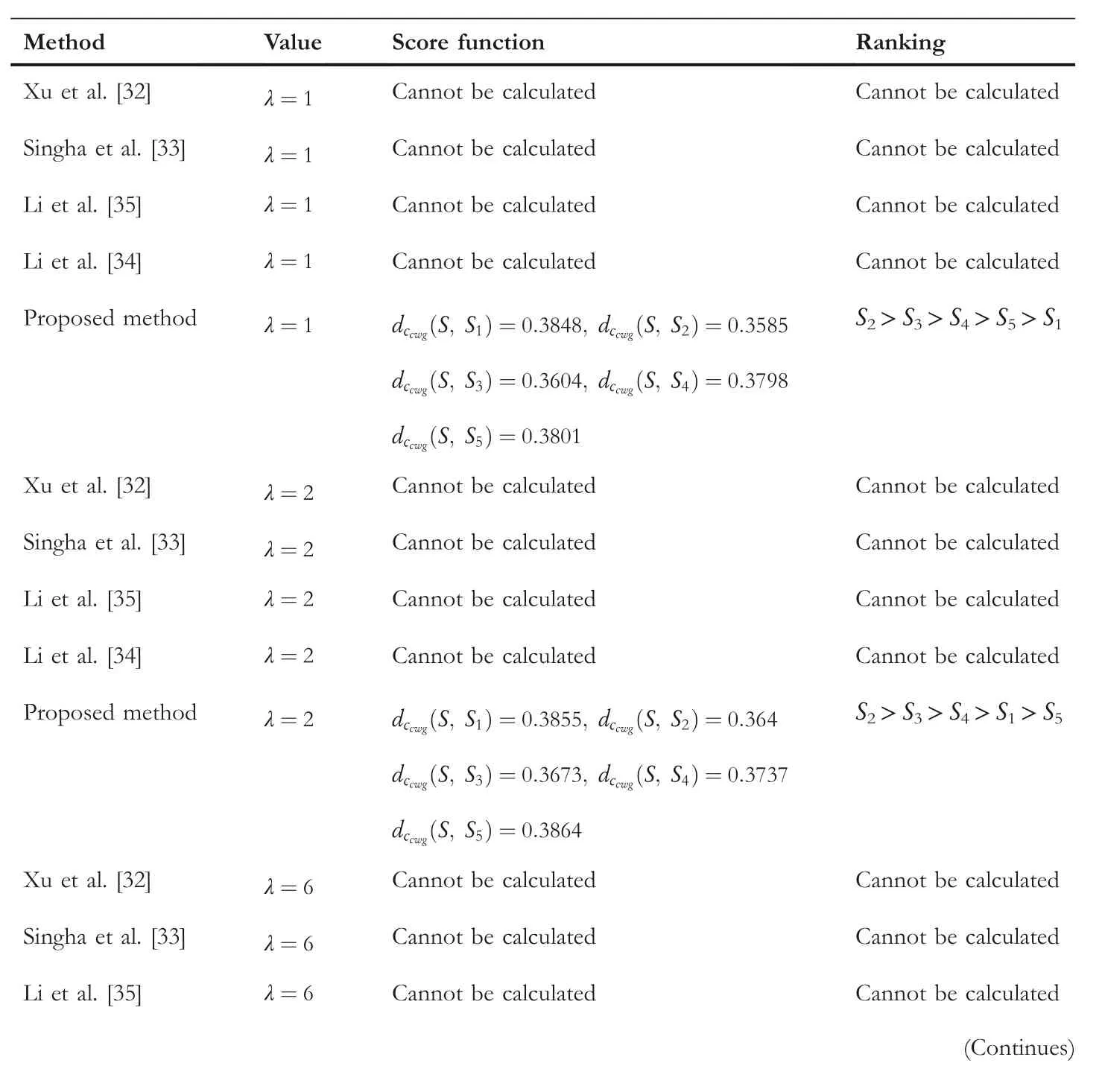
TABLE 19 Comparison between the proposed method and the existing methods for Example 2 with parameter（αcc,βcc）=(0.3,0.7)

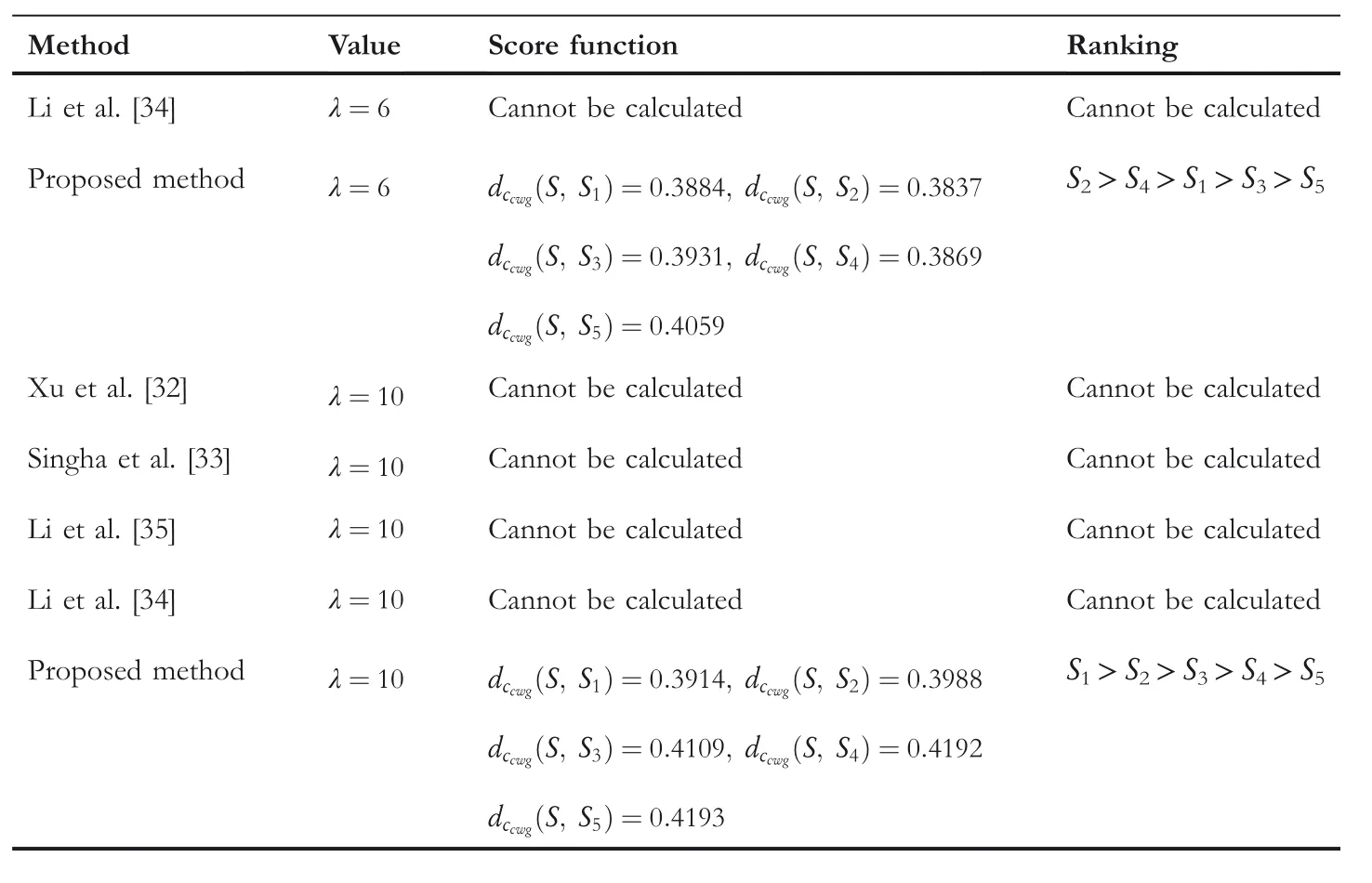
TA B L E 1 9 (Continued)

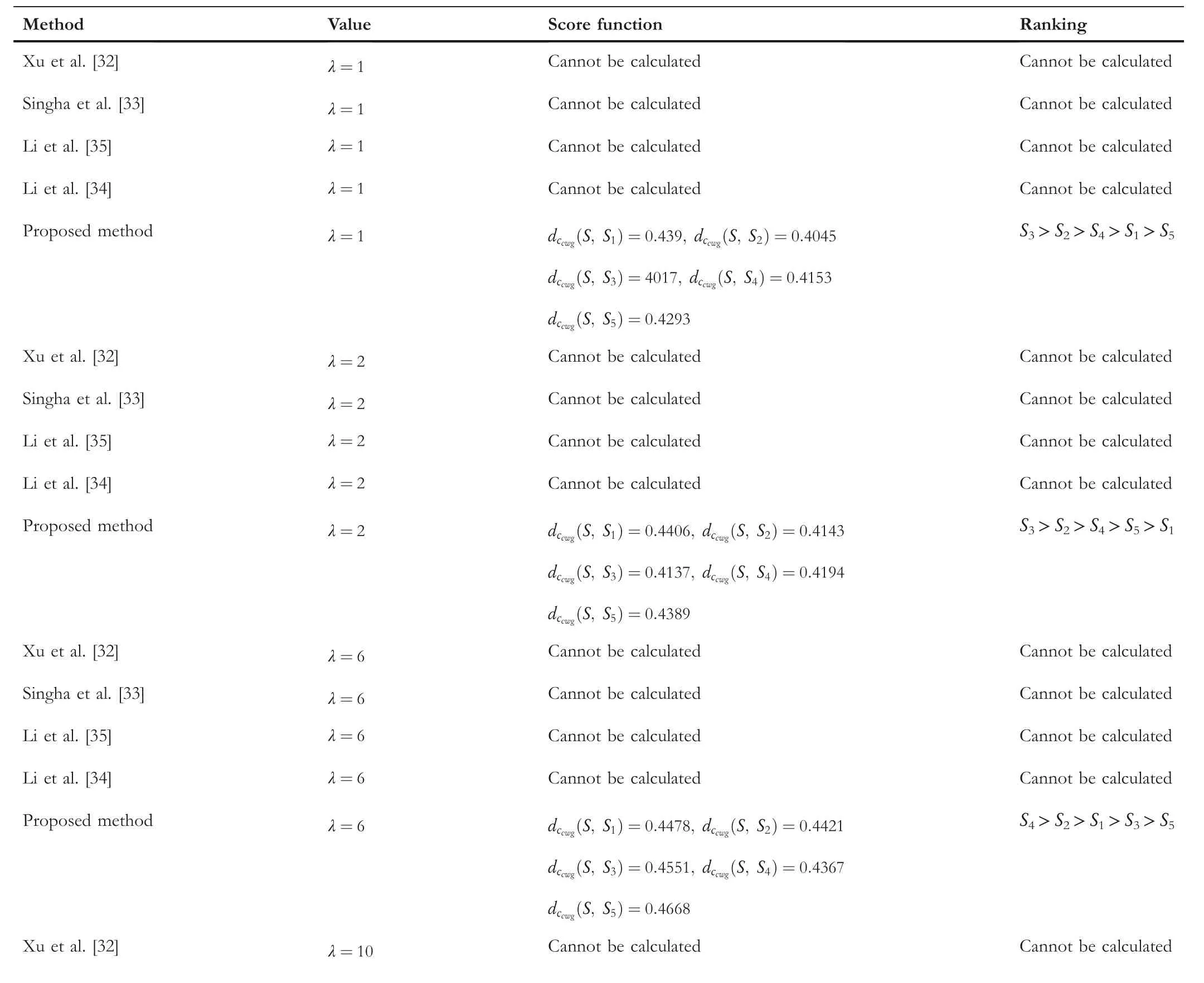
TABLE 20 Comparison between the proposed method and the existing methods for Example 2 with parameter（αcc,βcc）=(0.1,0.9)

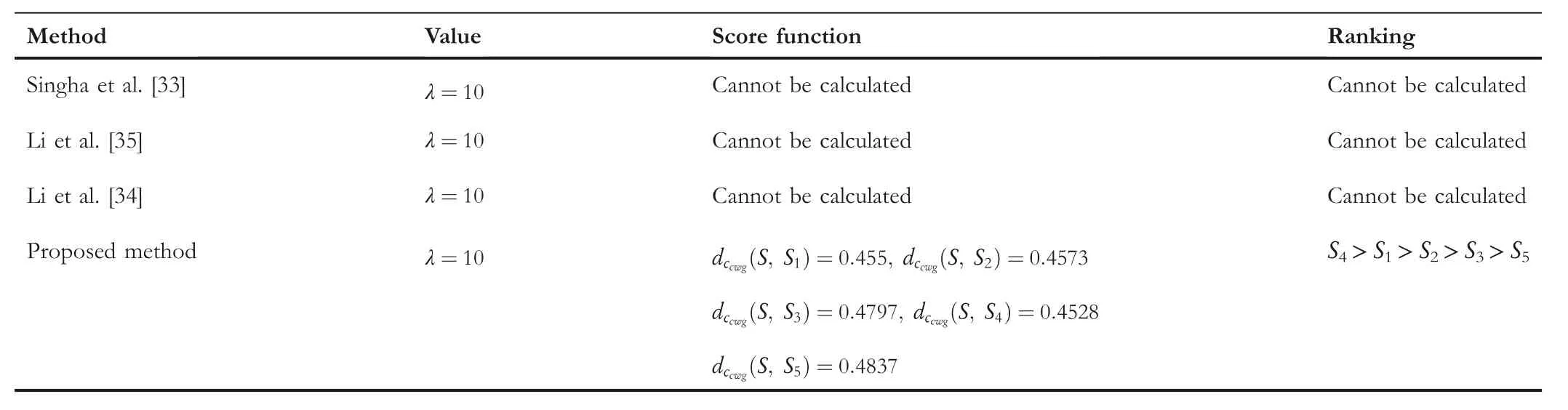
TA B L E 2 0 (Continued)

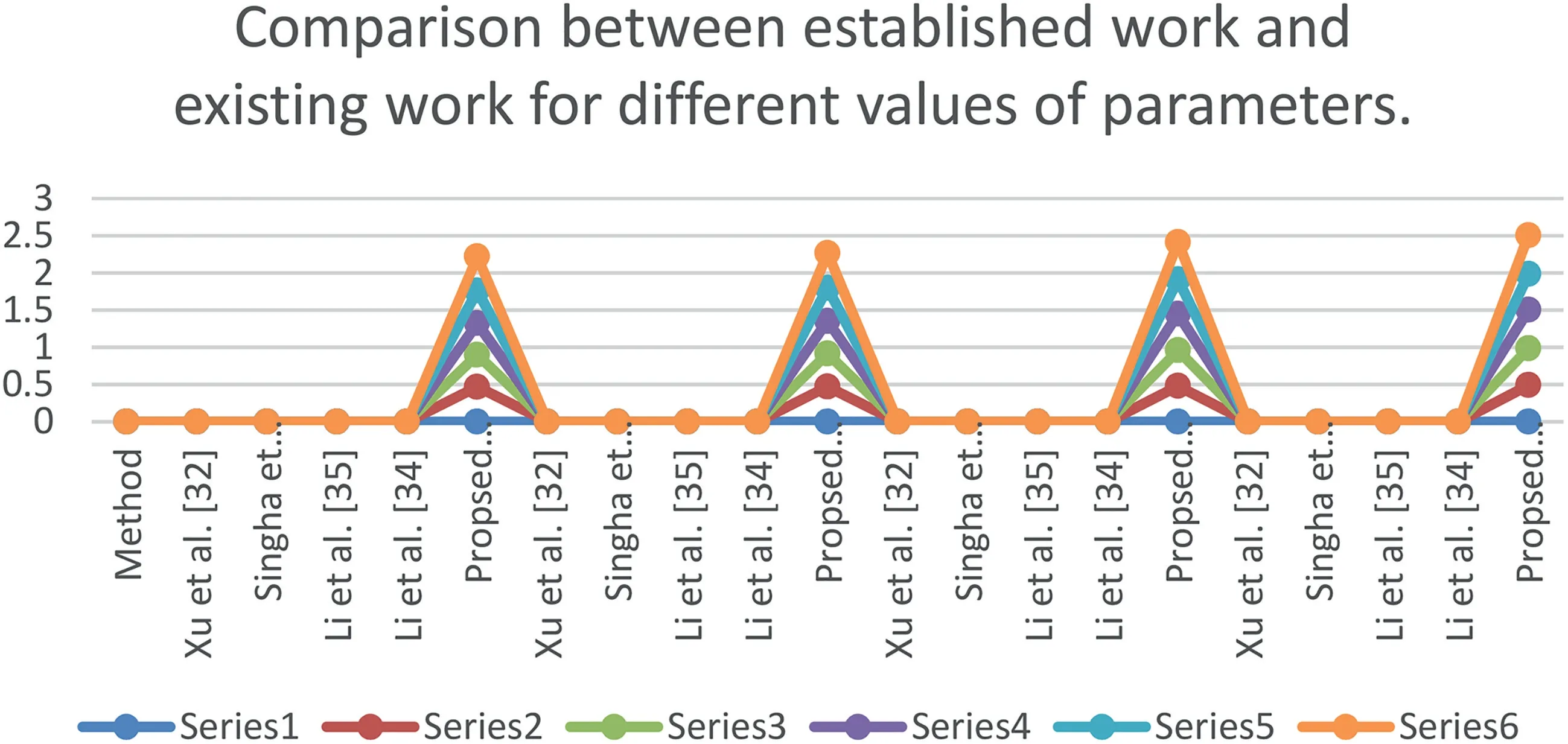
FI GURE 1 2 Graphical interpretation of the comparison between the established work and the existing work for different values of parameters

FI GURE 1 3 Graphical interpretation of the comparison between established work and existing work for different values of parameters

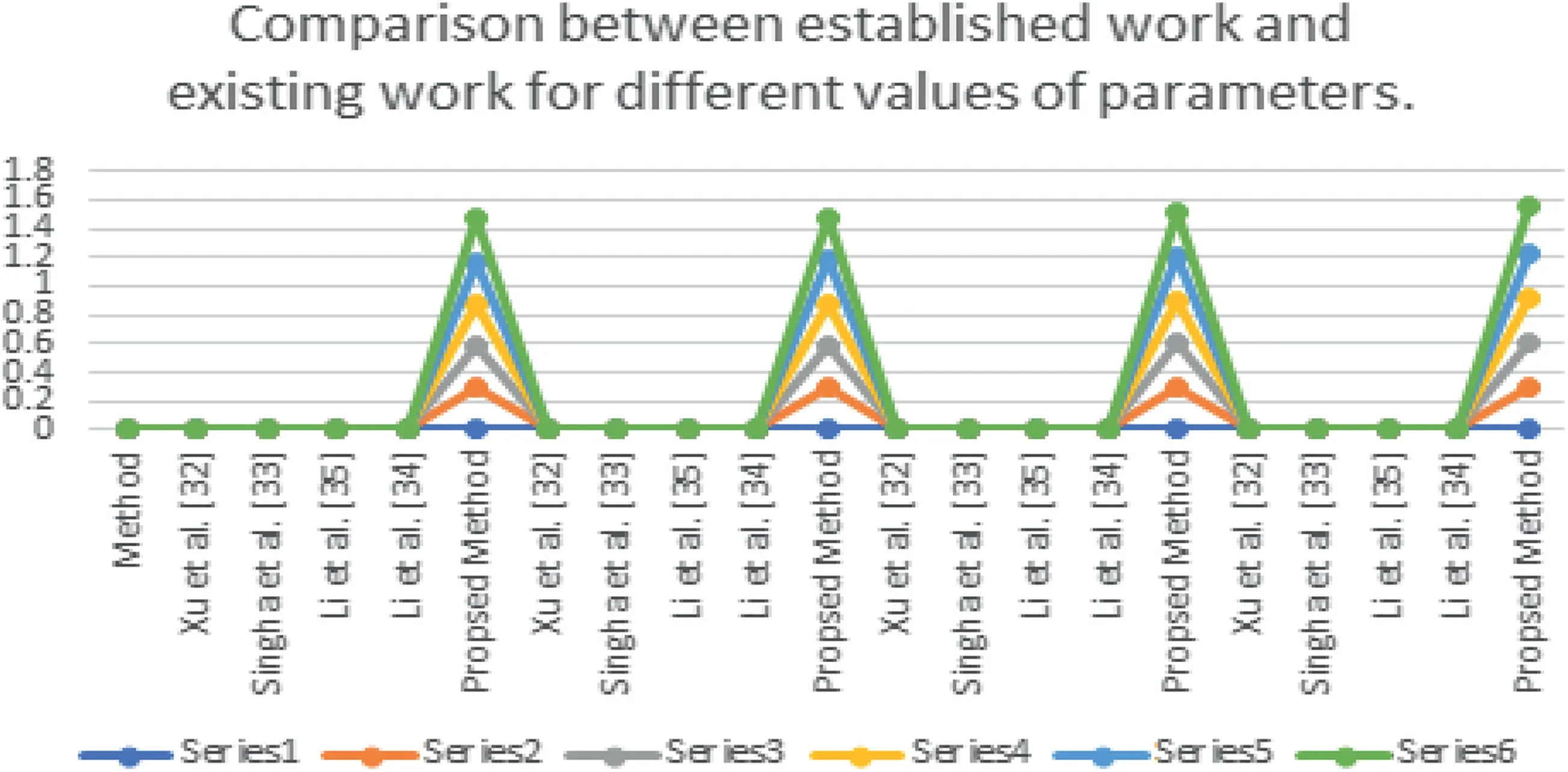
FI GURE 1 4 Graphical interpretation of the comparison between established work and existing work for different values of parameters

F I GURE 1 5 Graphicalinterpretation of the comparison between the established work and the existing work for different values of the parameters

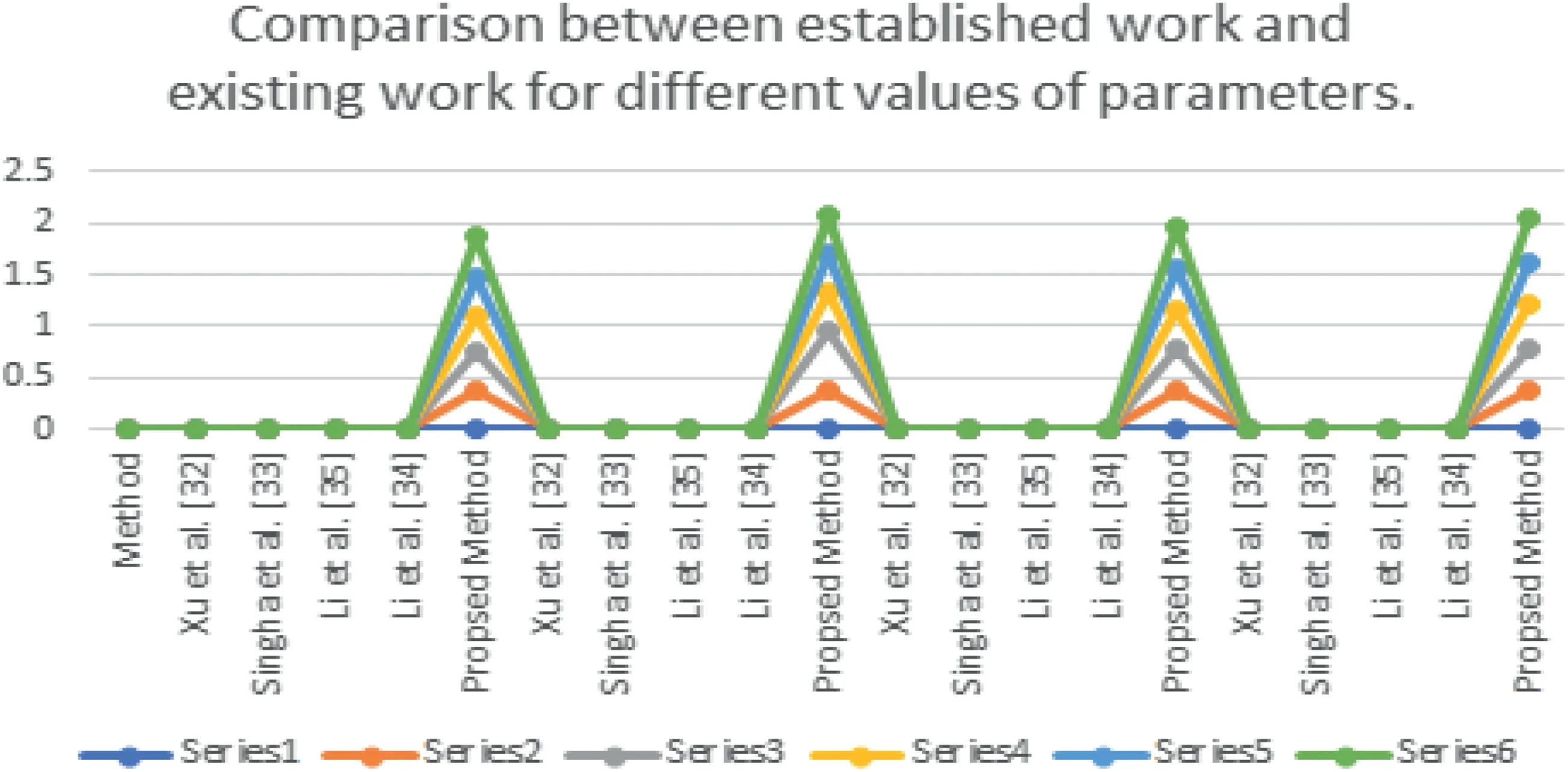
F I GURE 1 6 Graphicalinterpretation of the comparison between established work and existing work for different values of parameters

F I GURE 1 7 Graphicalinterpretation of the comparison between the established work and the existing work for different values of the parameters

The comparison outcomes between the proposed distance measures and existing distance measures for Example 3 are given in Tables 8–13.We observe that the data of Example 3 is in the form HFSs and through the existing distance measures for HFSs,the distance betweenSandSj(j=1,2,3,4,5)is found.Ase0=1,then the given data for Example 3 is transformed to the CHFSs and by the proposed method we find the similarity betweenSandSj(j=1,2,3,4,5)as shown in Tables 8–14.The graphicalrepresentation of such results are shown in Figures 6–11.The comparison outcomes for Example 2 are given in Tables 14–20 and their graphical representation is shown in Figures 12–17.We noted that the data of Example 2 is in the form of CHFSs and the existing methods are incapable achieving this type of data.Through the existing methods,we solve the data in the form of FS,CFS,and HFS.

If we assume the imaginary part as zero,then the explored distance measures are reduced for the HFS.Likewise,if we assume the CHFS as a singleton set then the explored methods are reduced for CFS.Furthermore,if we assume the CHFS as the singleton set and the imaginary part as zero,then the explored methods are reduced for FS.This type of structure makes the explored methods proficient and more general than the existing methods.

6|CONCLUSION

Similarity and distance measures are used to examine the difference between two objects.The objective of the authors is to establish the CHFS,which is the combination of the HFS and CFS to manage complex and awkward information in real-decision theory.Furthermore,the GDMs and MGDMs based on established approaches are utilized and also expose the special cases of the established approach.After this,we established the parameterized distance measures and their particular cases are discussed.The established measures are utilized in the environment of decision-making to examine the feasibility and validity of the explored measures.Moreover,the numerical examples for established measures are solved to express the superiority and integrity/reliability of the explored work.Finally,to evaluate the credibility of the modified and parameterized distance measures based on CHFS,they are verified by comparing with some existing measures.Our future work is to explore the application of CHFNs in many other applications and under different environments[36–42].

ORCID

HarishGarghttps://orcid.org/0000-0001-9099-8422

TahirMahmoodhttps://orcid.org/0000-0002-3871-3845