一类含参半正二阶离散周期边值问题正解的存在性
王 瑞, 路艳琼
(西北师范大学 数学与统计学院, 兰州 730070)
0 引 言
微分方程或差分方程边值问题在计算机科学、 物理学、 经济学、 生态学、 动力系统、 机械系统及交通系统等领域应用广泛. 目前, 边值问题正解的研究已由非线性项正定的条件逐渐拓展到非线性项具有负下界的情形, 这类问题称为半正问题. Castro等[1]在考察二阶微分方程Dirichlet边值问题

(1)
非负解的存在性时, 提出了半正假设:f(0)<0.Anuradha等[2]用锥上不动点定理考察了二阶微分方程

(2)
正解的存在性, 其中λ>0为参数,f: [r,R]×[0,∞)→连续, 且存在常数M>0, 使得f(t,u)≥-M,t∈[r,R],u≥0.Webb等[3]在半正情形下建立了任意阶微分方程
u(n)(t)=λf(t,u(t)),λ>0
(3)
多个正解的存在性.Zhu等[4]基于Leray-Schauder非线性抉择和Guo-Krasnoselskii不动点定理研究了含参半正二阶微分方程周期边值问题

(4)
正周期解的存在性和多解性, 其中λ>0是参数,f: [0,2π]×[0,∞)→满足Carathédory条件. 金立芸等[5]用Guo-Krasnoselskii不动点定理讨论了二阶差分方程m-点特征值问题
(5)
至少一个正解的存在性, 其中f: [0,∞)→连续, 且存在常数M>0使得f(y)≥-M,t∈[a+1,b],λ>0为参数,α,β,ν,δ∈[0,∞),ci,di∈[0,∞),i∈{1,2,…,m-2}.李建平等[6]利用锥拉伸与锥压缩不动点定理在非线性项具有负下界和非减性条件下, 讨论了二阶半正定非线性差分方程

(6)
正解的存在性, 其中T>1是一个给定的正整数.
离散周期边值问题是一类重要的差分问题, 在非线性项f非负的情形下关于其解的存在性与多解性研究已有很多结果[7-10].王晶晶等[8]在非线性项f非负时给出了

(7)
正解的存在性结果, 其中a: [1,N]→(0,∞), 且但目前关于半正离散周期边值问题正解的存在性研究尚未见文献报道, 基于此, 本文研究半正二阶离散变系数周期边值问题

(8)
其中λ>0, [1,T]={1,2,…,T},a: [1,T]→(0,∞)且连续, 且满足如下假设:
(H1) 存在常数D>0, 使得f(t,u)≥-D, (t,u)∈[1,T]×[0,∞);

(H3) 存在两个常数b,d∈(0,∞), 使得0 令[a,b]={a,a+1,…,b}, 设u(t)是定义在[a,b]上的函数, 则Δu(t)=u(t+1)-u(t)称为u(t)在t点的一阶差分, Δ称为(前向)差分算子, 记I为恒等算子, 即Iu(t)=u(t).当n2 E∶={u|u: [0,T+1]→,u(0)=u(T), Δu(0)=Δu(T)}, 由文献[11]中推论2.5可知, 问题(8)对应的齐次问题 (9) 是非共轭问题, 只有平凡解且格林函数G(t,s)>0, (t,s)∈[1,T]×[1,T]. 设φ和ψ分别是初值问题 的唯一解, 则: 1)φ(t)≥0且Δφ(t)≥0,t∈[1,T]; 2)ψ(t)≥0且Δψ(t)≤0,t∈[1,T]. 引理1[11]设a: [1,T]→(0,∞)且则问题(9)的格林函数为 (10) 引理2设u满足边值问题 (11) 其中v: [1,T]→且v≥0, 则 证明: 设存在t0∈[1,T], 使得‖u‖=u(t0), 则对∀t∈[1,T], 有 (12) 证明: 对∀t∈[1,T], 1) ‖Au‖≤‖u‖, ∀u∈K∩∂Ω1; ‖Au‖≥‖u‖, ∀u∈K∩∂Ω2; 2) ‖Au‖≥‖u‖, ∀u∈K∩∂Ω1; ‖Au‖≤‖u‖, ∀u∈K∩∂Ω2. (13) (14) (15) 的解, 则 由引理2可知, 对∀u∈K, 即AK⊂K, 且因为E是有限维空间, 故易证A:K→K是全连续的. 定义Ω1={u∈E|‖u‖<1}.设u∈K∩∂Ω1, 则 即∀u∈K∩∂Ω1, ‖Au‖≤‖u‖. 从而 故 且 于是 即∀u∈K∩∂Ω2, ‖Au‖≥‖u‖. 则问题(8)至少存在两个正解, 其中C2=max{|f(t,u)||t∈[1,T], 0≤u≤L}. 证明: 由定理1的证明可知, 问题(8)存在第一个正解u1满足‖u1‖>m/(2M).下面证明存在第二个正解.记 (16) 则0 考虑问题(8)的辅助问题: (17) 定义Ω3={u∈E|‖u‖ 即∀u∈K∩∂Ω3, ‖Fu‖≤‖u‖. 定义Ω4={u∈E|‖u‖ 其中t*∈[1,T]为任意一点.因此∀u∈K∩∂Ω4, ‖Fu‖≥‖u‖. 注2文献[8]建立了非线性项f≥0且格林函数G(t,s)≥0时问题(7)正解的存在性结果, 本文在G(t,s)>0时将非线性项f推广到半正情形, 得到了问题(8)正解的存在性与多解性结果. 例1考虑二阶离散周期边值问题: (18) 容易验证对∀t∈[1,10]和u∈[0,∞), 有即存在一个常数使得假设(H1)成立;对∀t∈[1,10]一致成立, 即假设(H2)成立; 存在正常数使得即假设(H3)成立.因此由定理1可知, 当时, 问题(18)至少存在一个正解; 由定理2可知, 当 时, 问题(18)至少存在两个正解.
1 预备知识
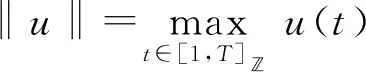
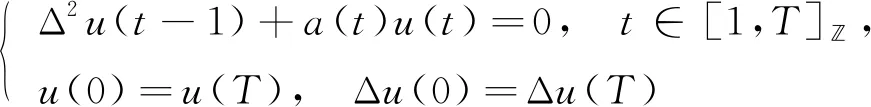







2 主要结果