修正Broer-Kaup-Kupershmidt (mBKK)方程组的李对称分析,非线性自伴随及守恒律

史婷婷, 张顺利

(西北大学数学学院, 陕西 西安 710127)

1 引言

对称和守恒律在物理, 数学和其他自然科学领域有着举足轻重的作用. 无穷多守恒律的存在是证明方程的可积性的强有力证据, 对于一个具有无穷多自由度的非线性系统, 如果它具有无穷多的对称性和守恒律, 则该系统是在具有无穷多守恒律意义下的可积系统[1-2]. 为了寻求非线性系统的对称和守恒律, Ibragimov 提出了伴随方程法[3-5],该方法可以用来寻求任意微分方程的李对称, Lie-B¨acklund 对称或留数对称有关的守恒律, 并得到了广泛应用[6-11]. 本文首先运用李群分析法求得mBKK 方程组李对称, 并证明该方程组具有非线性自伴随性, 最后结合方程组的非线性自伴随性及求得的李对称, 运用伴随方程法构造mBKK 方程组的守恒律.

对于(2+1) 维Broer-Kaup-Kupershmidt 方程组

当y=x时, 可将其化为(1+1) 维BKK 方程组

将上面的方程组改写为mBKK 方程组

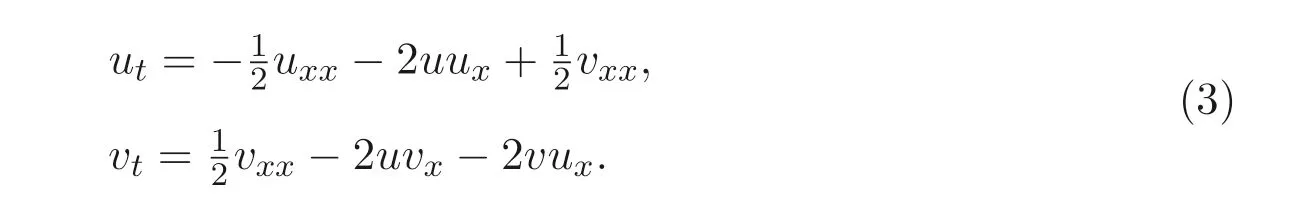
方程组(1) 是描述非线性和色散长重力波在浅海水平方向均匀深度的模型, 它被广泛应用于等离子体物理、液体力学、非线性光学等各个领域. 文献[12] 用Hirota 方法把该方程化为双线性方程, 然后通过摄动法寻找其精确解; 文献[13] 用李群方法得到该方程的对称和相似约化, 并借助辅助函数法求解约化方程, 从而得到其部分精确解; 文献[14] 用修正CK 直接法得到方程的对称、约化, 再通过求解约化方程得到该方程组的一些精确解. 经查找知, 相关文献主要针对(2+1) 维Broer-Kaup-Kupershmidt 方程组进行研究, 而对mBKK 方程研究较少. 文献[15] 用Painlev´e分析法, 证明mBKK 方程具有用Painlev´e 性质, 且在Painlev´e 分析的基础上通过Schwarz 导数的性质, 求出了方程的精确解. 本文则主要研究mBKK 方程的对称、自伴随性及守恒律.

2 mBKK 方程的李对称分析

mBKK 方程组(3) 可写为

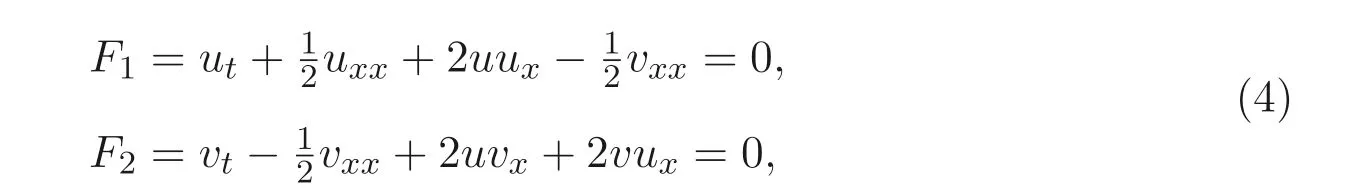
则方程组(4) 的单参数李群的无穷小变换为

这里小参数ϵ ≪1, 则变换群(5) 对应的向量场为:

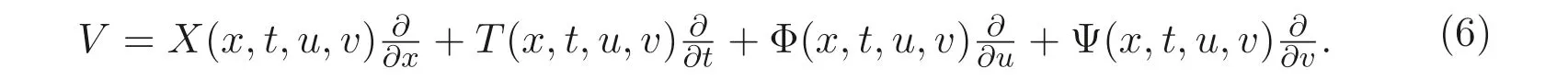
若向量场(6) 是方程组(4) 的李对称, 则要求方程组(4) 在变换u=u+ϵσ1,v=v+ϵσ2下保持形式不变. 这里

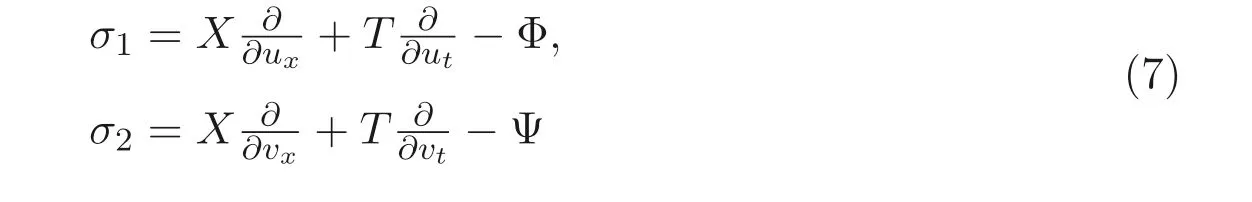
表示u,v的满足方程的对称.σ1,σ2满足方程组(4) 的线性方程组

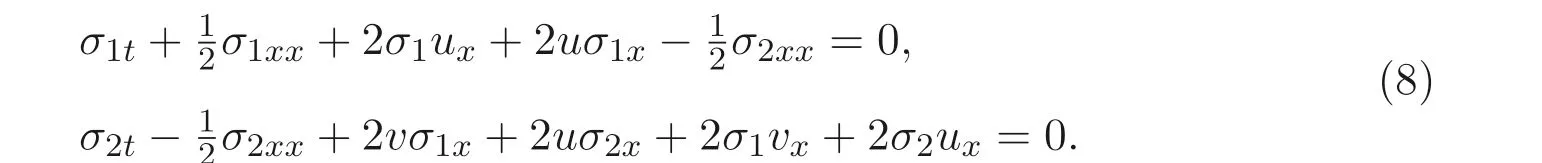
将方程组(7) 带入方程组(8) 中, 由原方程消去ut,vt, 然后再令u,v的各阶导数项系数为零, 即可得到一组关于X,T,Φ,Ψ 的线性方程组, 从而可求得

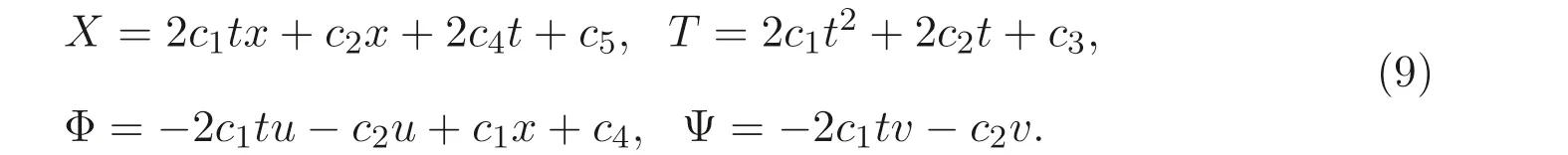
这里c1,c2,c3,c4,c5是任意常数.

基于表达式(9), 由李群分析法可得方程组(4) 的所有向量场

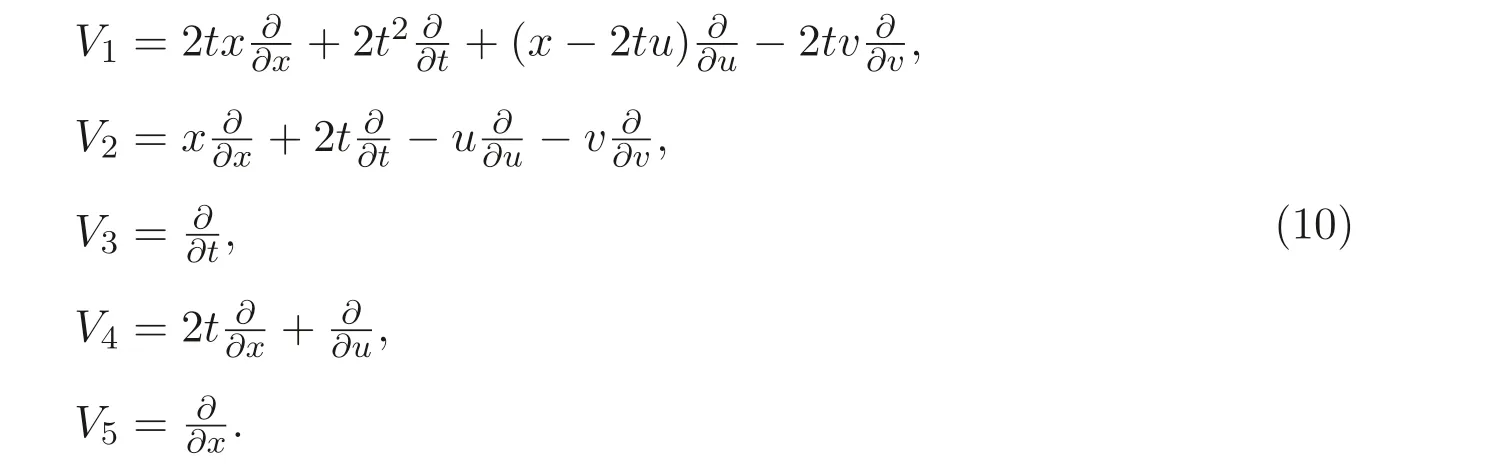
由向量场得方程组(4) 的单参数变换群为

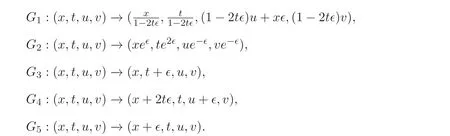
这里ϵ为任意常数. 由于Gi(i=1,2,3,4,5) 为不变群, 故有如下定理. 即

定理2.1[16]如果u=f(x,t),v=g(x,t) 是方程组(4) 的解, 则由Gi确定的方程组(4) 的群不变解为

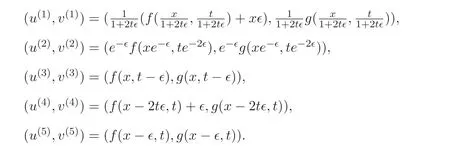
即(u(i),v(i)) 也是方程组(4) 的解.

下面给出向量场(10) 对应的李代数交换子表(见表1).

表1 李代数交换子表

这里[Vi,Vj]=ViVj-VjVi, (i,j=1, 2, 3, 4, 5) 表示的是李代数交换子.

3 mBKK 方程的自伴随性

定义3.1[5]非线性系统

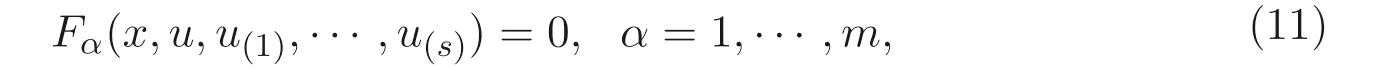
这里x= (x1,··· ,xn),u= (u1,··· ,um),u(s)为u关于自变量的s阶偏导数. 则非线性系统(11) 的伴随系统为

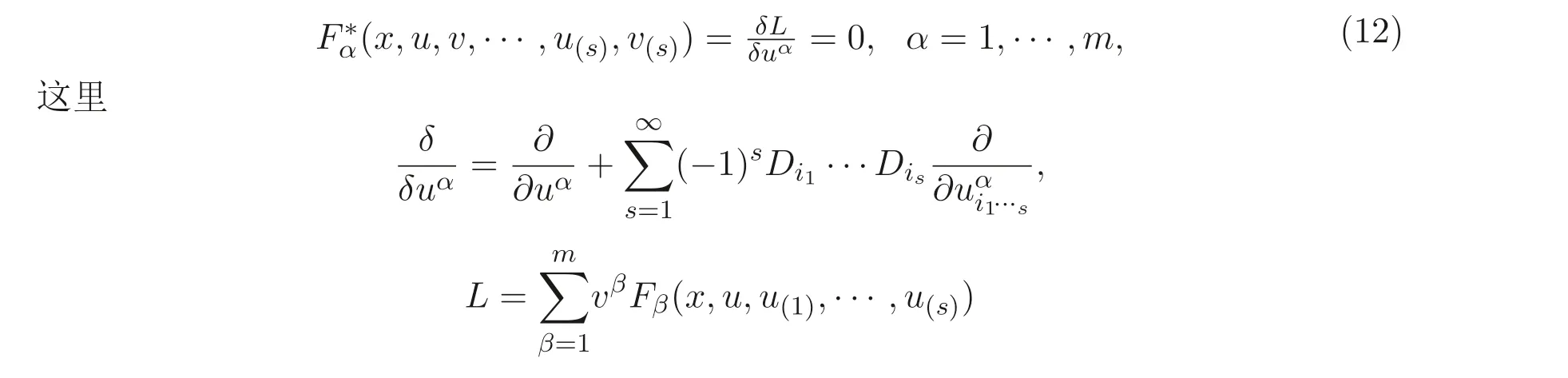
表示的是非线性系统(11) 的标准Lagrangian 函数.

定义3.2[5]非线性系统(11) 具有自伴随性, 如果它的伴随系统(12) 在变换vβ=um下等于非线性系统(11).

定义3.3[5]非线性系统(11) 具有非线性自伴随性, 如果它的伴随系统(12) 满足

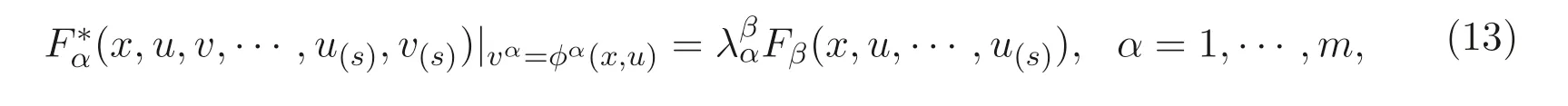
这里u1=u1(x,t),v1=v1(x,t) 为新的因变量.

由定义3.2, 方程组(4) 不具有自伴随性. 又由定义3.3, 如果能找到

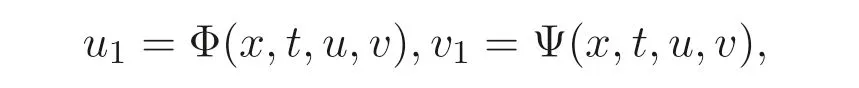
使其满足方程组(13), 且Φ(x,t,u,v),Ψ(x,t,u,v) 不全为零, 则表示方程组(4) 是具有非线性自伴随性的. 换句话说, 方程组(4) 是具有非线性自伴随性的, 如果其伴随方程组满足

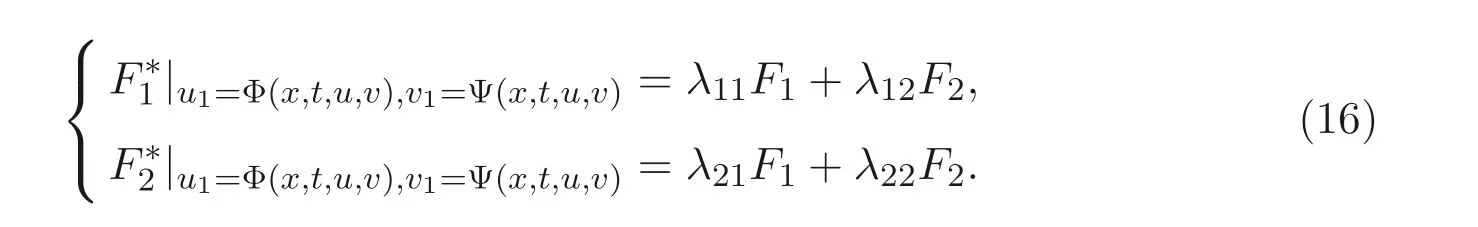
将方程组(4), 方程组(14) 带入方程组(16), 因Φ,Ψ 不依赖于导数ut,vt,uxx,vxx,···,故方程组(16) 关于系数λij(i,j=1,2) 可分解为如下方程组

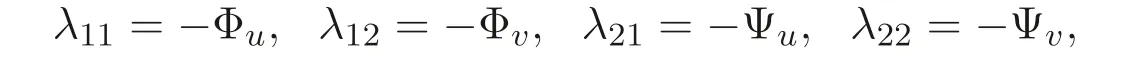
再将上述方程组带入方程组(16) 中, 得超定方程组

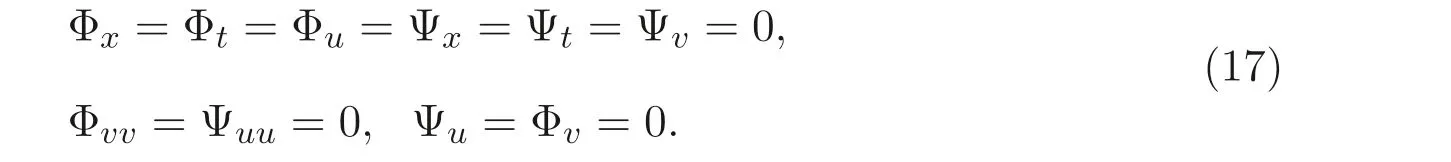
解方程组(17) 可得

这里b1,b2为非零常数. 从而方程组(4) 在变换(18) 下是具有非线性自伴随性的.

4 mBKK 方程组的守恒律

定理4.1[4]方程组(4) 的任意一个李对称, Lie-B¨acklund 对称及留数对称都可以确定方程组(4) 的一个守恒律, 且其守恒向量场C=(C1,C2) 的表示形式为

这里Wα=ηα −ξjuαj.

由定理4.1 的结论, 设向量场的通式为

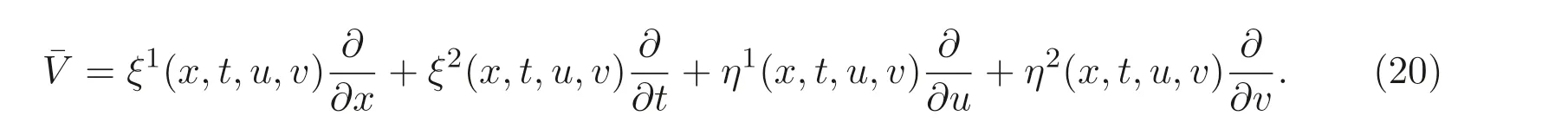
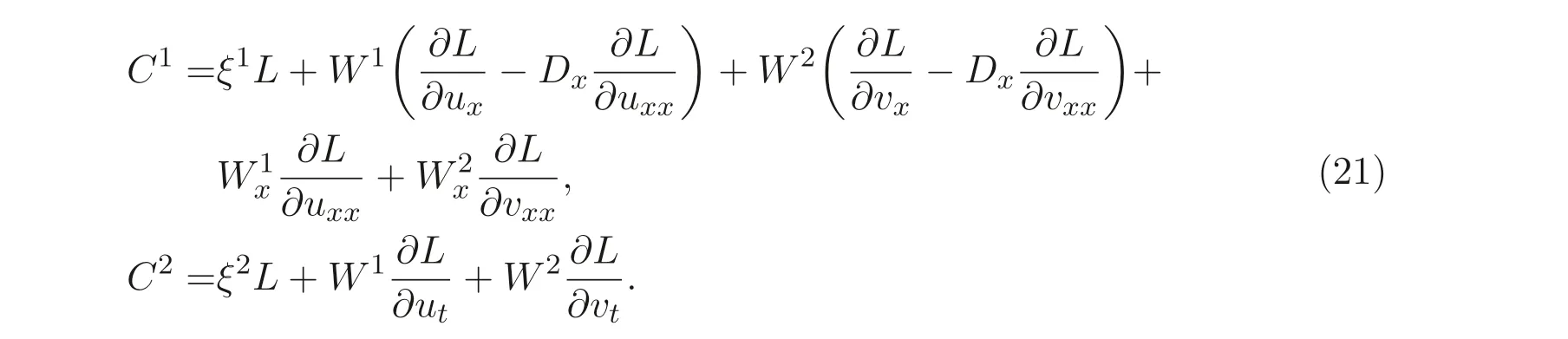
将L带入(21) 式有

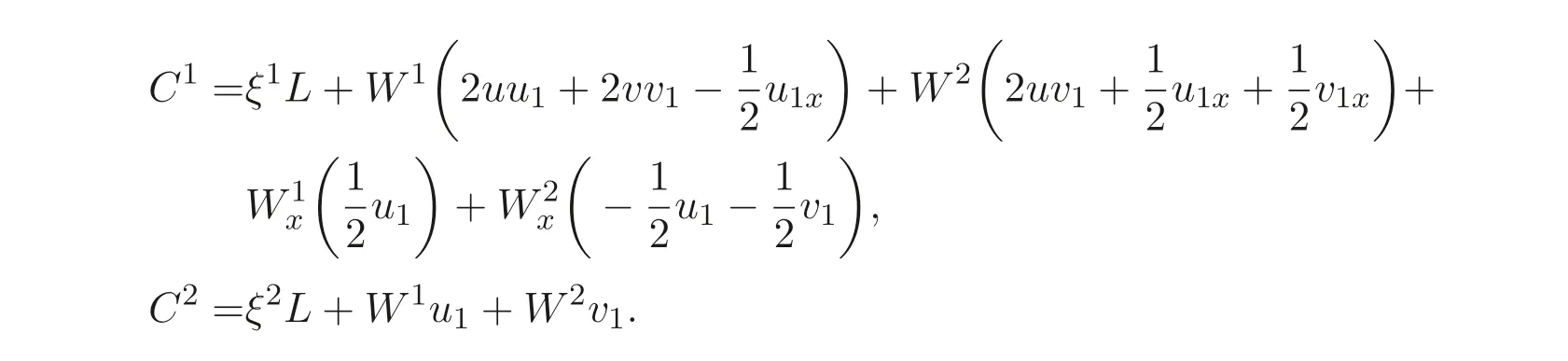
这里W1=η1−ξ1ux −ξ2ut,W2=η2−ξ1vx −ξ2vt.

下面分情况讨论.

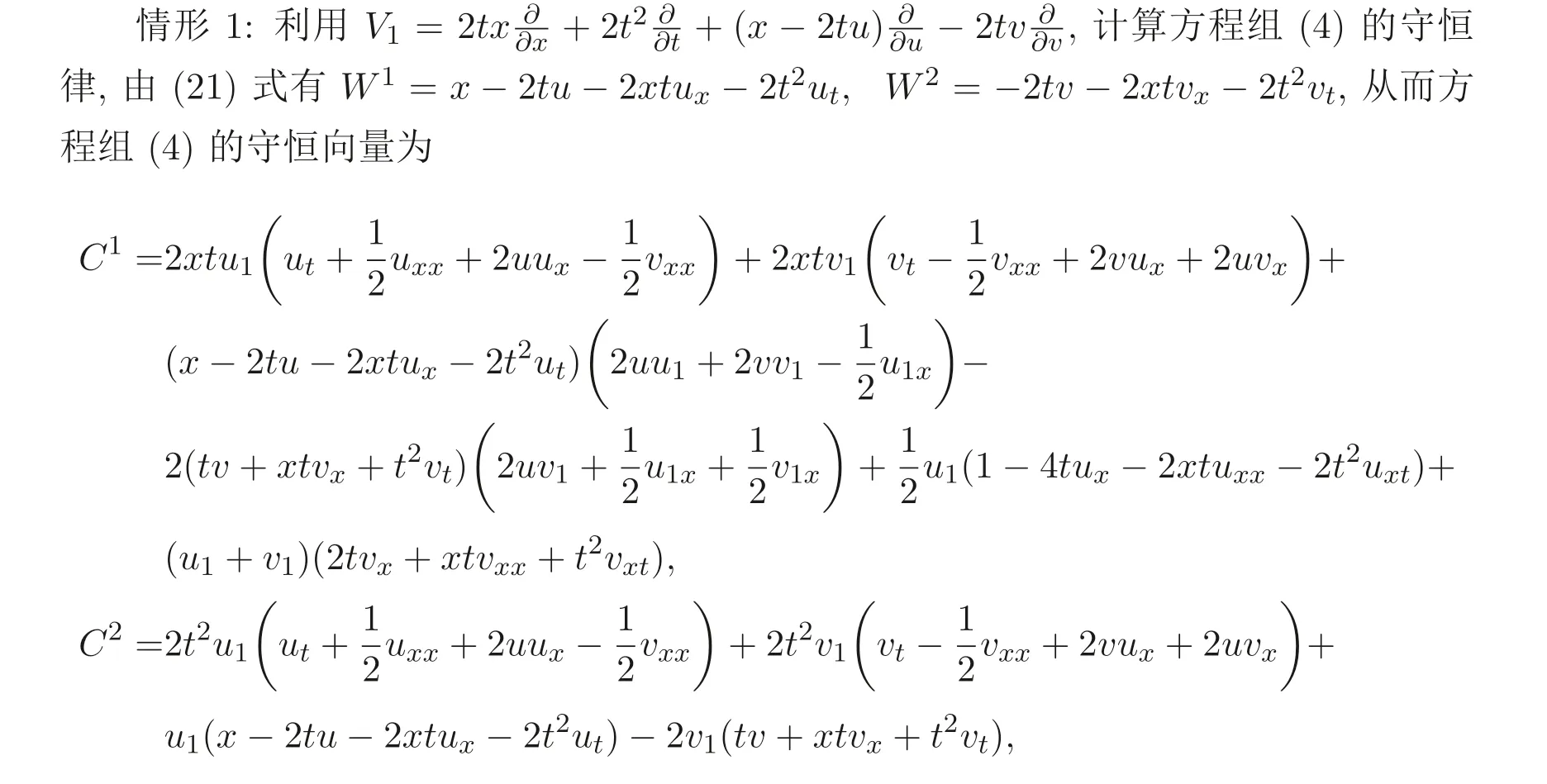
情形2: 利用

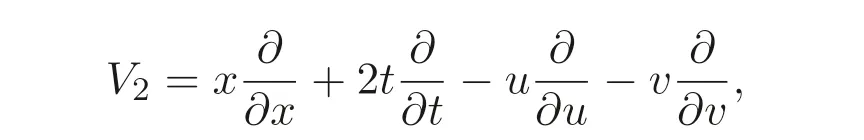
计算方程组(4) 的守恒律, 由(21) 式有

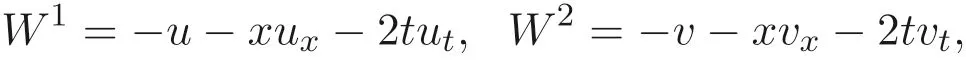
从而方程组(4) 的守恒向量为

通过上面的讨论, 发现每一种情况下求出的守恒向量都含有伴随方程中的任意函数u1,v1, 故给出了方程组(4) 的无穷多守恒律, 同时由符号计算工具Maple 验证了以上求出的守恒向量满足守恒律公式Dx(C1)+Dt(C2)=0.

5 结束语

文章证明mBKK 方程组(4) 的非线性自伴随性, 此性质为后续使用Ibragimov 定理奠定了基础. 通过对mBKK 方程进行李对称分析, 得到了其对应的李对称. 基于方程的对称性和其对应的伴随方程, 运用Ibragimov 定理, 构造了方程组(4) 对应的无穷多守恒律, 这对研究微分方程的可积性、线性性和求解方面有着非常重要的作用. 后续研究工作可将伴随方程的方法推广应用到其他的非线性偏微分方程的研究.