基于矩形有限元离散泊松方程的二重网格法研究
韩冰冰
(盘锦职业技术学院 基础部,辽宁 盘锦 124000)
0 引言
泊松方程是一类重要的椭圆型偏微分方程,广泛应用于电学、磁学、力学、热学、静电场问题、温度扩散问题等领域的研究与计算,在学科的基础理论研究中占有重要的地位。多重网格法是求解偏微分方程数值解常用的一类方法,可分为代数多重网格法和几何多重网格法,对于代数多重网格法,徐小文讨论了各向异性四边形网格下求解线性有限元方程的代数多重网格法[1]。李明等人针对三维泊松方程,采用四面体元离散,提出了一类代数两重网格法[2]。 目前,瀑布型多重网格法是几何多重网格法的研究热点之一。李郴良等人结合外推技巧提出了一类求解椭圆型方程的新的瀑布型多重网格法[3]。赵旺等人讨论了三次插值算子对瀑布型多重网格法的作用[4]。李明等人结合新外推公式和经典外推公式提出了基于外推公式的瀑布型多重网格法[5],并针对二次Lagrangian有限元方程,提出了一类瀑布型多重网格法[6]。禹海雄对几类非线性椭圆问题提出了一系列多重网格法[7]。本文基于前人的部分思想,针对选用合适的一对步长,使用矩形有限元离散泊松方程得到的粗网格方程及细网格方程,采用三次样条插值算子作为插值算子,选用共轭梯度法作为在细层上的磨光算子,提出基于矩形有限元格式的瀑布型二重网格法,针对不同粗细网格情况下给出了相应的数值实验。
1 相关方法概述
1.1 泊松方程的概述
1.1.1 泊松方程的矩形有限元离散
考虑如下二维泊松问题
{-Δu(x,y)=f(x,y),inΩu=0,on∂Ω
(1)

Auuh=Fh
(2)
1.1.2 共轭梯度迭代法
共轭梯度法(CG)[8]又称共轭斜量法是一种求解线性方程组的迭代格式,不必选择迭代参数而收敛速度快,广泛应用于求解对称正定方程组
Au=f
(3)
该算法的具体步骤如下:
第一步:给定初始向量u(0),计算
p(0)=r(0)=f-Au(0)
第二步:对于k=1,2,…,n有
p(k+1)=r(k+1)+βkp(k)
1.2 三次样条插值
插值算子的插值效率对瀑布型多重网格法有着重要的影响。文中使用三次样条插值作为插值算子。
1.2.1 三次样条函数的定义
定义1[8]若函数S(x)∈C2[a,b],且在每个小区间[xi,xi+1]上是三次多项式,其中xi∈[a,b],i=0,1,2,…,n是给定节点,则称节点x0,x1,…,xn上的三次样条函数。若在节点xi上给定函数值yi=f(xi)(i=0,1,…,n),且S(xi)=yi(i=0,1,2,…,n)成立,则称S(x)为三次样条插值函数。
定义2 已知yi=f(xi),其中xi∈[a,b],i=0,1,2,…,n,S(x)是[a,b]上的函数,若满足
1)S(xi)=f(xi),i=0,1,2,…,n;
2)Sk(x)=S(x)|[xk-1,xk]为三次多项式;
3)S(x)∈C2[a,b],二阶导数(S″(x))连续,一阶导数(S′(x))相等,
则称S(x)为三次样条插值函数。
1.2.2 三次样条插值算子S(x)的构造
采用待定系数法构造S(x),设Sk(x)=akx3+bkx2+ckx+dk,即

从定义2可知,要求出S(x),在每个小区间[xi,xi+1]上要确定4个待定系数,共有n个小区间,故应确定4n个参数,于是S(x)有4n个待定系数,需构造4n个方程即可确定S(x)。因条件1)有n+1个方程,条件3)为
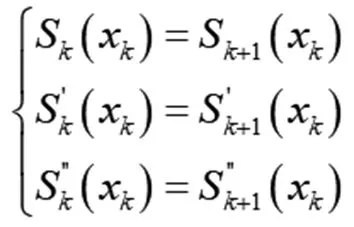
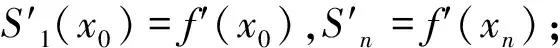
1.3 瀑布型二重网格法改进

2 数值实验
为了检验该算法的有效性及其插值算子的效率,选用的对比算法也为瀑布型两重网格法,其插值算子为线性插值。两种算法的粗细网格相同,磨光算子都为共轭梯度法。使用矩形有限元法离散以下算例,形成对应的粗细网格空间。为便于描述,约定如下标记:“误差”表示采用算法求出的数值解与问题的真解的2-范数误差,“步数”表示用CG磨光次数,“时间”表示迭代所需要的时间(单位:秒),“k”表示粗网格步长与细网格步长之比,即k=H/h。
算例1
f(x,y)=sin(y)ex(1-x2)(1-y2)-4sin(y)exx(1-y2)+2sin(y)(1-ex)(1-y2)+sin(y)(1-ex)(1-x2)(1-y2)+4cos(y)(1-ex)(1-x2)y+2sin(y)(1-ex)(1-x2)
真解为:u(x,y)=sin(y)(1-ex)(1-x2)(1-y2);Ω=(0,1)×(0,1)。

表1 对比算法与改进算法对算例1的数值结果
算例2
f(x,y)=2π(2sin(x2π)x2πsin(y2π)
-cos(x2π)sin(y2π)+2sin(x2π)sin(y2π)y2π
-sin(x2π)cos(y2π))
真解为:u(x,y)=sin(x2π)sin(y2π);Ω=(0,1)×(0,1)。
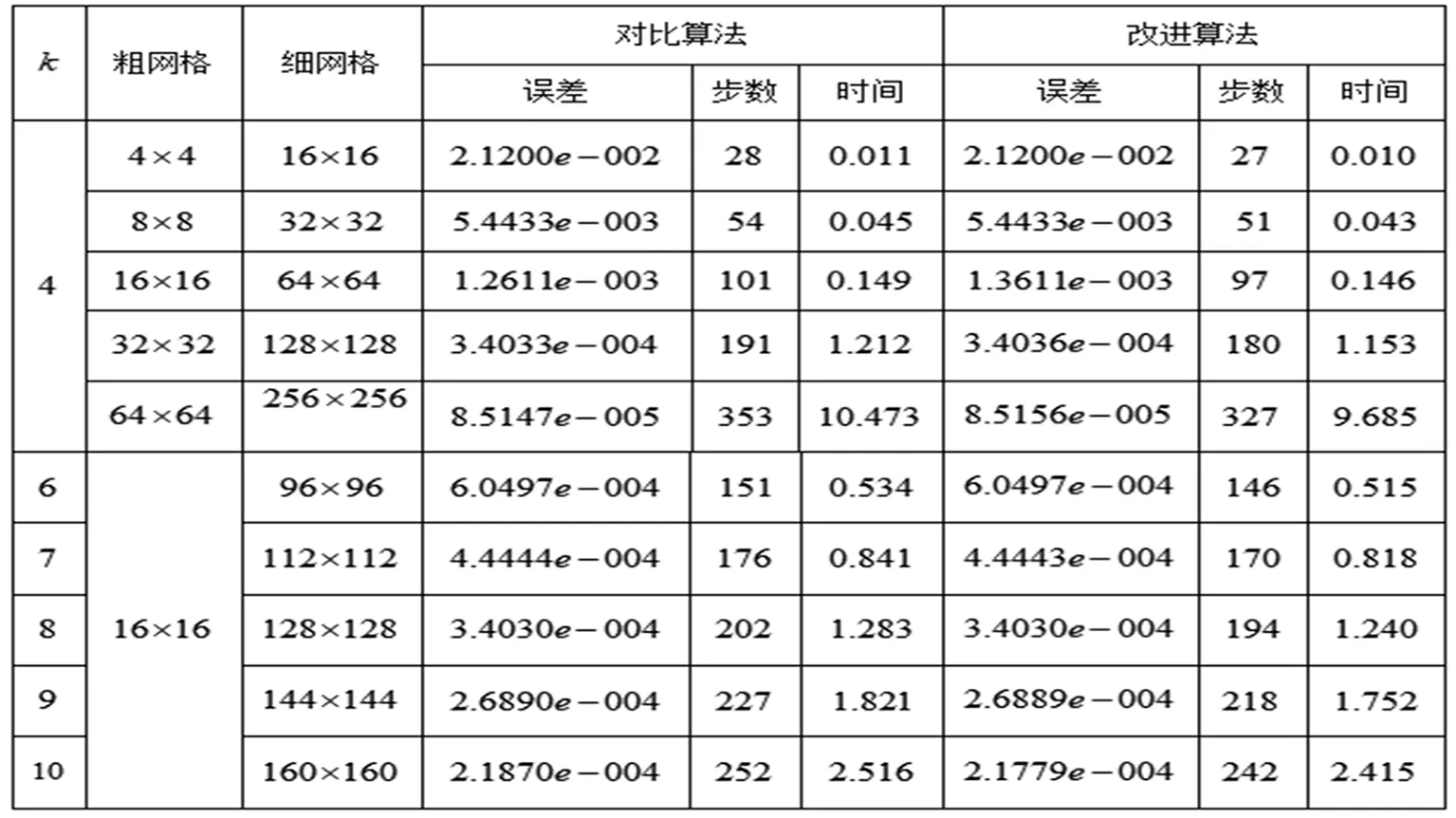
表2 对比算法与改进算法对算例2的数值结果
由表1和表2可以看出,只需要使用节点较少的粗网格插值算子、磨光算子就能有效求出节点较多细网格上的数值解,从数值结果可以看出,使用不同的插值算子细层网格上的磨光步数有所不同。与对比算法相比较,改进算法的计算时间要更短一些。数值实验表明,该算法能有效求解矩形有限元格式下二维泊松方程的数值解。
3 结论
并非所有的泊松方程都有解析解,因此寻求高精度的数值解成为目前研究的重要内容之一。文中采用矩形有限元方法离散泊松方程,形成粗网格和细网格,对粗网格精确求解,然后采用三次样条插值为细层提供初始值,构造出一类求解二维泊松方程的瀑布型二重网格法,并结合数值实验讨论不同粗细网格情况下算法的计算效率。

