例谈依托函数图象培养几何直观能力

天津市滨海新区汉沽教育中心(300480) 白绍强

几何直观就是依托、利用图形进行数学的思考和想象,产生对数量关系的直接感知.借助几何直观可以把复杂的数学问题变得简明、形象,有助于探索解决问题的思路.直观是想象的基础,依托直观才能抽象出研究对象的本质属性,才使数学思考、逻辑推理成为有源之水、有本之木.

函数的图象反映了两个变量间的对应关系和变化规律.从函数图象的形象关系得出抽象的数量关系,此类问题学生的解决经验还略显不足.本文将从函数图象出发,数形结合地进行思维,通过观察、思考并计算、推理得出有关结论,丰富学生的问题解决策略,提高学生的几何直观能力.

例1 (2020 年天津市中考试题) (12) 已知抛物线y=ax2+bx+c(a,b,c是常数,a0,c ＞1) 经过点(2,0),其对称轴是直线x=.有下列结论:①abc ＞0;②关于x的方程ax2+bx+c=a有两个不等的实数根;③a ＜-.其中,正确结论的个数是( ).

A.0 B.1 C.2 D.3

1 根据已知条件,画出函数图形

培养几何直观能力,首先要养成画图的习惯,直观确认图形的特性,看出看到图形的基本要素之间的位置关系和数量关系.此类问题从已知条件出发,抛物线的形状、开口大小和位置还不确定,就要画出图形,也就是函数的图象,利用图象可将相对抽象的思考“图形化”、“直观化”,为理解概念、寻求解题思路带来便利,特别是初中阶段学生的思维方式还是以形象思维为主,计算、证明、逻辑推理都是在形象思维的基础上进行的,所以依据问题的已知信息,正确画出函数的图象(草图)成为问题解决的关键.本题函数的图象如图1.

图1

函数的图象以几何的形式直观地表示了两个变量间的单值对应关系,是研究函数的重要工具.自变量与函数的每对对应值分别是点的横、纵坐标.教给学生以图象为工具来研究函数,形成数形结合的研究问题的思想.

2 利用图象信息,强化直观认识

函数解析式与函数图象两者密切联系,解析法从数量关系的角度明确自变量和函数的对应关系,我们可以从数与式的角度来研究函数的性质,而图象法可直观地反映函数的变化规律、变化趋势.研究函数时二者要紧密结合,由数到形,由形到数.此类问题要关注图象的相关信息,熟悉研究图象的方法,感悟图象给我们研究问题带来的好处.

2.1 图象关键要素

例1 的抛物线开口向下,可知a ＜0;根据左同右异的规律,可得b ＞0,故abc ＜0;由对称性可知抛物线与x轴的另一交点坐标为(-1,0),抛物线的解析式为y=a(x+1)(x-2)=ax2-ax-2a,可知b=-a,c=-2a,abc=2a3,也可得abc ＜0.

2.2 图象关键点

例1 的抛物线经过点(2,0),可得4a+2b+c=0;抛物线经过点(-1,0),可得a -b+c=0;顶点坐标为这些代数式或等量关系可由图象直接看到得到,为其他问题的解决奠定了基础.例1 中②的解决有如下方法:

方法1:如图2,从函数图象看,方程ax2+bx+c=a根的情况就是直线y=a(a ＜0) 与抛物线y=ax2+bx+c的交点情况,两个交点的横坐标m和n就是方程的根.

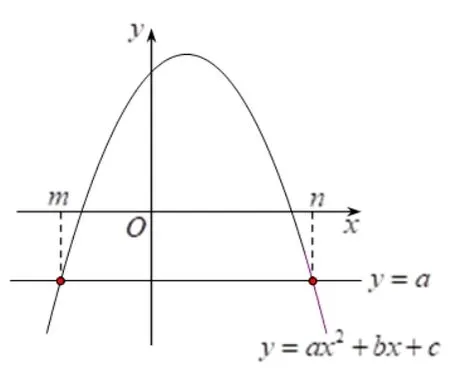
图2

方法2:从图象角度看,方程ax2+bx+c-a=0 的根就是抛物线y=ax2+bx+c-a与x轴交点的横坐标.从解析式的角度分析,因为-a ＞0,所以将抛物线y=ax2+bx+c向上平移-a个单位就得到了抛物线y=ax2+bx+c-a,此抛物线与x轴一定有两个交点,所以方程有两个不等的实数根.

方法3:从方程角度看,方程ax2+bx+c-a=0 转化为方程ax2-ax-3a=0,其判别式Δ=(-a)2-4a·(-3a)=13a2＞0,故方程有两个不等的实数根.

方法4:抛物线的解析式为y=ax2 -ax-2a,解方程a(x2-x-2)=a,解得x=,所以方程有两个不等的实数根.

3 建立数形联系,丰富思考问题方式

函数内容具有“双重性”,既有数的特征,也有形的特征,我们要从两个方面来认识它,才能变得形象生动,学生学起来易于接受,运用它们去思考解决问题,形成几何直观能力.一些数学知识之间存在关联和逻辑顺序,函数、方程和不等式存在着实质性的联系.从函数的观点看方程、不等式,是对方程、不等式知识的再分析再认识,是以新的视角、新的高度居高临下地进行动态分析,是对方程、不等式知识进行整合.函数对方程、不等式具有统领作用,要加强知识间的横向和纵向的联系,注意对函数、方程和不等式内容的整体建构.

例2 (2019 年天津中考题第(12) 题) 二次函数y=ax2+bx+c(a,b,c是常数,0)的自变量x与函数值y的部分对应值如下表:

且当x=-时,与其对应的函数值y ＞0.有下列结论:

A.0 B.1 C.2 D.3

从数的特征出发,表格中给出了自变量和函数的五组对应值,自变量与函数的单值对应关系一目了然,这也正是用列表法表示函数关系的优点所在.根据已知条件,可画出函数大致图象(图3).

图3

图3

3.1 从数和形两个方面思考

已知函数值求相应的自变量的值需解方程.例2把x=0 时,y=-2和x=1 时,y=-2 代入函数解析式,可得b=-a,所以抛物线的解析式为y=ax2-ax-2,-2是关于x的方程ax2+bx+c=t的根,可得t=6a-2.把x=3 代入方程ax2-ax-2=6a-2 成立,3 是关于x的方程ax2+bx+c=t的两个根.

从形的特征来看,例2 中点(0,-2)和(1,-2)关于对称轴对称,可知对称轴为x=,所以点(-2,t)和点(3,s)是抛物线上关于其对称轴对称的两个点,有t=s,所以3 是关于x的方程ax2+bx+c=t的根.

3.2 相关知识整体建构

数量关系包含相等关系和不等关系,在初中阶段仅在七年级下册学习了一元一次不等式与不等式组,与较多研究的相等关系(方程与方程组)即有联系也有区别,根据不等式的性质,对不等式进行由繁至简的变形能力还显不足,需要教师的补充和强化,为学生的后续知识的学习奠定基础.

3.2.1 由字母间的关系得出未知字母的范围

例1 中③的解决可如下进行

3.2.2 利用函数的增减性判断代数式的范围

4 关联问题推理,提升几何直观层次

培养几何直观能力,不仅是从看到的展开想象、思考,还能从关联的、综合的情境中,直观地发现、猜想结论,进而去计算、证明结论.几何直观是合情推理的重要基础.

依托函数的图象,判断关于a,b,c代数式的符号是常见问题.不等式的性质是解不等式的基础,是不等式变形的依据,从运算的角度在不等式的两边同时进行同样的变化,来确定不等号的方向是否改变.教师要以不等式的变形为知识载体,渗透和点播其中蕴涵的消元、转化的数学思想,在思想指导下进行不等式的变形.

例3 (2020 年广东省中考试题第(10) 题) 如图,抛物线y=ax2+bx+c的对称轴是x=1,下列结论:①abc ＞0;②b2-4ac ＞0;③8a+c ＜0;④5a+b+2c ＞0,正确的有( ).

A.4 个 B.3 个 C.2 个 D.1个

例3中③的解决可如下进行:由-=1得b=-2a,由图象可知,当x=-2 时,相应的函数值4a-2b+c ＜0,把b=-2a代入可得8a+c ＜0.此题把字母间的关系代入不等关系,起到了消元的作用.

例3 中④的解决可如下进行:由图象可知,当x=-1时,相应的函数值a-b+c ＞0,当x=3 时,相应的函数值9a+3b+c ＞0,两不等式相加可得10a+2b+2c ＞0,不等式两边都除以2 得:5a+b+c ＞0,又c ＞0,两不等式相加可得5a+b+2c ＞0.

数学家华罗庚曾告诉我们:“数形结合百般好,隔离分家万事休”.将抽象问题具体化、形象化,代数问题几何化,教给学生学会从“数”与“形”两个角度来认识数学,逐渐养成数与形之间的划归与转化的意识,借助数的精确来认识图形的细微之处、特殊之处,借助形的性质及位置来推理数量关系,把数量关系和直观图形结合起来,整体性地认识数学知识内部结构,使学生认识到几何直观在数学学习过程中的作用.学会这种数学的思考方式和学习方式,促进学生较好地理解数学本质,无疑会对学生创新意识的发展、解决问题能力的提升和数学学科素养的培育,具有十分重要的意义.