对“直线与平面所成角”复习的教学思考
浙江省台州市第一中学(318000) 曹贤鸣 陈亚菲
求直线与平面所成角大小问题,是立体几何中的重点问题之一.课堂观察和作业批改中发现:求解直线与平面所成角大小问题时,绝大部分学生习惯于运用向量建系法或等体积法求解此类问题.他们认为:用向量建系法,思路简单,可以程序化求解;用等体积法,利用几何体的体积相等进行距离之间的转换,无须考虑垂线的垂足的具体位置,可简化求解思路.由于习惯了这两种求法,大部分学生解题时往往忽略了几何法的存在.但有些题,在求解过程中不易找出两两垂直的三条直线,如果强行建系,会增加运算量,甚至因运算繁琐导致半途而废;而一些不易求出点与面之间距离的题,等体积法也无用武之地.这就要求教师在复习直线与平面所成角求法时,在巩固向量建系法和等体积法之后,还要回归到综合几何法的复习.通过对几何法的训练,完善学生求解直线与平面所成角的方法,帮助学生完善立体几何中点、线、面之间的知识体系和方法体系.
1 对“线面角”复习的思考
用代数的运算解决几何问题是现代数学的重要研究手段,所以运用向量法求解立体几何中的相关问题是课堂教学的主流.课标解读指出,“学生除了掌握用代数方法解决几何问题外,还要学会在几何中为代数问题寻找直观背景的方法”.所以“空间几何与代数的教学中,在培养学生直观想象素养的同时,也要重视逻辑推理的教学.代数为几何提供研究方法,几何为代数提供直观背景,两者相互渗透,有助于提高学生的逻辑推理能力”.
因此,高三复习时,在完成了用坐标法和等体积法求解直线与平面所成角的复习之后,还要适当补充综合几何法的求解方法.通过综合应用知识的训练,沟通知识之间的联系和规律;帮助学生理清知识的来龙去脉,理解问题的几何背景.通过多种解法后的反思,让同学们弄清综合几何法、向量坐标法和等体积法的联系与区别,确保具体操作时能迅速而准确地选用合适的求解方法.
2 综合几何法求解“线面角”的教学实践
利用几何法求解直线与平面所成角问题的本质是利用已知条件、定理、性质实现立体几何问题平面化.其中最为关键的是找出目标平面的一条合适的垂线,有了垂线就有了垂足,垂足与斜足之间的连线就是直线在平面内的射影.这样构造出的斜线与射影所成的平面角就是这条直线与平面所成角.垂面法是求解直线与平面所成角问题的常用方法之一,根据教学实践,垂面法是寻找目标平面的垂线时的一种有效的方法,先寻找出直线与平面所成角的目标平面的一个垂面,然后在寻找到的垂面内作出它与目标平面的交线的一条垂线,那么这条直线就垂直于目标平面.下面以近几年浙江高考题为例,说明利用这一数学模型求解直线与平面所成角问题的具体方法.
题1 (2018 年浙江高考题)如图,已知多面体ABC -A1B1C1,AA1、BB1、CC1均垂直于平面ABC,∠ABC=120°,AA1=4,CC1=1,AB=BC=BB1=2.
(Ⅰ)证明:AB1⊥平面A1B1C1;

(Ⅱ)求直线AC1与平面ABB1所成角的正弦值.
分析与求解:(Ⅰ)略;
(Ⅱ) 已知AA1、BB1、CC1均垂直于平面ABC,所以AA1与BB1共面,因此平面ABB1就是平面ABB1A1.
(1)寻找目标平面ABB1也就是平面ABB1A1一个垂面,就是要找到与平面ABB1内一条直线垂直的平面,由(Ⅰ)结论:平面ABB1内的直线AB1⊥平面A1B1C1,那么平面ABB1⊥平面A1B1C1.

题2 (2019 年浙江高考题)如图,已知三棱柱ABC -A1B1C1,平面A1AC1C⊥平面ABC,∠ABC=90°,∠BAC=30°,AA1=A1C=AC,E,F分别为AC,A1B1的中点.

(Ⅰ)证明:EF⊥BC;
(Ⅱ)求直线EF与平面A1BC所成角的余弦值.
分析与求解:(Ⅰ)题目中垂直信息:
(1)等边ΔAA1C中,AE=EC,则A1E⊥AC;结合平面A1AC1C⊥平面ABC,且平面A1AC1C∩平面ABC=AC,那么A1E⊥平面ABC.
(2)由∠ABC=90°得AB⊥BC.三棱柱中AB//A1B1,则有BC⊥A1B1.由(1)结论有BC⊥A1E,又A1E∩A1B1=A1得BC⊥平面A1B1E,进而可得EF⊥BC.
(Ⅱ) 先寻找平面A1BC内一条直线垂直的一个平面,(Ⅰ)的(2)中有平面A1BC内一条直线BC⊥平面A1B1E,那么平面A1BC⊥平面A1B1E.只要在平面A1B1E内的直线EF上取一点作平面A1B1E与平面A1BC的交线的垂线,此线就是平面A1BC的垂线.图中两平面无交线,将平面延展作出其交线.取BC中点G,连EG、GF,易知四边形EGFA1是平行四边形,所以平面A1B1E就是平面EGFA1,此时平面EGFA1∩平面A1BC=A1G.由A1E⊥平面ABC,EG ⊆平面ABC,则A1E⊥EG,所以四边形EGFA1是矩形.在平面EGFA1内过E作A1G的垂线,此时EF在平面A1BC上的射影在直线A1G上,所以∠EOG(或其补角)是直线EF与平面A1BC所成角.

题3 (2017 年浙江高考题)如图,已知四棱锥P -ABCD,ΔPAD是以AD为斜边的等腰直角三角形,BC//AD,CD⊥AD,PC=AD=2DC=2CB,E为PD的中点.
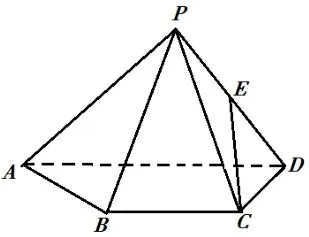
(Ⅰ)证明:CE//平面PAB;
(Ⅱ)求直线CE与平面PBC所成角的正弦值.
分析与求解:(Ⅰ)略;
(Ⅱ)题目中垂直信息:
(1) ΔPAD是以AD为斜边的等腰直角三角形PA⊥PD;取AD的中点N,则PN⊥AD;结合BC//AD得PN⊥BC.
(2)底面ABCD中CD⊥AD,且AD=2DC=2CB,四边形BCND是一个矩形,所以BN⊥AD,BN⊥BC,CD⊥BC.目标:寻找平面PBC内的一条直线垂直的一个垂面.
(i)垂直信息中垂直的条件相对集中于平面PBC内的“直线BC”,垂直于BC的平面就垂直于平面PBC.
(ii)由垂直信息(1)中PN⊥BC和(2)中BN⊥BC.可得BC⊥平面PBN,又BC ⊆平面PBC,所以平面PBC⊥平面PBN.
因此,只要在平面PBN作这两平面的交线PB的垂线,那么所作直线就是平面PBC的一条垂线.
本题与题1、题2 不同的是前两题中的“线面角”的直线中有点在所构造的垂面内,而本题中的直线CE与平面PBC的交点为C,线段CE上除点C外没有点在平面PBN内,不能直接利用前面的模型求解.
如果将直线CE平移使之与平面PBN产生交点,即在平面PBN内作直线CE的平行线,利用两条平行线与一个平面所成角相等,就能将问题转化为前面所提的模型求解了.
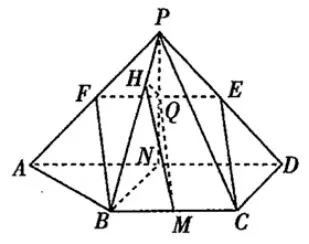
取PA中点F,得到平行四边形BCEF,设EF ∩PN=Q,由于E为PD的中点,PN是AD的中垂线,所以Q为EF的中点;在平行四边形BCEF中,CE//QM,直线QM与平面PBC所成角就等于直线CE与平面PBC所成角了.在平面PBN内过Q作QH⊥PB,则QH⊥平面PBC,连HM,则∠QHM是直线QM与平面PBC所成角.


求解直线与平面所成角问题的关键是寻找目标平面的一条合适的垂线,所以解题时要尽可能挖掘题中垂直的信息,关注垂直信息中与目标平面垂直的直线,找出与目标平面垂直的平面.由以上三个题目的求解可以看到,与目标平面垂直的平面的出现是多样化的.如题1 中目标平面的垂面的信息来自于第(Ⅰ)题的结论;题2 中目标平面的垂面的信息来自于第(Ⅰ)题的证明过程;虽然在题3 中寻找到的目标平面的垂面中,除直线与平面交点外再无其他交点,但通过适当的平移,仍可将该题转化为适用于以上模型求解的问题,进而求解.
3 结束语
复习时,如果满足于等体积法和向量建系法,就会造成学生空间想象能力和逻辑推理能力的缺失,不利于他们领悟蕴含其中的数学思想方法,也不利于他们数学活动经验的积累.复习求解“线面角”问题时,我们既要重视深受学生喜欢的等体积法和向量建系的教学,也要在他们掌握这两种方法的基础上,鼓励学生回归几何法,通过几何法提高学生的直观想象能力和逻辑推理能力,通过向量建系法、等体积法的代数法提升学生的数学运算能力,进而培养和发展学生的数学核心素养.

