四色猜想的简洁证明

田永成

(东北大学，辽宁 沈阳 110004)

0 引言

四色猜想是国际数学界疑存一百多年的数学难题，虽然在1976年，APPel和HaKen等利用电子计算机花了1260多机时证明了四色猜想，但是从数学家的价值观看来，对四色猜想给出简洁的理论证明还是十分必要的，这一问题的解决正说明数学难题用数学推理解决是完全可能的[2]。

本文只考虑简单平面图。若一个平面图G的所有顶点均在它的同一个面的边界上，则称G是一个外平面图，若对一个(外)平面图G中任意两个不邻接的点u、v，G+uv均不是(外)平面图，则称G是一个极大(外)平面图。未加说明的术语和记号参见参考文献[1]。

1 四色猜想的证明

为了证明方便，先给出以下引理和定理：

引理1[1]若G是n(≥4)阶极大平面图，则3≤δ(G)≤5。

引理2[1]若G是n(≥4)阶极大平面图有e条边，则e=3n-6。

引理3[3]每一个2连通平面图可以嵌入平面使任何一个特定的面成为外部面。

定理1[1]以下三个命题是等价的：

(i)每个平面图都是4顶点可着色的；

(ii)每个平面图都是4面可着色的；

(iii)每个简单2边连通3正则平面图都是3边可着色的。

定理2 设G是n(≥6)阶δ(G)=4的极大平面图，则G存在4阶极大外平面子图是3点可着色的，由此子图开始3点着色，可推出G是4点可着色的。

证对G的阶数n(≥6)用数学归纳法证明：当n=6(6是4正则极大平面图的阶数)时可直接验证定理2成立。由引理2可知δ(G)=4不小于7阶的极大平面图G，至少有1个不小于5度的点，n=7时不存在有1个6度点的δ(G)=4的7阶极大平面图G，只存在2个5度点，它们的距离为2的7阶极大平面图，此图是唯一的，如图2.1G；若有1个3度点，3个5度点(其余的为4度点)，该3度点与5度点均邻接的7阶极大平面图G，此图也是唯一的，如图2.2G。

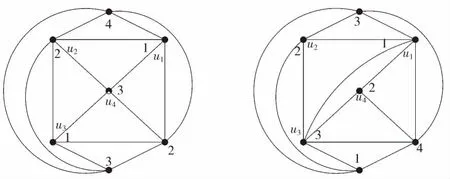
图2.1 G 图2.2 G

当n=7时可直接验证定理2成立：在图2.1G中取由u1，u2，u3，u4为顶点的G的4阶极大外平面子图开始进行3点着色，其中d(u4)=4，进而推出G是4点着色的，如图2.1G；在图2.2G中取由u1，u2，u3，u4为顶点的G的4阶极大外平面子图开始进行3点着色，其中d(u4)=3，进而推出G是4点可着色的，如图2.2G；由图2.1G、图2.2G的4点着色过程可知：无论点u4的度数是否小于4都能推出G是4点可着色的。由引理3不防设G的最小度点u位于G的内部面内，以下同。

假设n-1(n≥8)时定理2成立，证明n时定理2也成立。

设G是n(n≥8)阶δ(G)=4的极大平面图，如图2.3G；由前述分析知，在G中选择1点u，它至少与G中1个不小于5度点如u2邻接，d(u)=4，N(u)=﹛u1，u2，u3，u4﹜⊂V(G)，即d(u2)≥5。

从G中移去点u和与它关联的边，再连接边u1u3，得n-1阶极大平面图G1，如图2.4G1其中d(u4)≥4或d(u4)=3；若G1中d(u4)≥4，G1是满足定理2假设条件的n-1阶极大平面图，故从G1的以u1，u2，u3，u4为顶点的4阶极大外平面子图开始3点着色，进而推出G1是4点可着色的，如图2.4G1；若G1中d(u4)=3，由前述分析，图2.2G知：从G1的以u1，u2，u3，u4为顶点的4阶极大外平面子图开始3点着色，进而推出G1是4点可着色的，如图2.4G1。

将G1中的边u1u3移去，在以u1u2u3u4u1为边界的面内添一点u，并连接边u1u，u2u，u3u，u4u得满足定理2条件的n阶极大平面图G，原G1中的点的着色不变，点u着4色，G是4点可着色的，以u，u2，u3，u4为顶点的G的4阶极大外平面子图是3点可着色的，如图2.5G，故定理2成立，证毕。

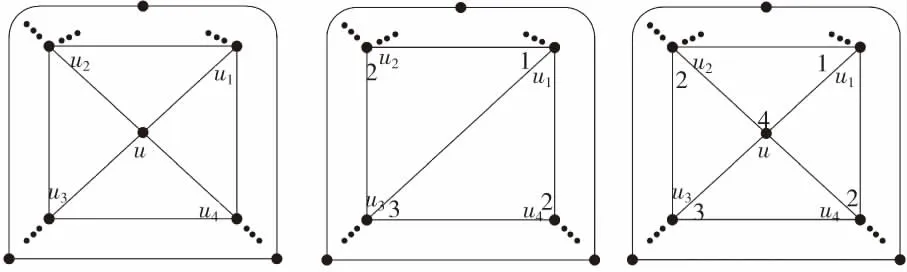
图2.3 G 图2.4 G1 图2.5 G

定理3 设G是n(≥12)阶δ(G)=5的极大平面图，则G存在5阶极大外平面子图是3点可着色的，由此子图开始3点着色，可推出G是4点可着色的。

证对G的阶数n(≥12)用数学归纳法证明：当n=12(12是5正则极大平面图的阶数)时可直接验证定理3成立。δ(G)=5的13阶极大平面图不存在；由引理2知，δ(G)=5不小于14阶的极大平面图G至少有1个不小于6度的点，n=14时不存在有1个7度点的δ(G)=5的14阶极大平面图，只存在2个6度点的距离为3的极大平面图G，如图3.1G，此图是唯一的；若有1个4度点，3个6度点，该4度点与2个6度点邻接与1个6度点的距离为2，此图也是唯一的，如图3.2G。当n=14时，可直接验证定理3成立：在图3.1G中取以u1，u2，u3，u4，u5为顶点的G的5阶极大外平面子图开始进行3点着色，其中d(u5)=5，进而推出G是4点可着色的，如图3.1G；在图3.2G中取以u1，u2，u3，u4，u5为顶点的5阶极大外平面子图开始3点着色，其中d(u5)=4，进而推出G是4点可着色的，如图3.2G；由图3.1G、图3.2G的4点着色过程可知，无论点u5的度数是否小于5都能推出G是4点可着色的。

假设n-1(n≥15)时定理3成立，证明n时定理3也成立。

设G是n(n≥15)阶δ(G)=5的极大平面图，如图3.3G；由前述分析知，在G中选择1点u，它至少与G中1个不小于6度点如u2邻接，d(u)=5，N(u)=﹛u1，u2，u3，u4，u5﹜⊂V(G)，即d(u2)≥6。从G中移去点u和与它关联的边，再连接边u1u3，u1u4，得n-1阶极大平面图G1，如图3.4G1，其中d(u5)≥5或d(u5)=4；若在G1中d(u5)≥5，G1是满足定理3假设条件的n-1阶极大平面图，如图3.4G1，从G1的以u1，u2，u3，u4，u5为顶点的5阶极大外平面子图开始3点着色，进而推出G1是4点可着色的，如图3.4G1；若在G1中d(u5)=4，由前述分析，图3.2G知：从G1的以u1，u2，u3，u4，u5为顶点的5阶极大外平面子图开始进行3点着色，进而推出G1是4点可着色的，如图3.4G1。

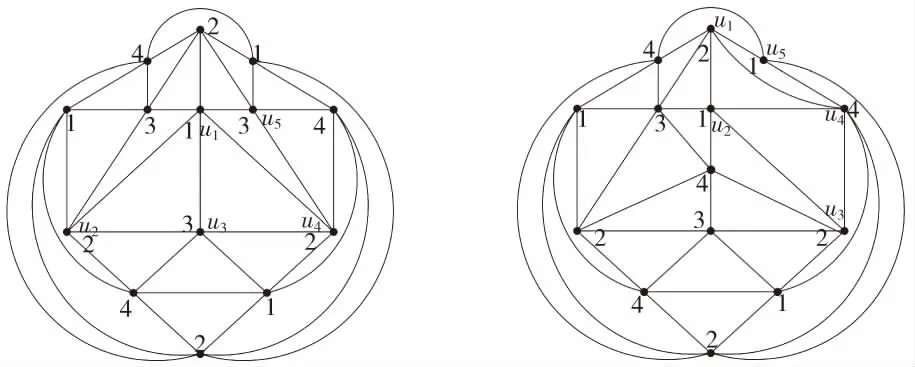
图3.1 G 图3.2 G

将G1中的边u1u3，u1u4移去，在以u1u2u3u4u5u1为边界的面内添一点u，并连接边u1u，u2u，u3u，u4u，u5u得满足定理3条件的n阶极大平面图G，原G1中点的着色不变，点u着4色，G是4点可着色的，以u，u2，u3，u4，u5为顶点的G的5阶极大外平面子图是3点可着色的，如图3.5G，故定理3成立，证毕。

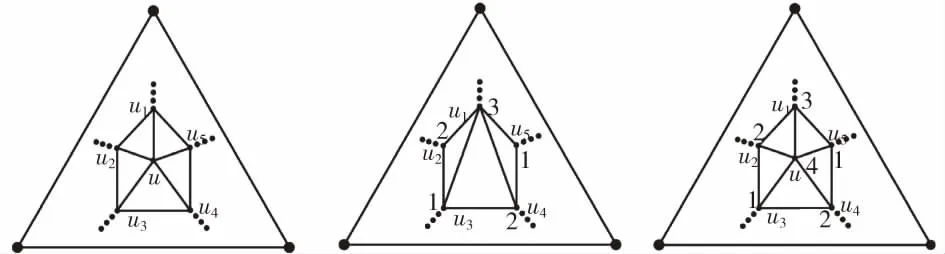
图3.3 G 图3.4 G1 图3.5 G

定理4 设G是n(≥4)阶极大平面图，则G是4点可着色的。

证对G的阶数n(≥4)用数学归纳法证明：当n=4、5时可直接验证定理4成立。

假设n-1(n≥6)时定理4成立，证明n时定理4也成立。

设G是n(≥6)阶极大平面图，由引理1分以下3种情形证明：

δ(G)=3，G中存在1点u，d(u)=3，N(u)=﹛u1，u2，u3﹜⊂V(G)，如图4.1G。从G中移去点u得n-1阶极大平面图G1，如图4.2G1，由假设知G1是4点可着色的，u1，u2，u3分别着1、2、3色，如图4.2G1；在G1中由u1u2u3u1所围成的面内添1点u，并连接边u1u，u2u，u3u得n阶极大平面图G，原G1中点的着色不变，u着4色，则G是4点可着色的，如图4.3G，此时定理4成立；

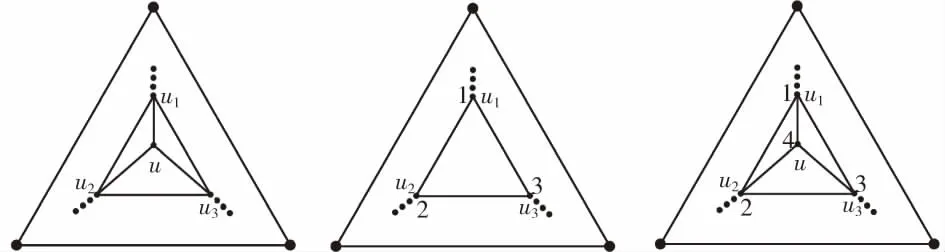
图4.1 G 图4.2 G1 图4.3 G

由定理2、定理3知δ(G)=4，δ(G)=5时定理4也成立，证毕。

定理5(四色定理)设G是n(≥4)阶简单平面图，则G是4面可着色的。

证由定理4及定理1的(i)，(ii)可证定理5成立，因而四色猜想是正确的。证毕。