优化问题解决策略，提升逻辑推理素养

[摘  要] 逻辑推理是学生发现问题，提出问题，多角度探索论证思路，促进理性思维走向理性精神的重要方式，也是学生构建数学知识体系，提升有逻辑、有条理思考和解决数学问题的必备能力. 文章以一道初中几何问题的解答为例，探讨了初中数学教学中培养学生逻辑推理素养的策略.

[关键词] 问题解决;逻辑推理;初中几何

逻辑推理贯穿整个初中数学教学过程，而提升逻辑推理能力对于提升学生的思维能力和思维品质具有重要的意义. 根据逻辑推理方式的不同，逻辑推理可分为合情推理和演绎推理两种形式，其中前者的命题范围是由小到大，其主要作用是发现结论，结果是或然的，而后者的命题范围是由大到小，其主要作用是证明结论，结果是必然的. 初中的学生正处于从“形象思维”向“逻辑思维”转变的关键阶段，在初中阶段提升学生的逻辑素养，其合情和演绎两种逻辑推理形式都不可偏废[1]，因此，下文以一道几何问题的解答为例，深入探究逻辑推理素养如何在初中数学问题解决中生根落地.

例题呈现及题意分析

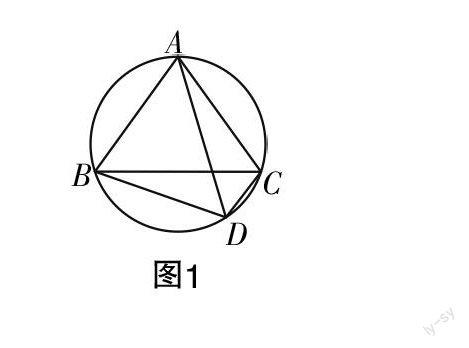
如图1所示，圓外接于△ABC，其中AB=AC，若D为弧BC上的一动点，然后连接BD，CD，AD，试求BD，CD，AD之间的数量关系. 若要获得具体的数量关系，还需要满足或者添加什么条件？

在初中数学教学中，有关图形与几何领域的问题基本上都是围绕基本图形、图形变化以及图形的性质与判定来开展的，其解题过程本身就是一个蕴含合情推理和演绎推理的推理过程，在一定程度上可以认为是促进学生思维品质和推理能力的良好载体. 而上述所呈现的例题，对于初中学生而言，解答这类动点几何问题是比较困难的，究其原因：一是点D是弧BC上的一动点，所求解的BD，CD，AD的长度是不断变化的;二是BD，CD，AD三者之间的数量关系较为复杂，并且目标并不明确;三是这是一个综合性开放问题，条件、结论以及解题策略都需要自己寻找.

解题策略及解法感悟

问题解决过程就是信息解构与知识建构的过程，在有关图形与几何领域的问题教学实践中，教师应从具体问题情境中解析其已知条件、求证结论，即首先通过类比、归纳等合情推理方式探索论证解题思路，理解其中所蕴含的数学思想和数学方法，在此基础上，再通过演绎推理验证结果的合理性，不断优化推理方法和逻辑推理思路[2].

1. 特殊情况

对于这种数量关系不明确的题目，教师应及时引导学生采取“猜想—验证—证明”的方式，从一些特殊情况入手进行解答. 由于题目中的已知条件就是△ABC是等腰三角形，因此，不妨从这一条件入手，找到BD，CD，AD这三者之间的数量关系，再从变量和不变量角度出发，归纳总结出一般性的结论.

（1）△ABC是等边三角形

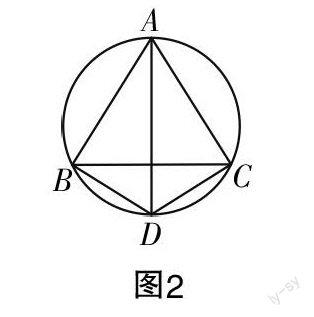
当AB=AC=BC时，我们不妨选取D为弧BC的中点，如图2所示.

因为∠ABD=∠ACD=90°，∠BAD=∠CAD=30°，所以AD=2BD=2CD，从而获得AD=BD+CD. 又如，当D与B重合时，则AD=AB，BD+CD=BC，因为AB=BC，所以AD=BD+CD.

通过上述几个特殊位置的求解，学生很容易通过合情推理的方式获得BD，AD，CD之间的数量关系，即AD=BD+CD. 但上述结论是通过合情推理所获得的，其结论本身就具有或然性，因此，还需要通过演绎推理的方式进行证明.

值得一提的是，由于证明三条线段之间的数量关系比较困难，教师可以引导学生通过旋转或者截长补短的方式将其转化为两条线段之间的数量关系.

（2）△ABC是等腰直角三角形

如图3所示，∠BAC=90°，我们不妨选取D为弧BC的中点，显然此时四边形ABDC就是正方形.

显然，通过上述几个特殊位置，学生很容易通过合情推理获得BD，AD，CD之间的数量关系，即BD+CD=CD. 但上述结论是通过合情推理所获得的，其结论本身就具有或然性，因此，还需要通过演绎推理的方式进行证明.

（3）△ABC是顶角为120°的等腰三角形

如图4所示，∠BAC=120°，类比上述探究策略和方式，教师可以引导学生通过合情推理获得BD，AD，CD之间的数量关系，即BD+CD=AD.

2. 一般情况

经过上述特殊情况的探究，学生已经认识到了BD，AD，CD之间的数量关系与△ABC的形状有关，并且还将三条线段之间的关系转化成了两条线段之间的关系，即BD+CD与AD之间的关系. 此时，教师应及时引导学生通过如下转化的方式将其转化为一般情况.

如图5所示，延长DB到点E，使得BE=DC，然后连接AE.

显然，要获得BD，CD，AD之间的关系，就是需要添加等腰三角形ABC中底边长度与腰的长度之间的比值.

3. 问题拓展

学生通过观察、猜想、验证、证明等步骤发展了自己的推理能力，提高了自己发现问题、解决问题的能力，但上述逻辑推理过程是就题论题，在一定程度上还不利于学生的全面发展，因此，教师还应引导学生探究更为一般的拓展问题.

（1）动点D在等腰三角形ABC腰所对应的劣弧上

如图6所示，已知D为弧AB上的一动点，AB=AC，试求BD，CD，AD之间的关系.

（2）动点D为等腰三角形ABC外接圆上的任何一点

由于点D的位置不确定，所以就需要学生分类讨论，进而把问题转化为上述原题和拓展类题目. 值得说明的是，由于分类讨论的过程就是对问题共性的抽象过程，在此期间，学生多角度思考问题，其本身就是一种逻辑推理方式.

（3）从等腰三角形到特殊四边形

上述所研究的问题都是三角形，那么将三角形替换为四边形，则更有利于学生深度发展自己的逻辑推理能力.

如图7所示，已知圆外接于正方形ABCD，若P为圆上的任何一点，然后连接正方形ABCD的任何三个顶点，则探究这三条线段之间的关系.

总之，逻辑推理素养是学生在数学学习过程中逐步形成和发展的，因此，当学生在遇到一些较为复杂的问题时，教师应及时引导学生从一些特殊情况着手，不断获取数学思维活动经验，并以此问题为导向，通过变式问题的方式不断促使学生发现问题和提出命题，多角度探索论证思路，努力促使学生由理性思维走向理性精神，进而不断提高学生的逻辑推理素养[3].

参考文献：

[1] 肖冬. 在核心素养培养的背景下再思初中数学教学中逻辑思维能力的培养[J]. 数学教学通讯，2021（32）：45+48.

[2] 徐晓华. 基于逻辑推理素养下的高中数学立体几何教学策略探析——以“直线与平面垂直的判定”为例[J]. 数学教学通讯，2021（33）：43-44.

[3] 陈贇. 逻辑推理核心素养下初中数学教学策略与实践——以“三角形稳定性”为例[J]. 数学教学通讯，2021（20）：16-17.

作者简介：闵峰（1966—），本科学历，中学高级教师，从事初中数学教学工作.