一种超松弛原始对偶不动点算法及其应用
黄文丽, 唐玉超, 文 萌
(1. 南昌大学数学系,南昌 330031; 2. 西安工程大学理学院,西安 710048)
0 引言
信号和图像处理[1]、医学图像重建[2]和机器学习[3]等中的许多问题都可以归结为求解下列形式的优化问题


事实上,迭代序列(4)恢复了Micchelli 等人[14]提出的不动点邻近点算法(Fixed Point Algorithm Based on Proximity Operator, FP2O)。基于文献[14]的理论结果,可知由(4)式定义的迭代序列{xk}在有限维Hilbert 空间中收敛到如下优化问题的解


另一方面,Condat[24]提出并研究了如下更加一般的三个凸函数和的优化问题

其中f、φ和L同问题(1),h:H →(−∞,+∞]是正则下半连续凸函数。易见,当h(x)=0 时,问题(6)退化为(1)。为求解问题(6),Condat 提出了一种原始对偶分裂算法,并基于向前向后算子分裂算法框架,证明了所提算法的收敛性。在这里,我们给出当h(x)=0 时,Condat 所提出的原始对偶分裂算法格式


本文工作创新点归纳如下:
1) 建立求解优化问题(1)的不动点方程。通过构造合适的范数,证明该不动点方程中的算子是平均的。从而提出具有超松弛的原始对偶不动点算法;
2) 基于现有不动点结论,证明所提算法的收敛性。同时,我们分析算法的遍历收敛率,所得结果对于PDFP2O 算法是新的。进一步,在对目标函数较强假设条件下,证明所提算法的线性收敛率;
3) 通过将所提算法应用于图像复原模型,数值结果表明,当步长参数γ固定时,松弛参数{αk}越大,算法收敛越快。本文所提算法所需迭代次数少于ADMM 算法[21]、PDS 算法[24]和PDFP2O 迭代算法[7]。虽然在某些情形下,所提算法的迭代次数多于PDFP2O AM 算法[19],但后者需要假设图像边界条件是周期的,而所提算法适合于任何边界条件的图像复原问题,从而应用范围更广。
本文具体安排如下,在第1 节中,我们给出一些证明所提算法收敛性需要的定义和引理。第2 节提出一种超松弛原始对偶不动点算法求解问题(1),同时分析和证明所提算法的收敛性和遍历收敛率,以及线性收敛率。第3 节将算法应用于求解全变分图像复原模型,以验证算法的有效性和优越性。最后,我们对全文进行小结。
1 预备知识
在本节中,我们将回顾一些基本定义和引理,这些可参见文献[35—36]等。设H是实Hilbert 空间,定义在H上的内积为〈·,·〉和范数为//·//。设L:H →G是非零有界线性算子,其中G是实Hilbert 空间。L∗:G →H表示L的伴随算子,满足〈y,Lx〉=〈L∗y,x〉, ∀x,y ∈H。
设A:H →2H是一集值算子,我们分别用graA={(x,u)∈H×H:u ∈Ax}和ranA={u ∈H:∃x ∈H,u ∈Ax}表示A的图和值域。算子A称为单调的,如果〈x −y,u −v〉 ≥0, ∀(x,u),(y,v)∈graA。A称为极大单调的,如果A是单调的且不存在单调算子B,使得B的图包含A的图。A称为τ-强单调的,τ>0,如果

下面,我们回顾非扩张等算子定义。
定义1[35]设C是H的一个非空子集,T:C →H,则:
1)T称为κ-Lipschitz 连续的,如果

特别κ=1 时,T称为非扩张的;κ ∈(0,1),T称为压缩的;
2)T称为σ-余强制的,σ>0,如果

特别当σ=1 时,T称为固定非扩张的;
3)T称为α-平均的,α ∈(0,1),如果存在非扩张算子S,使得

f的次微分∂f定义为

设f ∈Γ0(H), λ>0, λf的邻近算子定义为

则有如下结论成立:
1){xk}关于Fix(T)是Fej´er 单调的,即//xk+1−x∗//≤//xk −x∗//, ∀x∗∈Fix(T);
2){Txk −xk}强收敛于0;
3){xk}弱收敛于Fix(T)。
为建立本文算法的线性收敛率,我们将利用经典的Banach 压缩映射原理。
引理3(Banach 压缩映射原理)[35]设(X,d)是完备度量空间,设T:X →X是θ-Lipschitz 连续算子,其中θ ∈(0,1)。定义Picard 迭代序列如下:任取x0∈X,定义xk+1=Txk,则存在x∗∈X,使得以下结论成立:

和余弦等式

以及K是H上的一自伴随强正算子。
这两个结论在我们的证明中同样起着重要的作用。
2 超松弛原始对偶不动点算法收敛性和收敛率分析
为了求解问题(1),我们首先给出超松弛原始对偶不动点算法的算法格式如下。
算法1 超松弛原始对偶不动点算法(Or PDFP2O)

Require: 任取x0 ∈H, v0 ∈G,选取λ ∈(0, 1//L//2),γ ∈(0,2β),以及αk ∈[0, 4β−γ 2β ]。当k =0,1,2,···,计算(i) ~vk+1 =prox λγ φ∗((I −λLL∗)vk+ λγ L(xk −γ∇f(xk)));(ii) ~xk+1 =xk −γ∇f(xk)−γL∗~vk+1.(iii) vk+1 =(1 −αk)vk+αk~vk+1;(iv) xk+1 =(1 −αk)xk+αk~xk+1.当满足给定终止条件时,停止;否则,继续。Ensure: xk+1, vk+1.
根据Moreau 恒等式,设f ∈Γ0(H),对任意λ>0 和x ∈H,有

我们可知算法1 中(i)等价于


以及算法1 中(ii)等价于

定义T2:G×H →H为

进一步,定义算子T:G×H →G×H为

引理4 设λ> 0, γ> 0,若(v∗,x∗)是算子T的不动点,则x∗是问题(1)的解。反之,若x∗是问题(1)的解,则存在v∗∈G,使得(v∗,x∗)是T的不动点。
证明 由T的定义知,若(v∗,x∗)是T的不动点,那么有

根据(13)式和(14)式,我们可得
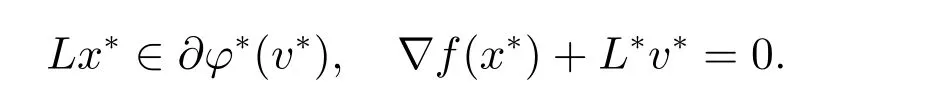
于是,我们有

即x∗满足问题(1)的一阶优化条件,从而是该问题的解。
反过来,若x∗是问题(1)的解,由一阶优化条件,我们有

根据(20)式,有v∗=T1(v∗,x∗),进一步用T1(v∗,x∗)替代(18)式中v∗,则有x∗=T2(v∗,x∗),从而(v∗,x∗)是T的不动点。
2.1 收敛性分析
下面,我们通过在G×H空间中定义合适的范数,证明由(12)式定义的算子T不仅是非扩张的,并且是一个平均算子。为了表达简洁,我们引进和定义一些符号,记


根据(12)式,并结合(24)式和(25)式,可得

又

其中(28)式中第一个不等式由∇f是β-余强制算子得到,第二个不等式由Young 不等式得到。将(28)式代入(27)式,我们有

下面,我们证明算法1 的收敛性。

设序列{vk}和{xk}由算法1 生成,(v∗,x∗)∈Fix(T),则有下列结论成立:

证明 根据算子T的定义,我们可知由算法1 定义的迭代序列{vk}和{xk}等价于

从而,根据引理2,我们可得结论1)∼3)成立。
2.2 收敛率分析
在本小节中,我们将分析算法1 的遍历收敛率和线性收敛率。首先我们证明遍历收敛率。为此,我们给出优化问题(1)的鞍点问题形式如下


由G(x,v)关于x的凸性和v的凹性,并结合Jensen 不等式,即得(34)式。

自然地

那么(34)式成立。


由(39)式,我们可得

根据Young 不等式,我们有

将(41)式代入(40)式,可得

(42)式中第二个不等号由∇f是β-余强制的推得,第三个不等号由条件(A1)和(A2)推得。因此

根据定理3 的结论,显然有ρ< 1,也就是说算子T是压缩的。下面,我们给出算法1 的线性收敛率结果。

3 数值实验
在本节中,我们应用所提出的算法1 求解经典的L2+TV图像复原模型
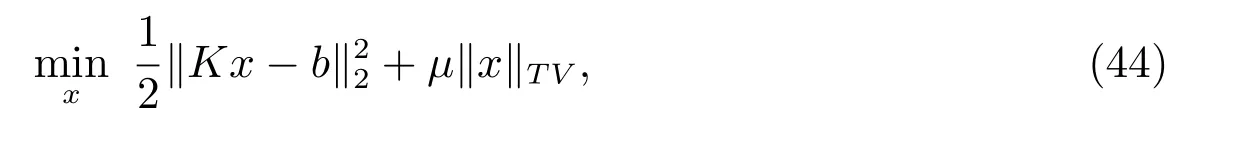
其中K ∈Rm×n表示模糊核矩阵,b ∈Rm×n表示观测图像,µ> 0 表示正则参数,以及//x//T V表示全变分。注意到全变分//x//T V可以表示为一凸函数φ和差分矩阵L复合的形式,即//x//T V=φ(Lx),详细可参见文献[14,38]等。从而模型(44)是问题(1)的特殊情形。
本节所有的实验是在联想笔记本E4430 完成的,其中CPU 2.3GHZ 和内存4GB。实验编程软件为Matlab R2014a。我们应用Matlab 函数fspecial 和imfilter 生成模糊图像,具体定义如下
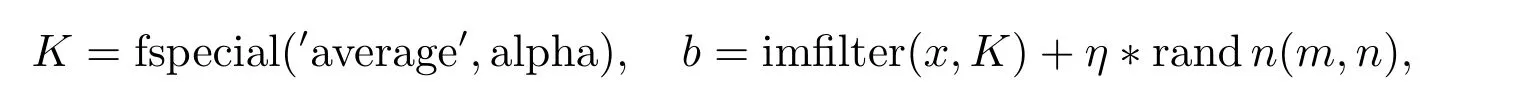
其中η表示加入高斯噪声的标准差,alpha 表示平均核的大小,x表示原始图像,以及b表示观测图像,实验测试图像见图1。

图1 测试图像
实验1 在实验1 中,我们说明松弛参数对算法1 收敛速度的影响。对比原始PDFP2O算法2,本文提出的算法1 提供了更大的松弛参数选择范围。特别地,算法1 允许松弛参数大于1。因此,在接下来的实验中,我们通过固定步长参数γ,根据松弛参数αk的取值范围,选择不同αk,报告所得数值结果,详细参数选取规则见表1。

表1 算法1 中步长参数γ 和松弛参数αk 的选取
根据文献[14],对于全变分一阶差分矩阵L,知//L//2≈8,因此,我们取λ=。此外,在本实验中β=1。我们选取图1中的文本图像作为测试图像。在实验中,我们取平均核的大小α= 3 以及η= 0.01。我们选取正则参数µ= 0.001。为评估复原图像的质量,我们选择信噪比(SNR)作为评价指标,其定义如下

这里x和xr分别表示原始图像和恢复所得图像。同时,我们给定算法的迭代停止准则为

这里ε是一给定正数,所得数值结果见表2。

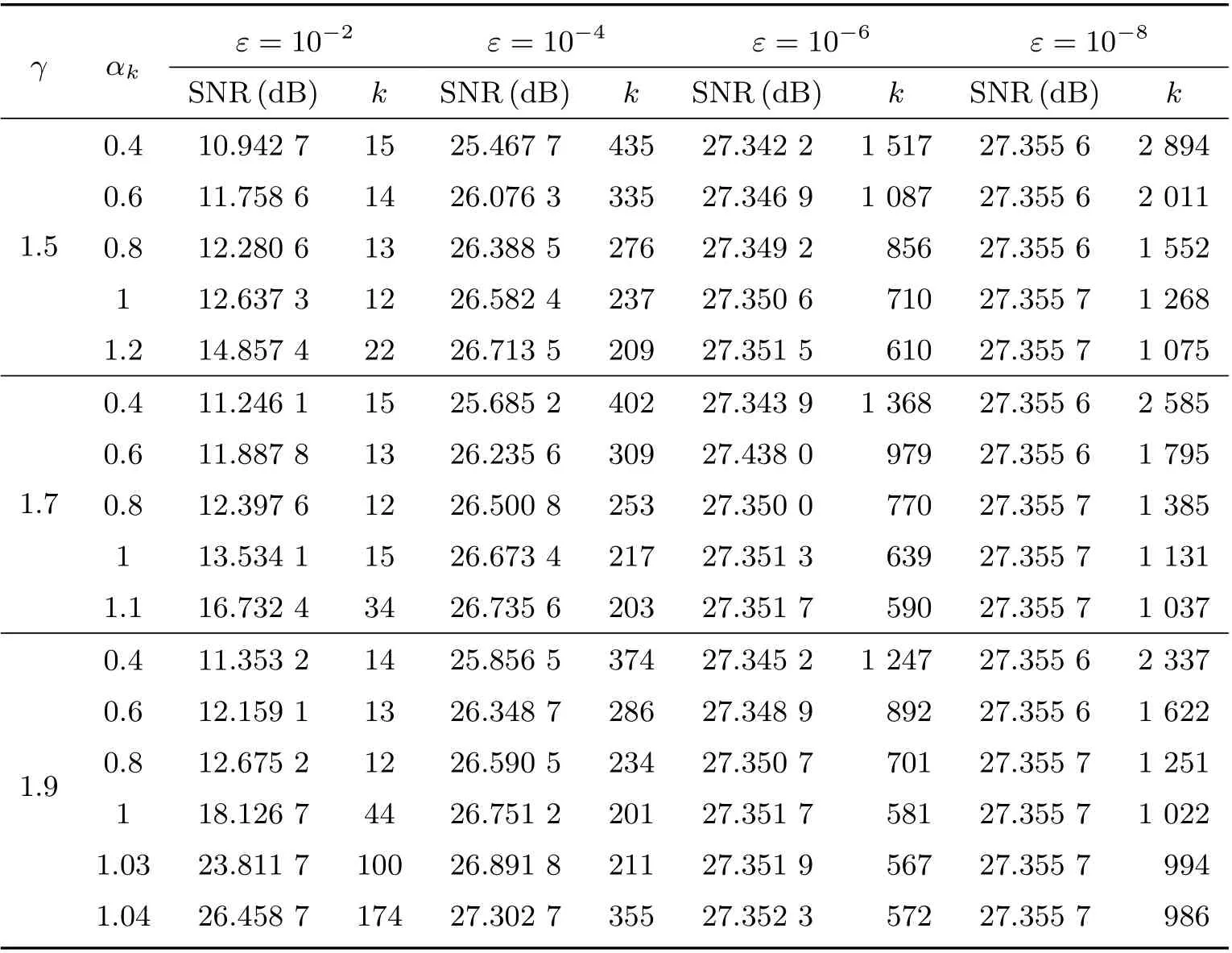
表2 不同步长参数γ 和松弛参数αk 的数值结果
续表
从表2 可以看出,当步长参数γ固定,松弛参数越大,算法收敛越快。当γ取值较保守时(γ ≤1),松弛参数αk> 1(超松弛情形)显然比松弛参数αk< 1 算法收敛更快。当γ接近理论上界时,随着求解精度的增高,超松弛参数算法所需迭代次数少于松弛参数αk=1 的情形。因此,在接下来的实验中,我们选取γ=1.9 和αk=1.04。
实验2 在实验2 中,我们比较所提迭代算法1 与现有其他算法,包括ADMM 算法[21]、PDS 算法[24]、PDFP2O 算法[7]和PDFP2O AM 算法[19]。我们选取图1 中的四幅图像作为测试图像,我们取两种不同大小的平均核分别是α= 3 和α= 7,并对每幅相应图像分别添加均值为零,标准差为0.01 和0.05 的高斯噪声。我们假定边界条件为周期边界条件,这时,对于ADMM 算法和PDFP2O AM 算法中矩阵的逆,可以通过快速Fourier 变换计算。我们调整正则参数µ以期达到最佳的图像复原结果,相应正则参数选取规则见表3。除了信噪比(SNR)以外,我们使用结构相似性指数(SSIM)[39]来评估恢复图像质量,SSIM 具体定义如下

表3 不同噪声水平下,最佳正则参数µ的选取规则

其中µx和µxr分别表示原始图像和恢复所得图像的平均灰度值,σx和σxr表示的是两幅图像的标准差,C1和C2为给定的非零常数。所得数值结果见表4 和表5。
从表4 和表5 可以看出,当ε=10−8时,分别取两种不同的平均核α=3, α=7 和噪声水平η= 0.01,对于风景和静物的测试图像,本文所提算法(算法1)比其他算法所需迭代次数更少。在其他情形下,算法1 仅次于PDFP2O AM 算法。由于PDFP2O AM 算法只在周期边界条件下才能执行,而本文所提算法与PDS 算法以及PDFP2O 算法可以适合于任何边界条件的图像复原问题,从而更具有广泛的应用性。为了更加直观观察恢复图像,图2 至图5 分别展示了当ε=10−8时,五种算法恢复所得图像。

表4 平均核α=3 时,比较不同迭代算法所得数值结果
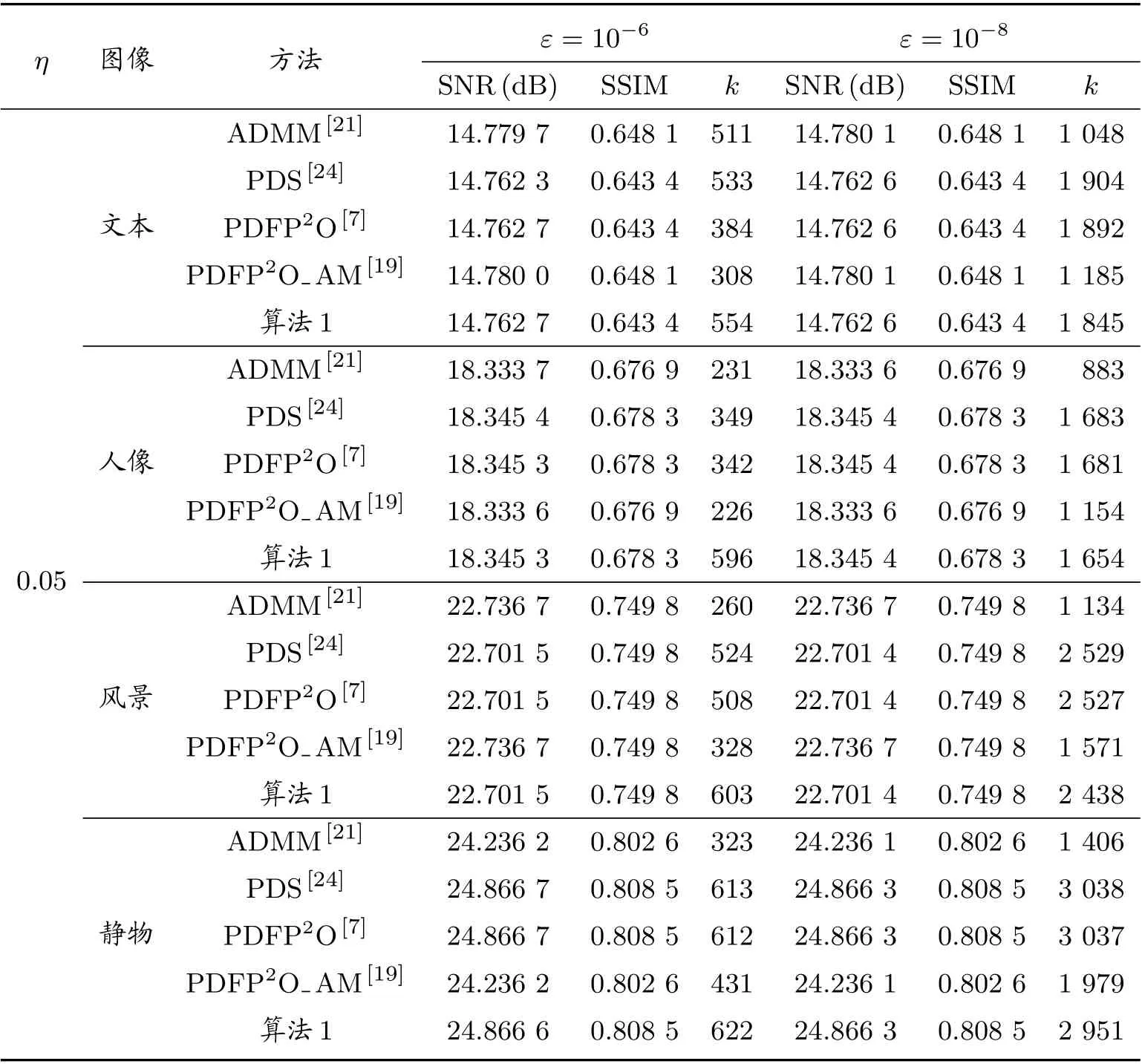
续表
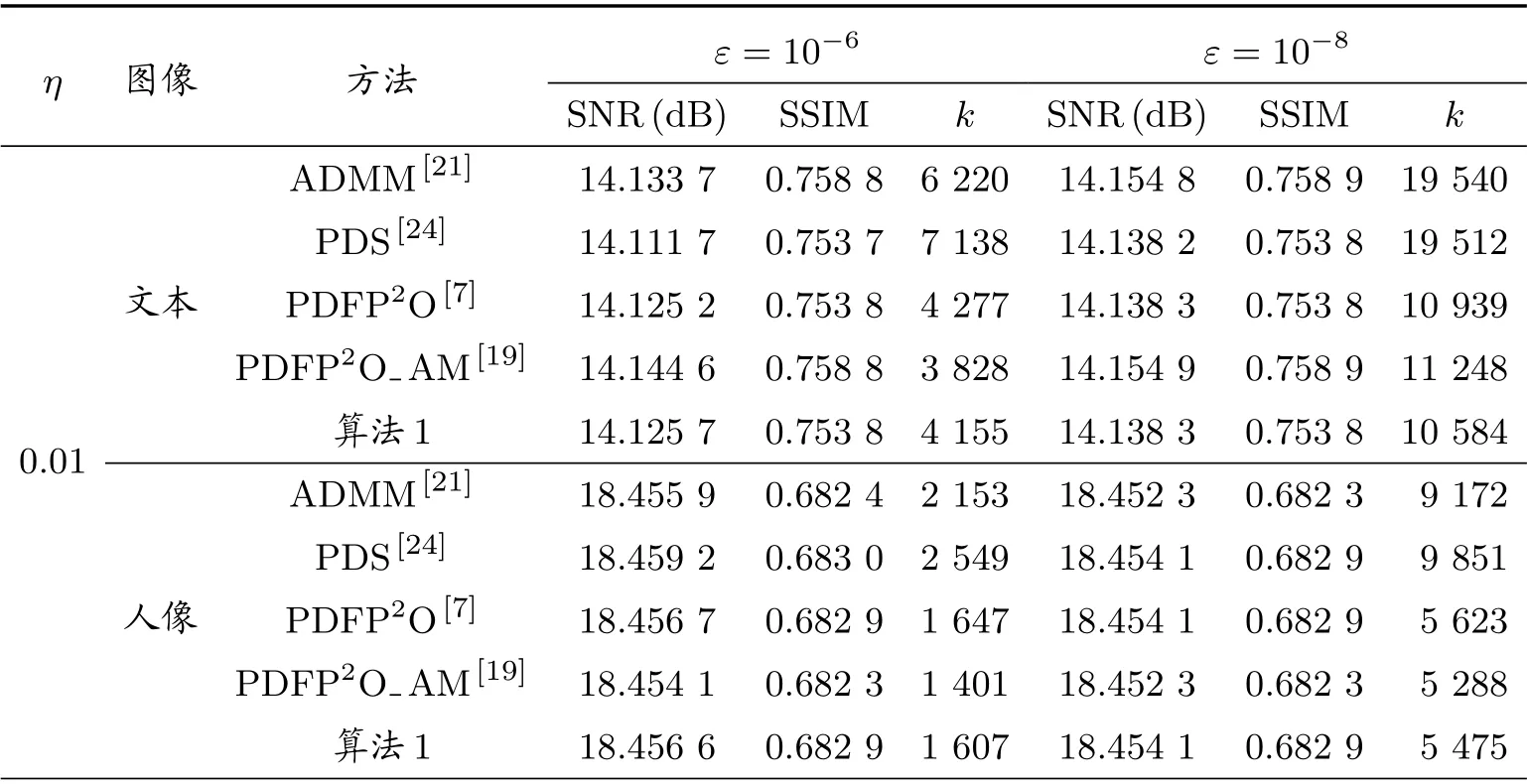
表5 平均核α=7 时,比较不同迭代算法所得数值结果
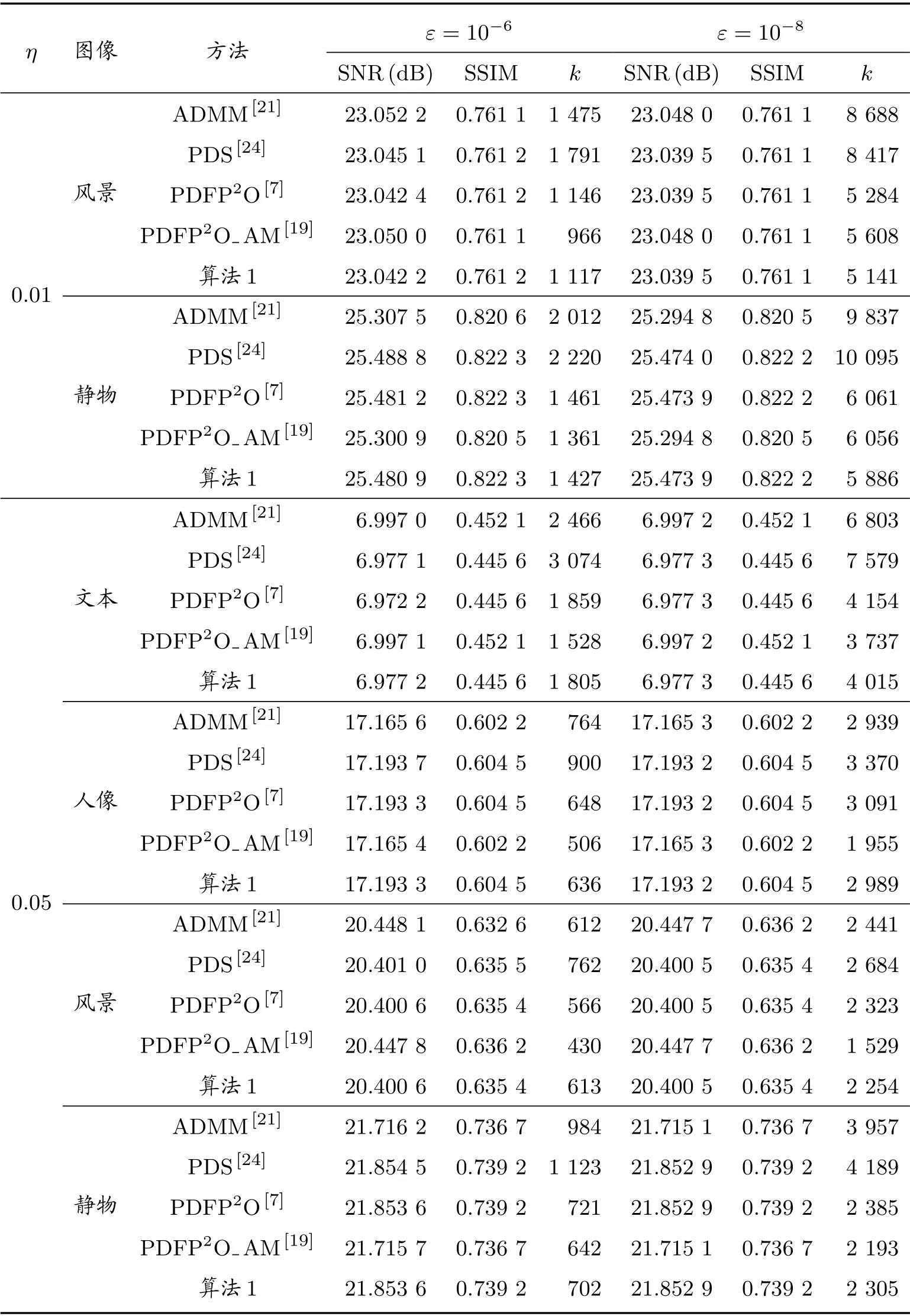
续表
图2 至图5 中的第一行是模糊和噪声图像;第二行是由ADMM 恢复的图像;第三行是由PDS 恢复的图像;第四行是由PDFP2O 恢复的图像;第五行是由PDFP2O AM 恢复的图像;第六行是由算法1 恢复的图像。

图2 模糊和噪声图像(文本)

图5 模糊和噪声图像(静物)

图3 模糊和噪声图像(人像)

图4 模糊和噪声图像(风景)
4 结论
本文提出了一种超松弛原始对偶不动点算法求解两个凸函数和的优化问题(1)。相比于现有的原始对偶不动点算法(2),本文的算法允许松弛参数大于1,从而扩大了原算法的松弛参数的选择范围。通过构造合适的范数,基于不动点理论,我们证明了所提算法的收敛性,同时证明了算法的遍历收敛率。进一步,在对目标函数较强假设条件下,我们证明了算法的线性收敛率。为验证算法的有效性和优越性,我们应用于求解全变分图像复原模型(44),数值实验结果表明,超松弛参数算法优于松弛参数小于等于1 的情形。
无论是PDFP2O 算法,还是本文提出的超松弛PDFP2O 算法(算法1),算法的步长参数依赖于目标函数梯度的Lipschitz 常数,当该常数未知时,只能凭经验选取步长。因此如何克服这个不足,使得算法更加方便执行,这将是我们接下来研究的问题。

