带消失位势的p-Laplace型拟线性薛定谔方程的正解

王亚男, 滕凯民

(太原理工大学数学学院, 山西晋中 030600)

1.引言

本文考虑如下p-Laplace型拟线性薛定谔方程正解的存在性

当κ < 0时, 在文[4]中, Poppenberge等人通过约束极小化方法, 考虑了方程(1.3)正解的存在性.之后, LIU等人[5]通过变量代换将拟线性问题转化为半线性问题, 并以Orlicz-Sobolev空间框架作为工作空间,利用山路定理证明了方程(1.3)正解的存在性.同时Colin和Jeanjean[6]采用对偶方法, 选取Sobolev空间H1(RN)作为工作空间, 利用山路定理研究了方程(1.3)正解的存在性.LIU等人在文[7]中引入新的扰动方法, 研究了一类次临界拟线性问题, 并在文[8]中证明了临界情况下解的存在性.此外, 利用Nehari流形, LIU等人在文[9]中研究了基态解的存在性.

当κ>0时, Alves等人在文[10]中考虑了非线性项

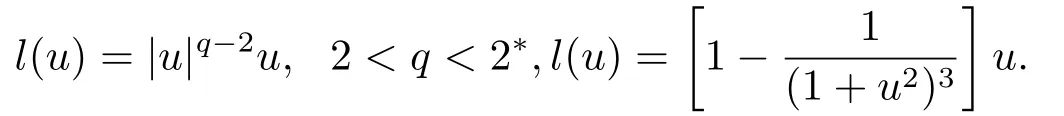
其中V 和Q在原点处可以是奇异的, 无界的, 或在无穷远处消失的位势, 他们利用极大极小方法和L∞估计, 证明了该方程非负解和非零解的存在性.在文[16]中, Aires和Souto同样使用了文[10]中的变量代换, 研究了方程(1.3)非线性项是超线性情形.

然而, 对于消失位势的p-Laplace型拟线性薛定谔方程, 关于其正解的存在性研究的结果不多.本文的主要目的是, 利用山路定理研究方程(1.1)当κ > 0和位势V(x)在无穷远处消失时,其正解的存在性.

为了陈述主要结果, 我们假设V(x):RN→R满足如下条件:

2.准备工作

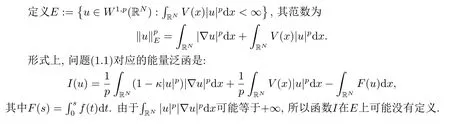
另一方面, 由于位势V(x)可能是局部的, 我们采用罚函数方法考虑如下辅助问题

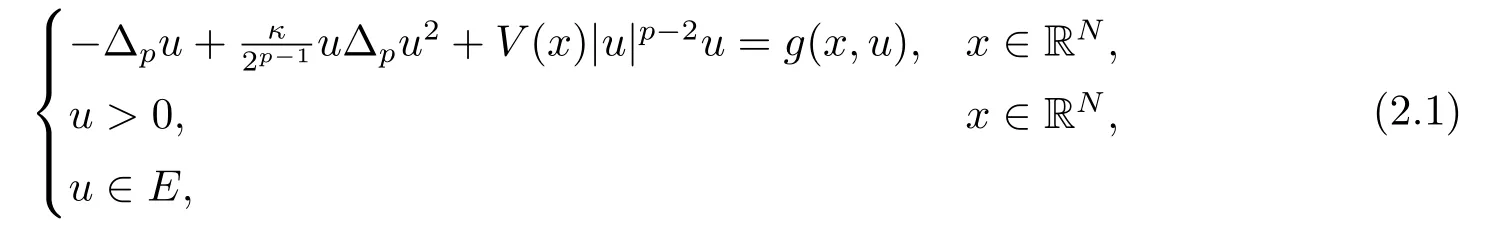
其相对应的形式能量泛函为:

证根据l的定义, 有

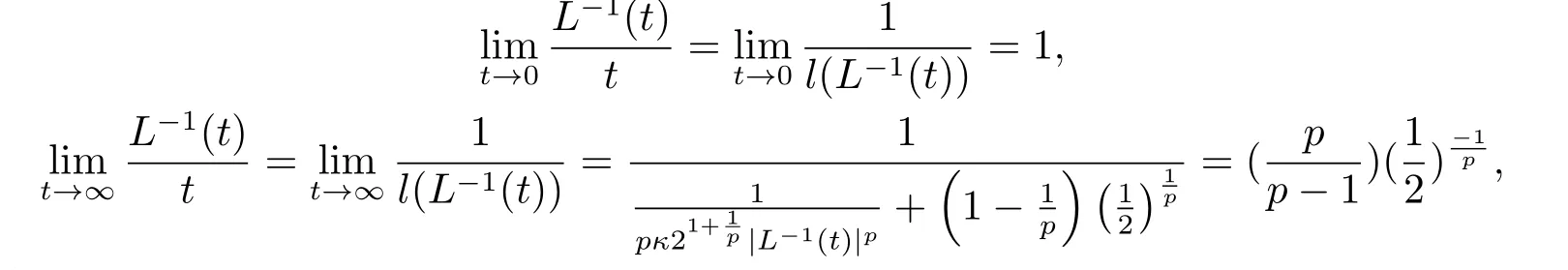
这就得到了(i)和(ii).

3.正解的存在性证明

J满足山路几何结构.

引理3.1假设(V1), (f1)-(f4)成立, 那么

(i)存在ρ,α>0, 使得J(v)≥α, 且∥v∥E=ρ;

(ii)存在e ∈E, 使得∥e∥E>ρ和J(e)<0.

证(i) 由引理2.2的(iii)和引理2.3的1)可得

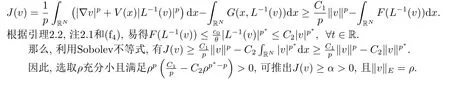
(ii) 根据(f4), 存在正常数C1,C2使得

根据引理2.2的(iv), 有

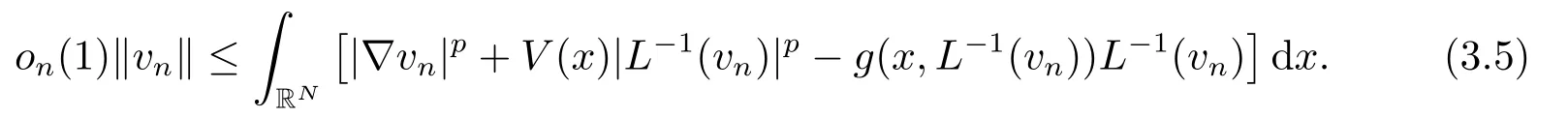
结合(3.2)和(3.5)式, 可推导出

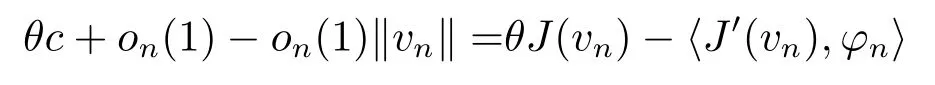
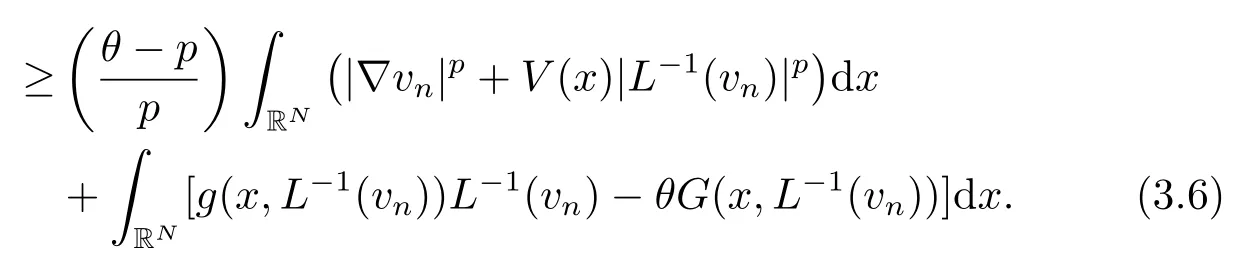
根据引理2.3的5)可得

因此v−= 0 a.e.在RN, 且v ≥0.由强极大值原理, 即知v > 0在RN.由此可得u = L−1(v)是方程(1.1)的正解.

引理3.4当R>1时, v ∈E是如下方程的一个弱解

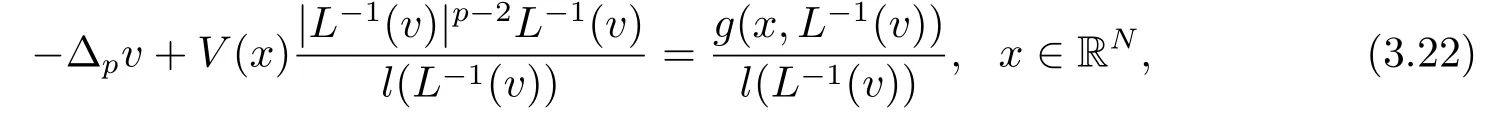
证由v是J的临界点, 可得

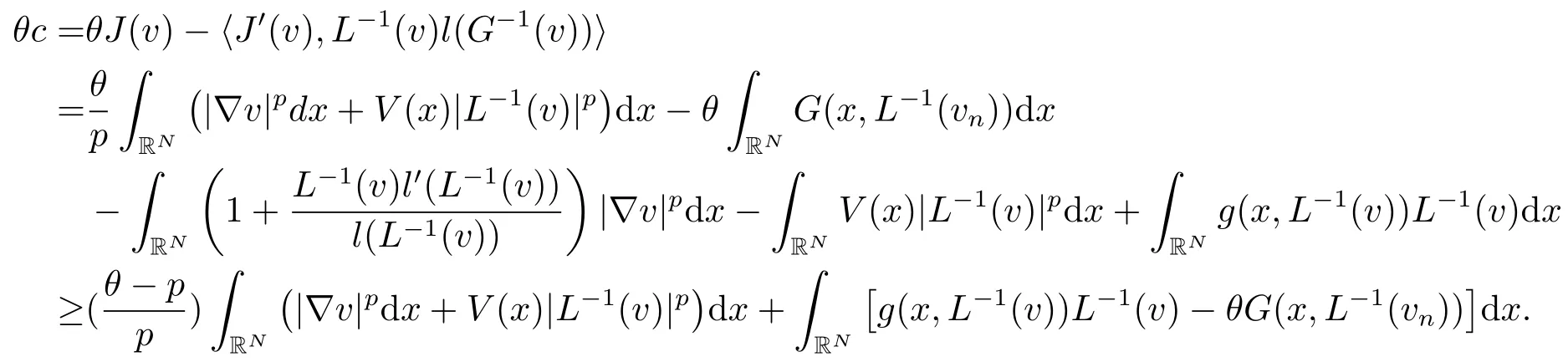
利用引理2.3的5), 有

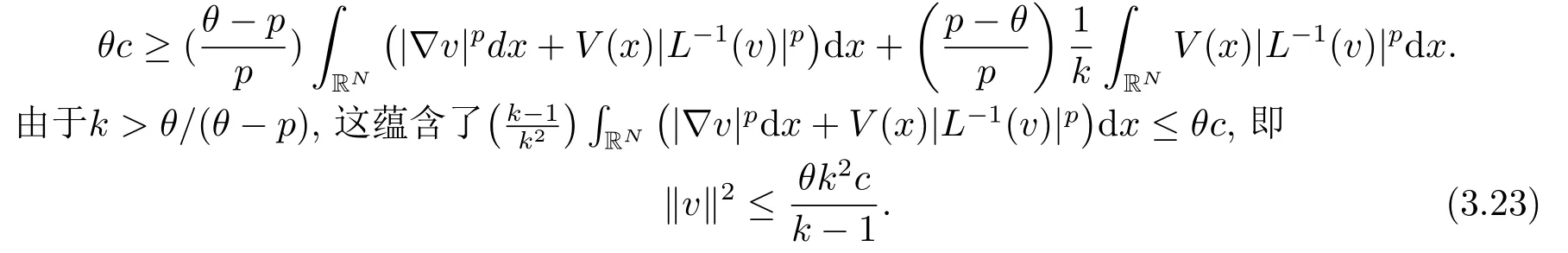
引理3.5存在M >0满足∥v∥∞≤M∥v∥p∗.

证对任意的m ∈N, β >1, 令Am={x ∈RN;|v|β−1≤m}, Bm=RNAm和

注意到vm∈E.通过计算∇vm, 可得

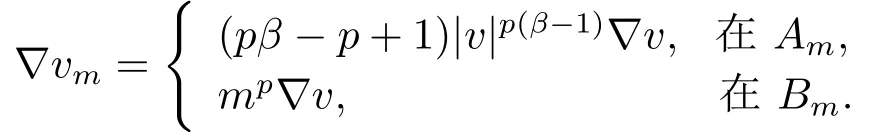
因此, 取vm为测试函数, 有

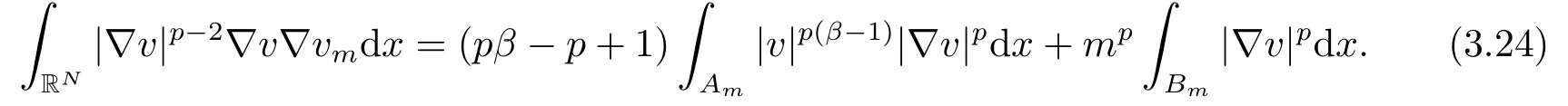
现在, 令

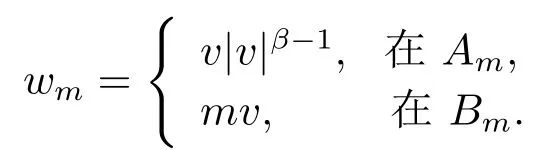
这蕴含了|wm|p=|v|p−1vm≤|v|pβ和

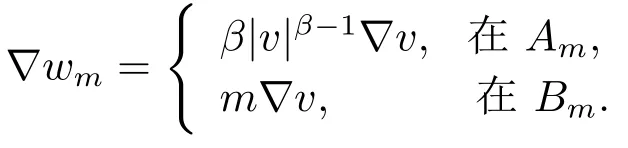
事实上

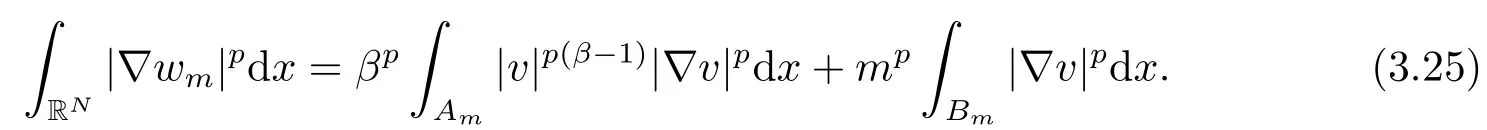
那么, 结合(3.24)和(3.25)式, 有

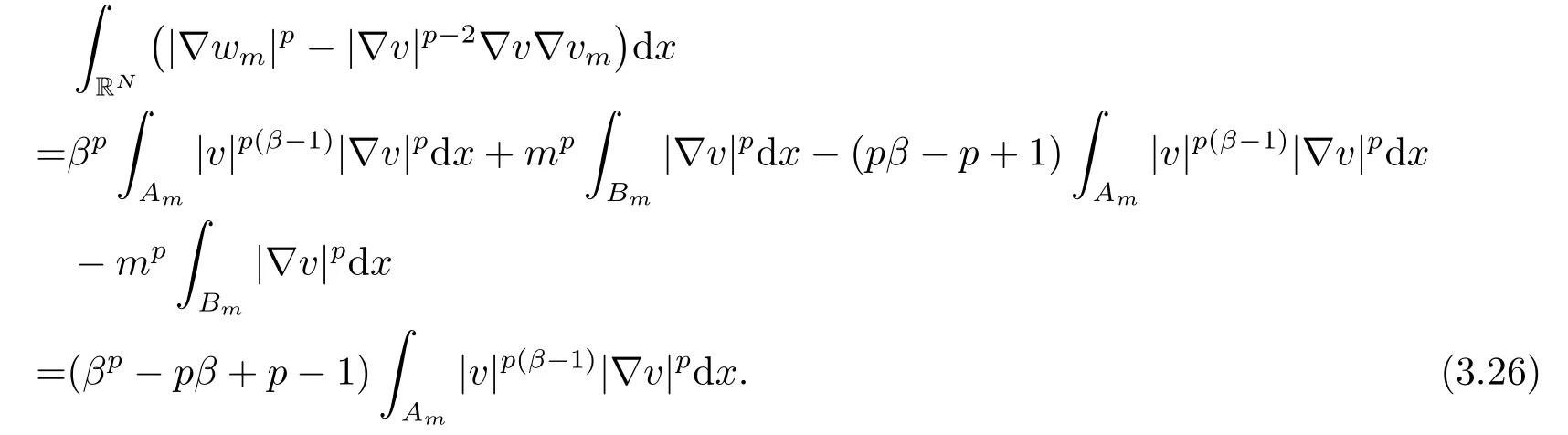
利用vm为测试函数, 可推出

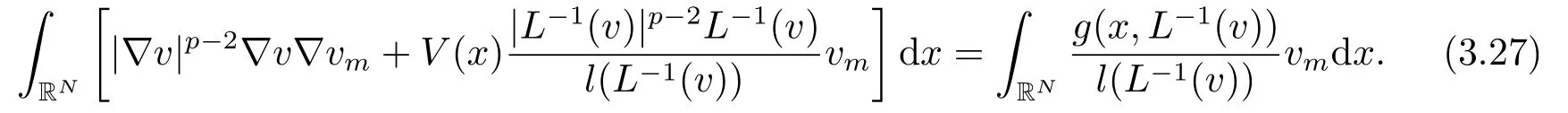
结合(3.24), (3.26)和(3.27)式, 易得

事实上, 当|x|=R时, v(x)≤u(x).选取测试函数

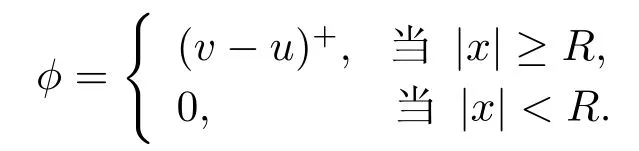
这蕴含了ϕ ∈E.由于v是方程(3.22)的一个解, 可推出

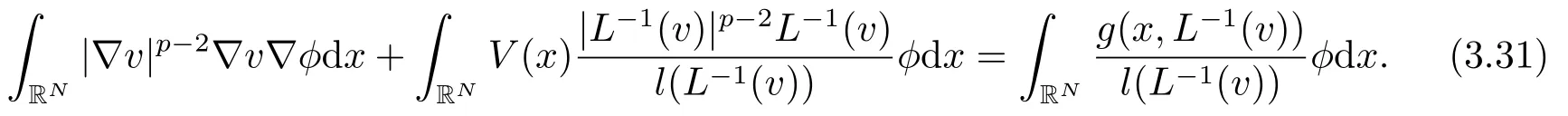
另一方面, 根据基本不等式(见文[18]中引理2.1):当p > 1时, 存在C(p) > 0, 使得对任意的η1,η2∈RN, 有

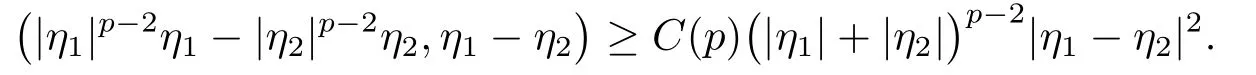
利用该不等式, 可得

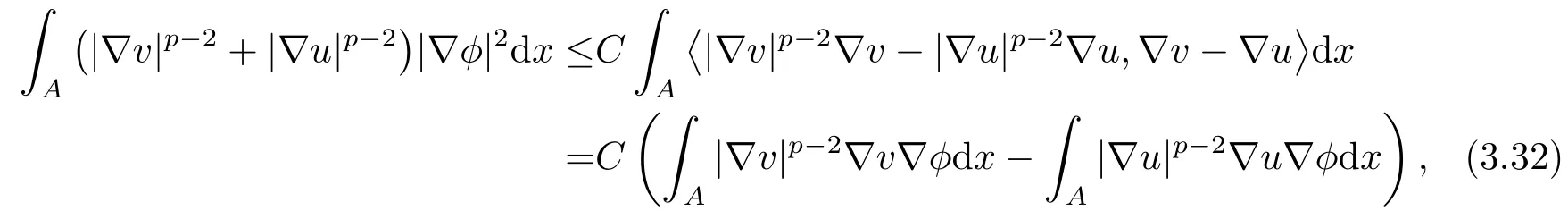
其中A={x ∈RN:|x|≥R和v(x)>u(x)}.