发展数学创新思维 培育数学核心素养①

黄秦安 张 静 曹新润

(1.陕西师范大学 710119；2. 西安市高新第一学校 710076)

培养知识创新型人才已经作为一项国家奠基工程被放在中国教育改革的突出位置，并获得了教育界的共识.从数学教育的角度看，数学创新思维及其培育应该成为数学核心素养教育的一项统领性和贯穿性的重要任务.数学创新思维作为数学核心素养的集中体现，综合性地展现了数学核心素养的基本要素，并且是衡量数学核心素养的重要指标.作为数学素养教育的一个重要内容，本文从讨论数学创造性思维的特征与结构入手，提出了数学创造力培育的对象是全体学生的基本理念，构建了数学创造性解决问题培育数学核心素养的样例，最后以数学审美为例表明培养创造性思维的途径与方式.

1 创造性思维的特征与数学创造性思维的结构

为了对数学创造性思维的特征予以探究，首先要从一般创造性思维的缘起谈起.在具有开创性的《创造性思维能力的因素分析研究》一文中，威尔逊和吉尔福德等学者首先提出了创造力测量的8个主要指标(特征)：对问题的敏感性；流畅性；灵活性；独创性；洞察力；分析力；综合力以及迁移力，以及每个指标所包括的具体内容.[1](见表1)

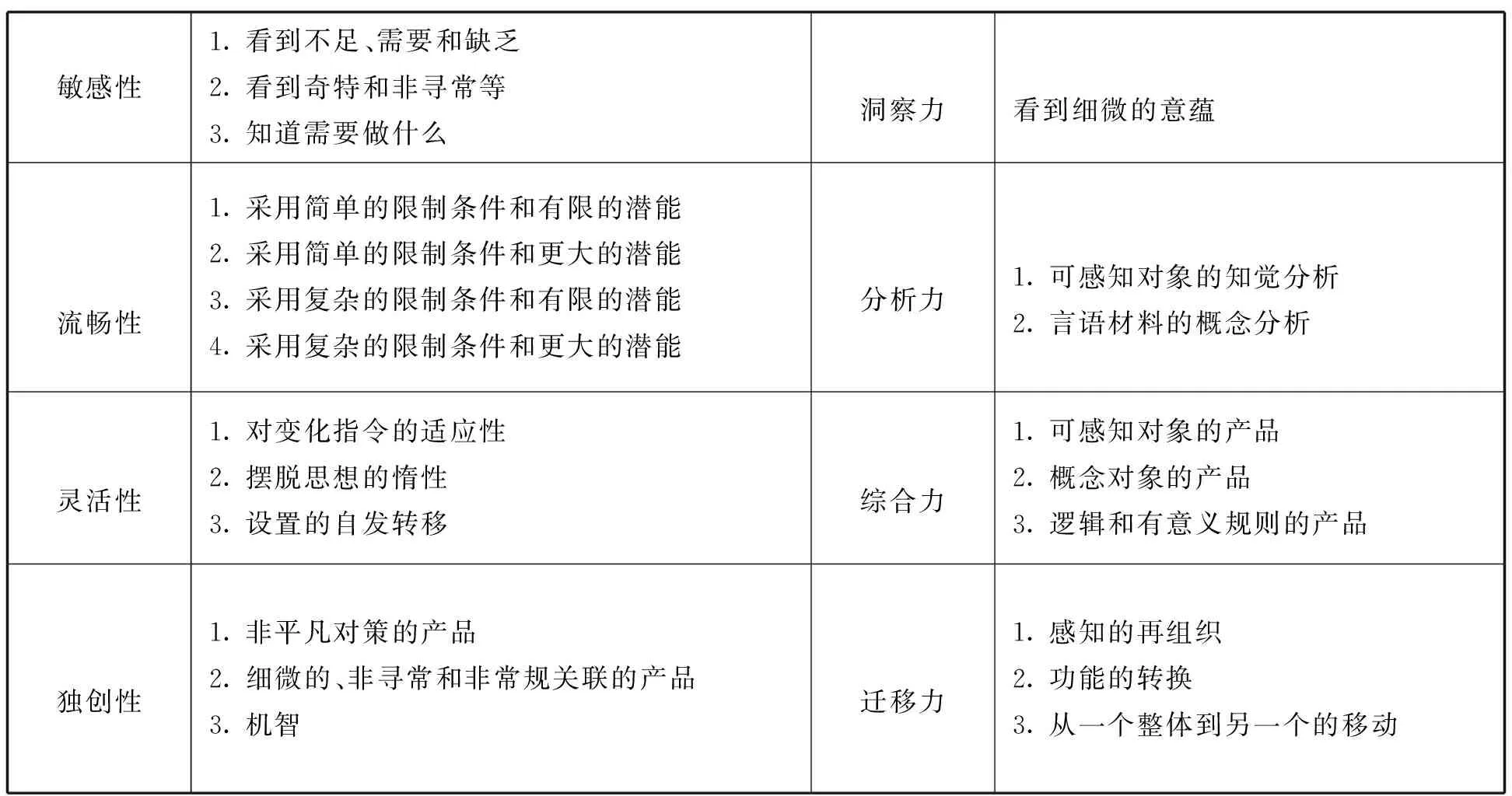
表1 威尔逊和吉尔福德创造力测量指标与细则

上述关于一般创造性思维指标、特征的描述同样也是适用于数学创造性思维的，只不过数学创造性思维除了上述特征之外，更具有其学科与知识的独特性.这种独特性具体体现在数学的知识特征和思维特征上.数学基本的思维类型可以看作是数学创造性思维的成分.包括逻辑、直觉、潜意识和想象.如果把发散思维和收敛思维结合在内，就构成了数学创造性思维的6个基本成分.

关于数学创造性过程的描述已有很多研究的成果，这里采用彭加莱和阿达玛关于数学创造的4阶段论.可以将其表述为：准备、尝试与探索、形成与完成、元认知评价.

我国著名数学家徐利治教授把创造能力定义为：创造能力=知识量×发散思维能力.[2]在这个公式中，徐老特别强调了发散思维在创造力中的分量.借鉴徐利治教授的研究成果，同时考虑到数学思维的成分与特征，我们把数学创造性思维的平面维度定义为数学创造性思维的基本成分(记为A)与数学创造性基本特征(记为B)的乘积，记为D=A×B.进而，把数学创造性思维的结构(记为G)定义为数学创造性思维的平面维度D与数学创造性阶段(过程，记为C)形成的体，即G=D×C= A×B×C.(图1)

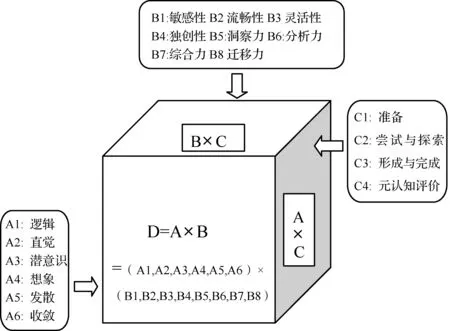
图1 数学创造性思维基本结构G= A×B×C

数学创造性思维的结构可以与某一标准的数学创造性思维层次相结合，形成特定历史时期、知识类别或难易程度不同的数学创造性思维的质性分析，并通过赋值分析加以定量研究.

2 在创造性思维发展中培育数学核心素养的典型样例

数学问题解决活动是培养数学创新思维的一个基本方式和教学平台.在数学课堂教学中，可以根据教学目标与教学内容，充分运用数学创造的逻辑，调动数学创新思维的基本要素，依据促进创造性思维的教学原则，建构数学问题解决的教学模式.在整个创造性解决问题过程中，教师所扮演的角色是指导者、咨询者,而不是包办者或代办者.教师要特别留意学生独特的、与众不同的解法，鼓励合作学习和研究性学习.在数学抽象、逻辑推理、数学建模、运算能力、直观想象和数据分析这6大核心素养中，每一类都可以通过上述模式开展创造性思维的培育.以下举其中的数学抽象、逻辑思维、运算能力为例加以说明.

第一，数学抽象.数学抽象就是采用数学的知识对研究对象进行概括和归纳的一种方法.数学抽象是数学知识的一个本质特征，也是数学思维的一种基本方式.

例1在哥尼斯堡，有一条河穿过城市，河上有两个小岛，有七座桥把两个岛与河岸连起来.(图2)来这里散步的大学生好奇地问了这样一个问题：能否从某个地点开始，不重复地一次走完这七座桥，最后回到起点.

过程分析：著名数学家欧拉听到这个有趣的问题后，通过数学抽象的方法，把河两岸的陆地和两个岛看成4个点，而将七座桥看作是7条直线，这样，哥尼斯堡7桥问题(图2)就被抽象成图3.于是，问题就变成了能否从图3中的某个点出发，一次走完所有的点而不重复.欧拉后来给出了相关问题(即一笔画问题)的定理，据此定理，哥尼斯堡7桥问题属于不可能问题.

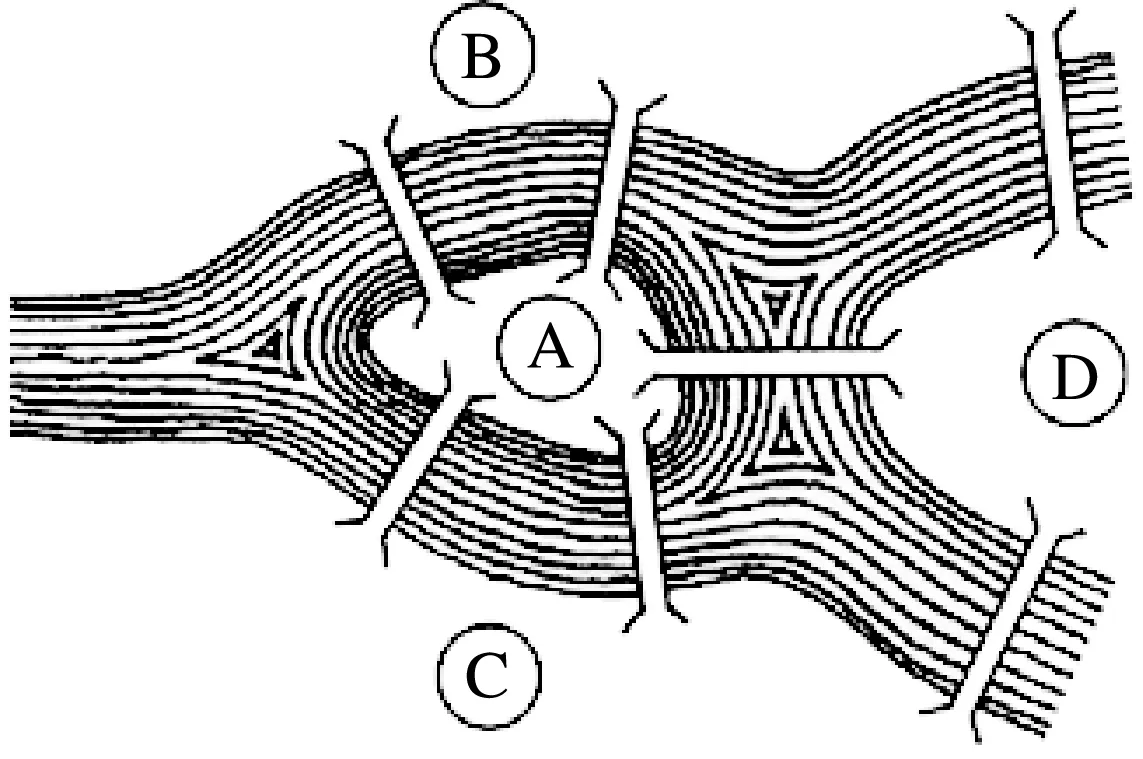
图2 哥尼斯堡7桥

图3 抽象图

正如哥尼斯堡7桥问题的成功获解那样，数学抽象包括一定程度的去情景化和去语境化.大数学家希尔伯特就曾主张：“数学实践要求人们发展一种能力，在没有完全摆脱语境的情况下，知道应该专注于什么是重要的.”[3]

第二，逻辑思维.逻辑思维是采用演绎推理进行的一种思维方式.比如数学中常用的反证法，就是建立在基本逻辑规律——排中律的基础之上的.

例2证明素数有无穷多个.

分析与解答：这个问题在古希腊欧几里得《几何原本》中就已得到解答.采用的就是反证法.假设素数只有有限多个P1，P2,…,Pn，那么构造P=P1P2…Pn+1，则无论P是一个素数，还是一个合数，都会推出矛盾.

有时候，正向思维的方向会有困难，逆向思维的恰当运用会有突破思维定势的创造.这时候可以从事物的对立关系中寻求解决之道.

例3n个人中，至少两人有相同生日的概率是多少？

分析与解答：对于许多问题，正面解决往往难度较大.本题目可以考虑“对立事件”：n个人有完全不同的生日的概率，就较容易解决.此题的方法体现了一种典型的“逆向思维”特征.而在事件的相互对立中寻求转换与统一，正是数学思维的精髓之一.因此，本题的答案为：

第三，运算能力.运算是一种最常见的数学方法.中国古代数学家刘徽和祖冲之对圆周率的计算精确度，达到了当时世界计算技术的巅峰.

例4刘徽对圆周率的计算.

过程分析：在割圆术中，刘徽在一尺为半径的圆内，作出圆内接正六边形，然后倍增边数，进而不断求出正十二边形、正二十四边形、正四十八边形、正九十六边形和正一百九十二边形的面积.在这一过程中，刘徽对运算能力的使用和把控达到了相当精确的高度.通过不断逼近的方法，求得圆周率为3.14(后人称之为徽率).

例5祖冲之对圆周率的计算.

过程分析：据《隋书·律历志》记载：“祖冲之更开密法，以圆径一亿为一丈，圆周盈数三丈一尺四寸一分五厘九毫二秒七忽，朒数三丈一尺四寸一分五厘九毫二秒六忽，正数在盈朒二限之间”.这就是说，祖冲之算出了圆周率数值的上下限：

3.1415926(朒数)<π<3.1415927(盈数).

数学史家推测，祖冲之是采用刘徽的割圆术，从正六边形一直算到正24576边形，才能得到圆周率的上述取值范围.[4]

更进一步看，数学运算能力不能简单地理解为程序性的计算步骤的完善性和计算过程的准确性，而是与数学课程改革中所倡导的数感紧密相关的一种能力，比如对数字的(超)直觉的一种感悟力和创造力.英国著名数学家哈代在《一个数学家的辩白》一书中曾举了2个相关的有趣例子.[5](见例6和例7)

例6在四位数中，只有8712和9801是其翻转数2178和1089的整数倍，即

8712=4×2178，9801=9×1089.

例7在1之后，只有4个数可以表示为其各位数字的立方和.这4个数分别是：

153=13+53+33，370=33+73+03，

371=33+73+13，407=43+03+73.

例8有一次，英国著名的数学家哈代乘坐出租车去看望住院的印度青年数学才俊拉马努金，哈代记得所乘坐的出租车号码是1729，就对拉马努金说这个数字看起来相当单调，而拉马努金则说：“不，它是一个非常有意思的数，它是最小的能用两种不同的方式表示成两个数立方之和的数”，即1729=123+13=103+93.这一发现看似偶然，却精妙无比.拉马努金的这种超级数感能力可谓大师级水准.要想达到这样一种境界自然不易，所谓冰冻三尺非一日之寒.但若从小处留意，从细微处做起，通过不断的数学文化积累(例如描绘数学家故事和成就的数学阅读、数学史上的典型事例)和长期不懈的数学解题欣赏和历练，最后达到一个较高的数感能力与数学直觉水平，对于每一个学数学的学生都是可以实现的目标.

3 让数学课堂的创造力培养模式常态化：数学美的视角

最后需要强调的是，在数学教学中，学生创造力和核心素养的培养，可以体现在任何教学环节和任何教学活动当中.在此，我们提出让数学创造力的培养常态化的口号.其基本含义是，创造性思维培养模式不仅仅是在问题解决活动中才可以使用，而是可以普遍地内化在日常的数学教学形态中，它应该成为日常数学教学不可或缺的一部分.进而，创造力作为核心素养最具本质特征的一个构成，就成为大众数学的重要培养目标，而不再限于精英教育的范畴.重要的是，只要教学活动是开放的、尝试性的、探索性的、鼓励猜想和推测的，只要主体是主动的、积极的、有想象力的和情感激越的，就给创造性思维提供了一个可以充分展示的教学空间.以下以“数学美感”为主题来对相关论点予以论证.

一般地看，数学美可以成为数学知识通往培育创造力的一个有力枢纽.惠特科姆(Allan Whitcombe)以数学中的算法教学为例，构造了一个算法、数学美与创造力的ABC模型[6](见图4).在这个模型中，B(数学美)成为从A(算法)到C(创造力)的一个必经之点.

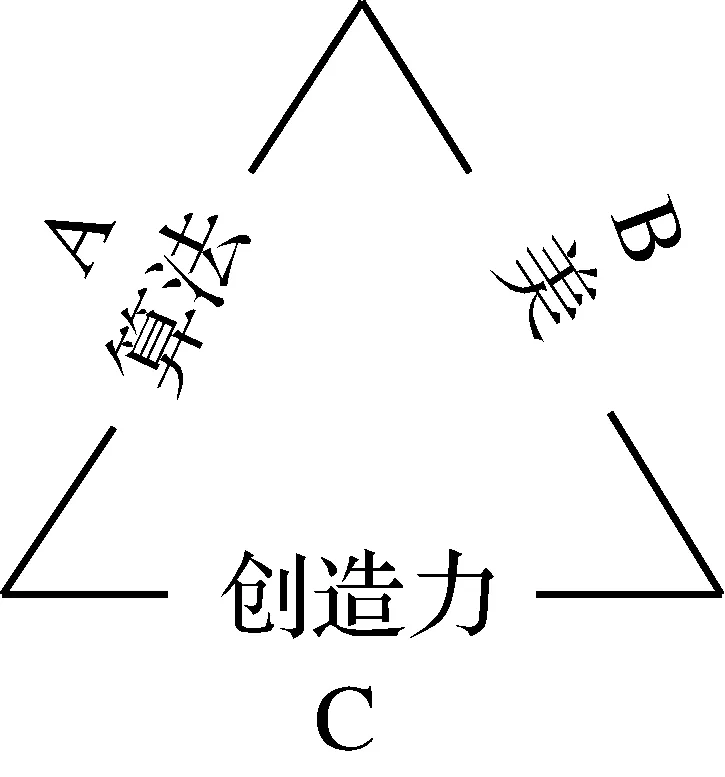
图4 ABC模型

具体地，惠特科姆例举了如下ABC模型下的详单序列.

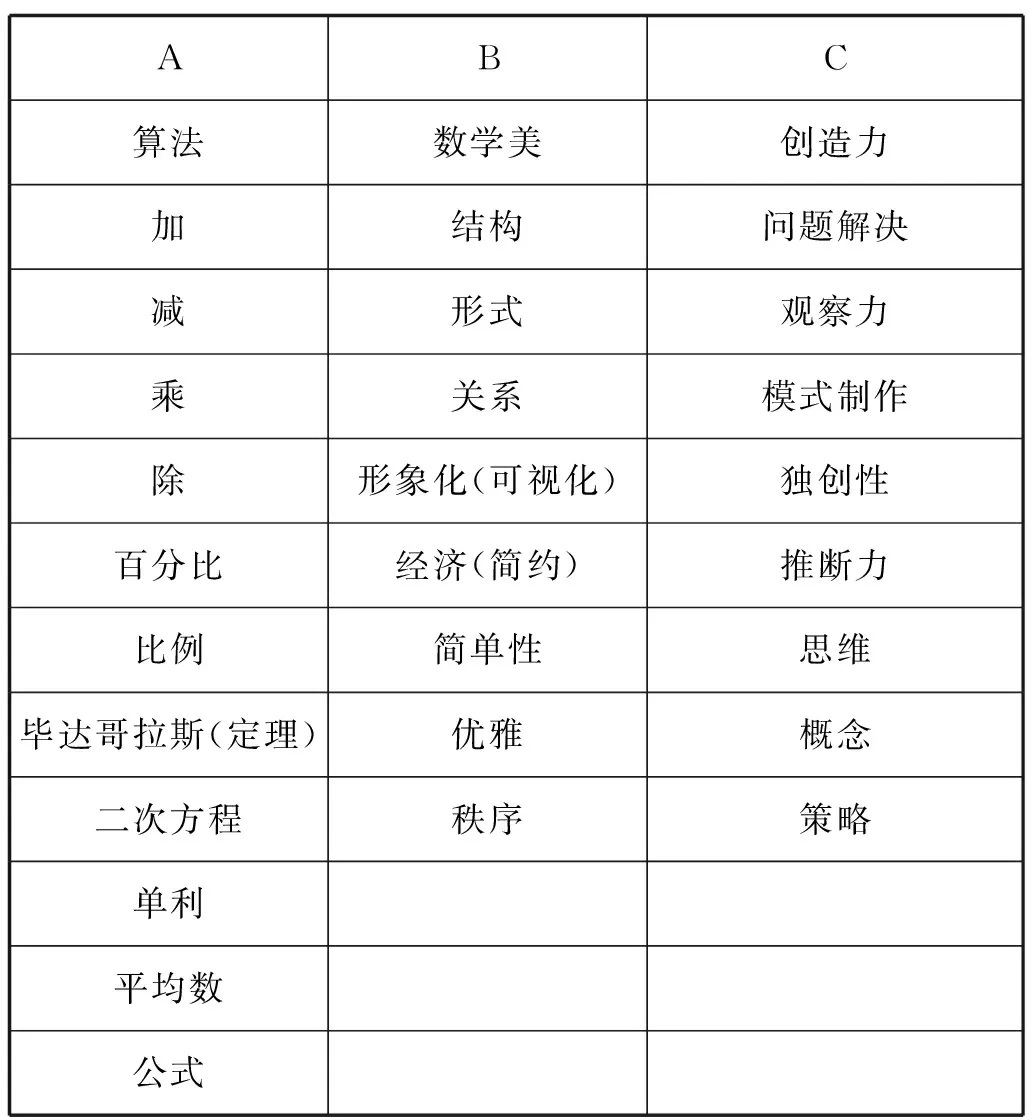
表2 ABC模型详单

惠特科姆写到：“除非我们激发学生的创造性思维，并使其延展到其想象力的极限，在某些情况下甚至超越极限，否则他们的数学之旅就会像泰坦尼克号一样，注定要失败的.”[6]以下通过几个典型例子，对如何在数学审美引导下激发创造活力，解决数学问题加以说明.

1)公式的协调优美性：许多数学公式本身就有一种美感，在推广和延宕的过程中，秉持这一原则常常会有令人惊喜的收获.

例9已知三角形的三条边长，求其面积，这就是著名的海伦公式

公式中a、b、c分别为边长，p为周长的一半.那么，可以把这个问题推广到四边形吗？

分析与解答：通过类比，从三角形的三条边到求四边形的四条边长，这时候需考虑增加一个条件，即四边形是内接于圆的，否则，面积就不能完全确定下来.大胆的联想是，是否四边形的面积仍然具有海伦公式那般整齐划一的美感.此时的妙处在于，根据美学的考量，d分别为四边长，p是周长的一半.果然，是成立的.到此，数学之妙与数学之美油然而生.

2)结构的完整之美：在不少数学问题中，题目条件与结论的关系仿佛是“犹抱琵琶半遮面”，需要进行结构的完整化，才能使之显露出“庐山真面目”.

例10如图，长方形ABCD中，AP=3，BP=6，CP=11，求DP=？(图5)

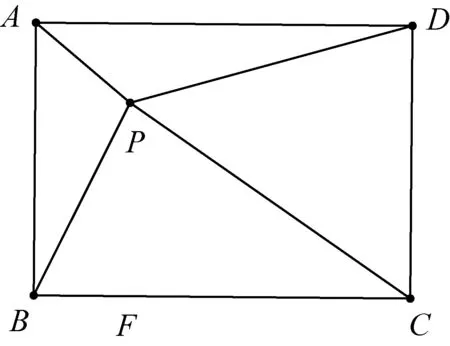
图5

分析与解答：根据美观性原则，矩形内一点到各个顶点的距离，一般需要借助于该点到各边的距离加以联系，因此，就容易想到一个具有“完美形式”的“关系图(图6)”.

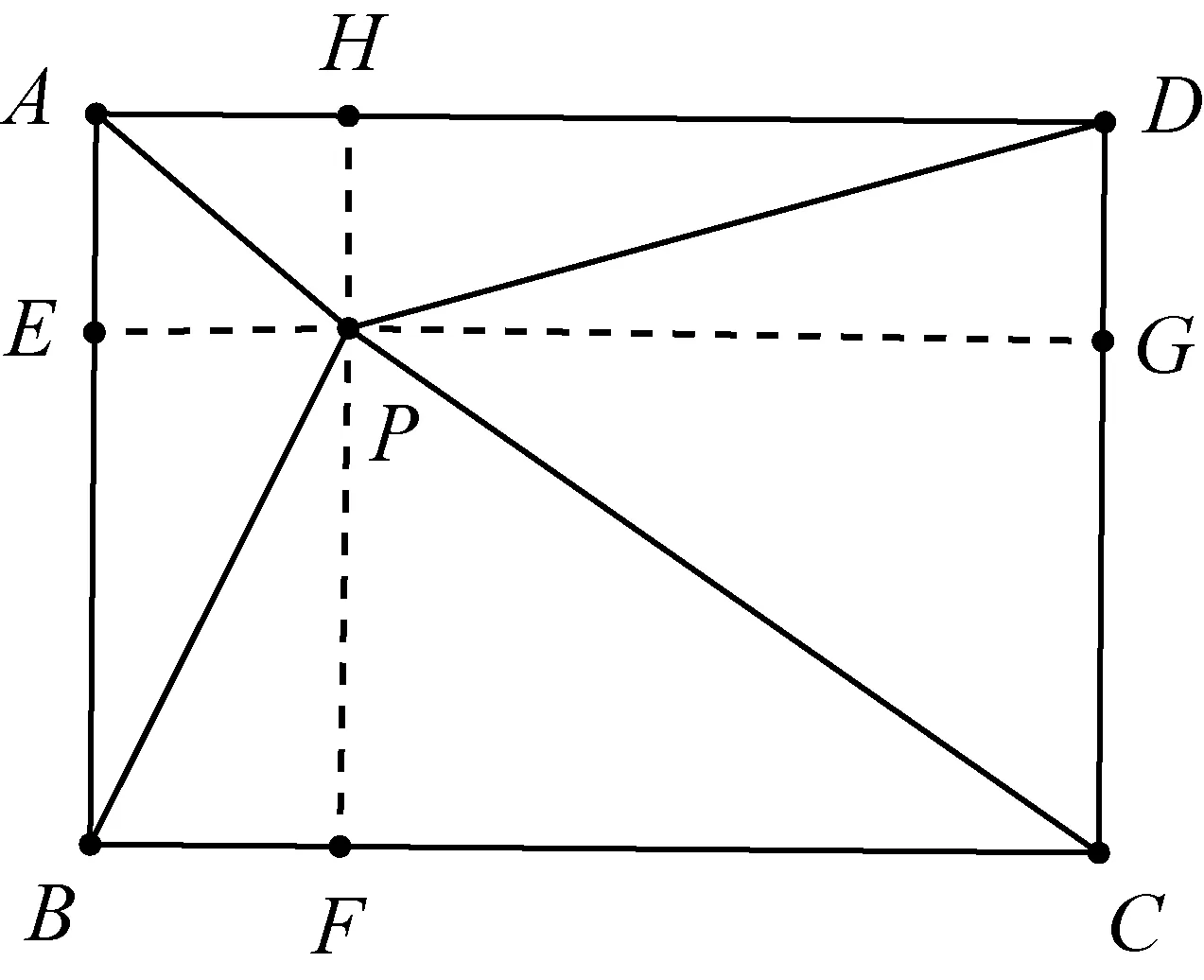
图6

根据图6的“完美图”，AP、BP和CP所关联的四段长度AE(DG)、BE(CG)、AH(BF)和CF(DH)，通过勾股定理得以联系起来.因此，

AP2+CP2=BP2+DP2.

3)维度的自如转换之美：从面到点与从点到面的联想转换空间.有时候可以先考虑一个问题的简单情形，然后再看简单情形下的结论是否在推广的情况下依然成立.

例11(如图7)在边长为a的正方形ABCD内，有一个边长为b的正方形EFGH，求证

图7

SABFE+SCDHG=SADHE+SBCGF

分析与解答：假如正方形EFGH缩成一点P(图8)，很明显的结论是

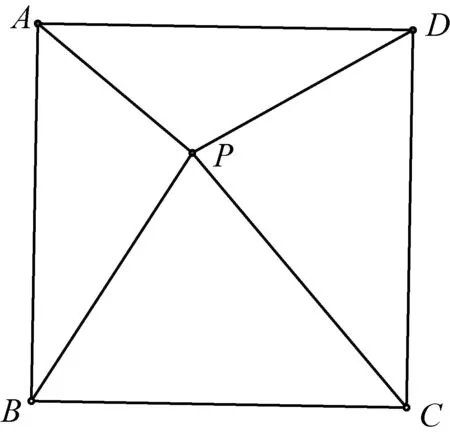
图8

如果把P点再换回成正方形EFGH.猜想应该是

SABFE+SCDHG=SADHE+SBCGF

成立.果然结果不谬(见图9).

图9

数学创造力与数学创造性思维作为数学核心素养的一个有机、重要且最具活力的组成部分，其培育和培养将在未来数学教育的改革中扮演越来越重要的作用.需要指出的是，数学创造力的培养绝不是少数学生的事，而是关系到所有学生和整个民族的文化素质的提高.其目标的达成与实现既要得到教育界和全社会的支持和参与，通过数学创造性思维的发展培育学生的数学核心素养，应该成为数学教育的一项艰巨和长期的任务，需要从教育思想、政策、课程、教材、师资培训和教法等方面进行全面、深入和持续的改革.