数学问题解答

2022年2月号问题解答

(解答由问题提供人给出)

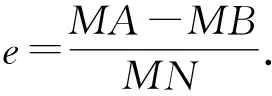
(河南辉县一中 贺基军 453600)

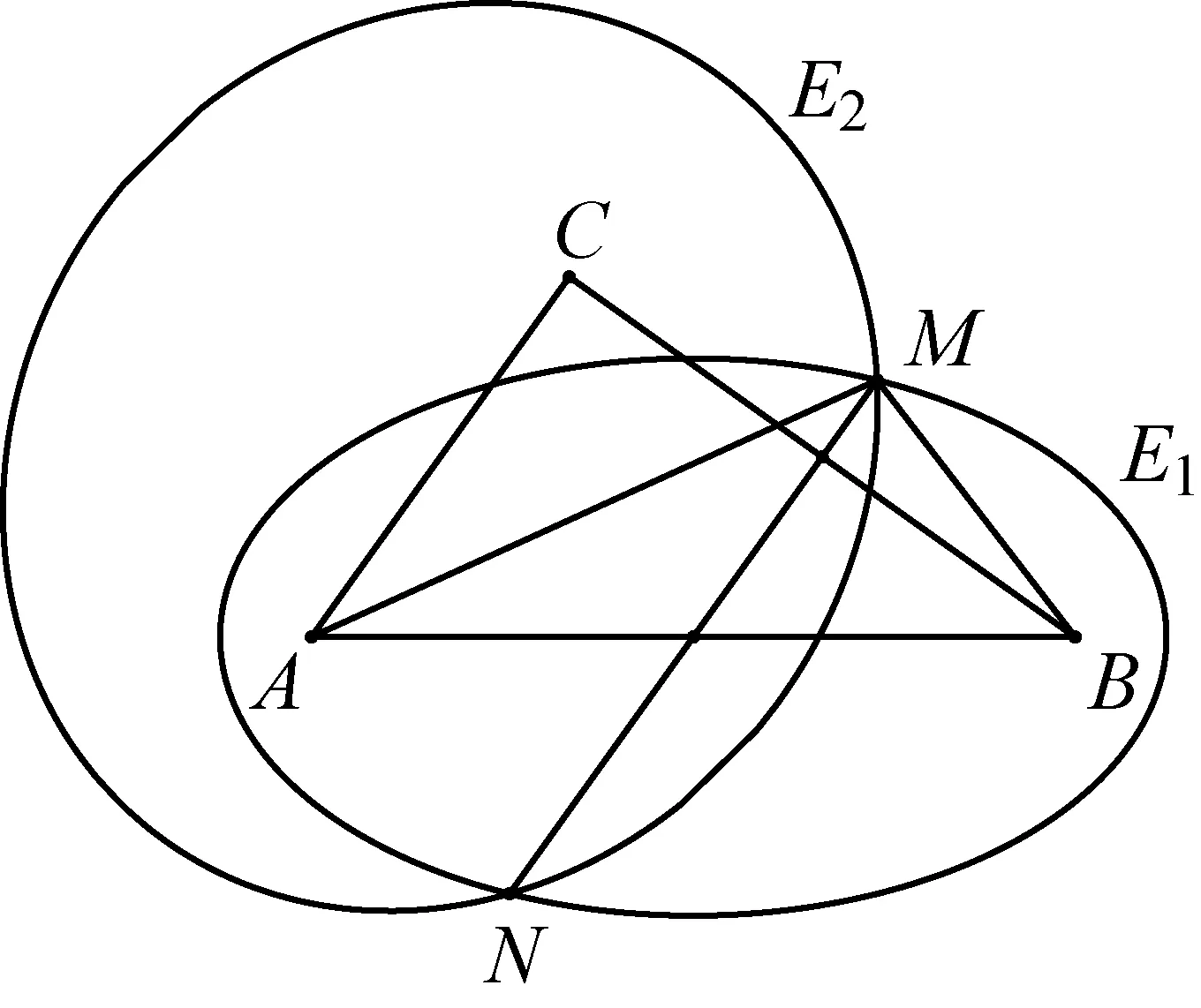
证明如图，直线MN与CB，AB分别交于点D，O，连接AN，BN，CN，CM.依题意，设椭圆E1与E2的长轴长都等于d.

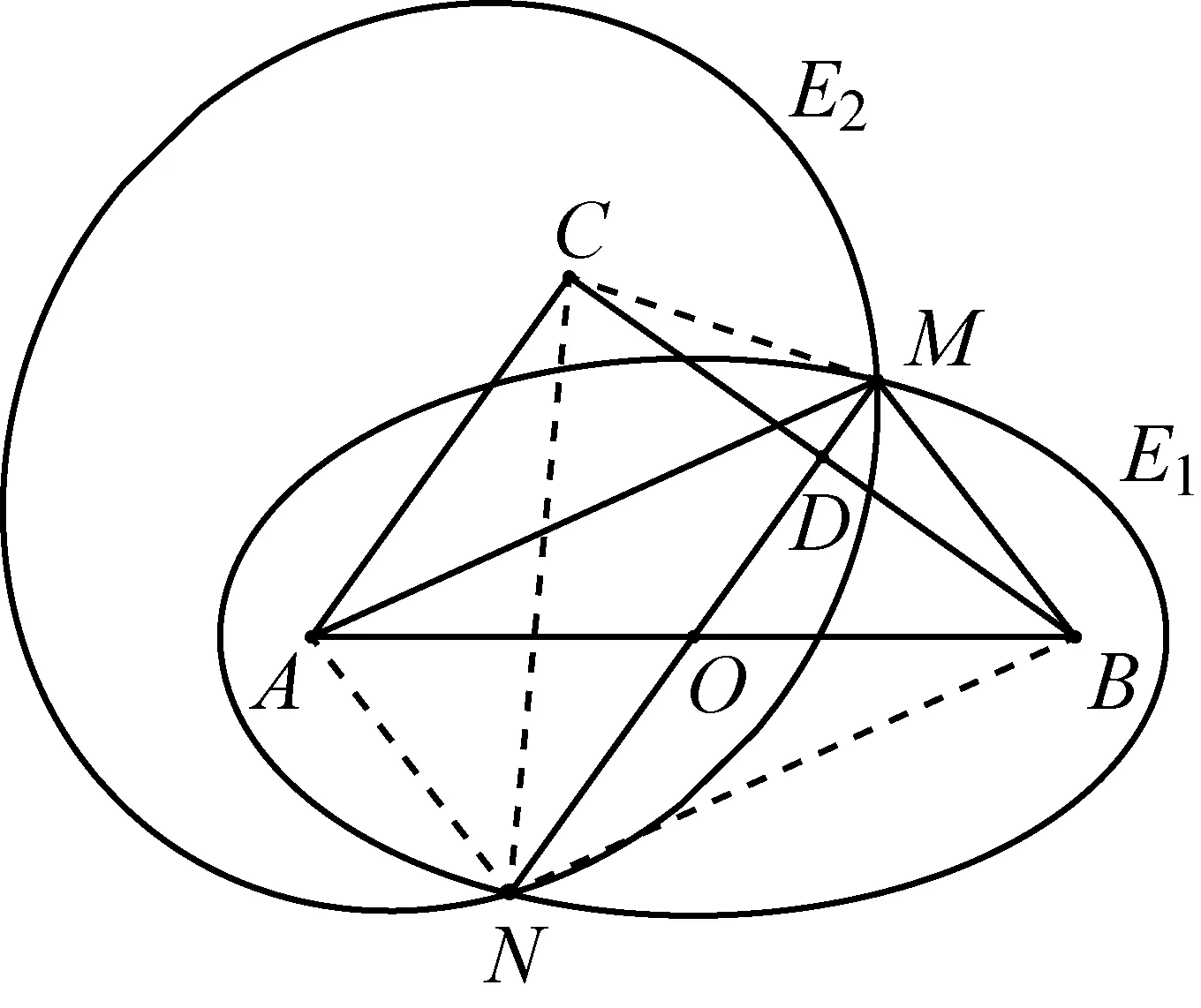
因M为椭圆E1与E2的交点，

故MA+MC=d=MA+MB，

从而得MC=MB，

同理得NC=NB，

因此直线MN为CB的中垂线，

且线段DO为Rt△ABC的中位线，

从而可知AO=BO，

其中点O为椭圆E1的中心.

因椭圆E1的弦MN过点O，故M，N两点关于点O对称，

从而可知MO=NO，

因此四边形AMBN为平行四边形.

综上，在四边形ACMN中，有

AN=BM=CM，AM=BN=CN，

同时有AC∥DO即AC∥MN，

因此，当AC=MN时这个四边形为矩形，

当AC≠MN时这个四边形为等腰梯形.

矩形或等腰梯形，都是圆内接四边形，由托勒密定理得

MA·NC=MC·NA+MN·AC，

即MA2=MC2+MN·AC，

(MA+MC)(MA-MC)=MN·AC，

因此，椭圆E2的离心率

2647设R,r,p分别表示△ABC的外接圆半径、内切圆半径、半周长，求证：

(1)

(河南质量工程职业学院 李永利 467001)

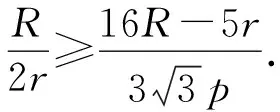
(2)

(2)式等价于

由Gerresten不等式p2≥16Rr-5r2可知，欲证上式成立，只需证明

27R2(16Rr-5r2)≥4(16Rr-5r2)2

⟺27R2≥4(16Rr-5r2)

⟺27R2-64Rr+20r2≥0

⟺(R-2r)(27R-10r)≥0.

而由Euler不等式R≥2r可知上式显然成立，故(2)式成立.

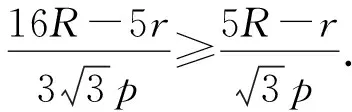
(3)

(3)式等价于

16R-5r≥3(5R-r)⟺R≥2r.

而R≥2r显然成立，故(3)式成立.

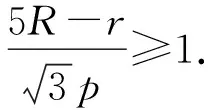
(4)

(4)式即为

由Gerresten不等式p2≤4R2+4Rr+3r2可知，欲证上式成立，只需证明

3(4R2+4Rr+3r2)≤(5R-r)2

⟺12R2+12Rr+9r2≤25R2-10Rr+r2

⟺13R2-22Rr-8r2≥0

⟺(R-2r)(13R+4r)≥0.

而由Euler不等式R≥2r可知上式显然成立，故(4)式成立.

由(2)，(3)，(4)式可得(1)式.

2648设△ABC的内切圆I与边BC，CA，AB分别切于D，E，F．记AB=c，BC=a，CA=b，若BE=CF，求证：b=c．

(湖北省公安县第一中学 杨先义 434300)

证明由内切圆的性质可知，CE=p-c，BF=p-b，其中p为半周长．由余弦定理

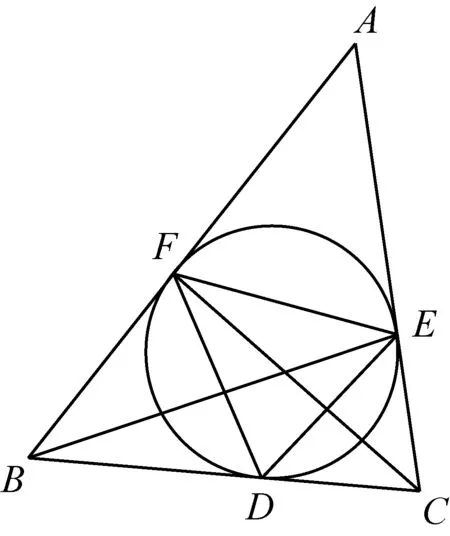
BE2=a2+(p-c)2-2a(p-c)cosC，

CF2=a2+(p-b)2-2a(p-b)cosB，

因为BE=CF，所以，

a2+(p-c)2-2a(p-c)cosC

=a2+(p-b)2-2a(p-b)cosB，

(2p-b-c)(b-c)+2a(p-b)cosB-2a(p-c)cosC=0，

整理得

2abc(b-c)+b(a-b+c)(a2-b2+c2)-c(a+b-c)(a2+b2-c2)=0，

(b-c)[2abc-b(a2-b2+c2)-c(a2+b2-c2)]+ab(a2-b2+c2)-ca(a2+b2-c2)=0，

(b-c)[2abc-b(a2-b2+c2)-c(a2+b2-c2)]+(a3b-ca3)-(ab3-c3a)+(abc2-ab2c)=0，

(b-c)[2abc-b(a2-b2+c2)-c(a2+b2-c2)]+a3(b-c)-a(b-c)(b2+bc+c2)-abc(b-c)=0，

(b-c)(a3+b3+c3-b2c-bc2-c2a-ab2-a2b-ca2)=0，

(b-c)[a2(a-b-c)+b2(b-c-a)+c2(c-a-b)]=0，

上式第二个因式显然为负，故只能有b=c．证毕．

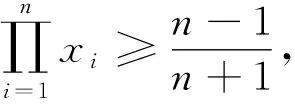
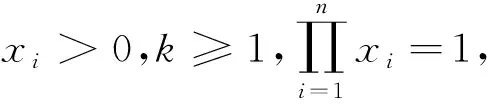
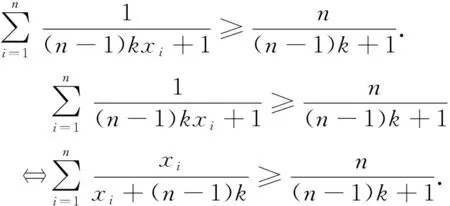
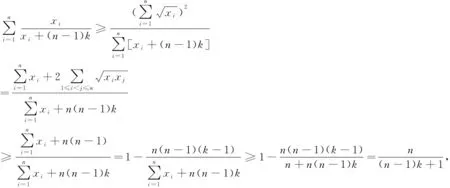
故不等式成立，当且仅当x1=x2=…=xn=1时等号成立.

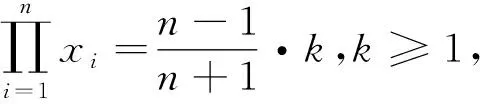
2650已知⊙O1与⊙O2相交的一个交点为A，直线BC与⊙O1、⊙O2相切于B、C,⊙O3为

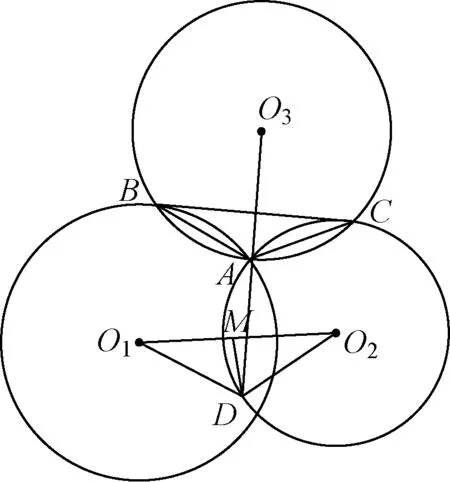
△ABC的外接圆，O3关于点A的对称点为D,点M为O1O2的中点.求证：∠O1DM=∠O2DA.

(江西省高安市石脑二中 王典辉 330818)

证明联结O1B、BO3、O3C、CO2、O1O3、O3O2、O1A、O2A.

因为O1A=O1B,O3B=O3A,

所以，O1O3是AB的中垂线，

同理可得O3O2是AC的中垂线.

延长BO1交⊙O1于N,联结NA,

因为BC切⊙O1于点B,

所以∠ANB=∠ABC,

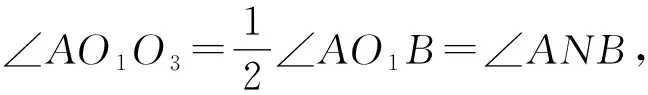
所以∠AO1O3=∠ABC.

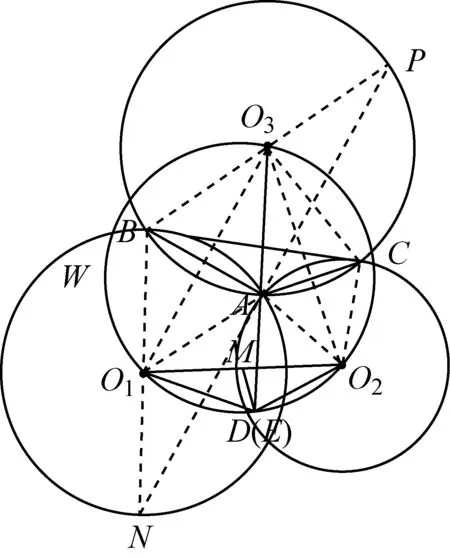
延长BO3交⊙O3于点P,联结PA,

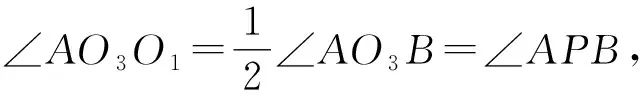
∠APB=∠ACB,

所以△O3O1A∽△CBA.

同理可证△O3O2A∽△BCA,

因此有△O3O2A∽△O1O3A.

作△O1O2O3的外接圆W,设O3A与⊙W交于另一点E,则有

∠EO1O2=∠AO3O2=∠AO1O3,

∠EO2O1=∠AO3O1=∠AO2O3,

故有△O1EO2∽△O1AO3∽△O3AO2,

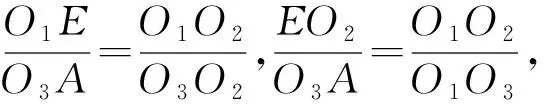
因此有

O1O2·O3A=O1E·O3O2,

O1O2·O3A=EO2·O1O3,

①

所以O1E·O3O2=EO2·O1O3.

因此四边形O1O3O2E为调和四边形,

在⊙W的内接四边形O1O3O2E中,由托勒密定理有

O1O3·EO2+O3O2·O1E=O3E·O1O2，

O1O3·EO2+O3O2·O1E

=(O3A+AE)·O1O2，

2O1O3·EO2=O3A·O1O2+AE·O1O2，

2O1O2·O3A=O3A·O1O2+AE·O1O2，

O3A=AE.

因为O3A=AD,所以点E与点D重合.

在⊙W的内接四边形O1O3O2D中,根据托勒密定理,有

O1O3·DO2+O3O2·O1D

=O3D·O1O2.

因为点M为O1O2的中点,

所以O1O2=2MO2.

把此式代入上式,得

2MO2·O3D

=O1O3·DO2+O3O2·O1D,

MO2·O3D

=O1O3·DO2;

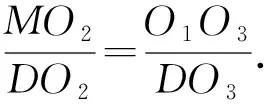
因为∠O1O3D=∠MO2D,

所以△O1O3D∽△MO2D,

即有∠O1DO3=∠MDO2,

故∠O1DM=∠O2DA.

2022年3月号问题

(来稿请注明出处——编者)

2651在△ABC中，三内角A、B、C所对的三边长分别为a、b、c，面积为Δ，求证：

(浙江省开化县第二中学 曹嘉兴 324300)

2652如图，在四边形ABCD中，E，F分别是AC，BC的中点，求证：AF⊥DE，AC⊥DF，AB⊥AD知二推一.

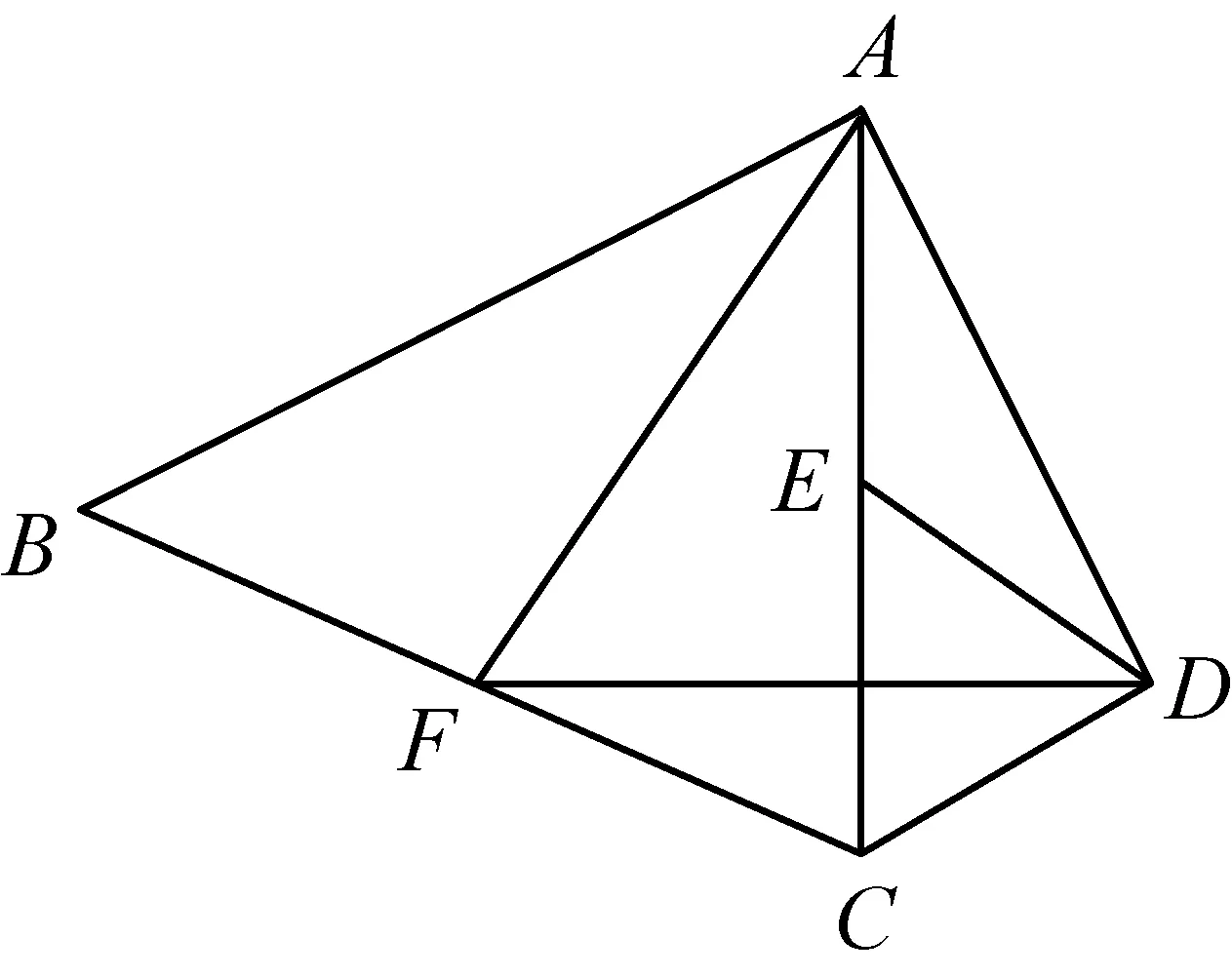
(山西省临县一中 李有贵 033200)

2653设a,b,c,d>0,且a+b+c+d≤4,求证：(abcd)3(a3+b3+c3+d3)≤4.

(浙江省杭州二中未来科技城学校 李盛 311121)

(山东省泰安市宁阳第一中学 刘才华 271400)

2655已知m=(sinx,cosx)，n=(cosx,-cosx)，设f(x)=m·n，若锐角△ABC满足f(C)=0，且不等式tan2A+tan2B+ptanAtanB+1≥0恒成立，求p的取值范围.

(江苏省启东市汇龙中学 倪红林 226200)