三维微分系统的极限环与等时中心

黄文韬， 古结平， 王勤龙

(1.广西师范大学 数学与统计学院， 广西 桂林 541006； 2.广西职业师范学院 教育学院， 广西 南宁 530007；3.桂林电子科技大学 数学与计算科学学院， 广西 桂林 541004)

近百年来，常微分方程定性理论得到迅速发展, 已在无线电技术、天体力学、航空工程、自动控制、生物学和经济学等众多领域中得到广泛应用，同时应用技术的发展也反过来促进微分方程定性理论的发展。微分动力系统的极限环分支和等时中心问题是微分方程定性理论中相互关联的经典问题，其研究具有重要的理论意义和应用价值。

微分系统的极限环研究来自实践，许多应用学科如物理学、力学、生物学、经济学、生态学、电子学和金融学等领域都可能出现极限环现象，极限环在非线性系统动力学研究中扮演着非常重要的角色。极限环是世界著名数学家庞加莱(Poincaré)[1]19世纪后期最先发现，随后的进一步发展受著名的Hilbert 23个数学问题中的第16问题[2]所推动，成为微分方程定性理论研究的主要问题之一。然而，Hilbert第16问题自1900年第二届国际数学大会提出后，至今仍未解决，对于简单的平面二次系统的极限环最大个数及其位置分布问题仍是开放问题。关于平面微分系统的极限环分支研究，国内外已产生丰富的研究成果，可参看综述文献[3-4]。

中心-焦点问题(Poincaré中心问题)与极限环分支研究紧密相连，解决以上2个问题都涉及焦点量或Lyapunov常数的计算。对经典中心问题，很多工作已经完成，见文献[5-7]及其中的参考文献。如果一个系统的奇点是中心(奇点附近的所有解都是周期性的)，那么自然产生的问题是中心点附近的所有解是否具有相同的周期，这就是等时中心问题，其研究不仅是微分方程定性理论中的一个重要领域，而且在实际中也有应用[8]。等时中心问题的第一个非线性例子，最早可追溯到1673年荷兰数学家、物理学家惠更斯(Huygens)所设计的旋轮摆钟[9]。然而等时中心问题的研究直到20世纪下半叶才开始引起重视，并出现大量研究成果，例如文献[10-13]及文中的参考文献。

在实际中，微分方程所描述的数学模型的维数往往会大于2[14]，因此，对三维甚至更高维系统的极限环分支和等时中心问题的研究也很重要。当极限环分支和等时中心研究从平面微分系统扩展到n维系统(n≥3)，系统复杂性和定性分析难度相较于二维系统都有很大提升，奇点邻域内所具有的极限环最大个数与中心等时性问题将会变得更具有挑战性，这是因为高维向量场中不仅可能存在极限环分支行为，而且可能有更加复杂的动力学行为，例如混沌[15]。

近几十年来，计算机科学技术的迅速发展给微分方程定性理论研究带来十分便捷的工具，特别是符号计算系统的出现与推广极大促进了极限环分支和等时中心的研究，一些三维系统甚至高维系统在不变曲面上的极限环分支与等时中心问题开始得到探索。本文将针对三维光滑系统，如Lotka-Volterra系统，Lorenz、Chen和Lü系统以及三维分片光滑系统，介绍其极限环分支与等时中心的一些研究进展。

1 不变曲面上具有Hopf分支的三维多项式系统

对于三维多项式实系统

(1)

式中Pn(x,y,z)、Qn(x,y,z)和Rn(x,y,z)是n次多项式函数。若系统(1)在原点(0,0,0)有1个孤立的Hopf奇点，即系统(1)在奇点(0,0,0)的线性化矩阵有一对纯虚特征值和一个实特征值，则系统(1)可以通过一个坐标变换与时间尺度变换转化为如下形式的三维多项式系统

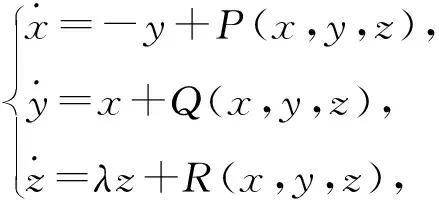
(2)

式中x、y、z、λ∈R,P(x,y,z)、Q(x,y,z)和R(x,y,z)是次数至少为2的多项式函数，且P(0,0,0)=Q(0,0,0)=R(0,0,0)=0。通常极限环定义在二维平面上，而对三维或更高维系统的Hopf分支(当系统参数发生微小变化时在奇点附近产生极限环的现象)问题，往往需要限制在一个二维不变流形上讨论，如此便可将平面极限环的定义和Poincaré-Bendixson定理等推广到三维或更高维系统。

目前，对于一般三维多项式光滑系统的极限环和等时中心研究主要集中于二次系统，而且关于极限环的大部分结果属于扰动细焦点情形，有少量结果是扰动中心情形，下面介绍相关成果。

2010年，Wang等[16]研究如下形式的三维非线性动力系统在中心流形上的Hopf分支问题

(3)

式中x、y、u、d、Akjl、Bkjl、dkjl∈R(k、j、l∈N)。给出一种与逐项待定中心流形过程同步计算系统(3)在中心流形上分支点的奇点量递推算法，证明奇点量和对应焦点量之间的代数等价关系。作为方法的应用，该文同时考虑如下三维三次多项式系统的例子

(4)

式中δ、d>0、Akjl、Bkjl、Dkjl∈R。利用奇点量递推算法计算得到系统(4)的前5阶奇点量，获得5个小振幅极限环围绕单一奇点的结果。该算法省掉了传统方法中需要降维和计算中心流形的过程，并且是递推的，避免复杂积分运算和解方程，便于在计算机代数软件上编程实现。这种不需计算中心流形而直接得到高维系统焦点量的方法还有Tian等[17]和Romanovskic等[18]给出的方法。文献[17]的方法还可以求三维以上系统的焦点量与周期常数，但出现多层求和运算，计算较复杂。

2014年，Tian等[19]考虑如下三维二次系统在中心流形上的多重Hopf分支问题

(5)

式中α、β>0且aij、bij、cij(i,j=1,2,3)为参数。系统(5)的前2个方程采用Bautin方程形式(任何具有围绕奇点的周期轨道的二次系统都可通过适当的旋转变换得到这一形式)。显然，对任意参数值，原点都是系统(5)的平衡点，且当α=0时，原点为Hopf临界点。考虑a13=a23=a33=b13=b23=b12=c11=c22=c23=0,β=b11=c12=1情形，得到如下最简三维二次系统

(6)

通过系统(6)焦点量的计算，证明了以下极限环分支结果(定理1)。

定理 1[19]系统(5)的参数a11、a12、a22、b33、c33、c13为任意非零常数，则至少有7个小振幅极限环围绕系统(5)的原点。

对比Bautin[20]1952年获得平面二次向量场从单个初等焦点或初等中心可分支出3个小振幅极限环的结果，定理1证明了三维二次向量场从单个平衡点可分支出比3个更多的极限环，获得二次向量场极限环个数的一个新下界。

上述系统(4)、(5)考虑从单一细焦点分支出极限环的情形。对中心的情形，2015年，Yu等[21]也研究系统(5)的极限环个数，不同的是，取系统(5)的系数为α=a33=a13=a23=b33=b13=b23=c11=c22=c13=c23=0,β=b11=c12=c33=1,a22=-a11，得到一个具有中心类型奇点的三维二次系统，添加二次扰动项，获得如下扰动系统

(7)

式中0<ε≪1是扰动参数。当ε=0时，根据Bautin[20]的结论，系统(7)限制在中心流形上的原点是一个中心。当ε≠0时，通过对系统(7)的参数进行微扰，得到定理2。

定理 2[21]通过适当选择扰动参数aij0、bij0、cij0以及系统系数a11、a12, 系统(7)至少有10个小振幅极限环从原点分支出来。

相比前面通过扰动三维二次系统(5)的细焦点而得到的7个小振幅极限环的结果，定理2获得的10个极限环从数目上更进一步。

最近，Sánchez等[22]考虑二次、三次、四次和五次系统(2)|λ=1限制在中心流形上的中心环性数问题，得到定理3～6。

定理 3[22]二次系统

在原点处有一个中心，在完全二次扰动下，该系统存在11个极限环。

定理 4[22]三次系统

在原点处有一个中心，在完全三次扰动下，系统存在31个小振幅极限环。

定理 5[22]四次系统

在原点处有一个中心，在完全四次扰动下，系统存在54个小振幅极限环。

定理 6[22]五次系统

在原点处有一个中心，其中f(x,y)=(1-x-y)(1+2x-y)，且在完全五次扰动下，该系统存在92个极限环。

文献[22]获得的极限环结果采用并行运算方法来计算Lyapunov常数。另外，定理3得到的11个极限环结果是目前关于三维二次系统从单一奇点分支出极限环个数的最好结果。除了扰动系统单一奇点产生极限环的结果，还有学者研究系统对称奇点产生极限环的问题。2014年，Du等[23]利用文献[16]所给奇点量方法,研究如下三维二次系统的极限环问题

(8)

式中A、B、C为实参数。系统(8)中将变量x变为-x是不变的，因此位于一个对称向量场上，称为“YOU”对称(系统关于“y-o-u”平面对称)。显然，系统(8)有2个对称奇点(1,1,1)和(-1,1,1)。这2个奇点在三维向量场中具有相同拓扑结构，因此只需研究其中一个奇点的Hopf分支。运用文献[16]提出的奇点量方法，利用计算机代数系统计算，得到奇点(1,1,1)的前4阶奇点量，给出定理7。

定理 7[23]系统(8)的奇点(1,1,1)成为一个4阶细焦点当且仅当下列条件之一成立

基于定理7中细焦点阶数条件，得到定理8。

定理 8[23]假设系统(8)的奇点(1,1,1)是一个4阶细焦点，则在一定参数扰动条件下，系统(8)的奇点(1,1,1)能分支出4个极限环，其中2个极限环是稳定的。相应地，系统(8)一共能分支出8个极限环，其中4个极限环是稳定的。

2016年，Du等[24]研究如下三维二次对称系统的Hopf分支问题

(9)

式中：B1、B2、C1、C2是实参数，δ是充分小的实参数，且系统(9)|δ=0“YOU”对称。当δ=0时，点(1,0,1)和(-1,0,1)是系统的2个对称奇点。运用文献[16]方法计算系统(9)|δ=0奇点(1,0,1)的前5阶Lyapunov常数，得到定理9～10。

定理 9[24]系统(9)|δ=0的奇点(1,0,1)成为一个5阶细焦点当且仅当下列条件成立

式中m3、m4是关于C1、C2的表达式。

定理 10[24]在一定参数扰动条件下，系统(9)的奇点(1,0,1)能分支出5个极限环，其中3个是稳定环，而且系统(9)一共能分支出10个极限环，其中6个是稳定环。

Guo等[25]2018年考虑如下系统

(10)

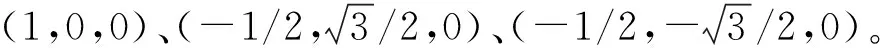
(11)

式中系数Aij、Bij、Cij是实参数, 系统(10)的奇点(1,0,0)对应于系统(11)的原点。运用规范形方法计算得到系统原点的前4阶焦点量表达式。进一步，运用结式与行列式方法证明以下定理11，获得三维二次系统极限环个数的一个新下界。

众所周知，运用计算机软件模拟3个以上极限环很困难。模拟m(m≥3)个极限环的难点主要在于如何适当地从临界点选择参数扰动，使截断的规范形具有m个正实根。若扰动可以逐步进行，并且每一步扰动一个参数，那么这个过程仍然很简单。然而，如果规范形的多项式方程是耦合的，那么要找到合适的扰动非常具有挑战性。文献[25]给出一种模拟4个极限环的方法，模拟结果与定理11的结论一致。

2019年，Guo等[26]受文献[24]启发，考虑如下三维二次系统在中心流形上的极限环问题

(12)

式中a1、b1、b2、b3、c1、c2、c3是实参数，满足a1>0,b3>0,c3>0,|δ|≪1。显然系统(12)也是“YOU”对称的，具有2个对称奇点(1,0,1)和(-1,0,1)。为减少系统(12)参数，引入如下尺度变换

系统(12)变为如下系统

(13)

系统(13)相比系统(12)减少2个参数，简化了系统的定性分析难度。对系统(13)再引入变换

x=y1+1,y=x1,u=u1+1,

则转换为如下系统

(14)

利用规范形理论，文献[26]证明定理12，是目前关于三维二次对称系统极限环个数的最好结果。

定理 12[26]系统(12)有12个呈6-6分布的极限环围绕2个对称奇点(1,0,1)和(-1,0,1)。

在此基础上，Guo等[26]找到系统(14)的一个全局中心流形，解决了系统(12)的中心问题。

定理 13[26]对系统(14)|δ=0，当C2=0时，Γ∶u1=0是系统的一个不变代数曲面(定义了全局中心流形)，且原点是限制于该中心流形上的中心(即当C2=0时，系统(12)|δ=0的临界点(1,0,1)和(-1,0,1)是中心)。

如果一个系统的奇点是中心(奇点附近的所有解都是周期性的)，那么自然产生的问题是中心点附近的所有解是否具有相同的周期，这就是等时中心问题。Guo等[26]在求得系统(14)的一个中心流形,得到系统的中心条件后，继续考虑等时中心问题。通过将中心流形代入三维系统降为平面系统，再利用平面系统周期常数的计算方法以及寻找线性化变换，文献[26]证明系统(14)的以下2组等时中心条件。

定理 14[26]对系统(14)，假设δ=0且C2=0，则：

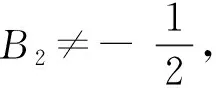
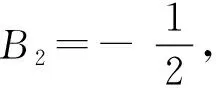
值得一提的是，Guo等还给出中心与极限环的数值模拟结果，进一步说明前面得到结果的正确性。在模拟三维微分系统的中心和极限环方面，由于技术上的困难，目前相关结果很少。

2021年，Li等[27]研究如下对称三维二次系统的极限环和可积性问题

(15)

式中b6、b7、b8、c2、c4、c6、c8是实参数；(0,0,0)和(-2,0,0)是系统(15)的2个对称奇点。系统(15)的可积性条件在定理15中给出。

定理 15[27]系统(15)在原点邻域有一个解析的局部首次积分当且仅当下列条件之一成立

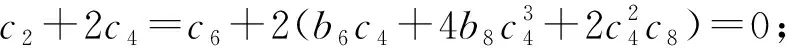
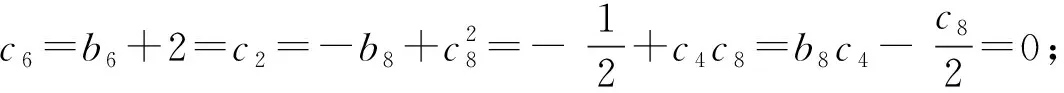
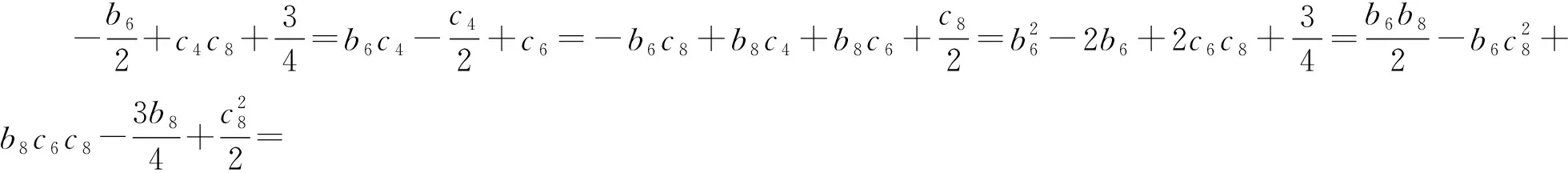
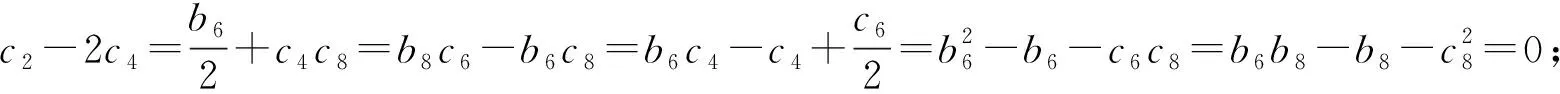
⑤b8=0。

在定理15可积性条件基础上，作者研究了系统(15)中心的环性数问题，得到定理16。

定理 16[27]对于定理15中给定的条件①、②、③、④、⑤，系统(15)原点的环性数分别为2、5、4、4、1。

由于系统(15)的对称性，对系统的奇点(-2,0,0)也有相同的可积性与极限环结论。

关于三维光滑多项式微分系统在中心流形上的等时中心问题(可线性化问题)，Edneral等[28]2012年考虑如下三维微分系统

(16)

在中心流形上的动力学性质，利用形式级数法解决了系统(16)在中心流形上的中心-焦点判定问题，找到了中心流形上的如下5组中心条件：

①S=0;

②a=b=c+f=8c+T2-U2=4(e-d)-T2U2=2(e+d)+TU=0,S=1;

③a=b=c=f=d+e=0,S=1;

④d+e=c=f=T-2a=U-2b=0,S=1;

⑤c=d=e=f=0,S=1。

(17)

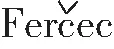
(18)

的等时中心问题。他们首先求出系统的一个中心流形u2+v2-w=0，把三维系统(18)降维到平面系统，再用平面动力系统的方法研究三维系统在中心流形上的等时中心问题，证明得到系统(18)原点在中心流形上成为等时中心的2组充分必要条件，即定理17。

定理 17[29]系统(18)是可线性化的当且仅当下列条件之一成立

①a01b10+b11=b10=a11-b11=0;

②a01b10+b11=a01=a11-b11=0。

式中：a11=d；a01=-b+ia；b11=d；b10=-b-ia。

2013年，Romanovski等[30]继续研究系统(16)在其余4个中心条件下的中心等时性问题，给出以下等时中心和临界周期分支结果(定理18～21)。

定理 18[30]当中心条件(17)中的①满足时，系统(16)有1个等时中心当且仅当a=b=0，且系统(16)的中心没有临界周期分支。

定理 19[30]当中心条件(17)中的②满足时，系统(16)有1个等时中心当且仅当α=β=0，且系统(16)的中心没有临界周期分支。

定理 20[30]当中心条件(17)中的③满足时，系统(16)有1个等时中心当且仅当d=0，且系统(16)的中心没有临界周期分支。

定理 21[30]当中心条件(17)中的④满足时，在微小扰动下，从系统(16)在中心流形上的中心至多能分支出一个临界周期，且能扰动出1个临界周期。

2013年，Hu等[31]考虑如下具有3个不变平面的三维多项式系统的可积性与可线性化问题

(19)

借助计算机代数系统的符号计算，找到系统(19)的12组可积性条件和12组可线性化条件，通过构造系统(19)的达布(Darboux)积分因子和雅可比(Jacobi)积分因子，证明可积性条件的充分性，利用达布可线性化理论证明系统(19)的12组可线性化条件。

2019年，Wang等[32]给出一种不需要计算三维系统的中心流形，直接找出等时中心条件的方法。他们定义了三维多项式系统(3)的等时常数并给出递推算法，同时考虑如下Moon-Rand系统

(20)

和一类复三维二次系统

(21)

在中心流形上的等时中心问题作为方法的应用。利用三维系统等时常数递推算法找出系统(20)、(21)的等时中心条件，运用待定Darboux不变曲线或曲面方法，找到线性化变换，证明条件的充分性。

定理 22[32]系统(20)的原点是一个等时中心当且仅当c1=c2=c3=0。

定理 23[32]系统(21)的原点是一个等时中心当且仅当以下条件之一成立

①b1=b2=0; ②a1=a2=0; ③b1=a2=0; ④a2=-a1,b1=-b2。

在三维光滑对称系统的等时中心研究方面， Li等[33]研究如下三维对称二次系统在中心流形上的等时中心问题

(22)

式中b6、b8、c2、c4、c6、c7、c8是实参数。显然系统(22)的2个奇点A(-2,0,0)和B(0,0,0)关于平面x=-1对称，属于“YOU”对称型。按c7=0和c7=1两种情形研究系统(22)在中心流形上的可线性化问题，定理24、25。

定理 24[33]具有c7=0的系统(22)在中心流形上是可线性化的当且仅当下列条件之一成立

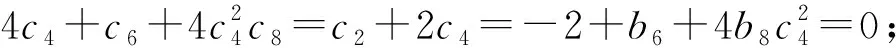
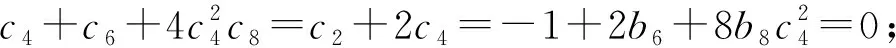
③b8=b6-2=0;

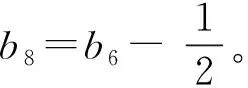
此外，在每一种情况下，系统(22)在中心流形上都是可线性化的。

定理 25[33]具有c7=1的系统(22)在中心流形上是可线性化的当且仅当下列条件之一成立

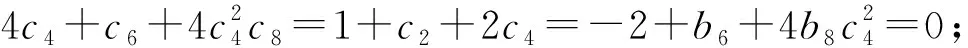
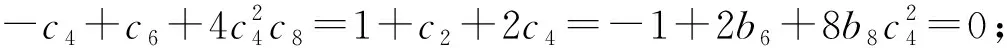
③b8=b6-2=0;

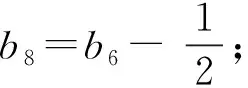
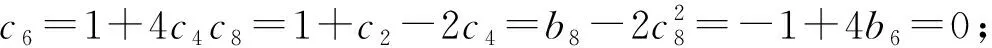
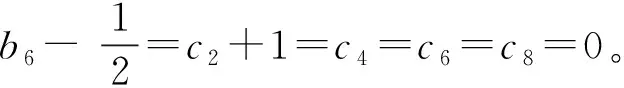
2 三维Lotka-Volterra系统

近几十年来，在许多生物系统中已经研究了极限环问题[34-35]，比较著名的例子就是三维Lotka-Volterra (LV)系统。本章将介绍三维LV系统在中心流形上的极限环分支和等时中心研究成果。考虑如下形式的三维LV系统

(23)

这是三维二次系统的特殊情形，该系统的动力学性质具有重要的生物学意义[34]。当ri>0,aij>0(i,j=1,2,3)时，系统(23)称为三维LV竞争系统，描述的是3个物种之间共享和争夺同一资源、栖息地或领土的关系。一般来说，系统(23)共有8个平衡点，包括原点、1个正平衡点、3个轴向平衡点和3个平面平衡点。考虑到其生物学意义，一般研究正平衡点的动力学性质。不失一般性，假设系统(23)的正平衡点为(1,1,1)。

众所周知，二维LV系统不会出现极限环分支现象[36]，而对于一般三维LV系统，已经发现其存在复杂的动力学行为，例如倍周期混沌路径[37]。1979年，Coste等[38]首次证明三维LV竞争系统极限环的存在性。之后，在Hirsch定理[39]的基础上，Zeeman[40]1993年给出三维LV竞争系统的33种稳定等价类，并证明只有其中6类(第26～31类)能够产生极限环，且仅第27类可能有异宿环。剩余27类系统的紧极限集都是不动点，因此，这些类下的系统动力学行为已得到充分描述。第26～31类LV系统能有多少个极限环的问题，吸引了众多学者的研究兴趣，目前已取得一些成果，主要集中于三维LV竞争系统，有少部分结果是关于三维LV非竞争系统的极限环研究。

作变换ui=xi-1,i=1,2,3，系统(23)可转化为

(24)

记系统(24)在原点(0,0,0)的Jacobian矩阵为 -A，称A为相互作用矩阵。1994年，Hofbauer等[41]给出1个第27类的三维LV竞争系统例子，该系统的相互作用矩阵为

其中μ=71/48=1.479 666…。该系统存在1个亚临界的Hopf分支：第1个焦点量是正的。作者证明了这类系统至少存在2个极限环，其中一个是通过Hopf分支产生的小振幅极限环，另一个是由于异宿环的存在，运用Poincaré-Bendixson定理证明得到的大环。同时他们还提出猜想1。

猜想 1[41]对于三维LV竞争系统(23)，在单形(carrying simplex)边界上的异宿环情形下，下列条件等价于系统有一个中心：

① 在正平衡点有一对纯虚特征值；

② 第1个焦点量为零；

③ 异宿环是中性稳定的，此外，条件③可以被条件④取代；

④ 第2个焦点量为零。

注Carrying simplex是系统(23)的一个不变流形，即它与二维单形同胚，且吸引除原点之外的所有轨道。

2000年，Xiao等[42]证明对于没有任何异宿环的三维LV竞争系统，其所分支出的极限环个数有限，即定理26。

定理 26[42]存在平衡点E(1,1,1)的一个小邻域，使得在这个邻域内方程(23)的极限环个数是有限的，即方程(23)在E(1,1,1)周围不可能存在无穷多个极限环。

此外，文献[42]还讨论如下1个属于第27类的三维LV竞争系统

(25)

式中ε1和ε2是小参数。类似文献[41]中例子，系统(25)至少存在2个极限环，其中一个是由Hopf分支产生的小振幅极限环，另一个是由于系统存在一个异宿环，运用Poincaré-Bendixson定理证明得到的大环。

2002年，Lu等[43]考虑如下三维LV竞争系统

(26)

式中aij<0且1=(1,1,1)是系统(26)唯一的正平衡点。这个系统可写成向量形式

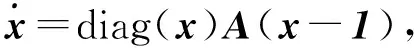
(27)

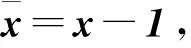
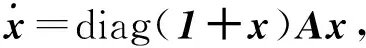
(28)

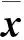
det(A)=(A11+A22+A33)tr(A)<0,

(29)

式中A11=a22a33-a23a32,A22=a11a33-a13a31,A33=a11a22-a12a21。他们分别给出了第26～29类的三维LV竞争系统例子，即在系统(28)中分别取

式中参数μ分别取

使得矩阵A满足式(29)。文献[43]证明这些系统都至少存在2个极限环，其中第27类系统有一个异宿环。紧接着，Lu等[44]考虑1个具有如下相互作用矩阵A的第27类系统

其中μ=-117/8-(633/640)λ，证明这个系统存在3个极限环，其中2个是通过Hopf分支产生的小振幅极限环，第3个大极限环是由于异宿环的存在性，运用Poincaré-Bendixson定理证明得到。

2006年，Gyllenberg等[45]考虑如下1个第29类三维LV竞争系统

(30)

式中

这里μ和λ是正参数，且μ=148 137 475/100 576 964-(11 422 593/100 576 964)λ，证明三维LV竞争系统(30)存在3个小振幅极限环。2009年，Gyllenberg等[46]构造了1个第27类三维LV竞争系统

(31)

其中

这里μ、λ和n是负参数，且μ=-3(-312+11λn)/(50n)。文献[46]证明了三维LV竞争系统(31)存在4个极限环，其中1个是由于系统存在一个异宿环，运用Poincaré-Bendixson定理证明得到的大环，剩余3个是通过Hopf分支产生的小振幅极限环。

前面已提到的第27类三维LV竞争系统的极限环成果中，Lu等[44]和Gyllenberg等[46]通过构造第27类三维LV竞争系统，分别证明3个和4个极限环的存在性，这些结果反驳了Hofbauer和So在1994年提出的猜想1，同时Gyllenberg等还在文献[46]中提出一个新猜想。

猜想 2[46]

(ⅰ)三维LV竞争系统(31)至少有5个极限环。

(ⅱ)对系统(31)，在carrying simplex边界上存在异宿环的情形下，猜想1条件①、②、④和

⑤ 第3个焦点量为零，

不能推导出条件③。特别地，条件①、②、④和⑤不会意味着正平衡点是一个中心。

(ⅲ)对系统(31)，在carrying simplex边界上存在异宿环的情形下，条件①、②、③和④不能推出条件⑤。特别的，条件①、②、③和④不会意味着正平衡点是一个中心。

在第30、31类三维LV竞争系统的极限环个数问题研究方面，相关研究成果很少。直到2009年，Gyllenberg等[47]给出2个属于第30、31类三维LV竞争系统的例子，即在系统(31)中分别取相互作用矩阵为

这里μ和λ是负参数，且

文献[47]证明这2个系统都至少存在2个极限环，其中一个极限环是通过Hopf分支产生的小振幅极限环，另一个极限环是由异宿环的存在性，以及运用Poincaré-Bendixson定理证明得到的大环。

2011年， Wang等[48]考虑具有如下相互作用矩阵A的三维LV竞争系统

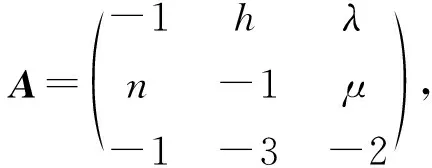
式中λ、μ、h、n是负参数，且

利用奇点量方法和Poincaré-Bendixson定理研究第26～31类三维LV竞争系统的极限环分支问题，证明第26～31类三维LV竞争系统至少存在3个小振幅极限环。特别地，第27～29类三维LV竞争系统有4个极限环，其中第29类三维LV竞争系统的极限环个数，目前仍是最好结果。

2016年，Yu等[49]对第26、27类三维LV竞争系统的极限环问题进行探索，构造2个具有如下相互作用矩阵A的第27类三维LV竞争系统

式中pi>0，i=1,2,3,4。通过计算系统正平衡点的焦点量，证明这2个系统经过Hopf分支至少可产生4个小振幅极限环，此外还证明了Gyllenberg等[46]所提出猜想2中的(ii)和(iii)。另外，还构造了2个具有如下相互作用矩阵A的第26类三维LV竞争系统

其中pi>0,i=1,2,3,4。同样通过计算系统正平衡点的焦点量，证明这2个系统经过Hopf分支至少可产生4个小振幅极限环，这是目前第26、27类三维LV竞争系统从单一奇点分支出极限环个数的最好结果。

到目前为止，已发现第26～31类三维LV竞争系统的极限环最大个数是4。然而，第26～31类三维LV竞争系统最多有几个极限环仍然是一个开放问题。

非竞争性的三维LV系统的极限环研究比较少，Wang等[50]2011年构造1个具有如下相互作用矩阵A的三维LV非竞争系统

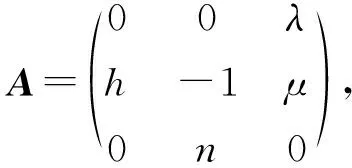
(32)

其中μ=hλ。利用奇点量方法，得到定理27、28。

定理 27[50]系统(32)的平衡点E(1,1,1)是一个4阶细焦点当且仅当n=(h+2ω2)/h，h=2ω2(1-6ω2)/(ω2-1)，且ω=ω0≈0.321 8。

定理 28[50]若定理27的条件成立，则从系统(32)的平衡点E(1,1,1)能分支出4个极限环。

最近，Wang等[51]考虑1个具有如下相互作用矩阵A的三维LV非竞争系统

(33)

式中：n、h、s、v、λ是实数；v=-ω2-hn；λ=s/h,hs<0。文献[50]证明该系统的平衡点E(1,1,1)最多能分支出5个极限环，这是目前关于三维LV系统从单一奇点分支出极限环个数的最好结果。

在三维LV系统的等时中心或可线性化问题研究方面，近几年有一些成果。2012年，Aziz等[52]分别考虑原点是(1∶-1∶1)、(2∶-1∶1)和(1∶-2∶1)共振临界点的三维LV系统

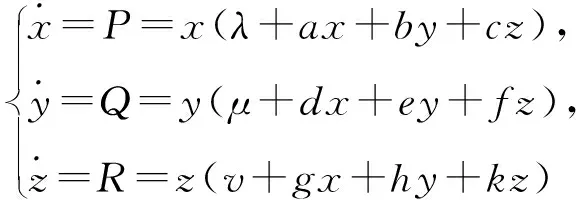
(34)

的可积性和可线性化问题。通过逐一分析这3种共振情形，分别得到系统(34)的7组、11组和25组可积性条件。在此基础上，分别证明系统(34)存在10组、13组和23组可线性化条件。

2019年，Aziz[53]研究如下三维LV系统在原点的局部可积性和可线性化问题

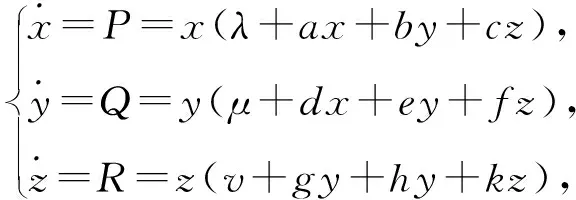
(35)

式中(λ∶μ∶v)=(1∶3∶-1)。首先给出系统(35)在原点处可积的15组条件，在此基础上，得到系统(35)的16组可线性化条件。

最近，Aziz等[54]研究三维LV系统

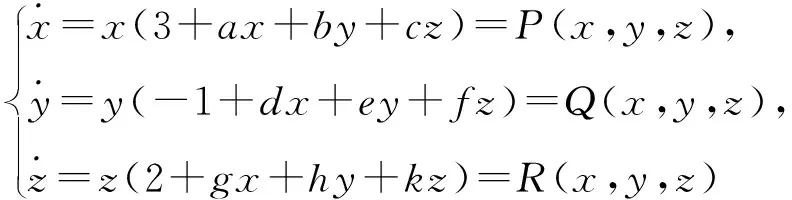
(36)

在原点的局部可积性和可线性化问题。利用Darboux方法证明系统(36)在原点处可积，并给出20组可积性条件，在此基础上得到系统(36)的20组可线性化条件。

3 Lorenz、Chen和Lü系统

1963年，荷兰气象学家洛伦兹(Lorenz)[55]在研究大气中热流体对流时引入如下著名的Lorenz系统

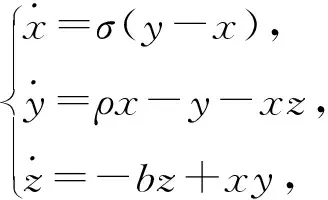
(37)

式中σ和ρ分别是Prandtl数和Rayleigh数，b是对流圆柱体的纵横比。Lorenz系统形式简洁，但蕴含丰富的动力学行为，由于涉及长期天气预报问题，吸引了众多学者的关注。Lorenz系统在变换(x,y,z)→(-x,-y,z)下不变，对所有参数(ρ,σ,b)，原点是系统的孤立奇点。此外，当b(ρ-1)>0时，系统还存在一对非平凡的孤立对称奇点

众所周知，如果Lorenz系统的3个参数ρ、σ、b都为正数，那么原点处不会出现Hopf分支，但非平凡平衡点E±会出现亚临界Hopf分支。

如下Chen系统[56]

(38)

和Lü系统[57]

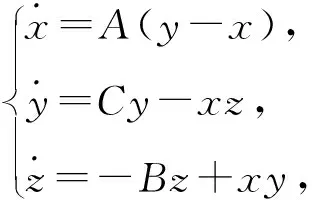
(39)

式中参数(A,B,C)∈R3。经过时间变量和状态变量的线性缩放后，Chen系统和Lü系统一般可简化为Lorenz系统的特例。下面介绍Lorenz、Chen和Lü系统的一些可积性与极限环研究进展。

近几十年来，多位学者从可积性角度，利用不同可积性理论对Lorenz系统(37)进行深入研究，例如文献[58-62]。2002年，Llibre等[63]对Lorenz系统(37)的达布不变量、不可约达布多项式、有理首次积分和代数可积性进行完整分类。在此基础上，Zhang[64]2002年运用权值齐次多项式和达布可积性理论，描述系统(37)的所有指数因子和达布首次积分。2005年，Llibre等[65]考虑系统(37)的形式可积性和解析可积性，给出定理29、30。

定理 29[65]若σ=0，则Lorenz系统(37)可积，具有2个首次积分

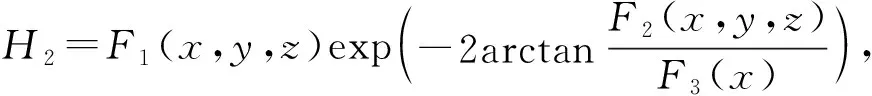
式中：

F1=x(ρ2x3-(1+b)ρx2y+bxy2+x3y2+b(b-1)ρxz-2ρx3z-b(b-1)yz+(1-b)x2yz+bxz2+x3z)；

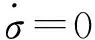
基于定理30，可以得到如下Lorenz系统可积性结论(定理31、32)。

定理 31[65]假设σ≠0且b不是负有理数，那么Lorenz系统(37)没有形式幂级数首次积分。特别地，系统(37)在原点邻域没有解析首次积分。

定理 32[65]假设σ≠0且b满足非共振条件k1b+k2(1+σ)≠0(∀k1,k2∈Z+,k1+k2>0),那么Lorenz系统(37)在原点邻域没有任何解析首次积分。

2003年，Li等[66]首次研究Chen系统(38)的Hopf分支，运用分析方法和分岔图辅助分析，得到极限环分支结论：当C>0时，有l1(0)<0，所以Hopf分支是非退化和超临界的，即对参数A0，所以Hopf分支是非退化和亚临界的，即对参数A>A0(C)=3C/4，经Hopf分支可从系统(38)的平衡点分支出唯一且不稳定的极限环。

2009年，Mello等[67]研究Lü系统(39)的余维1、2和3 Hopf分支，证明参数空间中存在一条直线C1={(A,B,C)∈R3∶A≠0,B=A/5,C=Cc}，其中非平凡平衡点Q±是余维2的Hopf点，从系统(39)的平衡点Q±能分支出2个极限环。另外，文献[67]还有以下猜想：对于直线C2={(A,B,C)∈R3∶A≠0,B=2A,C=Cc}上的参数值，系统(39)在中心流形上的非平凡平衡点Q±是非线性中心。Mahdi等[68]2011年证明了这个猜想，得到了该系统的局部中心流形是代数规则曲面，并且该曲面是唯一的结论。

2012年，Llibre等[69]利用权值齐次多项式和求解偏微分方程的特征方法，描述了Chen系统(38)和Lü系统(39)具有多项式首次积分的所有参数值。

定理 33[69]对于A≠0，Chen系统(38)有1个多项式首次积分当且仅当B=C=0。在此情况下，任何多项式首次积分都是变量y2+z2+2az的一个多项式。

定理 34[69]对于A≠0，Lü系统(39)有1个多项式首次积分当且仅当B=C=0。在此情况下，任何多项式首次积分都是变量y2+z2的一个多项式。

2012年，Wang等[70]考虑Chen系统(38)在中心流形上多重极限环的存在性问题，给出定理35～37。

定理 35[70]Chen系统(38)的平衡点Ei(i=1,2)是2阶细焦点当且仅当

2A3-2A2C-2AC2-C3=0,即A=κ0C,

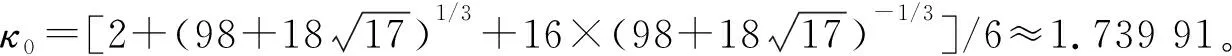
定理 36[70]存在Chen系统(38)的某些扰动系数，使得在原点的足够小邻域内有2个极限环。

定理 37[70]在定理36条件下，Chen系统(38)经Hopf分支存在4个小振幅极限环。

Wang等[71]还研究了Lü系统(39)的多重Hopf分支，证明Lü系统(39)经Hopf分支也同样有4个小振幅极限环围绕2个非平凡对称奇点。

2014年，Algaba等[72]研究Lorenz、 Chen和Lü系统在中心流形上的Hopf分支问题，给出定理38～40。

定理 38[72]Lorenz系统(37)的原点发生Hopf分支的条件由下式给出

σ=-1,ρ>1,b≠0。

当b>-2时，产生超临界分支；当b<-2时，呈现亚临界分支；当b=-2时，出现无穷余维的退化Hopf分支。

定理 39[72]Lorenz系统(37)的非平凡平衡点在半直线上(在中心流形上的中心)发生余维无穷的Hopf分支的条件为σ=-1,b=-2,ρ>1。

定理 40[72]Lorenz系统(37)的非平凡平衡点在以下2个点(σ,ρ,b)∈Shnt发生余维3的Hopf分支

P1≈(-0.646 547,-6.605 871,-1.709 567),

P2≈(-0.010 001 2,-0.039 696 5,-1.408 456)。

此外，这些是系统(37)唯一的余维3 Hopf分支点。

由上述Lorenz系统结果还得到一些Chen和Lü系统Hopf分支的类似结果，不再赘述。与此同时，Wang等[73]利用奇点量方法研究Lorenz系统(37)在中心流形上的多重极限环分支和中心-焦点判定问题，给出定理41～44。

定理 41[73]Lorenz系统(37)在局部中心流形上的非平凡平衡点E±是中心当且仅当σ=1。

定理 42[73]Lorenz系统(37)的非平凡平衡点E±是3阶细焦点当且仅当ω=ω(k),σ=σ(k),k=1,2,

式中：

定理 43[73]假设定理42中条件成立，则在Lorenz系统(37)的单一非平凡平衡点附近可产生3个小振幅极限环，其中在特定条件下，可产生2个稳定极限环。

定理 44[73]在定理43条件下，Lorenz系统(37)的2个对称奇点E±经Hopf分支共可产生6个且至多6个小振幅极限环。

由以上结果可知，虽然这3个混沌系统(Lorenz、Chen和Lü系统)密切相关，但Lorenz系统在Hopf分支方面与Chen系统和Lü系统还有很大不同。

2018年，Huang等[74]考虑Lorenz系统(37)在σ≠0情形下的可积性问题，通过研究系统亚纯首次积分和形式首次积分的存在性，证明定理45、46。

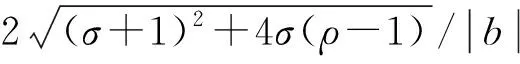
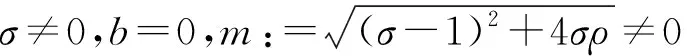
① 系统(37)在函数无关性意义下有且仅有一个形式首次积分;

② 若系统(37)有一个形如Φ(x,y,z)exp(-λt)的时变形式首次积分，则

③ 若系统(37)有一个形如Φ(x,y,z)exp(-λt)的时变形式首次积分，且(σ+1)/m∉Q,则存在正整数k∈N，使得λ=-k(σ+1)。

2007年，Li等[75]考虑广义Lorenz标准型

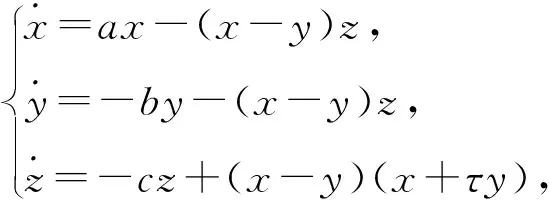
(40)

的Hopf分支问题，通过计算系统(40)在中心流形上的第一阶Lyapunov量，证明当a≠b时，系统奇点能分支出1个极限环，但细焦点阶数尚未确定，并且没有讨论a=b的情形。Liu等[76]2014年继续完善文献[75]中工作，对a≠b的情形，利用结式方法分解Lyapunov量中的代数变量，证明细焦点阶数为3；对a=b的情形，通过寻找系统(40)的一个不变曲面，证明系统的达布可积性。

对如下广义Lorenz系统

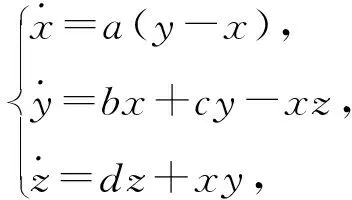
(41)

式中a、b、c、d是实参数。2012年，Wu等[77]描述了系统(41)的所有达布多项式和有理首次积分，其结论包括Lorenz系统(37)、Chen系统(38)和Lü系统(39)的情形。然而，Algaba等[78]2014年发现文献[77]的不足，主要提升了2方面的工作：一方面，当c≠0时，通过时间和坐标的线性缩放，证明广义Lorenz系统(41)和Lorenz系统(37)的等价性，从而得到相同结果，这一方法更加直接，避免文献[63]中复杂计算和推理；另一方面，当c=0时，找到系统(41)的一个新的达布多项式，这也是系统的一个首次积分，从而证明文献[77]中定理1.1和推论1.2是不正确的。另外，Algaba等[79]还考虑系统(41)在中心流形上的中心问题，证明当d=-2a,c=a,a(a+b)>0时，广义Lorenz系统(41)在解析的中心流形上有一个中心，并将这个结论分别运用到标准Lorenz、Chen和Lü系统，得到Lorenz系统(37)、Chen系统(38)和Lü系统(39)在解析中心流形上的中心条件分别为

b=-2,σ=-1,ρ<1;

B=2A,C=A,A≠0;

B=2A,C=A,A≠0。

2019年，Yu等[80]研究如下一类扩展Lorenz系统

(42)

在中心流形上的极限环分支问题。当am/(ap+rm)≥0，ap+rm≠0时，系统(42)有对称平衡点

作变换

系统(42)可转换为标准Lorenz系统(37)，但系统(37)和系统(42)不是拓扑等价的。文献[80]证明以下Hopf分支结果(定理47～49)。

定理 47[80]当a>0,m<0时，系统(42)在临界点n=0从原点E0能发生Hopf分支。当am>0,a+n>0时，在临界点p=pH从对称平衡点E±能发生Hopf分支。此外，不可能同时从原点E0和E±产生Hopf分支。

定理 48[80]当a>0,m<0时，系统(42)可在临界点n=nH=0从原点E0发生Hopf分支，且若r>0(r<0)，则Hopf分支是超临界的(亚临界的)，在原点E0附近产生一个稳定(不稳定)的极限环。在这种情况下，不能同时从E±发生Hopf分支。

定理 49[80]当am>0,a+n>0时，在临界点p=pH从对称平衡点E±能发生Hopf分支。在E+或E-附近的小极限环最大数目可达到3个，其中外部是一个稳定或不稳定的极限环。因此，从对称平衡点E±分支出的极限环最大总数为6。

另外，文献[80]还运用Matlab给出几个例子的数值模拟，以此说明理论结果的正确性。2019年，García等[81]研究Lorenz、Chen和Lü系统在中心流形上的中心环性数问题，证明以下极限环分支结果(定理50)。

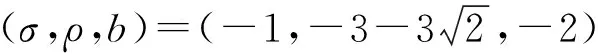
① 在保持奇点性质为Hopf点的族内扰动下，任何中心(原点或E±)的环性数为0；

② 在全族系统(37)内的扰动下，任何中心(原点或E±)的环性数为1。

基于定理50中Lorenz系统环性数结果，可以得到定理51。

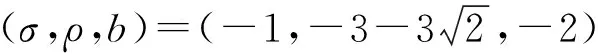
① 在保持奇点性质为Hopf点的族内扰动下，任何中心(原点或E±)的环性数为0；

② 在全族(38)和(39)内的扰动下，任何中心(原点或E±)的环性数为1。

4 三维分片光滑系统

分片光滑系统在机械、电子、力学和自动化工程中有大量应用，近些年对它的动力学行为，特别是极限环分支的研究已成热点。平面分片光滑系统极限环的研究已有大量结果，例如线性分片光滑系统有2个极限环[82]、3个极限环[83]；二次分片光滑系统有5个和8个极限环[84]；三次分片光滑系统分支出11个极限环[85]、18 个极限环[86-87]、n次扰动分支出极限环[88]等。平面、三维甚至更高维分片光滑系统都有比对应的光滑系统更复杂的动力学行为。就分支问题而言，它不是光滑系统分支的简单推广，还会出现一些新的分支，如非光滑Hopf分支、C-分支、边界碰撞分支等，所以分片光滑系统的分支问题比光滑系统更具有挑战性。近年来一些学者开始探索三维分片光滑系统的分支问题，特别是极限环分支问题，但这方面的文献还很少，下面介绍部分相关成果。

2005年，Freire等[89]研究如下三维分片光滑线性系统的极限环分支问题

(43)

式中：x∈R3，L、C和R分别表示R3在x1<-1、|x1|≤1、x1>1的区域。在可观测性的一般条件下，每个系统(43)都可以写成如下广义Liénard形式

(44)

式中sat(x1)=sign(x1)·min{|x1|,1}是标准饱和度，使系统(43)中

选择T为分支参数，对临界值Tc=D/M,M>0，系统(43)在C区域有一个线性中心，即矩阵AC有一对纯虚特征值。通过分析分支参数，得到以下极限环存在的判据(定理52)。

定理 52[89]考虑具有M>0,Tc=D/M,γ=DM-Dm+dM-tM2≠0的系统(44)。对T=Tc，系统发生焦点-中心-极限环分支，也就是说，对T=Tc，在C区域存在线性中心构形，使得当γ(T-Tc)>0且T-Tc足够小时，从线性中心产生一个极限环。

定理52的结果被用于准确预测与经典Van der Pol振荡器相关的三维电子电路中对称周期振荡的产生。同一时间，Carmona等[90]考虑具有2个区域的三维连续分片线性系统的极限环分支问题，获得与定理52类似的结果，证明有界线性中心构形中切于分离面的周期轨道产生一个极限环。文献[90]还将所得结果应用于Chua振荡器非对称周期振荡的研究。接着，Freire等[91]2007年考虑文献[90]所研究系统的一种退化分支情形，证明在一定参数条件下，该系统最多产生2个极限环，且在Chua电路中解释了这一结论的合理性。2013年，Ponce等[92]考虑三维对称分片光滑线性系统(44)的fold-Hopf分支，证明该系统可同时分支出3个极限环，且给出了判定这些极限环的稳定性条件。另外，文献[92]还将获得的理论结果应用于一个广义Chua电路系统中。

关于线性控制系统的极限环，2004年，Moreno等[93]研究如下闭环稳定系统

(45)

式中u=(1+λ3)x1+3(1-λ2)x2+3(1+λ)x3,λ<0。这是一个三维分片光滑线性控制系统。文献[93]严格证明了对于参数λ的唯一固定值，系统(45)在原点共存着一个稳定极限环与一个稳定平衡点。后来Ponce等[94]2009年通过数值计算，表明在λ的2个数值区间，系统(45)有2个极限环，其中一个是稳定的极限环。Llibre等[95]2011年研究一类三维分片光滑线性控制系统的极限环问题，运用代数方法确定了该类系统的极限环个数。

最近，Freire等[96]研究如下三维分片光滑线性系统在无穷远点在不变曲面上的极限环问题

(46)

式中x<0；且

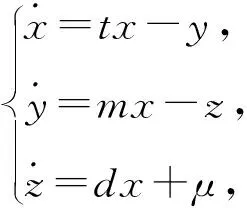
(47)

其中x>0。运用平均理论分别讨论系统(46)、(47)在半齐次和非齐次情形下的极限环分支问题，同时给出了系统(46)和(47)的一个特例，证明从无穷远点的中心能分支出1个极限环的结论。另外，该团队还在文献[97]中类似考虑一个三维对称分片光滑线性系统在无穷远点的Hopf分支，运用闭合方程法给出系统在无穷远点的大振幅极限环的存在性及稳定性判据。作为方法的应用，研究Bonhoeffer-van der Pol oscillator振荡器中大振幅极限环的分支问题。

5 结语

本文综述三维微分系统的极限环分支与等时中心的一些相关研究进展。

在研究的系统方面，目前主要集中于包括三维LV系统、Lorenz系统族等的三维多项式光滑系统，以及三维分片光滑系统。所研究的光滑系统大多数是三维二次系统，这主要是由于研究极限环与等时中心的过程中涉及到大量符号计算，随着系统参数的增多和次数的升高，对计算机软、硬件的要求更高，一般三维高次系统往往会出现超出计算机代数系统计算能力的情况。

在研究方法方面，研究极限环的方法主要有Poincaré-Bendixson环域定理、Hopf分支(多重Hopf分支)方法、Melnikov函数方法以及平均值方法。而等时中心的研究主要是求系统中心点的周期常数，计算周期常数的常用方法有从周期函数T(h)的展开式中求出hk的系数直接方法[98]、规范形方法[99]与复系统方法[7,13,100]。以上方法各有优势，规范形方法通过变换减少系统参数，从而降低计算复杂性，但寻找合适的变换是难点；Melnikov函数方法需要进行大量积分运算；复系统方法将系统转换到复数域中，运用递推公式进行计算，避免复杂的积分运算和解方程。在研究中首先要解决的关键问题是寻找系统的不变代数曲面或中心流形，这在理论分析和计算上都非常困难，而且没有一般快捷的方法。有些算法虽然可以省略直接求中心流形，但在证明等时中心的充分性时还是需要求出相对简单可用的中心流形，这就是三维微分系统等时中心研究结果偏少的原因。

近几十年才开始探索三维微分系统的极限环分支和等时中心，特别地，三维系统的等时中心研究才刚开始起步，这些问题的研究在理论和应用上都有重要意义。随着计算机符号计算系统的发展与应用，国内外学者解决了一些特殊三维微分系统的极限环和等时中心问题。但是还有很多问题待研究，例如，类比平面二次系统已经解决的小振幅极限环问题(环性数)、中心与等时中心问题、三维二次系统都是开放问题。因此，相关定性分析方法和计算方法都需要有突破。另外，三维三次、四次、五次齐次系统的Hopf分支、中心与等时中心也是可进一步研究的问题。三维微分系统的临界周期分支问题也值得研究。