有限群不可约特征标的余次数
卢家宽, 王 宇, 张博儒, 庞琳娜
(广西师范大学 数学与统计学院, 广西 桂林 541006)
设G是有限群,Irr(G)表示群G的全体不可约复特征标组成的集合,cd(G)={χ(1)|χ∈Irr(G)}。集合cd(G)与群G之间的联系已经被广泛研究,取得了相当丰富的成果,并且新成果仍在不断涌现中,读者可参见Isaacs[1]的专著《有限群的特征标理论》第12章、Berkovich等[2-3]的专著《有限群的特征标理论》,以及Isaacs[4]最近出版的专著《可解群的特征标理论》。Qian等[5]定义了不可约复特征标的余次数。
定义 1[5]设χ∈Irr(G),令
称cod(χ)为χ的余次数。群G的全体不可约复特征标余次数组成的集合记为cod(G), 即cod(G)={cod(χ)|χ∈Irr(G)}。
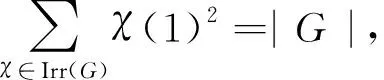
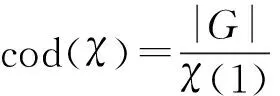
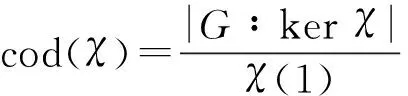
下面是关于特征标余次数最基本的性质,可以保证有效使用归纳法, 便于开展深入研究。
引理 1[5]设χ∈Irr(G),则
① 若N是G的正规子群,满足N≤kerχ,则χ在G/N中的余次数与在G中的次数相等;

不可约特征标的余次数最近10多年被越来越多的学者关注,从多方面开展研究, 取得了不少成果。下面从余次数的算术条件对有限群结构的影响、余次数与其他算术量之间的联系等方面综述该领域的相关研究成果。本文只涉及有限群,采用的符号参看文献[1]。
1 余次数的算术条件对有限群结构的影响
与特征标次数类似, 特征标余次数的算术性质也能提供有限群的结构信息。例如,1999年Gagola等[13]证明了定理1。
定理1[13]设G是有限群,则G是幂零群当且仅当对每个χ∈Irr(G),有χ(1)|cod(χ)。
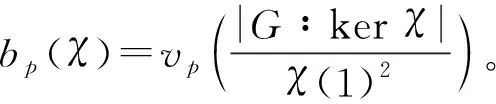
定理2[14]设G是有限群,p是素数。若对每个χ∈Irr(G),当p整除χ(1)时, 都有bp(χ)≥0,则下列结论之一成立:
①G是p-闭的;
②p=2,G有合成因子A7;
③p=3,G有合成因子A7、A11、A13、M22之一。
若正整数m整除|G|,且gcd(m,|G|/m)=1,则称m为群G的Hall-数。2007年,Liang等[15]对每个χ∈Irr(G),χ(1)都是Hall-数的有限群进行分类。设χ∈Irr(G), 若χ(1)是G/kerχ的Hall-数, 则称χ为G的Hall-特征标。2016年,Liang等[16]对每个χ∈Irr(G)都是Hall-特征标的有限群进行分类。为节约篇幅,这里略去这两类群的结构。
上述定理1也可以叙述为:有限群G是幂零群当且仅当对每个χ∈Irr(G),有cod(χ)=αχχ(1),这里αχ是正整数。2000年, Berkovich[17]证明一个强化版的定理1。
定理3[17]设G是有限非交换群,则G是p-群当且仅当对每个χ∈Irr(G), 有cod(χ)=psχχ(1),这里sχ是与χ有关的正整数。
2020年,Yang等[18]给出了G可解的一个充分条件。
定理4[18]设G是有限群,若对每个χ∈Irr(G),有cod(χ)≤pχχ(1),则G可解,这里pχ是|G∶kerχ|的最大素因子。
最近,Gao等[19]又给出了G可解的一个充分条件。
定理5[19]设G是有限群,若对每个χ∈Irr(G),有cod(χ)≤χ(1)α,则G可解,这里α≈1.887 6。
Berkovich证明定理3只使用了正规子群的特征标理论, 而上述可解群的2个充分条件(定理4、5),都是通过单群分类定理分析而得到。
在研究特征标余次数的算术条件对有限群结构的影响时,人们主要考虑与特征标次数相对应的问题。因此,为便于对比,有时候同时列举特征标次数和余次数的相关结果。
在特征标次数的研究中,有以下2个著名定理(定理6、7)。
定理6[20](Thompson定理) 设G是有限群,若对每个χ∈Irr(G),有p|χ(1),则G有正规p-补。

定理6、7被广泛研究和推广,这里不再赘述。本文主要关心特征标余次数版的相关结论。
首先,2007年Qian等[5]证明了以下定理8。

最近,Chen等[22-23]得到以下定理9。

定理9中p-可解的条件是不可缺少的。Chen等[23]对定理9做了一些推广。
设H是G的极大子群,若χ∈Irr(G)是(1H)G的不可约组成,则χ为相对于H的P- 特征标。G的所有P- 特征标组成的集合记为IrrP(G)。Qian等[24]首先研究P- 特征标对群结构的影响,得到了许多有趣的结果。Lu等[25]使用P- 特征标给出G有正规p-补的一个充分条件。

关于Ito-Michler定理的余次数版相关结论,Bahramian等[26]证明了定理11。
定理11[26]设G是p-可解群,素数p不等2,也不是梅森素数,则对每个1G≠χ∈Irr(G),p|cod(χ)当且仅当G是p-群。
记
ep(G)=max{logp(χ(1))p|χ∈Irr(G)},
cp(G)=max{logp(cod(χ))p|χ∈Irr(G)},
则著名的Ito-Michler定理可以表述为:ep(G)=0当且仅当G有交换正规Sylowp-子群。文献[27-29]已经证明:当ep(G)≤1时,有|G∶Op(G)|p≤p3。
Qian等[5]证明:只要p整除|G|,则cp(G)≥1。因此,cp(G)=0当且仅当G是p′-群。Bahramian等[30]证明了定理12。
定理12[30]设G是非p-可解群,且cp(G)≤1,则|G|p=p。
因此,当cp(G)≤1时,G有初等交换的Sylowp-子群。
Qian等[31]给出当cp(G)≤1时有限群G的特征性质。

①P∈Sylp(G)初等交换,V=Op′p(G)是p′-群;
② 把P看作p元域上的线性空间,则H/CH(P)≤Z(GL(P)),这里H∈Hallp′(G/V);
③V可解,且CV(P)=1;

对|cd(G)|较小的有限群,已经有较多研究,可参见Isaacs[1]的专著《有限群的特征标理论》第12章。例如,如果|cd(G)|≤3,那么G是可解群; Noritzsch[32]给出了满足|cd(G)|=3的若干群类的结构;Malle等[33]则分类了满足|cd(G)|=3的非可解群。
2016年,Du等[34]证明:满足|cod(G)|=2的p-群是初等交换的, 满足|cod(G)|=3的p-群G的幂零类长c(G)至多为2。文献[34]还提出以下问题:一般情况下,是否可以使用|cod(G)|来给出p-群G幂零类长c(G)的上界。
2019年,Alizadeh等[35]继续研究|cod(G)|较小的有限群,得到如下定理14、15。
定理14[35]设G是有限群,则|cod(G)|=2当且仅当G是初等交换群。
定理15[35]设G是有限群,则|cod(G)|=3当且仅当G是可解群且满足下列条件之一:
①G是幂零类为2的p-群,且cod(G)={1,p,ps},其中s≥2;
②G是pn(pn-1)阶Frobenius群,其中Frobenius补是p阶循环群,π(G)={p,q},cod(G)={1,p,ps},其中s≥1。
2020年,Croome等[36]继续讨论|cod(G)|=4的p-群,得到许多有趣的结果。特别地,在附加一些条件下,部分回答了Du等[34]的上述问题。
定理16[36]设G是有限p-群,且cod(G)={1,p,pb,pa},其中2≤b ① |cd(G)|=2; ② cod(G)={1,p,q2}; ③ |G∶G′|=p2, 则G的幂零类长c(G)至多为4。 幂零类长的更多上界参见文献[37]。最近, Moretó[38]证明:一般情况下,可以使用|cd(G)|和|cod(G)|来给出p-群G幂零类长c(G)的上界。 定理17[38]设G是非交换p-群,则 c(G)≤(|cod(G)|-2)(|cd(G)|-1)+1。 设G是pn阶p-群,且c(G)=c,则cc(G)=n-c称为G的余类长。 定理18[38]设G是p-群,|cod(G)|=4且cc(G)=m,则c(G)≤m+3。 特征标理论研究中有个著名的Taketa猜想:如果G是可解群,那么G的导列长dl(G)≤|cd(G)|。该猜想也称为Taketa不等式,已经有不少研究,这里不再赘述。自然可以提余次数版的Taketa问题:如果G是可解群,那么G的导列长dl(G)≤|cod(G)|。 Liu等[39]考虑|cod(G)|=4、5的非可解群,得到定理19、20。 定理19[39]设G是满足|cod(G)|=4的非可解群,则G同构于L2(2f),其中f≥2。 定理20[40]设G是满足|cod(G)|=5的非可解群,则G有唯一非平凡正规子群M,使得|M|=22f,G/M≅L2(2f),并且M的所有非平凡元素构成G的一个共轭类,每个非平凡λ∈Irr(G)的稳定子群是G的Sylow 2-子群, 或者G同构于L2(q), 其中q=rf>5,r是奇素数。 令Irr1(G)为群G的全体非线性不可约复特征标组成的集合,cd1(G)={χ(1)|χ∈Irr1(G)}。若存在正整数n,使得|cd1(G)|=|Irr1(G)|-n,则称G为Dn-群。易见,D0-群就是不同非线性不可约特征标有不同次数的有限群。1992年,Berkovich等[41]确定了D0-群的结构。 定理21[41]设G是D0-群,则G是下列群之一: ①G是超特殊2-群; ②G是pn(pn-1)阶Frobenius群,其中 Frobenius核的阶是pn,Frobenius补循环; ③G是72阶 Frobenius群,其中Frobenius补同构于8阶四元素群。 相应地, 若存在正整数n, 使得|cod(G)|=|Irr(G)|-n, 则称G为D′n-群。易见,D′0-群就是不同不可约特征标有不同余次数的有限群。最近,Ebrahimi[42]发现这样的群的结构很简单。 定理22[42]有限群G是D′0-群当且仅当G同构于Z2或S3。 由此可见,D′0-群的结构比D0-群简单。Berkovich等[43-44]分类了D1-群。因此,考虑D′1-群的结构也是有意义的问题。Berkovich在其特征标理论专著中提出如下问题: 问题1[2]设G是有限群,对每个非线性χ∈Irr(G),cod(χ)是素数, 则G的结构如何? 2016年,Xiong[45]解决了上述问题。 定理23[45]设G是有限群,对每个非线性χ∈Irr(G),cod(χ)是素数,则G是下列群之一: ① 2阶或3阶循环群; ② 交错群A4; ③ 对称群S3; ④ 10阶二面体群D10; ⑤ 21阶非交换群。 也有学者从cod(χ)的素因子个数或公因子等情况入手,研究G的结构。例如,2020年Sayanjali等[46]证明了定理24。 定理24[46]若对任意1≠d∈cod(G),都有|π(d)|=2,则G/N≅L2(q),其中q∈{5,7,8,9,17},N是G的可解剩余。 最近,Alizadeh[47]证明了定理25。 定理25[47]设G的所有不可约特征标余次数中只有一个是合数,则G是可解群,且|cod(G)|≤5。 设N是有限群G的非平凡正规子群,记Irr(G|N)=Irr(G)-Irr(G/N)。2021年, Ahanjideh[48]证明了定理26。 定理26[48]设N是G的非平凡正规子群,若对任意χ≠ψ∈Irr(G|N),都有χ(1)和ψ(1)的最大公因子为1或为素数,则N是可解群。 本章主要综述特征标余次数自身的性质以及特征标余次数与元素的阶等其他算术量之间的联系。 2011年,Qian[49]首先证明了如下定理27、28。 定理27[49]设G是可解群,g∈G, 则存在χ∈Irr(G), 使得kerχ∩〈g〉=1, 并且对o(g)的每个素数因子p,有p|cod(χ)。 定理28[49]设G是可解群,g∈G有素数幂阶,则存在χ∈Irr(G),使kerχ∩〈g〉=1,且o(g)|cod(χ)。 随后,Isaacs[50]使用有理特征标理论,证明定理27对所有有限群成立。 定理29[50]设G是群,g∈G,则存在χ∈Irr(G),使得kerχ∩〈g〉=1,并且对o(g)的每个素数因子p,有p|cod(χ)。 最近,Qian[51]证明了定理28的加强版。 定理30[51]设G是可解群,g∈G,则存在χ∈Irr(G),使得o(g)|cod(χ)。 Qian在文献[51]也验证了定理30的结论对部分单群和非可解群也成立, 但对所有有限群是否成立,仍是未解决的问题。 设G是p-可解群,记G的p-长为lp(G),即G的每个因子都是p-群或p-群的正规列中p-因子最小可能的个数。记 codp(G)={cod(χ)|χ∈Irr(G),p|cod(χ)}。 2020年,Grittini[52]给出了p-长lp(G)的一个上界。 定理31[52]设G是p-可解群,则lp(G)≤|cdp′(G)|。 2021年,Ahanjideh[53]给出了p-长lp(G)的余次数版的上界。 定理32[53]设G是p-可解群,则lp(G)≤|codp(G)|。 于是,自然可以问lp(G)是否可以达到上述2个上界,当达到上界时,G的结构是什么。 Ahanjideh[53]还证明了定理33。 定理33[53]设素数p整除G的阶,codp(G)={m}, 这里m是某个正整数, 则G是p-可解群,且lp(G)=1。 最近, Bahramian等[30]继续使用特征标余次数讨论lp(G)的上界。 记 σ(G)=max{π(χ(1))|χ∈Irr(G)}。 ρ(G)={p是素数|存在χ∈Irr(G),使得p整除χ(1)}。 Huppert猜想可以使用ρ(G)描述|σ(G)|的上界,把该猜想称为ρ-σ猜想。ρ-σ猜想是特征标理论中的著名公开问题,该猜想已有许多研究,这里仅列举关于特征标余次数版的ρ-σ猜想的研究进展。令 σ(cod(G))=max{|π(cod(χ))||χ∈Irr(G)}, ρ(cod(G))={p是素数|存在χ∈Irr(G),使得p|cod(χ)}。 文献[5]提出如下问题2。 问题2[5]对有限群G,是否存在常数k,使得|ρ(cod(G))|≤kσ(cod(G))?特别地,当σ(cod(G))=2时,是否有|ρ(cod(G))|=4? 2017年,Yang等[54]给出了问题2前半部分的肯定回答。最近, Moretó[55]给出了问题2后半部分否定的回答,特别地,文献[55]提出如下问题3。 问题3[55]设G是有限可解群,χ∈Irr(G),是否存在g∈G,使得π(cod(χ))⊂π(o(g))? 问题3似乎可以看作定理30的逆命题。最近,Jin等[56]给出该问题的否定回答。特别地,他们证明了定理35。 定理35[56]设G是可解群,χ∈Irr(G)是忠实本原特征标,则π(cod(χ))=π(G)。 1990年,Huppert还提出另外一个猜想:设H是非交换单群,若G是有限群,满足cd(G)=cd(H),则G≅H×A,这里A是交换群。 该猜想已有许多研究。2021年,Bahri等[57]提出余次数版的Huppert猜想, 即: 设H是非交换单群, 若G是有限群, 满足cod(G)=cod(H), 则G≅H×A, 这里A是交换群。 定理36[57]设G是有限群, 满足cod(G)=cod(PSL(2,q)), 则G≅PSL(2,q)。2 余次数与其他算术量之间的联系



