基于几何非线性圆拱动力模型的拱形温室自振周期分析

张焱辉 李百丰 邓 婷,2 韩盛柏,3 蒋秀根*

(1.中国农业大学 水利与土木工程学院,北京 100083;2.唐山市住房和城乡建设局,河北 唐山 063000;3.中国建筑科学研究院有限公司 建研科技股份有限公司,北京100013)

拱形温室是设施农业中常用的温室型式,其内部空间大,受力具有优越性,非常适合规模化作业[1]。拱形温室结构较轻,跨度较大,一般采用柔长细薄的杆件作为骨架,结构外覆盖柔性薄膜,使得这种结构对风荷载较为敏感,风荷载对结构产生的动力响应是温室结构设计中需要重点考虑的问题之一[2-3]。并且,风振中风荷载的计算非常复杂,结构在风荷载作用下的内力和变形也非常复杂。因此研究拱形温室自振特性,提高结构抗风与抗撞击性能,保证温室结构设计的安全性,具有重要的科学意义。

拱作为一种压弯结构,由于轴线曲率的影响,截面存在压弯二重耦合[4]:一是拱轴线曲率产生的耦合,轴线曲率导致拱的轴向变形和弯曲变形相互耦合,增大了二者在求解过程中的难度;二是大挠度产生的二阶弯矩,在拱结构中,截面的轴力与弯矩相互耦合,使得拱结构以受压为主,轴向压力对截面产生的二阶效应不可忽略。同时,拱形温室结构由于其截面整体抗弯刚度不足,容易引起较大的截面转动,以及温室拱结构的薄腹结构型式容易引起较大的剪切变形,使得在研究温室结构的弯曲自振特性时,需要引入考虑剪切变形的Timoshenko梁理论[5]。另外,拱的振动问题还需要考虑惯性力的影响[6],结构的振动会产生平动惯性力和转动惯性力,二者直接作用在结构上,使结构的受力分析变得更为复杂,尤其是转动惯量的影响会使拱结构的振动特性与仅考虑平动惯量的拱结构振动特性有较大区别。

目前,国内外在温室结构力学性能方面的研究较多。如考虑材料几何非线性以及弹塑性时温室结构的最不利位置[7],温室结构在荷载作用下内力以及变形的计算方法[8-10]、温室结构产生的变形量计算问题[11-12],对拱形温室的纵向抗风性能进行分析,建立以矩阵形式表达的刚度平衡方程[13]。但关于温室结构动力响应问题的研究较少。李成志等[14]用有限元法对异性温室结构进行了静力线性分析,雷隽卿等[15]利用有限元软件ANSYS,对脉动风下考虑流固耦合的温室结构进行了数值模拟计算和分析,但仅对温室结构的矩形框架部分进行了研究。邓婷等[16]对风振分析中的压杆弯曲振动的动态刚度矩阵模型理论进行研究,但仅考虑了平动惯性力,转动惯性力并未考虑,其研究对象也仅为温室杆件中的压杆。姜迎春等[17]等对考虑脉动风速的平面刚架日光温室结构动力响应规律进行了研究,对温室骨架结构动力响应进行时程分析,确定了骨架结构危险截面的位置,但并未考虑轴力对弯曲振动的影响。

本研究拟针对拱形温室的弯曲振动问题,考虑拱的弯曲变形、剪切变形、轴向压缩变形、二阶效应以及基于分布质量的平动惯性力和转动惯性力,采用直接刚度法,推导拱的动力模型,计算拱形温室不同模型的自振周期,分析其动力响应规律,以期为温室结构的动力分析和设计提供参考依据。

1 基本模型

1.1 基本假定

对温室结构中的圆拱杆件,按照右手螺旋法则定义坐标系(图1):以圆拱左端为坐标原点;以杆件轴线为x轴,向右为正;y轴垂直于曲轴平面,法向向上为正;z轴在曲轴平面内,垂直于杆件轴线,指向圆心O为正。

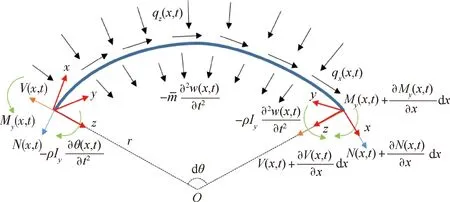
dθ为微段圆心角;r为圆拱半径;为平动惯性力;为转动惯性力矩。dθ are Micro-segment center angle. r are round arch radius. are rotational inertia moment.图1 圆拱杆件坐标系及受力分析Fig.1 Coordinate system and stress analysis of circular arch

杆件所受外荷载包括轴向均布荷载qx(x,t)、 径向均布荷载qz(x,t)、 均布力矩my(x,t), 所有外荷载与坐标轴方向一致为正;内力包括轴力N(x,t)、 剪力V(x,t) 和弯矩My(x,t), 当截面外法线方向与坐标轴正向一致时,内力与坐标方向一致为正,当截面外法线方向与坐标轴正向相反时,内力与坐标方向相反为正;位移包括轴向位移u(x,t)、 径向挠度w(x,t) 和截面转角θ(x,t), 位移与坐标轴方向一致为正。

本研究模型推导过程基于以下假定:等曲率拱,即圆拱,圆心角α=l/r, 其中r为圆拱半径,l为弧长;压弯耦合,考虑拱的拉压和弯曲变形相互影响;Timoshenko弯曲模型,采用平截面假定,考虑圆拱的剪切变形,截面法向与轴线不重合;大挠度模型,考虑压杆的二阶效应,即轴力在挠度上对截面产生的二阶弯矩;可压缩模型,考虑圆拱截面轴向刚度和轴向变形;等截面,截面质量与刚度保持常数;线弹性,材料应力与应变服从比例关系;准常轴力,在考虑二阶弯矩时,轴力视为常数,并且N0取压为正;弯曲振动,只考虑径向挠度运动产生的惯性力。

1.2 基本方程

1.2.1 平衡方程

对微段隔离体进行平衡分析,建立平衡方程,平衡方程包括轴力平衡方程、剪力平衡方程以及弯矩平衡方程,分别如下:

(1)

(2)

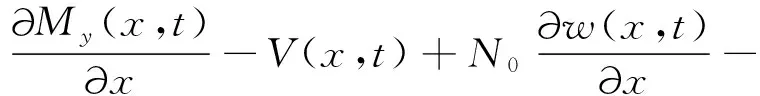
(3)

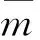
1.2.2 几何方程

几何方程为:

(4)

(5)

(6)

式中:εx(x,t)为轴向应变;γ(x,t)为剪切转角;κy(x,t)为法向弯曲曲率。

1.2.3 物理方程

物理方程为:

(7)

式中:E为弹性模量;A为截面面积;G为剪切模量;μ为截面剪应力不均匀系数。

1.3 位移控制方程及求解

将基本方程(1),(2),…,(7)中的荷载、位移以及内力采用分离变量法进行分解,公式为:

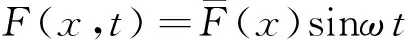
(8)

式中:ω为杆件弯曲振动圆频率。

1.3.1 位移控制方程

综合方程(1),(2),…,(8)得到径向挠度控制方程为:

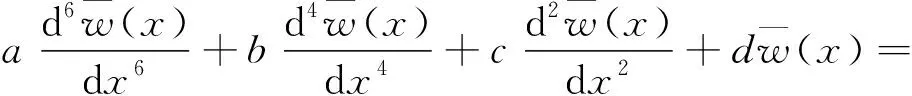
(9)

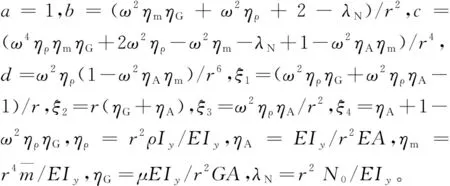
轴向位移控制方程为:

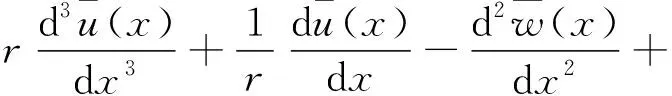
(10)

剪切转角控制方程为:

(11)

截面转角控制方程为:

(12)

1.3.2 挠度方程求解

根据方程(9)的齐次格式可得圆拱径向挠度通解一般格式为:

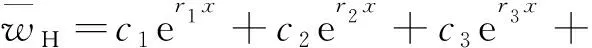
(13)

式中:c1,c2,…,c6为位移常系数;r1,r2,…,r6为特征根,特征根存在实根、虚根、零根及重根等情况,不同特征根对应不同的解。根据特征根的类型,解得径向挠度通解共有40种。本研究使用2种通解。

通解1:

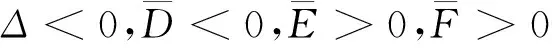
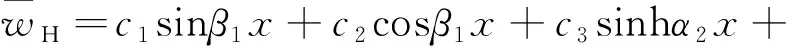
(14)

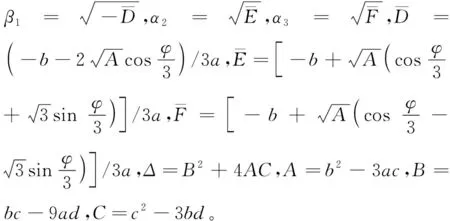
通解2:

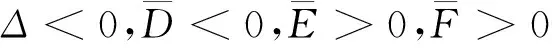
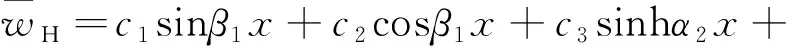
(15)

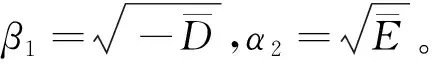
将通解(14)和(15)写为向量格式:

(16)

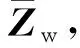
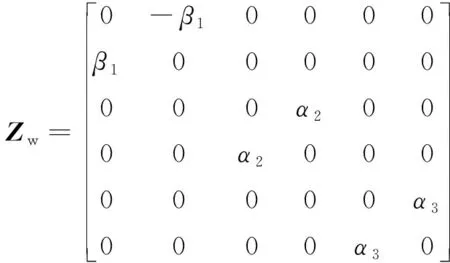
1.4 位移与内力

以径向挠度基函数为基础,结合基本方程以及位移控制方程,得到其他物理量的表达式和基函数见表1。

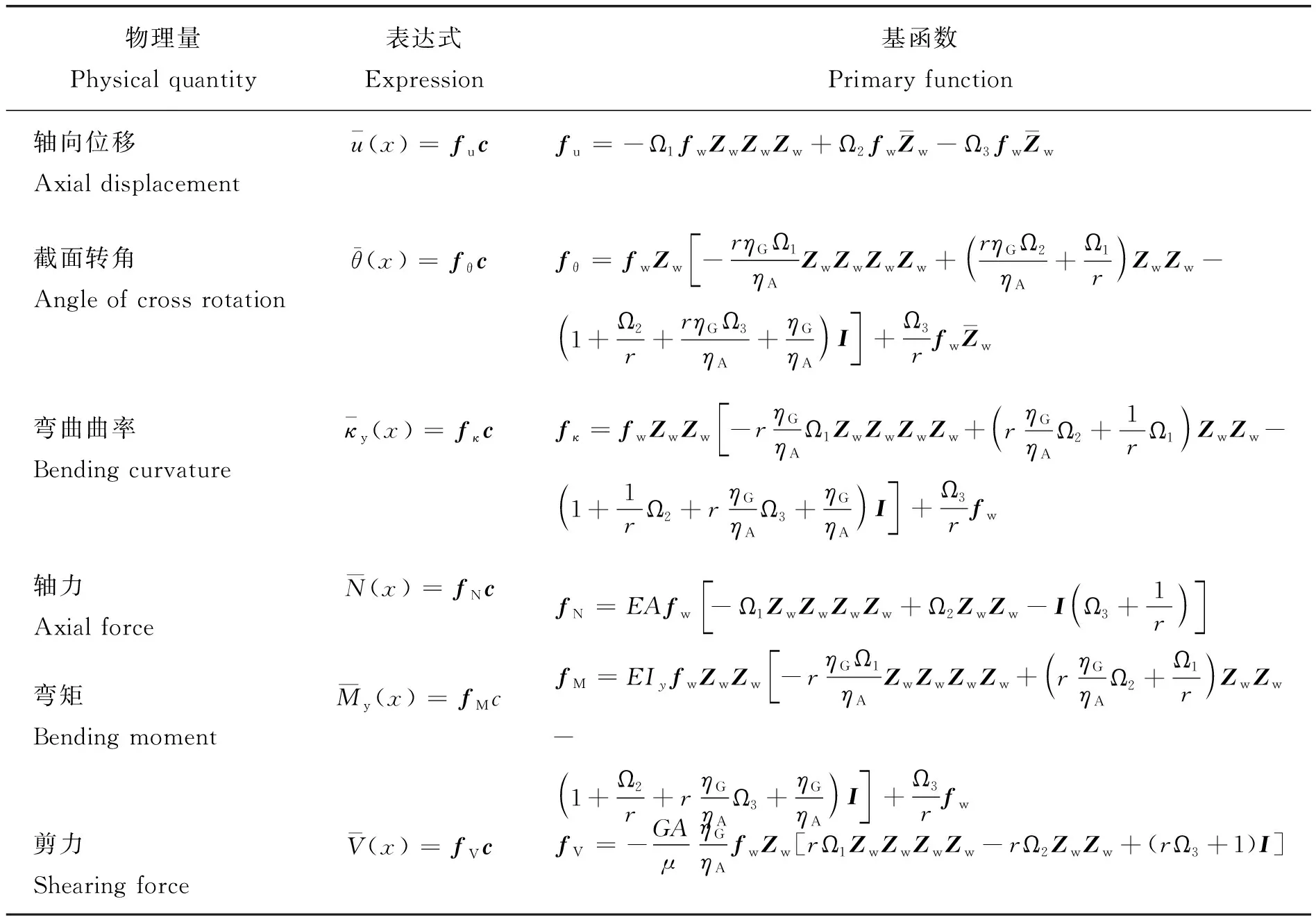
表1 其他物理量表达式及基函数Table 1 Other physical expressions and basis functions

2 自振分析方法

2.1 拱棚

拱棚结构形式简单,仅由1个圆拱构成,两端支座为铰支,根据边界条件,可得定解条件如下:左支座:径向挠度为0,即w(0)=0,轴向位移为0,即u(0)=0,曲率为0,即κy(0)=0;右支座:径向挠度为0,即w(α)=0,轴向位移为0,即u(α)=0,曲率为0,即κy(α)=0。根据定解条件,构建定解方程:

(17)

系数矩阵A中只有1个未知量ω,已知方程(17)一定存在有意义的非零解,则系数矩阵A需要满足特征方程:

|A|=0

(18)

通过求解方程(18),可以得到自振圆频率ω,进而由T=2π/ω得到结构的自振周期T。再将求得的ω带回系数矩阵A,通过求解方程组(17),得到位移系数c,再根据式(16),即可得到各阶振型。

2.2 典型拱形温室

采用本研究模型计算结构的自振周期时,首先需明确杆件边界条件。本研究中,将典型拱形温室结构抽象为3个杆件,两端支座铰接,拱与柱子刚接,其结构示意见图2。由边界条件和连续条件得该温室结构定解条件见表2。

底部柱子为一般动力梁,其位移与内力根据文献[18]得到。由表2的定解条件可以得到系数矩阵A,由特征方程|A|=0可以求得结构自振周期,再由Ac=0,可以求得位移系数c,最后根据式(16),即可得到各阶振型。

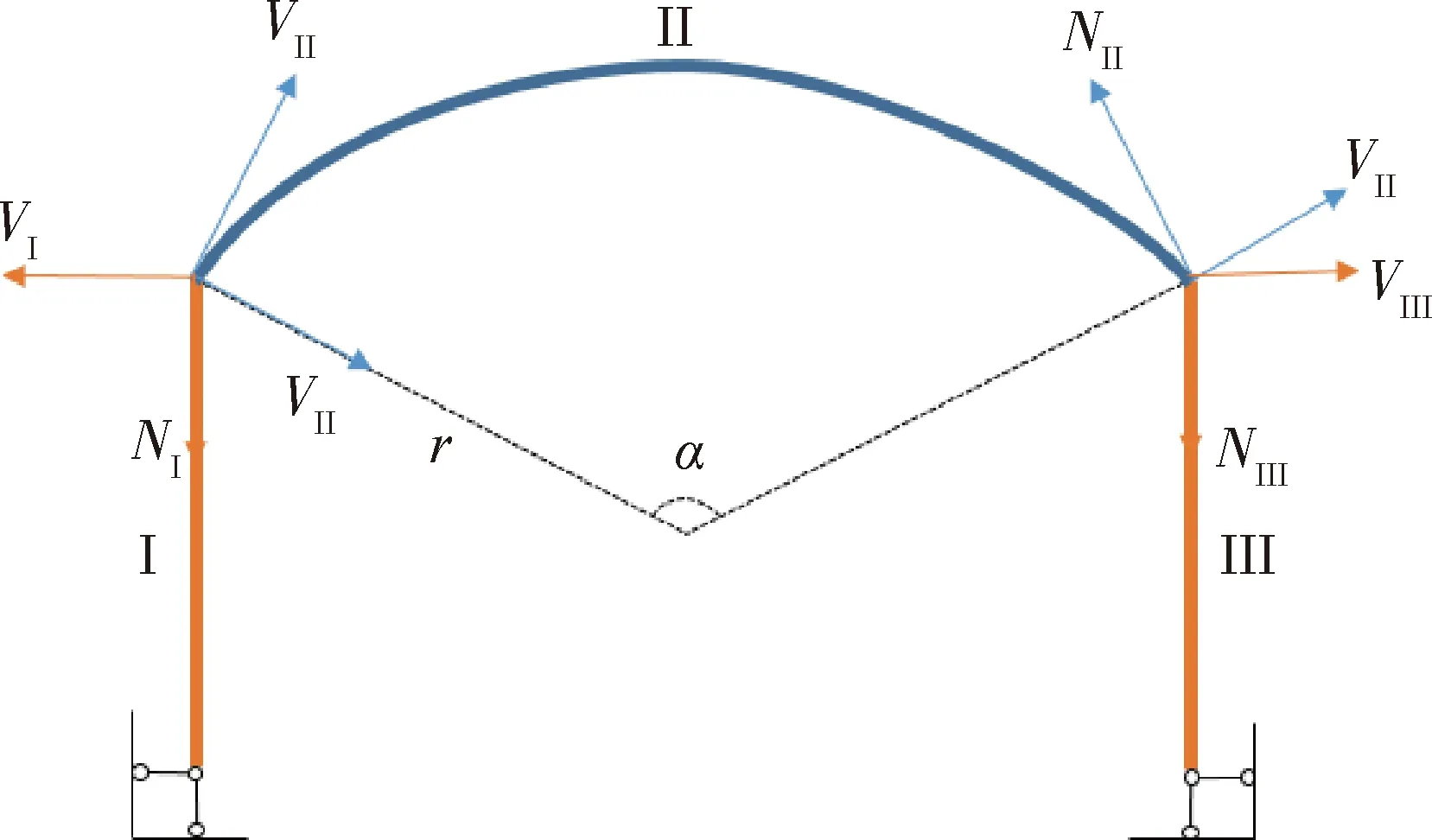
I、II、III为杆件编号。VI、VII、VIII分别为杆件I、II、III的剪力;NI、NII、NIII分别为杆件I、II、III的轴力。r为圆拱半径;α为圆心角。I, II and III are bar numbers. VI, VII and VIII are shear force of bars I, II and III; NI, NII and NIII are axial forces of bars I, II and III. r is round arch radius; α is central angle.图2 典型拱形温室结构示意图Fig.2 Typical arched greenhouse structure diagram

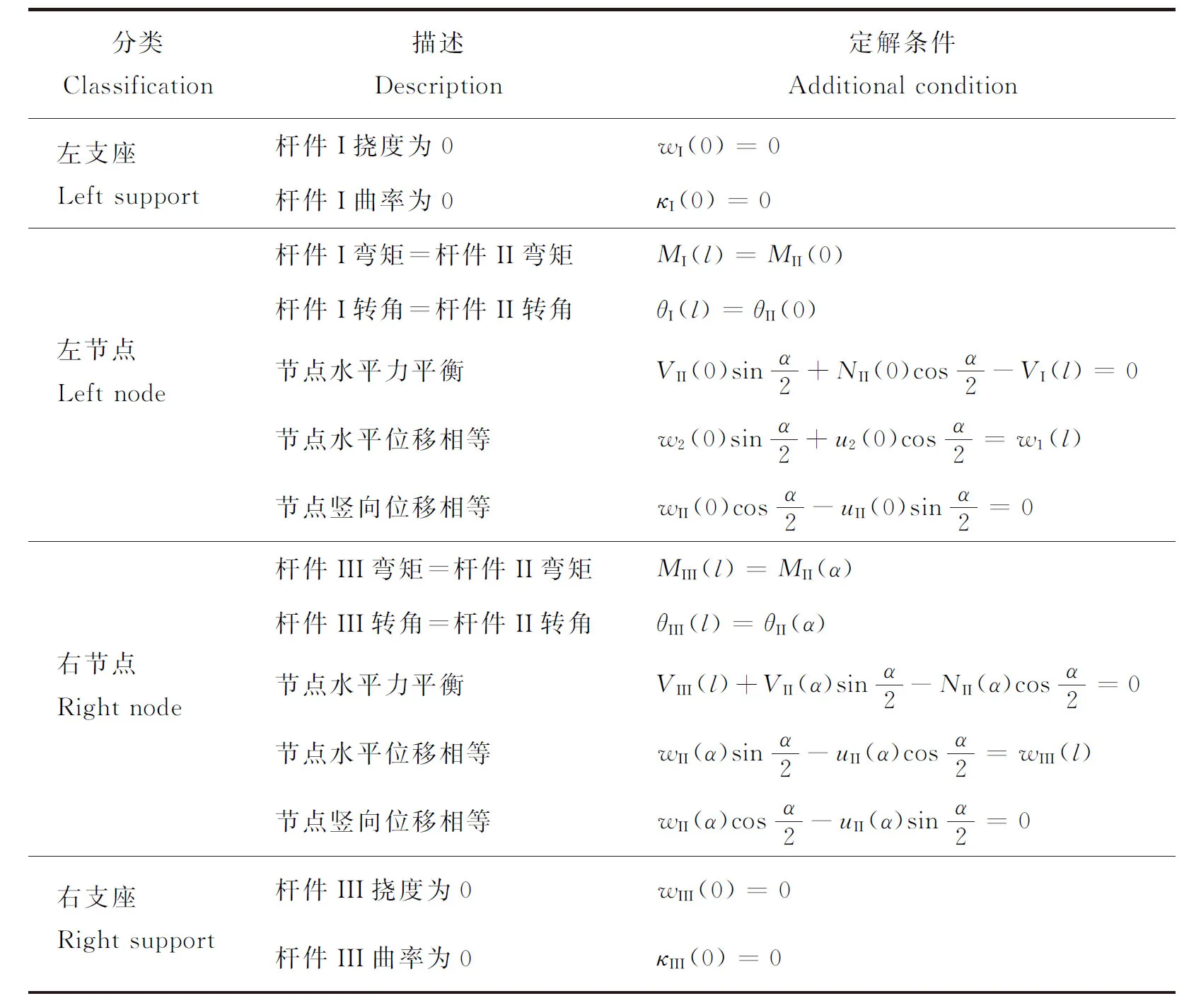
表2 典型拱形温室结构定解条件Table 2 Solution conditions of typical arched greenhouse structure

3 拱形温室结构自振周期计算

在计算拱形温室自振周期时,共考虑了以下8种不同的模型:

模型1,几何线性不可压缩平动Euler梁模型;

模型2,几何线性不可压缩平转动Euler梁模型;

模型3,几何线性不可压缩平转动Timoshenko梁模型;

模型4,为几何线性可压缩平转动Euler梁模型;

模型5,几何线性可压缩平转动Timoshenko梁模型;

模型6,几何非线性可压缩平动Euler梁模型(N0=0.3Ncr);

模型7,几何非线性可压缩平转动Euler梁模型(N0=0.3Ncr);

模型8,几何非线性可压缩平转动Euler梁模型(N0=0.5Ncr)。

3.1 拱棚

选取跨度为8 m,失高为3 m的拱棚,用本研究模型计算其自振周期。杆件为焊接薄壁圆钢管,截面规格为Φ51×2 mm,所用材料弹性模量E=2.06×105MPa,剪切模量G=8.0×104MPa,剪应力不均匀系数μ=1.2,质量密度ρ=7 800 kg/m3,铰接拱脚。每种模型计算了前7阶振型的自振周期,各模型周期计算结果见表3。

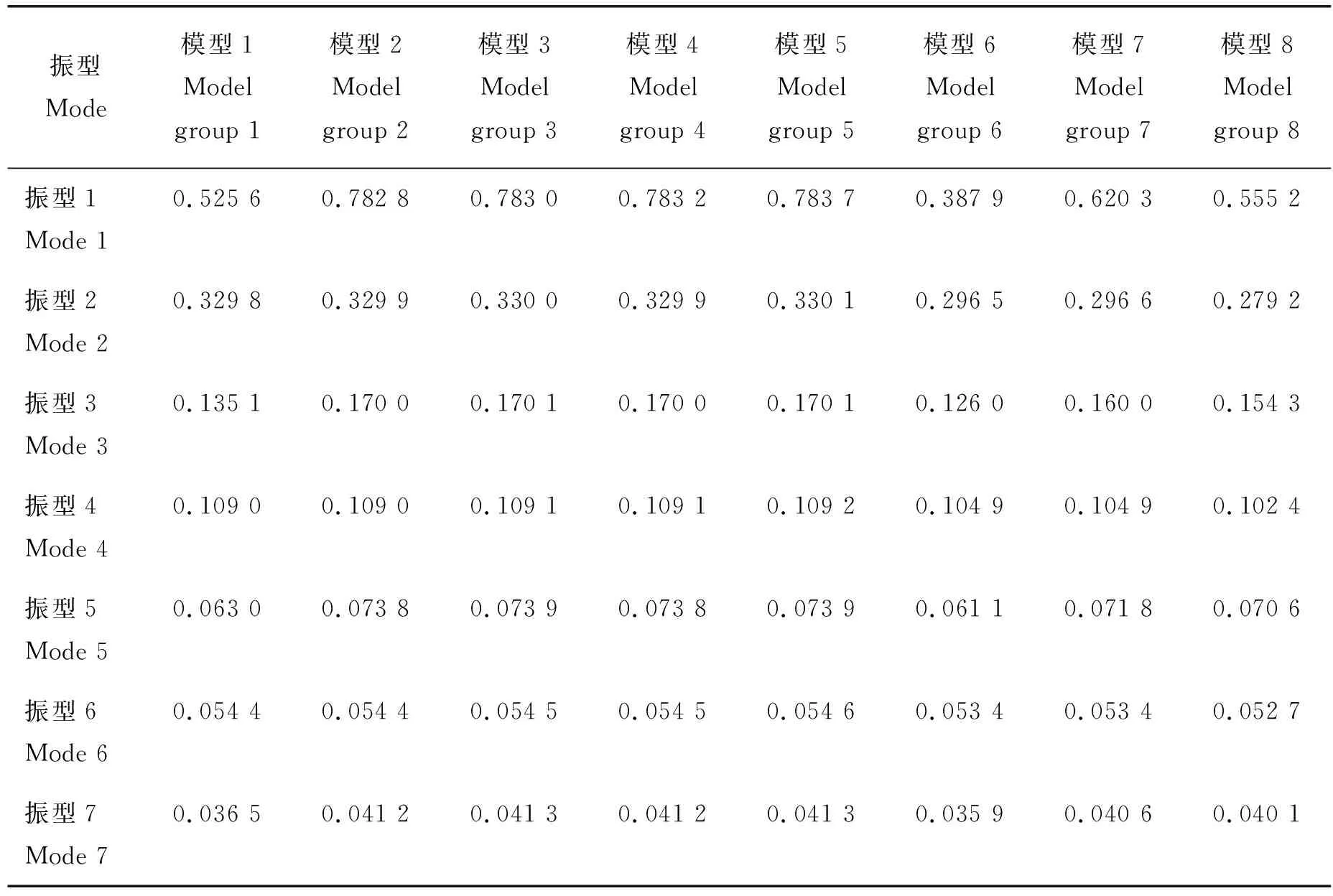
表3 拱棚不同模型自振周期计算结果Table 3 Calculation results of natural vibration period of different arch shed models s

3.2 典型拱形温室

选取拱跨度为10 m,失高2.5 m的典型拱形温室,计算2种不同结构型式下的自振周期:结构1,柱拱截面相同,均采用焊接薄壁圆钢管,截面规格为Φ51×2 mm;结构2,柱拱截面不同,柱子采用方钢管,截面规格为50 mm×50 mm×2 mm,拱采用圆钢管,截面规格为Φ40×2 mm。2种结构所用材料力学性质相同,弹性模量E=2.06×105MPa,剪切模量G=8.0×104MPa,剪应力不均匀系数μ=1.2,质量密度ρ=7 800 kg/m3。每种模型计算了前7阶振型的自振周期,各模型周期计算结果见表4。

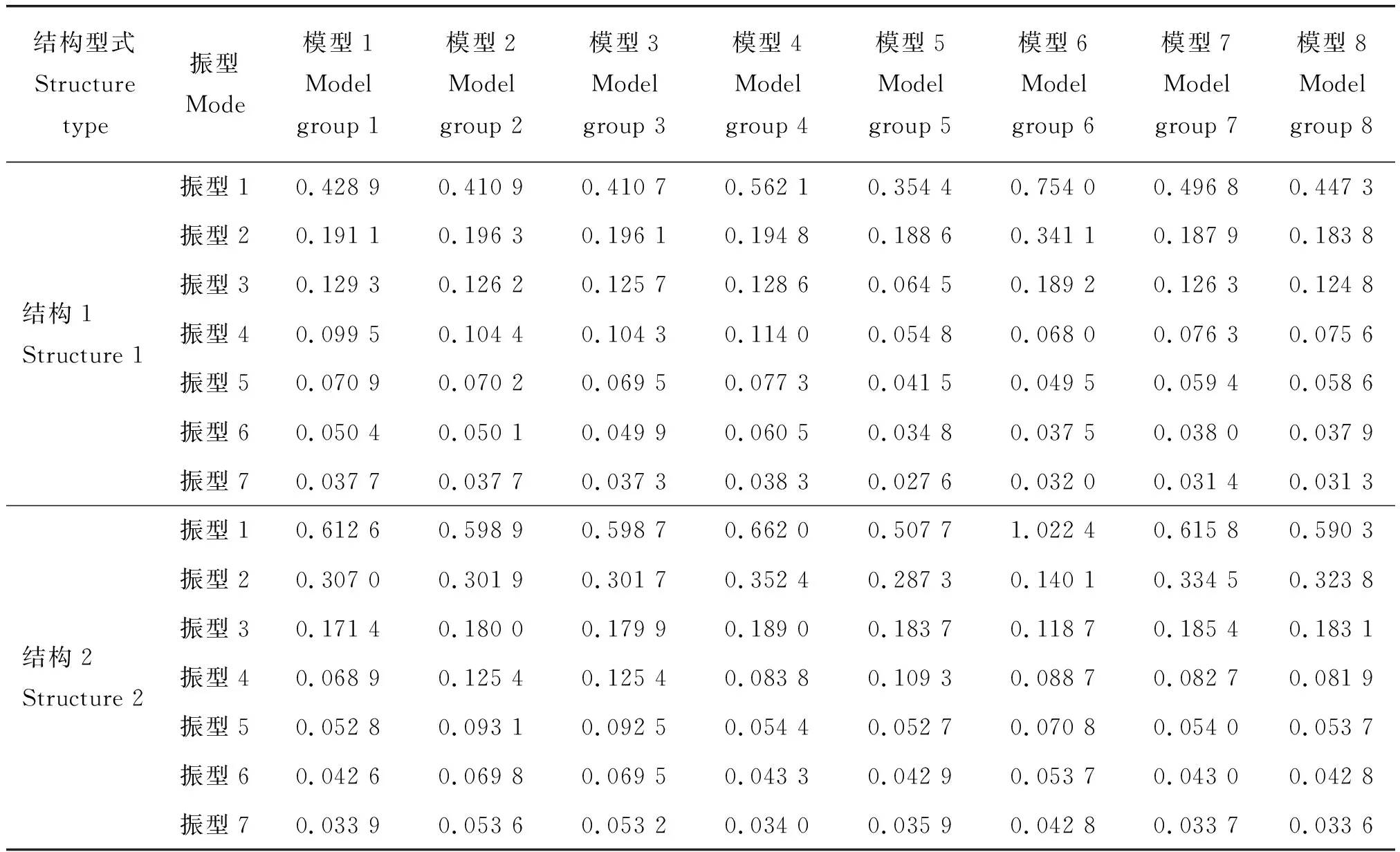
表4 典型拱形温室不同模型自振周期计算结果Table 4 Calculation results of natural vibration period of different models of typical arch greenhouse s

3.3 结果对比与分析

拱棚同一振型下每种模型与模型1的相对误差的计算结果见表5。可以看出:采用不同分析模型,得到的自振周期不同,基本规律是,平转动模型与平动模型的误差>40%;几何线性模型与几何非线性模型的误差>20%;Timoshenko梁模型与Euler梁模型的误差<0.1%;可压缩模型与不可压缩模型的误差<0.1%。产生这些差异的原因是,考虑的变形越多,结构刚度越小,自振周期越长。相比而言,转动惯量和二阶效应影响更为显著,工程计算中,为了得到计算简单、精度足够的拱形温室结构自振周期,应考虑平转动引起的结构变形和轴力产生的二阶效应,可忽略剪切变形和轴向压缩变形,故应考虑采用几何非线性可压缩平转动Euler梁模型。

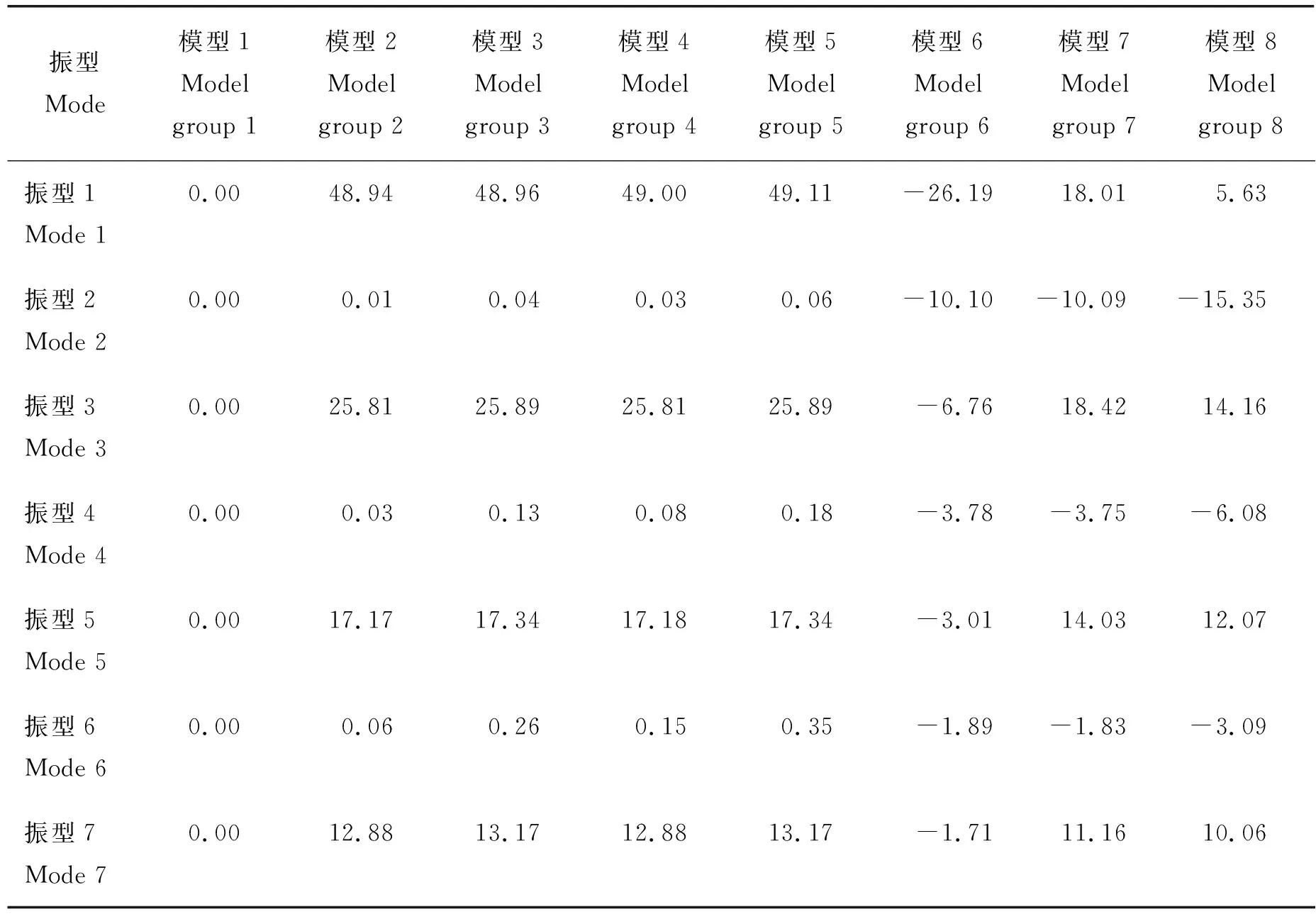
表5 拱棚各模型周期相对误差计算结果Table 5 Relative error calculation results of arch shed model period %

4 结束语

本研究在分析拱的弯曲变形、剪切变形、轴向压缩变形、二阶效应以及基于分布质量的平动惯性力和转动惯性力的基础上,建立了非线性平转动Timoshenko圆拱动力模型。根据不同的定解条件,提出了拱形温室结构的自振分析方法,实现了不同拱形温室结构的自振分析。采用本研究模型计算了拱棚和典型拱形温室结构在不同模型下的自振周期,对不同模型的计算结果进行分析表明,对于拱形温室结构,应考虑平转动和几何非线性引起的变形,可忽略剪切变形和轴向变形,故可采用几何非线性可压缩平转动Euler梁模型来计算其自振周期。