基于连续介质力学的泡沫混凝土应力-变形理论分析

孙 浩,杨 浩,王洪泽,宿 廷,秦立达

(1.内蒙古工业大学 理学院,内蒙古 呼和浩特 010051;2.塔塔电力勘测设计有限公司,内蒙古 呼和浩特 010011;3.内蒙古自治区住房和城乡建设厅,内蒙古 呼和浩特 010060)

连续介质力学作为力学学科重要的理论基础之一,普遍适用的研究对象为物质四态,即固体、液体、气体和等离子体[1-3]。连续介质力学主要研究的内容是外荷载作用下物体内的物质如何反应,即确定作为对外力的响应而引起的物体内部的情况。连续介质力学应用的学科领域包括材料科学、土木工程、航空航天等多个领域[4-6]。目前国内应用连续介质力学做学科基础应用研究的优秀研究团队及其团队所进行的研究工作主要有:清华大学水利水电工程系张建红教授研究团队在环境岩土工程领域应用连续介质力学研究滑坡从破坏启动、演化发展至最终沉积的运动规律[7-9];哈尔滨工业大学复合材料与结构研究所王友善教授研究团队结合连续介质力学研究橡胶表面失稳临界条件和失稳形貌演化规律[10-12];中国科学技术大学安徽省先进功能高分子薄膜工程实验室主任李良彬教授研究团队在连续介质理论的框架下运用数值模拟的研究手段揭示脆性材料和软材料中的高速断裂不稳定和极限裂纹速度的起源[13-15]。

泡沫混凝土是在胶凝材料、水和外加剂组成的复合料浆中引入泡沫并经浇筑及养护而成的轻质混凝土建筑材料[16-18]。泡沫混凝土具有质轻、良好的保温性能、优异的防火性和优越的抗震抗爆性等优势[19-21],因此其被广泛应用房屋建筑工程[22]、桥梁路面工程[23]、港口水利工程[24]和军事等领域[25-26]。目前泡沫混凝土材料的宏观性能已被研究学者广泛研究并且研究方法集中于试验研究,针对泡沫混凝土材料的力学理论分析研究较少,尤其是应用连续介质力学理论研究分析泡沫混凝土应力-变形鲜有报道。本文以泡沫混凝土作为研究对象,应用连续介质力学理论理论分析研究其应力状态和变形协调条件,为泡沫混凝土的研究应用提供力学理论指导。

1 张量

1.1 求和约定

求和约定指的是一个指标在某项内重复代表该指标在某个特定的范围内遍历求和。将遍历求和的指标称为哑指标;没有求和的指标称为自由指标。哑指标意味着求和,对于采用符号的形式并无实际使用要求。

在三维欧几里德空间中,笛卡儿坐标系x,y,z下具有分量dx,dy,dz的线元。线元长度的平方见式(1)。引入符号克罗内克δij将改写为式(2)的形式。表达式(2)成立的条件是:指标i和j的范围为1～3。

ds2=(dx)2+(dy)2+(dz)2

(1)

ds2=δijdxidxj

(2)

引入置换符号εrst,置换符号εrst和克罗内克δ对于张量表达来说非常重要,两者之间存在以下关系表达式(3),称为ε-δ恒等式。将求和约定推广至全微分表达,令f(x1,x2,…,xn)是一个有n个自变量x1,x2,…,xn的函数。其全微分表达式见式(4)。

εijkεist=δjsδklδ-δksδjt

(3)

(4)

1.2 笛卡儿张量解析定义

笛卡儿张量的解释定义是基于在一个笛卡儿直角坐标系转换到另一个笛卡儿直角坐标系过程中产生的,它具有特定的规则表达,矢量场或一阶张量场特定规则表达见式(5),x1、x2、x3表示变换前坐标,x1、x2、x3表示变换后坐标;二阶张量场特定规则表达见式(6)。

(5)

(6)

1.3 商法则

首先,考虑一组n3个函数,其简写形式为A(i,j,k),每个指标的范围都是1～n,其次考虑其是否是张量,为避免进行直接鉴定交换律的过程,需要假设A(i,j,k)与任意张量乘积的性质。最后,假设一个矢量ξi(x),乘积形式A(i,j,k)ξi(x)(对i采用求和约定)产生一个Ajk(x)型的张量,表达式见式(7),这样就能证明A(i,j,k)是一个Aijk(x)型的张量。上述的商法则性质不只局限于低阶张量,推广到更高阶的张量仍然适用。

A(i,j,k)ξi(x)=Ajk

(7)

1.4 偏导数

在仅考虑笛卡儿坐标时,任何张量场的偏导数都具有类似笛卡儿张量分量的性质。考虑两组笛卡儿坐标(x1,x2,x3)和(x1,x2,x3),其中ξi(x1,x2,x3)是一个张量,求偏导数后有式(8)的恒等表达式。在仅限于笛卡儿坐标时,倘若Φ,ξ和σij都是张量,则Φ,i,ξi,j,σij,k分别是一阶、二阶和三阶张量,常用逗号表示偏导数。

(8)

2 应力分析

2.1 应力的表示方法

考虑在泡沫混凝土中取直角平行六面体作为连续介质,以笛卡儿坐标系为参考系,坐标轴平行于泡沫混凝土平行六面体单元的各个棱边,具体如图1所示。垂直于x1的面的应力分量有τ11,τ12,τ13;垂直于x1的面的应力分量有τ21,τ22,τ23;垂直于x1的面的应力分量有τ31,τ32,τ33。正应力的应力分量有:τ11,τ22,τ33;其他分量τ12,τ13等称为剪应力。

图1 泡沫混凝土平行六面体单元应力分量标记

泡沫混凝土的应力是位于面元正侧(外法线正方向的一测)的部分对位于面元负测的部分的单位面积上的作用力。规定若泡沫混凝土平行六面体单元面元的外法线方向与坐标轴的正向一致,则对应的应力分量为正,具体应力分量的正方向如图2所示。

图2 泡沫混凝土平行六面体单元应力分量的正方向

2.2 运动方程和柯西公式

2.2.1 运动方程

牛顿运动定律是连续介质力学的基础,根据线动量的变化率等于作用在物体上的总外力联立方程可以得到表达式(9),称为运动方程。

(9)

2.2.2 柯西公式

从运动方程出发,可以导出的结论:表示面元外部材料对内部材料作用的应力矢量T(+)与表示内部材料通过同一面元对外部材料作用的应力矢量T(-)大小相等、方向相反。为证明泡沫混凝土的应力状态只由τij一组量来进行表征即可,柯西公式应用而生,具体表达式见公式(10) ,柯西公式所表达的物理意义是确定作用于物体中任意面元上的应力矢量的充分必要条件是应力τij有九个应力分量,τij称为应力张量。

(10)

2.3 平衡方程与边界条件

2.3.1 平衡方程

为了推导泡沫混凝土的平衡方程,在其内部取一个各面平行于坐标平面的微六面体,考察其静平衡状态,在不同表面上作用的应力如图3所示。泡沫混凝土微六面体作用的体力是Xidx1dx2dx3,作用的面力是左侧τ11dx2dx3和右侧[τ11+(∂x11/∂x1)dx1]dx2dx3等。

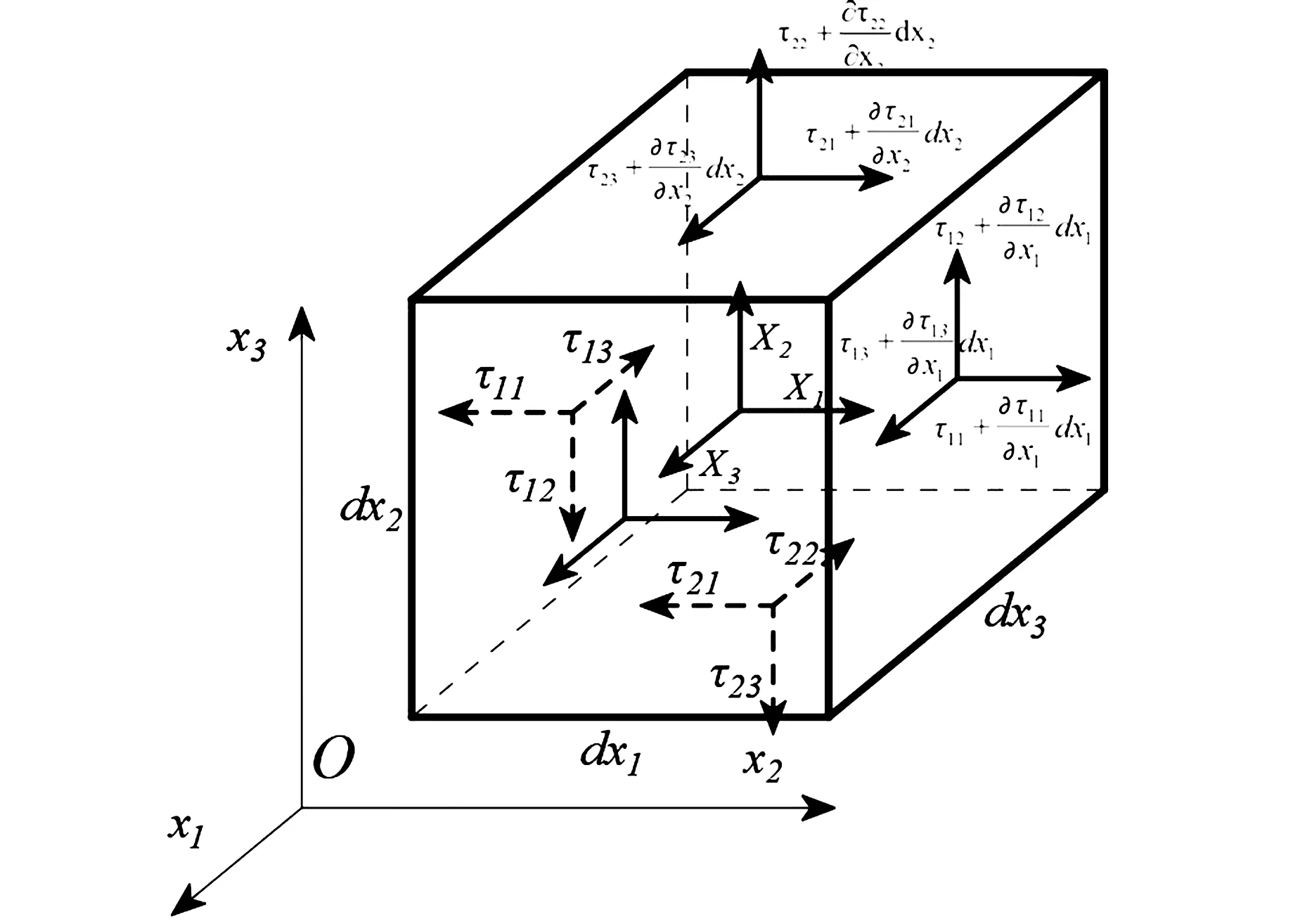
图3 泡沫混凝土平行六面体单元应力分量的平衡

(11)

平衡方程的表达式是在满足应力连续性假设基础上进行推导的,涉及的应力场是非均匀的,每个应力分量都是位置函数,根据物体平衡合力为零的条件,得到泡沫混凝土平衡方程的表达式见式(11)。微元的平衡还要求合力矩为零,通过对微元力矩列平衡方程后发现应力张量是对称的,即τij=τji。

2.3.2 边界条件

边界条件所表达的是与外部世界相关的已知事实,根据边界条件运用微分方程(场方程)求解物体内部的应力。如果能够找到所有满足泡沫混凝土平衡方程和边界条件的解,就可以清楚地描述其物体内部的完整信息。

2.4 平面应力状态

当考虑泡沫混凝土在xy平面内处于平面应力状态的情况时,其应力分量σzz,σzy和σzx在表表面上均为零,即满足式(12)。当泡沫混凝土由x-y至x′-y′坐标转动时,利用式(13)求解新坐标系下的应力分量,泡沫混凝土在平面应力状态下的坐标变化如图4所示。利用坐标变化,假设x′和y′为主轴,给出特殊θ值相应的x′和y′轴的方向称为主方向,得到泡沫混凝土坐标变化后的σx′、σy′和τx′y′,具体的表达式见式(13)和式(14)。

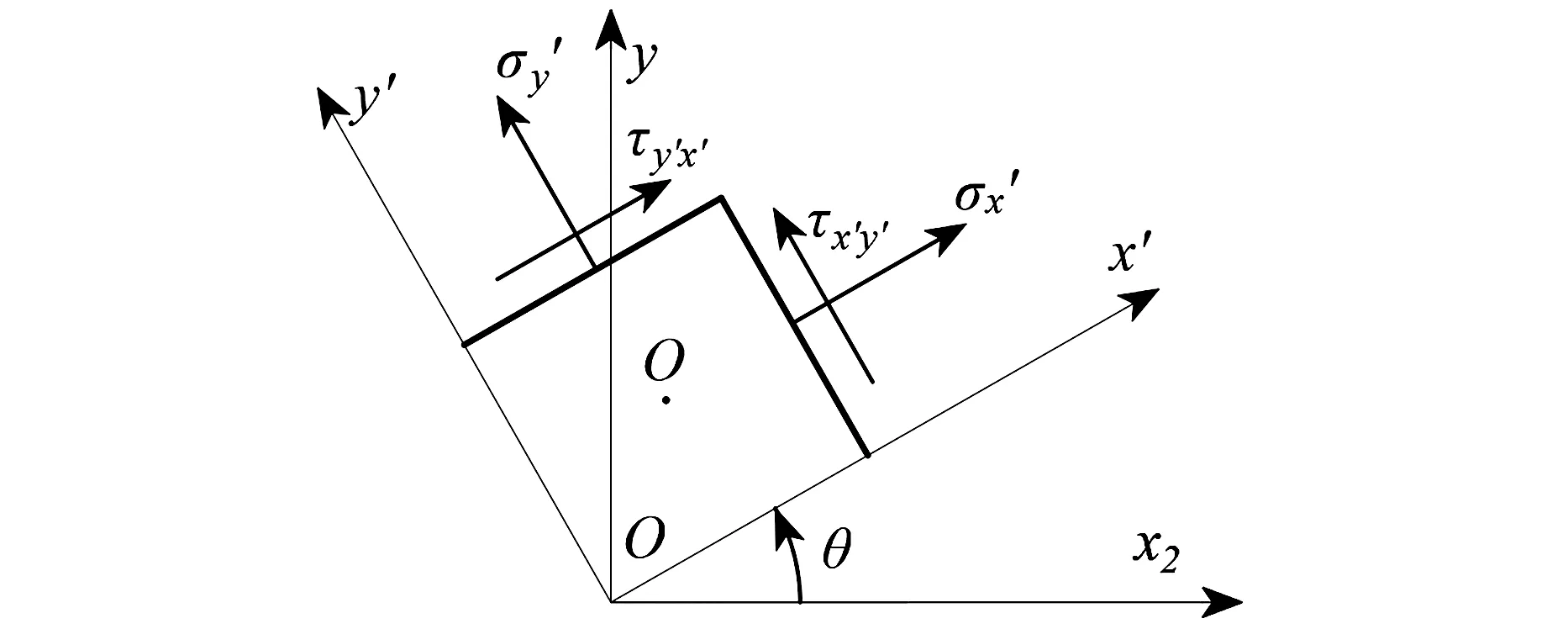
图4 泡沫混凝土平面应力状态的坐标变化

σzz=σzy=σzx=0

(12)

(13)

(14)

2.5 主应力与剪应力

2.5.1 主应力

当泡沫混凝土材料处于一般应力状态时,在法线为ν的平面上,作用的应力矢量与v的方向有关。在物体内的给定点处,应力矢量与法线ν夹角与平面的方向有关,随之发生变化。在物体内部任意一点至少有三个相互正交的平面满足应力矢量与该平面相互垂直。满足上述条件的平面称为主平面,其法线为主轴,作用在主平面上的正应力称为主应力。由式(15)求解系数行列式为零得到关于σ的三次方程式(16),根与系数之间的关系见式(17)。

(τji-σδji)νj=0 (i=1,2,3)

(15)

(σ-σ1)(σ-σ2)(σ-σ3)

(16)

I1=σ1+σ2+σ3

I2=σ1σ2+σ2σ3+σ3σ1

I3=σ1σ2σ3

(17)

2.5.2 剪应力

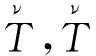
(18)

3 变形分析

3.1 变形

采用与泡沫混凝土应力状态相关的方法分析其变形。泡沫混凝土在承受微小的单轴拉伸应变时,在一定范围内满足式(19)的关系,即胡克定律。泡沫混凝土承受微小剪应变的方程关系见式(20),两个关系式中,E和G均为常数,分别是弹性模量和剪切模量。

σ=Eε

(19)

τ=Gtanα

(20)

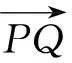
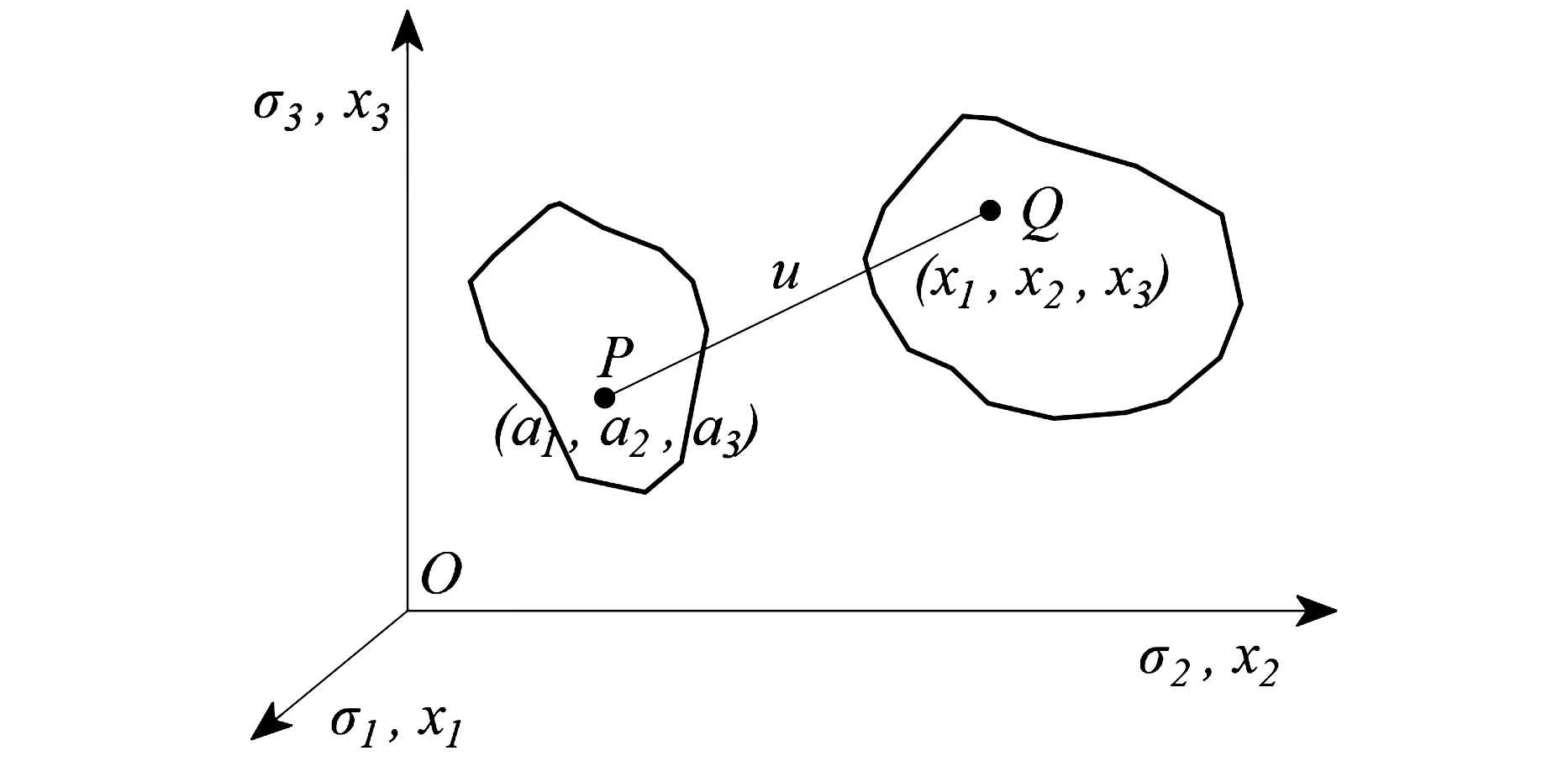
图5 泡沫混凝土位移矢量

3.2 应变

分析物体变形的关键是对于物体内任意两点间的长度变化进行描述,位移本身并不直接与应力相关。图6表示泡沫混凝土内部相邻三点的变形,点P(a1,a2,a3)和相邻点P′(a1+da1,a2+da2,a3+da3)的连接为无限小线元,初始线元PP′长度的平方见式(21),变形后的新线元QQ′长度的平方见式(22),得到两线元的平方差见式(23)和式(24),Eij称为格林应变张量,eij针对小应变情况时应用,称为阿尔曼西应变张量。

图6 泡沫混凝土内部相邻三点的变形

(21)

(22)

(23)

(24)

3.3 用位移表示应变分量

当引入位移矢量u时,经过推导与简化后柯西小应变张量的表达式见式(25)。格林应变张量和阿尔曼西应变张量在泡沫混凝土内部一点位移无限小情况时区别就消失了,因此对于变形前或变形后的点位求位移导数是不重要的。

(25)

3.4 小应变分量的几何解释

设x,y,z作为一组笛卡儿直角坐标系。研究对象为平行于x轴(dy=dz=0)、长度为dx的线元。由变形引起的该线元长度平方的变化见式(26),略去二阶小量得到式(27),可以看到exx表示平行于x轴矢量的单位长度的长度变化,图7表示上述讨论中体积微元的应用。在工程应用中,应变分量eij的两倍,即2eij,被称为剪切变形。

图7 体积微元的应用

(26)

(27)

3.5 变形协调条件

对于得到的含有两个未知函数的偏微分方程来讲,想要得到精确解需要满足可积性条件,即协调方程。泡沫混凝土处于平面应变状态时,其协调方程见式(28),张量表达式为式(29)。当变形为小应变情况时,得到的协调方程表达式见式(30),它表示的81个方程中,有6个是基本方程。当变形是有限情况时,协调方程通过黎曼定理变形后的物体依然保持欧几里德空间这一依据推导得到。

(28)

(29)

eij,kl+ekl,ij-eik,jl-ejl,ik=0

(30)

4 结论

(2)泡沫混凝土在xy平面内处于平面应力状态的情况时,其应力分量σzz,σzy和σzx在表面上均为零。

(3)泡沫混凝土在承受微小的单轴拉伸应变时,在一定范围内满足胡克定律;其变形可以用位移场进行描述。