一类四阶Neumann边值问题解的存在性

黄永峰

(昌吉学院数学系,新疆昌吉 831100)

由上式知,

0 引 言

近年来,高阶边值问题因其在物理及工程学中较高的应用价值而受到广泛的关注.一些学者研究了高阶边值问题正解的存在性,得到了一些较好的结果[1,2].在研究中,学者们利用锥拉伸或锥压缩定理以及不动点指数理论在非线性项满足超线性或次线性条件获得结论.此外,还有学者利用临界点理论及Morse理论研究了高阶边值问题解的存在性[3-6].特别地,文献[4]利用临界点理论和Morse理论并结合局部环绕定理得到了四阶带参数Dirichlet边值问题解的存在性,文献[6]运用鞍点定理及临界点理论得到了四阶带参数的Neumann边值问题的解的存在性.基于以上的研究工作,本文考虑如下的问题,

1 预备知识

令 E=C[0,1]为[0,1]上的连续函数并按范数 ‖u‖C=tm∈[a0x,1]|u(t)|构成的实Banach空间, L2[0,1]为[0,1]上所有平方可积的函数构成的实Hilbert空间,其范数为,

设 Gi(t,s)为线性边值问题,

由此知,边值问题在 C4[0,1]中的解等价于下列方程,

在 C[0,1]中的解.

易知,G(t,s)为连续的,且边值问题的解等价于积分方程,

令,

在 C[0,1]中的解.

定义算子 K,

则边值问题在C4[0,1]中的解当且仅当其为算子方程,u=Kf→u,在 C[0,1]中的解.

为了证明需要,下面给出一些临界点理论及局部环绕的基本定义和引理.

定义1[7]设D是实Banach空间E中的开集,泛函J:D→R1在D上是Frechet可微,若有,u0∈D,使得J′(u0)=0,则称,u0是泛函J的一个临界点.

定义2[7]设 E实Banach空间,J∈C1(E, R1).如果,{un}⊂ E,J(un)→c,J′(un)→θ,n→∞,蕴涵{un}有收敛子列,则称泛函J满足(PS)c条件.如果对于所有的c均满足(PS)c条件,则称泛函J满足PS条件.

定义3[8]设J(θ)=0,E=V⊕X,dimV＜+∞,X为实Banach空间.如果存在ρ＞0,使得,

那么称J在θ点局部环绕.

定义4[8]设 u0是泛函J的一个孤立临界点, J(u0)=c,U是u0的一个邻域,且在U中,J除u0外没有其他临界点,称,

Cq(J,u0)=Hq(Jc∩U,(Jc∩U){u0}),q=0,1,2,…,为J在u0的第 q个临界群,其中,Hq(X,Y)为第 q个奇异相对同调群,其系数为整数群.若至少有一个临界群是非平凡的,则称 u0是J的一个同调非平凡临界点.

引理1[9]算子方程,u=Kf→u,在 C[0,1]中有解,当且仅当,v=K1/2f→K1/2v,在L2[0,1]中有解.

引理2[3]如果泛函,

有一个临界点,u∈L2[0,1],则边值问题在 C4[0, 1]中有一个解.

引理3[8]假设J∈C1(E,R1)满足 PS条件,且在θ点局部环绕,则θ为J的一个同调非平凡临界点.

2 主要结论及证明

引理4[6]假设(H1)及(H2)满足,那么存在M∞＞0使得,

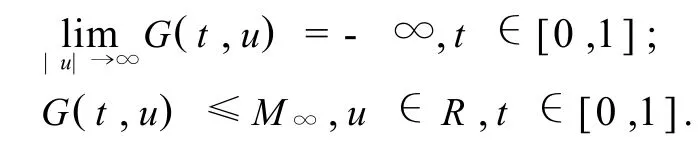
取{un}∈L2[0,1],使得 ‖un‖→∞,且有J(un)≤C,其中,C ∈R为常数.定义 vn= un/‖un‖,取其子列不妨仍记为{vn},使得存在 v0∈L2[0,1],有{vn}弱收敛到 v0,且 ‖v0‖≤1.同时,由 K1/2的全连续性知,K1/2vn→K1/2v0于 L2[0, 1],同时有,

引理5 假设(H1)及(H2)满足,那么有:

(i)J在L2[0,1]是强制的,即 J(u)→+ ∞,‖u‖→∞;

(ii)J满足PS条件.

证明 (i)假设(H1)及(H2)满足,令,

则由引理4知,

由上式知,

故,(Kv0,v0)=λ0‖v0‖2.v0=±ρ0e0,ρ ∈(0,1],K1/2v0(t)≠0,t∈[0,1],并有,

因此,当 n→∞时,

由上式的矛盾知假设不成立.因此,J在L2[0, 1]是强制的.

定理1 假设 f(t,0)=0,对(H1)、(H2)和(H3)满足,那么边值问题至少有2个平凡解.

证毕.

3 应用举例

考虑边值问题,

其中,

通过计算知,

[1]Liu B.Positive Solutions of Fourth-oder Boundary Value Problems[J].Appl Math Comput,2004,148(1):407-420.

[2]Pang C,Dong W,Wei Z.Multiple Solutions for Fourth-order Boundary Value Problem[J].J Math Anal Appl,2006,314(1): 464-476.

[3]Liu X,Li W.Existence and Multiplicity of Solutions for Fourth Order Boundary Value Problems with Parameters[J].J Math Anal Appl,2007,327(1):362-375.

[4]Yang Y,Zhang J.Existence of Solutions for Some Fourth-order Boundary Value Problems with Parameters[J].Nonlinear Anal, 2008,69(1):1364-1375.

[5]Han G,Xu Z.Multiple Solutions of Some Nonlinear Fourth-order Beam Equations[J].Nonlinear Anal,2008,68(1):3646-3656.

[6]黄永峰.一类带参数的四阶Neumann边值问题解的存在性[J].昌吉学院学报,2011,26(1):104-108.

[7]郭大钧.非线性泛函分析[M].济南:山东科学技术出版社,2001.

[8]Chang K.Infinite Dimensional Morse Theory and Multiple Solution Problems[M].Boston:Birkhauser Press,1993.

[9]Li F,Liang Z,Zhang Q.Existence of Solutions of a Class of Nonliear Second Order Two-point Boundary Value Problems[J].J Math Anal Appl,2005,312(1):357-373.

[10]LiuJ.The Morse Index of a Saddle Point[J].Systems Sci Math Sci,1989(2):32-39.

[11]ZhangJ,Li S.Muitiple Nontrivial Solutions for Some Fourth Order Semlinear Elliptic Problems[J].Nonlinear Anal,2005,60 (1):221-230.