Bernstein算子矩阵法求高阶弱奇异积分微分方程数值解

单锐，魏金侠，张雁

（燕山大学理学院，河北秦皇岛066004）

Bernstein算子矩阵法求高阶弱奇异积分微分方程数值解

单锐，魏金侠，张雁

（燕山大学理学院，河北秦皇岛066004）

为了求高阶变系数且带有弱奇异积分核Volterra－Fredholm积分微分方程的数值解，提出了Bernstein算子矩阵法.利用Bernstein多项式的定义及其性质给出任意阶弱奇异积分的近似求积公式，同时也给出Bernstein多项式的微分算子矩阵.通过化简所求方程及离散化简后的方程，可将原问题转换为求代数方程组的解.最后，通过收敛性分析说明该方法是收敛的，并用数值算例验证了方法的有效性.

高阶变系数；弱奇异；积分微分方程；Bernstein多项式；算子矩阵；数值解

Bernstein多项式在数学的各个领域有着重要的应用，这些多项式经常被用来求解积分方程、微分方程的数值解以及近似理论分析［1］.近些年来，越来越多的积分、微分方程的数值解通过各种多项式的算子矩阵求得.文献［2］利用Bernstein多项式的算子矩阵求解微分方程；Maleknejad等［3］利用Bernstein多项式的算子矩阵求解非线性Volterra－Fredholm－Hammerstein积分方程.积分微分方程数值解问题一直是研究的重要课题.许多科学与工程领域的问题都可以转化为积分微分方程［4－5］.其中，Volterra－Fredholm积分微分方程是一类人们特别感兴趣的方程，已经给出了很多种数值算法.文献［6］使用Legendre小波求解Fredholm积分方程；文献［7］利用Cattani′s方法求一类线性Fredholm积分微分方程；文献［8］采用Bernstein算子矩阵法求解高阶线性Volterra－Fredholm积分微分方程组.然而，对于高阶变系数并含任意阶弱奇异积分核的Volterra－Fredholm积分微分方程的数值解的研究较少.本文通过Bernstein多项式及其算子矩阵对这类方程进行讨论，将求原方程的数值解问题转化为求解代数方程组，使得计算大大简化.

1 Bernstein多项式及其性质

1.1 Bernstein多项式［8］

结合Bernstein多项式及其算子矩阵，考虑如下形式积分微分方程，有

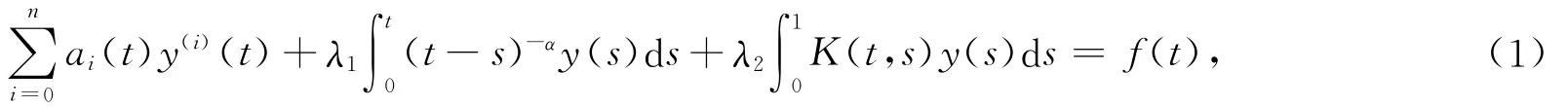
满足的初始条件为y（n－1）（0）＝yn－1，y（n－2）（0）＝yn－2，…，y（0）＝y0.式中：K（t，s），f（t），ai（t）为已知的连续函数；y（t）为未知函数且y（t）∈L2（［0，1］）；y（i）（t）为y（t）的i阶导数；λ1，λ2，α为常数，且0＜α＜1.

定义1 n次Bernstein多项式定义为

2 任意阶弱奇异积分的近似求积公式

设y（s）∈L2（［0，1］），考虑如下弱奇异积分

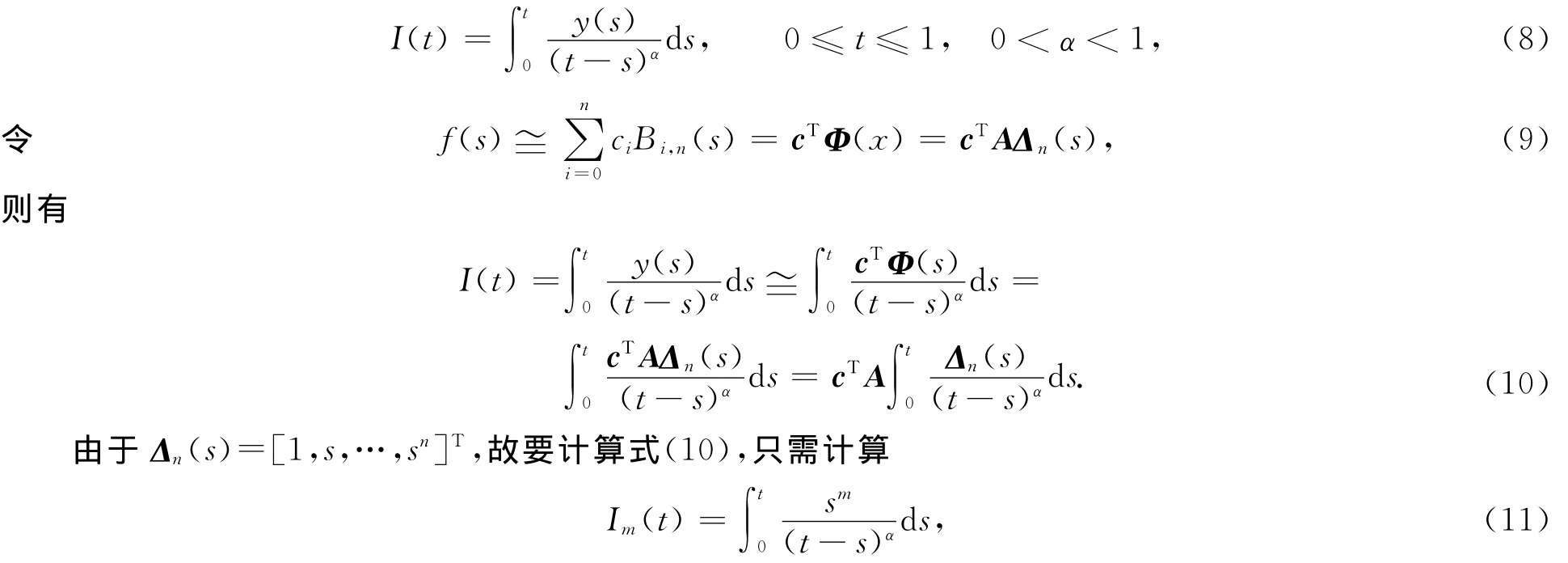
式（16）即为弱奇异积分的近似求积公式.

3 Bernstein多项式的微分算子矩阵［8］

设Φ′（x）＝FΦ（x），其中F是（n＋1）×（n＋1）阶矩阵，称为Bernstein多项式微分算子矩阵.由式（4）可知

此时，可以得到Bernstein多项式微分算子矩阵为

如果y（x）≅cTΦ（x），则对于i≥2，有

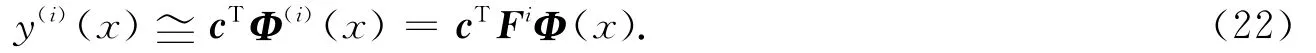
4 Bernstein算子矩阵法求解高阶积分微分方程

5 收敛性分析

引理1［9］设ym（i）（t）＝cTFiΦ（t）为y（i）（t），i＝1，2，…，n的近似解，则对于任意ε＞0，存在正整数Ni，i＝1，2，…，n，使得当m＞Ni时，对∀t∈［0，1］，有‖ym（i）（t）－y（i）（t）‖＜ε.其中：c＝［c0，c1，…，cn］T；Φ（x）＝［B0，m（x），B1，m（x），…，Bm，m（x）］T

引理2［9］设ym（t）＝cTΦ（t）为y（t）的近似解，则对于任意ε＞0，存在正整数Nn＋1，使得当m＞Nn＋1时，对∀t∈［0，1］有‖ym（t）－y（t）‖＜ε.其中：c＝［c0，c1，…，cm］T；Φ（x）＝［B0，m（x），B1，m（x），…，Bm，m（x）］T.令

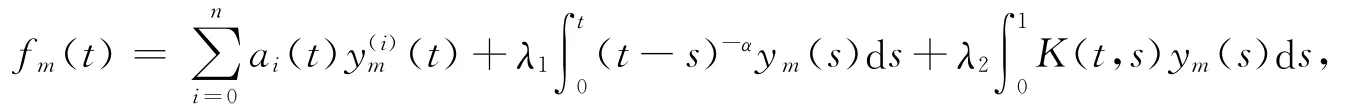
则有如下定理.

定理1 若y（i）m（t），ym（t）的定义同上，对任意ε＞0，存在正整数N，使得当m＞N时，有‖fm（t）－f（t）‖＜ε.

证明 由于ai（t），i＝0，1，2，…，n为［0，1］上的连续函数，故存在正整数Mi，i＝0，1，2，…，n，使得∀t∈［0，1］，有‖ai（t）‖≤Mi.

6 数值算例

考虑Volterra－Fredholm积分微分方程

4（t＋s）y（s）d s＝f（t）.（31）式（31）中：f（t）＝65t4＋32t3＋7

∑i＝0

tiy（i）（t）＋∫t

0

（t－s）－1／2y（s）d s＋∫1

0），其精确解为y（t）＝t4＋2t3.取n分别为n＝4，n＝5，n＝6，用MATLAB软件计算数值解与精确解的绝对误差，如表1所示.

10t＋1730＋

Γ（11／2）＋2πt9／2Γ（5）πt7／2Γ（4）Γ（9／2

表1 数值解与精确解的绝对误差Tab.1 Absolute error of numerical solution and exact solution

计算结果表明，结合Bernstein多项式的算子矩阵，上述方法可以对含高阶变系数且带有弱奇异积分核Volterra－Fredholm积分微分方程进行数值求解，验证了该方法的有效性和可行性.同时通过表1，可以看到所提方法具有高精度，且使用较强.

7 结论

利用Bernstein多项式并结合算子矩阵的思想，对变系数做了有效的离散.将变系数且带有弱奇异积分核Volterra－Fredholm积分微分方程转化为熟悉的线性代数方程，从而更容易计算机求解.通过收敛性分析，理论上说明了所提方法是收敛的.数值算例进一步表明，该方法所得数值解精度高，且计算量小，是一种有效的算法.

参考文献：

［1］ MALEKNEJAD K.A new approach to the numerical solution of Volterra integral equations by using bernstein′s approximation［J］.Commun Nonlinear Sci Numer Simul，2011，16（2）：647－655.

［2］ YOUSEFI S A，BEHROOZIFAR M.Operational matrices of bernstein polynomials and their applications［J］.Internat J Systems Sci，2010，41（6）：709－716.

［3］ MALEKNEJAD K，HASHEMIZADEH E，BASIRAT B.Computational method based on bernstein operational matrices for nonlinear Volterra－Fredholm－hammerstein integral equations［J］.Commun Nonlinear Sci Numer Simul，2011，17（1）：52－61.

［4］ DELVES L M，MOHAMED J L.Computational methods for integral equations［M］.Cambridge：Cambridge University Press，1985.

［5］ SCHIAVANE P，CONSTANDA C，MIODUCHOWSKI A.Integral methods in science and engineering［M］.Boston：Birkhäuser Boston，2002.

［6］ RAZZAGHI M.The legendre wavelets operational matrix of integration［J］.Int J Syst Sci，2001，32（4）：495－502.

［7］ MALEKNEJA K.An efficient numerical approximation for the linear class of Fredholm integro－differential equations based on Cattani′s method［J］.Commun Nonlinear Sci Numer Simulat，2011，16（7）：2672－2679.

［8］ MALEKNEJAD K.A Bernstein operational matrix approach for solving a system of high order linear Volterra－Fredholm integro－differential equations［J］.Mathematical and Computer Modelling，2012，55（3／4）：1363－1372.

［9］ PHILLIPS G M.Interpolation and approximation by polynomials［M］.New York：Springerr，2003.

Bernstein Operational Matrix Method for Solving the Numerical Solution of High Order Integro－Differential Equation with Weakly Singular

SHAN Rui，WEI Jinxia，ZHANG Yan
（College of Sciences，Yanshan University，Qinhuangdao 066004，China）

In order to obtain the numerical solution for high order variable coefficients Volterra－Fredholm integro－differential equation with weakly singular kernels，we present a Bernstein operational matrix method in this paper.A approximate formula which solves solution for any arbitrary order weakly singular integral is given by using the definition of Bernstein polynomial and some properties，and a operational matrix of derivative of Bernstein polynomial is also obtained.By translating the original problem through simplifying and descreting the equation，the problem can be transferred into a system of algebraic equations.Convergence analysis shows that the method is convergent.The numerical example shows that the method is effective.

high order variable coefficients；weakly singular；integro－differential equation；Bernstein polynomial；operational matrix；numerical solution

O 241.8

A

（责任编辑：陈志贤 英文审校：黄心中）

1000－5013（2012）05－0595－06

2012－03－01

单锐（1961－），女，教授，主要从事偏微分方程、积分微分方程数值解和最优化理论的研究.E－mail：weijinxiaymx201366＠163.com.

河北省教育厅科学研究计划项目（2009159）