可以不失表达力而又避免说谎者悖论吗?
赵 震
(北京大学哲学系,北京100871)
1.引言
悖论有语形悖论、语义悖论、语用悖论等几种。语形悖论的典型代表是罗素悖论,其产生的根源在于“一方面,二阶逻辑的概括公理要求满足任意可表达条件的一些对象都可以形成概念,也就是说概念是对象的幂集;另一方面,公理V又要求概念不同当且仅当概念的外延不同,也就是说概念和外延(对象)之间是一一对应的……然而根据康托定理,这两个方面的要求不能同时得到满足”(刘靖贤,2011)。语用悖论的代表是考试悖论。说谎者悖论是语义悖论的典型代表。说谎者悖论是这样一类句子,说它真则它非真,说它非真则它真。按照我们的常识,悖论句子的存在意味着这个推理系统微不足道,一个微不足道的系统可以推出任何东西来,而这就使得这个系统变得没有意义了,一个什么都能推出来的系统和一个什么都推不出来的系统是一样的。在所有的解悖方案中,塔尔斯基的解悖方案最经典,但是,塔尔斯基的方案有一些问题,比如,塔尔斯基自己提出的(T)模式被打碎成了不同的(Tn)模式,可是常识是语言中只有一个T而不是一系列的Tn,这也是这个方案最被诟病的地方。本文试图给出一种解悖方案,它可以在只有一个(T)模式的情况下避免说谎者悖论而又不失表达力。
2.我的方案
首先,我将构造一个逻辑LCQ。
2.1 LCQ 的语形
给定极限序数 γ=ω。语言L0包括谓词符号:;常项符号①这里的上标0表示语言建构的层次。后面会说到T谓词只能应用于句子的名称,而那些不是句子名称的常项在被用到T谓词时所构成的句子都是假的,初始的常项不是句子的名称,所以它们的下标是⊥,根据后面的语义这样的句子永假。,…和e1,e2,e3,…。L0中没有函数符号,所有的n元函数符号都按照通常的做法被处理为n+1元谓词符号。此外,句法中没有通常的量词符号∀和∃,取而代之的是很多∀α以及相应的∃α,α<γ,以及另外两个特殊量词

接下来我们定义LT中的公式和句子。既然LT中没有函数符号,那么其中的项就只有常项和变项。
(2)Formun+1:如果φ是Formun中的公式,那么它是Formun+1中的公式;Tdi是公式,di是Ln+1中项;…di是公式,d1…di是Ln+1中的项;如果φ是公式是公式;如果φ和ψ是公式是公式;如果φ是公式,∀αφ是公式,其中;如果φ是公式,是公式按照通常的方式被定义。
(3)Formu=∪{Formuα:α<γ}。
句子是Formu中没有自由变项的公式。
2.2 LCQ的语义学
下面给出语言LT的语义学:对于任意LT模型,论域AT-是非空集合;IT-是谓词和第二类常项的解释;VT-是指派,为每一个变项和第一类常项指派AT-中一个个体。(1)对于任意常项ei,IT-(e)i是AT-中的一个元素;(2)对于常项是AT-中的元素;(3)对于变项xi,VT-(x)i是AT-中的元素;(4)对于谓词符号是(AT)-i的子集((AT)-i是i个AT-的卡氏积),在LCQ中谓词T被当做一个普通谓词来处理IT(-T)是AT-的子集;(5)对于公式,这里的di项;(6)对于公式对于公式或者对于公式对于任意,这里的Mα=max:任给对于公式对于LT中任意常项(c)),相应的,对于公式.存在LT中常项
2.3 LCQ的公理化
公理:
推理规则:
2.4 LCQ的可靠性
LCQ的可靠性可以按照通常的方式直接证明。
2.5 LCQ的完全性
LCQ的完全性证明和一阶逻辑的完全性证明很相似,唯一的区别是见证集的定义和与量化公式有关的步骤。
定义1.设Γ是一致的句子的集合。如果有一个常项的集合D,使得任给LT∪D中的至多只包含一个自由变项的公式ψ(x)和φ(x),如果∃αxψ(x)∈Γ,那么存在常项d∈D,使得⊆Γ,并且如果,那么存在常项d∈D使得成立,那么我们说D包含LT的见证。D被称作Γ的见证集。
定理1. 设W是一个一致的LT理论,D是新常项的集合,使得D∩LT=φ,L′=LT∪D并且|D|=|LT|。存在一个一致的L′的句子的集合W′使得W⊆W′并且D是W′的见证集。
证明:假设 λ=|D|=|LT|并且 D={dξ:ξ<λ}。令{ψξ:ξ<λ}是LT∪D 中至多只包含一个自由变项的公式的集合。定义一系列集合 Wξ,ξ<λ,如下:
(1)W0=W。
(3)对于极限序数 ξ,Wξ=∪β<ξWβ。
显然,W0⊆W1⊆…令 W′=∪ξ<λWξ,下面归纳证明 W′是一致的:
(1)W0=W,根据假设W0是一致的。
(2)假设Wξ是一致的。如果是不一致的并且也是不一致的,那么Wξ+1=Wξ,因此Wξ+1是一致的。如果是一致的并且Wξ∪{xχ}是不一致的,那么我们可以证明是LT中公式且β>α}是一致的。首先我们证明Wξ∪是LT中公式且β>α}是一致的。假设并非如此,即是LT中公式 β>α}是不一致的,则一定有LT中公式χ和λ>α,使得并且又因为dη是新常项,所以一定有。既然,可以得出,又根据公理(10),Wξ∪{∃αxψξ(x)}是不一致的。这与假设矛盾。所以是一致的。根据公理(8)是成立的,所以也是成立的。进而是成立的。因此是LT中公式且β>α}是一致的。假设Wξ∪{xχ}是一致的并且是不一致,既然dζ是新常项是一致的。如果是一致的,那么根据上面的定义和证明中公式且是一致的。
(3)对于极限序数λ,如果Wλ是不一致的,那么存在α<λ,使得Wα是不一致的。但是,根据归纳假设,任给α<λ,Wα是一致的。所以Wλ是一致的。
定理2. 假设W是一致的LT理论,D是一个新常项的集合。那么W有一个模型U,使得U中每一个元素是D∪C中一个常项的解释,即A={aU:a∈D∪C},这里的C是LT中的常项的集合且U⊨W。
证明:根据Lindenbaum定理,W可以被扩张为一个极大一致的LT语句的集合W′。那么存在一个语言L′T使得L′T=LT∪D,D∩LT=Ø 并且|D|=|LT|。根据定理 1,W′可以扩充为一个L′T的句子的一致集 W″,使得D是其见证集。然后根据Lindenbaum定理,我们可以把W″扩充为L′T的一个极大一致的句子集W*,使得D是其见证集。
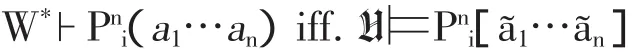
接下来将证明任给LT∪D 公式以及

定理3. 完全性定理:假设Σ是LT是公式的集合,ψ是LT的公式。如果Σ⊨ψ,那么Σ├ψ。特别地,如果⊨ψ,那么├ψ。等价地,如果Σ是一致的那么Σ是可满足的。
证明:假设Σ⊨ψ,但是Σ├/ψ,那么显然Σ∪{ψ}是一致的。令E是新常项的集合,使得|E|=|LT|并且。把中的公式排列成一个线性序。按下面的方式用E中的新常项代替中的自由变项:任给公式φ,用E中之前的代替之后得到的公式中未出现过的常项来做代替,并且用相同的常项代替相同的变项,不同的常项代替不同的变项;对于Σ中的句子,保留其原形式。令是按照上述方法代替中公式得到的句子的集合。因此W∪{ψ′}是E∪LT的句子的集合。令D是任意新常项的集合,使得,并且根据定理可以扩充为一个以D为见证集的一致的集合 W′;根据定理 2,W′有一个模型 U′,令 U 是,那么存在模型B,使得任给中任意公式的变项xi,令,这里的ei是中的对应公式里用来代替 xi的常项。对于其他常项t和谓词Q,令。显然,任给公式中的公式因此存在模型B,使得,并且,即,并且。但是,这与矛盾。所以如果Σ⊨ψ,那么 Σ├ψ。
2.6 LCQ与一阶逻辑(FOL)的对应
首先,定义一个从FOL的公式到LCQ的公式的翻译函数ft如下:(1)对于原子公式,其中di是常项或变项;(2)对于公式对于公式对于公式,相应地,对于公式
下面证明从FOL到LCQ的对应:
命题1.任给一阶公式φ和模型σ,σ⊨φiff.σ⊨ft(φ)
证明:(1)如果φ是原子公式,显然σ⊨φiff.σ⊨ft(φ);(2)布尔代数情况显然;(3)如果φ=∃xχ并且σ⊨∃xχ,那么存在一个d∈M,使得σ(x/d)⊨χ,根据归纳假设,σ(x/d)⊨ft(χ),因此,或者存在常项c使得 σ(c)=d,因而 σ⊨xχ,所以;或者不存在常项c,得 σ(c)=d,因而d∈M1,因此,进而。如果φ=∃xχ并且,那么或者σ⊨∃1xft(φ)因此存在d∈M1使得σ(x/d)⊨ft(χ),根据归纳假设σ(x/d)⊨χ,既然M1⊆M,d∈M,因此σ;或者,那么存在一个常项c,使得,根据归纳假设又因为 σ(c)∈M,因此 σ⊨∃xχ。
2.7 基于LCQ的真理论TCQT
2.7.1TCQT的公理
TCQT公理是LCQ公理加上下面这条(T)模式公理:
2.7.2TCQT的一致性
定理4. 存在模型τ,使得TCQT在τ中是可满足的。
证明:
令σT=<D,I,V>是一个代数模型,使得定义域D由所有自然数组成。定义模型σT如下:
首先,为L0中的每一个第一类常项解释为自然数,使得任给n,I(c0⊥n)=n,谓词P21解释为后继关系,P31解释为加法关系,P32解释为乘法关系,为每一个逻辑常项、第二类常项、变项和其他谓词指派一个哥德尔编码。然后为每一个L0中公式φ指派一个哥德尔编码。这些L0中公式的指派构成D的一个子集D0。然后为L1—L0(表示L1中属于L1但不属于L0的部分)中每一个新常项、谓词T以及每一个新公式指派一个D—D0中的编码。由此,每一个Ln中的常项、变项、谓词和公式都被指派到D—Dn-1中的一个编码。
根据上面的赋值,对于任意常项cαφΔ和cβχΔ,如果α≠β或者φ≠χ,那么σT(cαφΔ)≠σT(cβχΔ);其他谓词的解释任意,σT(T)={σT(cα+1φ1):σT(‖φ‖)=1},其中α是φ中上标最大的序数。
接下来证明(T)模式在这个模型中是成立的:
下面将证明任给公式(开公式或闭公式)φ,σT⊨φ iff.σT⊨Tcα+1φΔ。
首先证明从右到左的方向:假设σT⊨T(cα+1φΔ),那么σT(cα+1φΔ)∈σT(T),由σT(T)的定义,σT(‖φ‖)=1。如果 φ=Pijd1…di,并且Pij≠T,那么根据透明算子的定义,‖Pijd1…di‖=Pijd1…di,因此 σT⊨φ;如果 φ=Tdi,并且存在一个常项cαχΔ,使得di=cαχΔ,那么σT(‖Tdi‖)=σT(‖χ‖)=1,进而σT(cαχΔ)∈σT(T),又因为di=cαχΔ,所以σT(di)∈σT(T),因此σT⊨Tdi;如果φ=Tdi,并且不存在常项cαχΔ,使得di=cαχΔ,那么‖Tdi‖=Tdi,因此 σ(TTd)i=1,即 σT⊨Tdi;如果φ=ψ,并且 σ(T‖ψ‖)=1,那么 σ(T‖ψ‖)=1,进而并非 σ(Tcα+1ψΔ)∈σ(TT),根据归纳假设并非 σT⊨ψ,因此 σT⊨ψ;如果φ=ψ∨χ,既然 σ(Tcα+1φ∨χΔ)∈σ(TT),那么 σ(T||ψ∨χ||)=1,根据透明算子定义,σT(‖ψ∨χ‖)=σT(‖ψ‖∨‖χ‖)=1,进而σT(‖ψ‖)=1或者σT(‖χ‖)=1。因此σT(cα+1ψΔ)∈σT(T)或者σT(cα+1χΔ)∈σT(T),进而σT⊨Tcα+1ψΔ或者σT⊨Tcα+1χΔ,根据归纳假设σT⊨ψ或者σT⊨χ,所以σT⊨ψ∨χ;如果φ=⊗xψ,既然σT(cα+1⊗xψΔ)∈σT(T),那么σT(‖⊗xψ‖)=1,根据透明算子的定义,σT(⊗x‖ψ‖)=1,进而任给d∈K(或者存在d∈K),σT(x/d)(‖ψ‖)=1,这里的K=Mα+1或者K=V,进而σT(x/d)(cα+1ψΔ)∈σT(x/d)(T),所以σT(x/d)⊨Tcα+1ψΔ,根据归纳假设σT(x/d)⊨ψ,所以σT⊨⊗xψ。
接着证明从左到右的方向:假设σT⊨φ,如果φ=Pijd1…di,并且Pij≠T,那么根据透明算子的定义,‖Pijd1…di‖=Pijd1…di,所以σT⊨‖Pijd1…di‖,即σT(‖Pijd1…di‖)=1,根据T的解释,σT(cα+1φΔ)∈σT(T),这里的α是Pijd1…di中上标最大的序数。因此σT⊨Tcα+1φΔ;如果φ=Tdi,那么σT⊨Tdi,进而σT(di)∈σT(T),进而存在常项cαψΔ,使得σT(di)=σT(cαψΔ),并且σT(‖ψ‖)=1,根据透明算子的定义,σT(‖Tdi‖)=σT(‖ψ‖)=1,因而σ(Tcα+1T(d)iΔ)∈σ(TT),这里的 α 是Tdi中出现的上标中的最大序数。所以 σT⊨T(cα+1T(di)Δ);如果φ=ψ,那么σT⊨ψiff.σT⊨/ψ,所以并非 σT⊨ψ。根据归纳假设,并非 σT⊨T(cα+1ψΔ),即 σ(Tcα+1ψΔ)∉σ(TT),这里的 α 是ψ中出现的最大的序数,因而 σ(T‖ψ‖)≠1。进而 σT( ‖ψ‖)=1,因此 σT(‖ ψ‖)=1。所以 σ(Tcα+1ψΔ)∈σ(TT)。因此 σT⊨T(cα+1ψΔ);如果φ=ψ∨χ,那么 σT⊨ψ∨χiff.σT⊨ψ或者 σT⊨χ。根据归纳假设,σT⊨T(cδ+1ψΔ)或者σT⊨T(cγ+1χΔ),这里δ和γ分别是ψ和χ中出现的上标的最大序数,所以σT(cδ+1ψΔ)∈σT(T)或者σT(cγ+1χΔ)∈σT(T)。因此σT(‖ψ‖)=1或σT(‖χ‖)=1。进而σT(‖ψ‖∨‖χ‖)=1,即σT(‖ψ∨χ‖)=1,根据σT(T)的解释,σT(cα+1ψ∨χΔ)∈σT(T),这里的α是{δ,γ}的最大值。因此σT⊨T(cα+1ψ∨χΔ);如果φ=⊗xψ,那么σT⊨⊗xψiff.任给d∈K(或者存在d∈K),使得σT(x/d)⊨ψ。根据归纳假设,σT(x/d)⊨T(cα+1ψΔ),这里的α是ψ中出现的上标的最大序数,进而σT(x/d)(‖ψ‖)=1,所以σT(⊗x‖ψ‖)=1,进而σT(‖⊗xψ‖)=1,所以σT(cα+1⊗xψΔ)∈σT(T)。所以σT⊨T(cα+1⊗xψΔ)。
3.如何避免新版本的塔尔斯基定理
塔尔斯基定理:令(L,N)是任意被解释的形式语言,它包括否定和哥德尔编码g(x),使得任给L-公式A(x)存在一个公式B,使得B↔A(g(x))成立。令T*是N中为真的L-句子的哥德尔编码的集合。那么不存在L-公式True(n)来定义T*。也就是说不存在L-公式True(n),使得任给一个L-公式A,都有True(g(A))↔A成立。
这个定理的目的是说,不存在语言中可定义的谓词能够满足(T)模式,不论这个理论是什么,除非这个理论是不一致的。但是,为什么使用哥德尔编码来表达T模式中句子的名字呢?我们可以使用其他的常项作为名字。这不仅仅是名字的变化,而且可以避免塔尔斯基定理。当然仅仅使用新符号并不能避免塔尔斯基定理,因为我们可以设定这些符号和哥德尔编码之间的一个一一对应,然后建构一个与这些新符号有关的新版本的塔尔斯基定理。所以,这里所说的“避免”塔尔斯基定理意味着我们可以保留(T)模式而不会构造出一个新版本的塔尔斯基定理。避免新版本的塔尔斯基定理的方式是防止新版本的对角线定理。下面说明如何避免新版本的对角线定理。
首先表明通常的对角线定理的建构。对角线定理的证明的关键是哥德尔句的构造,首先我们需要一个带一个自由变项的开公式:

这里的P(χ)是任意以x为唯一自由变项的开公式,self-application表示用上面这个开公式的名字(哥德尔编码)替代v的所有自由出现。令D(v)表示上面的这个开公式,并且<D(v)>是这个开公式的名字。令S是D(v)的自应用之后得到的下面这个句子:

但是S的名字<S>是<D(v)>的唯一的self-application。然后我们可以得到:

进而可以得到:

如果我们把谓词P(x)变为T(),那么和塔尔斯基(T)模式一起,可以得到 T(<S>)↔T(<S>)。矛盾。
但是,这个建构在我们的方案中并不成立。因为我们的量词是∃α和 而不是∃,所以相应的公式应表达为:
∃1x(xis the self-application of<D(v)>∧P(x))∨x(xis the self-application of<D(v)>∧P(x))为了使用(T)模式,我们需要常项cαφ0,而不是<φ>,这里的φ就是上述公式,由此可以得到

4.总结
首先,有两种命名方式:编码和特殊常项。通过编码我们可以建构自指的句子和对角线定理,但是(T)模式并不能应用于编码名字。因此,避免了说谎者悖论。(T)模式可以应用于特殊常项,但是根据语言的建构和推理规则,自指和对角线定理不成立,因此也避免了说谎者悖论。与此同时,塔尔斯基的(T)模式的本质被保留了,即“任给句子φ,φ是真的 iff.Φ”。另外,这个方案并不弱,PA可以在其中被表达。
[1]刘靖贤.游走于可数无穷[J].哲学门,2012,13(1).
[2]C.C.Chang,H.J.Keisler.Model Theory[M].New York:Elsevier Publishing Company,INC,1990.
[3]R.T.Cook.Counterintuitive consequences of the revision theory of Truth[J].Analysis,2002,62(1).
[4]H.Field.Saving Truth from Paradox[M].New York:Oxford University Press,2008.
[5]H.Friedman,M.Sheard.An axiomatic approach to self-referential truth[J].Annals of Pure and Applied Logic,1987,(33).
[6]A.Gupta,N.Belnap.The Revision Theory of Truth[M].Cambridge,Massachusetts:The MIT Press,1993.
[7]V.Halbach.Tarskian and Kripkean logic[J].Journal of Philosophical Logic,1993,26(1).
[8]J.Ketland.Yablo’s paradox and ω-inconsistency[J].Synthese,2005,145(3).
[9]S.Kripke.Outline of a theory of Truth[J].The Journal of Philosophy,1975,72(19).
[10]A.Tarski.The semantic concept and the foundations of semantics[J].Philosophy and Phenomenological Research,1944,4(3).
[11]S.Yablo.Paradox without self-reference[J].Analysis,1993,53.
[12]刘靖贤.良莠不齐反驳[J].湖南科技大学学报:社会科学版,2011,14(6).
——论胡好对逻辑谓词的误读

