双参数算子半群Yosida 的逼近性质

仓定帮， 陈 藏， 闫守峰

(1.华北科技学院 基础部，北京101601;2.华北科技学院 教务处，北京101601)

20 世纪中期，为了解决偏微分方程的初值问题，以E.Hille 与K.Yosida 为代表的一些数学家提出了Banach 空间上强连续半群理论［1-2］。现今，强连续半群的理论已经成为许多领域(除了传统的偏微分方程和随机过程外，还包括量子力学、无穷维控制理论、积分-微分方程、泛函微分方程及无穷维动力系统等)的重要工具。近年来，双参数算子半群由于与下面的双参数抽象柯西问题(ACP)的密切关系重新得到了很多学者的重视与研究［3-6］。

其中，Hi:D(Hi)⊆X →X i = 1，2 为线性算子。

文中对双参数算子半群展开进一步探讨，给出了Banach 空间上双参数算子半群生成元的Yosida逼近定义，得到了双参数算子半群可微性与一致算子拓扑下的连续性的充要条件，对单参数算子半群的相关研究方法加以推广。

1 定义与引理

定义1［4］设L 为Banach 空间，T(s，t)，s ≥0，t ≥0，为L 中的有界线性算子，∀s1，s2，t1，t2≥0，T(s，t)称为双参数半群。如果满足:

1)T(0，0)= I，I 为单位算子;

2)T(s1+ t1，s2+ t2)= T(s1，t1)T(s2，t2)，

若存在常数ω，M ＞0，使得‖T(s，t)‖≤Meω(s+t)成立，则称双参数半群是指数有界的。

引理1［4］双参数算子半群T(s，t)的无穷小生成元是变换R+2→B(L)，由下面的表达式定义:

其中，A1，A2定义如下:

并且

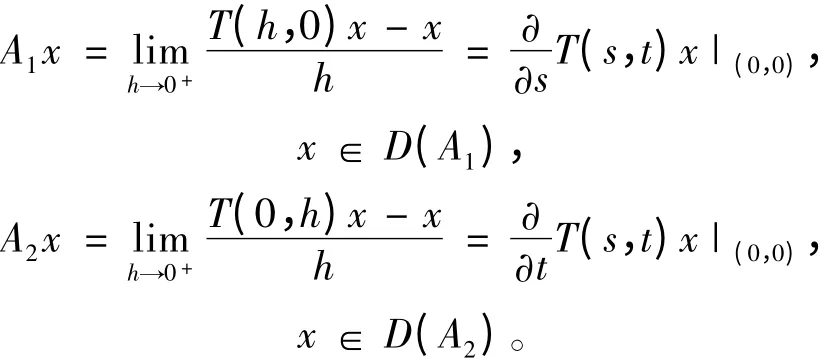
同时还有

及

引理2［4］设T(s，t)为Banach 空间L 中的双参数算子半群，无穷小生成元为(A1，A2)，若

且

则有

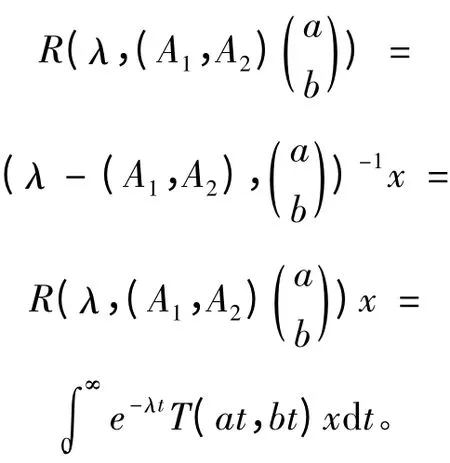
显然，可以发现若T(s，t)是指数有界的，则有

定义2 设T(s，t)为Banach 空间L 中的双参数算子半群，无穷小生成元为(A1，A2)，定义

称Lλ为Yosida 逼近。

2 主要结论

定理1 设T(s，t)为Banach 空间L 中的双参数算子半群，则

其Yosida 逼近满足下列结论:

证 当λ →+ ∞时，

再根据Yosida 逼近的定义可知:

定理2 设T(s，t)为Banach 空间L 中的双参数算子半常数群，无穷小生成元为(A1，A2)，A1，A2均为稠定闭算子，Lλ为Yosida 逼近，若T(s，t)是强连续的，则T(s，t)在点(s，t)s≥s0，t≥t0可微的充要条件是存在常数M ＞0，使得对

成立。

证 先证明必要性。假设T(s，t)在点(s，t)s≥s0，t≥t0是可微的，则

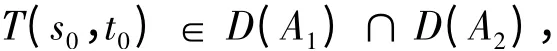
由定理1 可得

从而存在常数Mx＞0，使得

成立。再根据共鸣定理可知，

成立。

下证充分性。假设(A1，A2)为双参数算子半群T(s，t)的生成元，并且存在常数M ＞0，使得对

成立。再据定理1 可知

又因为A1，A2是稠密算子，可以证明上面的极限对任意得到x ∈X 成立。又因为

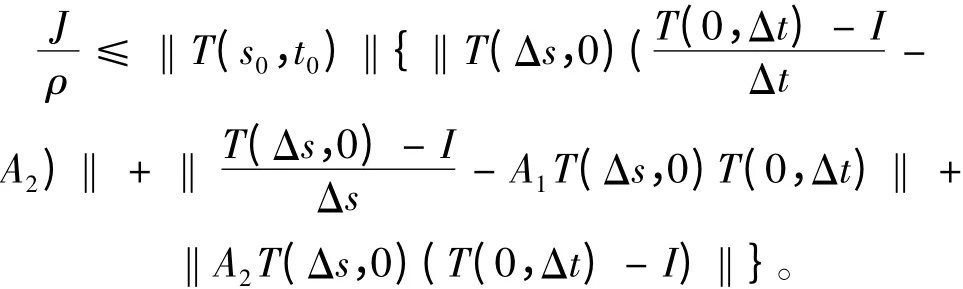
根据双参数半群的连续性及其指数有界性，可以看出

即T(s，t)在点(s，t)s≥s0，t≥t0是可微的。

推论1 设T(s，t)为Banach 空间L 中的双参数算子半常数群，无穷小生成元为(A1，A2)，A1，A2均为稠定闭算子，Lλ为Yosida 逼近，若T(s，t)是强连续的，且对

成立，则T(s，t)在点(s，t)可微，并且

定理3 设T(s，t)为Banach 空间L 中的指数有界的双参数算子半常数群，无穷小生成元为(A1，A2)，A1，A2均为稠定闭算子，Lλ为Yosida 逼近，则T(s，t)一致算子拓扑连续的充要条件为

证 先证明必要性。因为双参数半群指数有界，即‖T(s，t)‖≤Meω(s+t)，所以由引理1 可得

从而当λ ＞max{ω(A1)，ω(A2)}时，对δ ＞0，有

因此

又由δ ＞0 的任意性和T(s，t)一致算子拓扑连续性可知

成立。

则对∀ε ＞0，存在常数λ0＞0 使得下面不等式

成立。

令0 ＜Δt ＜ε，0 ＜Δs ＜ε，因为

其中

又有

所以T(s，t)是一致算子拓扑连续的。

［1］Hille E.Representation of one-parameter semigroups of linear transformations［J］.Nat Acad Sci，1942，28:175-178.

［2］Yosida K.On the differentiability and representation of one-parameter semigroups of linear operators［J］.J Math Soc Japan，1948，1:15-21.

［3］Arora S，Sharda S.On two parameter semigroup of operator［D］.New Delhi:University of Delhi，1990:147-153.

［4］Sharif S A，Khallr.On the generator of two parameter semigroups［J］.Applied Mathematics and Computation，2004，156(2):403-414.

［5］Janfada M.On two-parameter regularized semigroups and the Cauchy problem［J］.Bull Austral Math，2004，69:383-394.

［6］Khanehgir M，Janfada M，Niknam A.Two-parameter integrated semigroups and two-parameter abstract Cauchy problems［J］.Jour of Inst of Math and Comp Sci (Math)，2005，1(18):1-12.