单磁铁悬浮系统自激振动的稳定性分析及抑制
黎松奇, 张昆仑
(西南交通大学磁浮技术与磁浮列车教育部重点实验室,四川成都 610031)
EMS型磁悬浮列车作为一种新型的交通工具,在其理论研究和工程实践中,出现了一些特有的现象.在德国和日本的列车运行实验中均出现了车辆结构性振动的情况,即使车体静态悬浮,也可能与轨道以及桥梁产生自激振动[1].多年以来,各国专家一直在研究和探讨该问题[2].
文献[3]对磁浮车调试过程中出现的钢轨道框架和车辆共振现象进行了理论研究,指出磁浮车二次悬挂和钢框架的垂向频率相同会引起系统共振.文献[4]用Nyquist准则分析了简化车-轨系统的稳定性,提出了使用虚拟调谐质量阻尼器控制振动的方法.文献[5]采用谐波平衡法分析了磁悬浮系统非线性振动现象,证明了只要轨道存在弹性,车-轨耦合振动不可避免.文献[6]通过系统的开环传递函数和相频曲线分析了系统稳定的充分条件,为系统设计提出了基本的稳定性要求.文献[7]利用中心流形对各种耦合振动的情况进行了分岔方程的推导以及仿真分析.文献[8-9]通过数值仿真的方法对车体以及弹性桥梁在耦合振动过程中的动力学行为进行了分析.文献[10-11]研究了控制系统时滞对于磁浮车-轨非线性耦合振动的影响.文献[12]建立了通过全状态反馈控制的单磁铁悬浮系统,讨论了通过粒子群算法对控制器参数优化的具体方法.
在上述文献中没有在理论上对悬浮控制器参数以及车-轨系统参数在静态悬浮过程中对于稳定性的影响给出较好的解释.本文通过建立简化的单磁铁悬浮系统车体-悬浮架-轨道系统动力学模型,对磁浮列车静态悬浮自激振动稳定性问题进行了分析,讨论了系统参数对于稳定性的影响,给出了系统主要参数和稳定性之间关系的表达式,并讨论了运用瞬时最优控制抑制车-轨自激振动的具体方法.
1 车辆-轨道系统的数学模型
1.1 车辆动力学方程
本文主要分析起浮后车辆静态悬浮时发生的自激振动,所以只考虑车辆-悬浮架-轨道的垂向自由度,忽略二系悬挂和轨道形变以外的其他干扰.简化的单磁铁悬浮系统力学模型如图1所示.
图1中:
fe为电磁吸力;
m2、m3分别为悬浮架和车体的质量;
z1、z2分别为悬浮架和车体的实际位移;
h为轨道的位移;
c为悬浮架与轨道之间的距离;
x为车体横向位移;
k3为二系悬挂刚度;
c3为二系悬挂阻尼.
系统中参考方向取向下为正.

图1 单磁铁悬浮系统力学模型Fig.1 Mechanical model of single magnet suspension system
由图1所示模型可知 c=z1-h,同时,悬浮架和车体的动力学方程为

式中:
Fs为二系悬挂产生的力,

其中,F0为二系悬挂在平衡点的力.
电磁铁产生的吸力可表示为

式中:N为线圈匝数;
A为有效面积;
μ0为真空磁导率;
i为线圈电流.
在平衡点(i0,c0)处求偏导可得
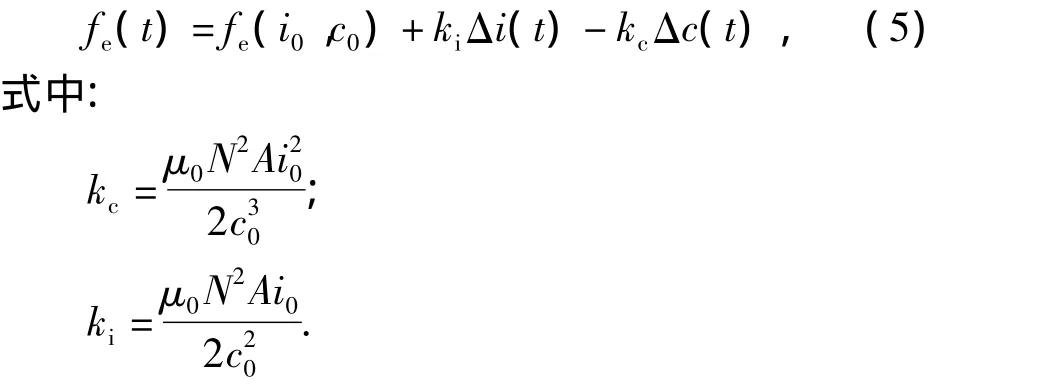
目前有多种方法控制电流对于电压的滞后[13],本文直接使用电流作为控制输入.采用工程中常用的PID算法,令:c为间隙,c'为间隙变化速度,z″1为悬浮架加速度为反馈变量,kp、kv、ka为控制器参数,c0为额定的悬浮气隙,控制电流表示为
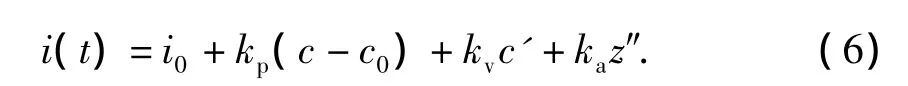
联立式(1)、(5)、(6),可求得平衡点处fe-c的关系.
令:k2为平衡点处的等效磁隙刚度;c2为平衡点处的等效磁隙阻尼.则fe(t)又可以表示为

1.2 轨道动力学方程
轨道模型采用在磁浮系统研究中广泛使用的Bernoulli-Euler(BE)梁方程

式中:
EI为抗弯刚度;
c为轨道阻尼;
ρA为轨道线密度;
F(x,t)为负载.
采用模态分解法处理后得轨道位移的微分方程为

式中:Mn为广义质量;
Φn(x)为轨道第n阶模态;
Qn(t)为第n阶的广义力;

εn为轨道的n阶阻尼比;
ωn0为轨道n阶固有频率;
L为轨道长度.
由式(11)可得

当单独考虑第n阶模态作用时,令:

则轨道位移方程可表示为

综上所述,当单独考虑第n阶模态作用时,系统的动力学方程可以表示为

2 振动稳定性分析
先考虑轨道一阶模态单独作用的情况,将式(13)移动到平衡点,令:

为状态变量,得到系统状态矩阵为


系统的特征方程为

式中:I为单位矩阵.
系统稳定的基本条件为 ai>0(i=0,1,2,…,6),则系统稳定必须能满足 b3>0,b4>0,b5>0,b6>0.代入b1~b6值,整理得到轨道一阶模态单独作用下系统稳定的条件为

同理,当轨道第n阶模态单独作用时,稳定条件为

当系统控制参数不变时,二系悬挂参数和轨道参数的基本关系为
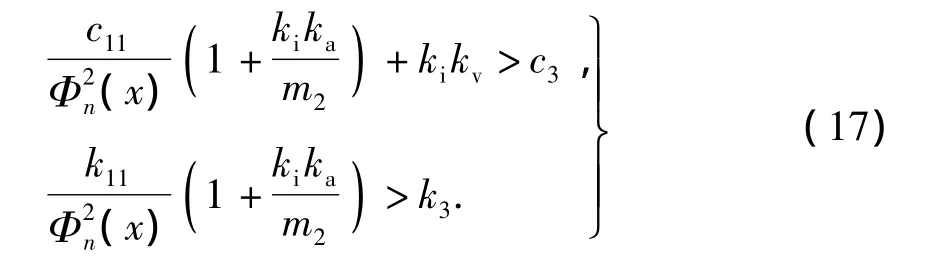

故轨道模态阶数越大,k1n和c1n值也越大,所以,当轨道一阶模态单独作用时能满足式(15),其他模态单独作用时也能满足式(16).
综上所述,在选用c、c'和z″1为控制器反馈变量时,系统稳定性条件如式(15)所描述.代人k1n和c1n解析式,分析可知:
(2)轨道的抗弯刚度EI越大,系统越稳定;轨道结构阻尼越大,系统越稳定;轨道长度L越小,系统越稳定,但为了提高稳定性而修改以上3个参数,都会显著增加线路的成本;
(3)车体质量m2越小,系统越稳定,该条件对车体的轻量化设计提出了要求;
(4)系统的控制器参数影响稳定性,被控制器参数决定的k2和c2过大或者过小都不利于系统稳定,同时考虑到系统需要产生能保持在平衡点的力,k2满足

(5)由式(15)、(16)可知,由于系统稳定性和系统成本相互矛盾,所以在一定的轨道和车辆参数条件下,系统可能产生剧烈的自激振动;在系统参数满足式(17)的情况下,通过调节控制参数可以使系统稳定性增加,使自激振动变小;如果系统控制参数无论如何调节,都无法满足式(17)时,只能通过修改系统物理参数的方法减小振动,如k1n非常小(当EI非常小,或者L非常大).
3 抑制振动的瞬时最优算法
从前面的分析可知,当系统满足式(17)时,稳定性可以通过控制器参数调节,此时系统可以通过调节k2或c2取值增加系统稳定性.从式(7)中参数可以看出,当系统固定时由于ki和kc是常量,所以k2取值需由控制参数kp和ka调节,c2取值可以通过kv和ka调节.且由于调节ka会改变系统惯性,其作用相当于改变了系统的质量,通常采用调节kp和kv的方法.
本文采用瞬时最优控制算法来确定控制器参数的具体取值.该方法与传统的最优控制算法相比,并不是求取整个过程中的全局最优指标,而是针对任意时刻取局部最优指标,能够避免求解在传统的最优控制中使用Riccati方程,在工程应用中能够实现快速的计算.
瞬时最优算法的描述如下.
系统运动方程描述为

式中:y(t)为位移向量;
M、C、K分别是系统质量矩阵、阻尼矩阵和刚度矩阵;
f(t)为外激励向量;
D为外激励向量的位置矩阵;
u(t)为主动控制力向量;
E为控制力位置矩阵.
可将式(18)改写为状态空间形式
x'(t)=A2x(t)+Bu(t)+Hf(t),
式中:

取性能指标[14]

式中:Q和R为权矩阵,分别代表结构和控制力的强调程度.
求解式(19)是约束条件下系统最优控制问题,可得瞬时最优控制力为

式中:
Δt为控制算法的时间间隔.
当单磁铁悬浮模块发生振动时,取z1、z'1、c 和c'为补偿反馈,可由式(20)直接求出抑制振动的瞬时最优补偿力u(t),代人式(7),根据一定的权重分解出需要的k2和c2,再通过k2、c2与控制器参数关系求解kp和kv的取值,最后根据补偿值修正控制器参数.悬浮控制系统工作的原理如图2所示.

图2 悬浮控制系统工作原理Fig.2 Working principle of the suspension control system
4 系统仿真
本文采用Matlab中的Simulink工具箱建模,进行车-轨振动数值仿真.采用某磁浮车-轨系统的主要参数如下:车体质量为2 000 kg,悬浮模块质量为750 kg,磁铁面积为0.024 m2,轨道线密度为6 900 kg/m,轨道阻尼比为 0.005,轨道长度为24.8 m,轨道抗弯刚度为 2.43 ×104MN·m2,额定悬浮间隙为0.008 m,二系悬挂刚度为50 kN/m,二系悬挂阻尼为10 kN/(m/s),悬浮架横向位置L/2.
为简化表达,令:

车体在t=0时刻开始起浮,记录系统20 s内的振动情况,ωc为控制器特征频率,ωs为二系悬挂固有频率.
(1)参数正常情况
当仿真中系统参数都取正常情况(仿真1),结果如图3(a)所示,车体迅速到达平衡状态,悬浮架与轨道振动随着时间减小.放大图形可以看出,车-架-轨振动的主要频率来自于二系悬挂.
计算系统稳定条件(式(15)):
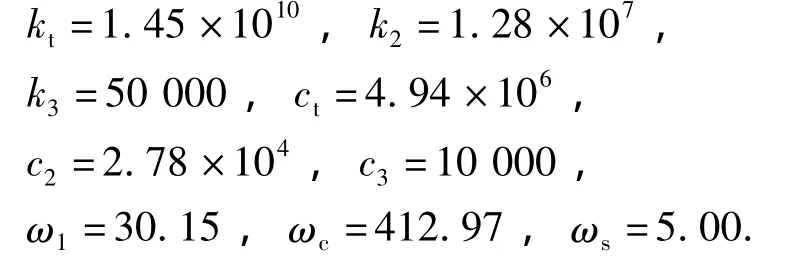
可见在系统参数正常的情况下,有
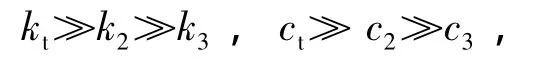
而且ω1、ω2和ω3之间隔得很远,系统难以发生剧烈自激振动.当参数都在正常范围内变化时,系统总能稳定.
从图3中可见,由于轨道和二系悬挂具有弹性,系统总会产生振动[5],而各参数会影响振动幅值的大小和衰减速度,所以对于系统物理参数已经固定的车-轨系统,主要研究的内容是如何通过调节控制器参数抑制振动,使振动的振幅减小,同时快速衰减.
瞬时最优控制从 t=0时刻开始工作(仿真2),仿真结果如图3(b)所示.可以看出振动被更好的抑制,系统起浮10 s时,悬浮气隙振幅与轨道振幅分别减少了59%、48%.
(2)二系悬挂参数改变
当车体质量取0.25m1,二系悬挂刚度取2k3,车体起浮后情况如图3(c)所示(仿真3).由于k3增加,系统稳定性减小,振动大于标准参数情况.瞬时最优控制从t=0时刻开始工作,仿真结果如图3(d)所示(仿真4),振动被有效抑制,10 s时,悬浮气隙振幅与轨道振幅分别减少了62%、94%.

图3 车-轨振动位移仿真结果Fig.3 Simulation results of vehicle-track vibration displacement
仿真中计算出的参数如下:

(3)轨道参数改变
当轨道长度取1.2L,轨道抗弯刚度取0.8EI,车体起浮后情况如图3(e)所示(仿真5).仿真中发现系统自激振动对轨道参数改变很敏感,车体-轨道振幅大幅增加,振动衰减变慢.瞬时最优控制从t=0时刻开始工作,仿真结果如图3(f)所示(仿真6),系统振动快速衰减,10 s时,悬浮气隙振幅与轨道振幅分别减少了5%、73%.
仿真中计算出的参数如下:
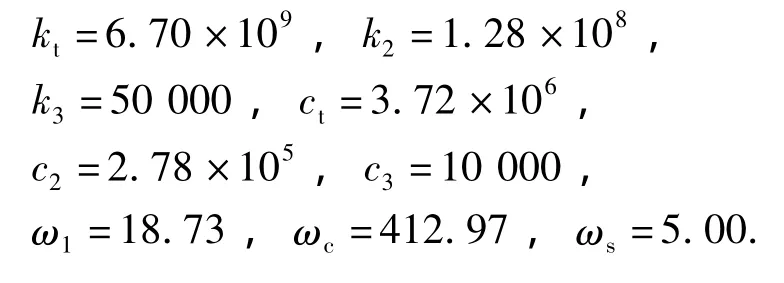
5 结束语
针对列车起浮后与轨道相互耦合发生自激振动的现象,本文通过建立模型分析了车辆-轨道系统的振动稳定性,给出了系统主要参数和稳定性的关系.研究发现,磁浮车体-悬浮架-轨道在正常参数范围内总能满足系统绝对稳定的基本条件,但系统各主要参数对于振动幅值大小、振动衰减速度有直接的影响.在系统物理参数不变的情况下,可以通过瞬时最优控制算法调节悬浮控制器参数抑制车-轨自激振动.通过数值仿真验证了系统参数与稳定性的关系以及控制方法对振动抑制的有效性.结论可供磁浮车辆-轨道系统设计参考.
致谢:西南交通大学青年教师百人计划项目资助(SWJTU2011BR052EM).
[1]赵春发.磁悬浮车辆系统动力学研究[D].成都:西南交通大学,2002.
[2]翟婉明,赵春发.磁浮车辆/轨道系统动力学(Ⅰ):磁/轨相互作用及稳定性[J].机械工程学报,2005,41(7):1-10.
ZHAI Wanming,ZHAO Chunfa.Dynamics of maglev vehicle/guideway sysystems(Ⅰ):magnet/rail interaction and system stability[J].Chinese Journal of Mechanical Engineering,2005,41(7):1-10.
[3]李莉,孟光.慢起慢落时磁浮车辆与钢轨道框架耦合共振分析[J].振动与冲击,2006,25(6):46-48.
LI Li,MENG Guang.Analysis on resonance vibration of maglev trains suspending or loading on steel track frame[J].Journal of Vibration and Shock,2006,25(6):46-48.
[4]ZHOU D F,HANSEN C H,LI J.Suppression of maglev vehicle-girderself-excited vibration usinga virtual tuned mass damper[J].Journal of Sound and Vibration,2011,330(5):883-901.
[5]施晓红,龙志强.磁悬浮车轨耦合控制系统的非线性振动特性分析[J].铁道学报,2009,31(4):38-42.
SHI Xiaohong,LONG Zhiqiang.Nonlinear vibration analysis of the maglev guideway-vehicle coupling control system[J].Journal of the China Rrailway Society,2009,31(4):38-42.
[6]洪华杰,李杰,张锰.磁浮车轨耦合系统稳定性分析[J].控制理论与应用,2006,23(3):421-428.HONG Huajie,LI Jie,ZHANG Meng.Stability analysis of magnetic levitation system with vehicle-guideway interaction[J]. Journal of Control Theory and Applications,2006,23(3):421-428.
[7]邹东升,佘龙华,张志强,等.磁浮系统车轨耦合振动分析[J].电子学报,2010,38(9):2071-2075.
ZOU Dongsheng,SHE Longhua,ZHANG Zhiqiang,et al.Maglev vehicle and guideway coupling vibration analysis[J].Acta Electronica Sinica,2010,38(9):2071-2075.
[8]黎松奇,张昆仑.磁浮列车车轨耦合振动仿真研究[J].计算机仿真,2014,31(8):137-141.
LI Songqi,ZHANG Kunlun.On simulation of track coupling vibration formaglev train[J]. Computer Simulation,2014,31(8):137-141.
[9]梁鑫,罗世辉,马卫华,等.磁浮列车单铁悬浮车桥耦合振动分析[J].交通运输工程学报,2012,12(2):32-37.
LIANG Xin,LUO Shihui,MA Weihua,et al.Coupling vibration analysis of single-magnet suspension vehiclebridge for maglev train[J]. Journal of Traffic and Transportation Engineering,2012,12(2):32-37.
[10]王洪坡,李杰.一类非自治位置时滞反馈控制系统的亚谐共振响应[J].物理学报,2007,56(5):2504-2516.
WANG Hongpo,LI Jie.Sub-harmonic resonances of the non-autonomoussystem with delayed position feedback control[J]. Acta Physica Sinica,2007,56(5):2504-2516.
[11]ZHANG Lingling,HUANG Lihong,ZHANG Zhizhou.Hopf bifurcation of the maglev time-delay feedback system via pseudo-oscillator analysis[J].Mathematical and Computer Modelling,2010,52(5/6):667-673.
[12]WANG Hui,SHEN Gang,ZHOU Jinsong.Control strategy of maglev vehicles based on particle swarm algorithm[J]. JournalofModern Transportation,2014,22(1):30-36.
[13]李云钢,常文森.磁浮列车悬浮系统的串级控制[J].自动化学报,1999,25(2):247-251.
LI Yungang,CHANG Wensen.Cascade control of an ems maglev vehicle's levitation control system[J].Acta Automatica Sinica,1999,25(2):247-251.
[14]李宏男,李忠献,祁皑,等.结构振动与控制[M].北京:中国建筑工业出版社,2005:356-359.

