Numerical Study of the Secondary Circulations in Rip Current Systems

LI Rui, and GUAN Changlong



Numerical Study of the Secondary Circulations in Rip Current Systems

LI Rui, and GUAN Changlong*

,,266100,

To investigate the mechanism of secondary circulations in rip current systems, and to explore the relationship between wave conditions and secondary circulation intensity, a series of numerical experiments is performed using coupled nearshore wave model and circulation model. In these experiments, the rip currents and secondary circulations generated above barred beaches with rip channels are simulated. A comparison experiment is conducted to investigate the formation and hydrodynamics of the secondary circulations. Model results indicate that the secondary circulations consist of alongshore flows driven by wave set-up near the shoreline, part of the feeder currents driven by the wave set-up over the bars, and onshore flows at the end of the rip channel driven by wave breaking and convection. The existence of the secondary circulation barely affects the rip current, but narrows and intensifies the feeder currents. Three groups of experiments of varying incident wave conditions are performed to investigate the relationship between wave conditions and secondary circulation intensity. The velocity of the alongshore flow of the secondary circulation is sensitive to the variation of the incident wave height and water depth. It is also found that the alongshore flow intensity is in direct proportion to the alongshore variation of the wave height gradient between the bars and the shoreline.

secondary circulation; rip current; waves; radiation stress

1 Introduction

Rip currents are strong seaward jet-like flows which are generally located at the rip channels within the surf zone. Early observations gave various crude estimations of the rip current velocity, such as 1ms−1(Shepard and Inman, 1950), 70cms−1(Short and Hogan, 1994), 50cms−1(Sonu, 1972) and 30cms−1(Huntley, 1988). Short (1999) even suggested the velocity of mega-rips exceeding 2ms−1. With such intensive flow, rip currents ‘account for more than 80% of life guard rescue efforts’ (MacMahan, 2006). Rip currents also play an important role in nearshore sediment transport (Cook, 1970; Inman, 1971; Aagaard, 1997) and morphology evolution (Sonu, 1972; Wright and Short, 1984; Brander, 1999).

Rip currents are most often observed when the waves approach shoreward at shore-normal incidence and where alongshore variations of the topography exist (Austin, 2009, 2010). For a sloping beach with alongshore sandbars which are incised by a rip channel, there is more intensive wave breaking over the sandbars than that in the rip channel due to the difference of water depth. According to Longuet-Higgins and Stewart (1964), wave break-ing induces wave set-up,, mean water level rise over the bars. Hence the resulting alongshore pressure gradient drives the water flow along the shoreward edges of the bars, which is named feeder current. The feeder currents converge in the rip channel, turn seaward and exit from the surf zone as a rip current. Then the water flows back over the bars and forms a circulation cell with the feeder current and rip current.

Besides the rip circulation cells, secondary circulation cells of counter-rotation were visualized between the bars and the shoreline in some laboratorial experiments (Borthwick and Foote, 2002; Dronen, 2002; Haller, 2002). However, it is difficult to measure them because they only exist in very shallow water. In test B of Haller’s (2002) experiments, the velocity sensors were located near the shoreline, so the secondary circulations were roughly measured for the first time. They also studied the alongshore hydrodynamics of the secondary circulations, and concluded that the secondary circulations are ‘forced by the breaking of the higher waves that have propagated through the channels’. However, due to the difficulty in installing instruments in shallow water, they could not study the dynamics of the very nearshore region (from=14m to shoreline). Besides, the wave conditions in their tests were varing, so it is hard to tell whether the existence of the secondary circulations has any effects on the rip current cells excluding the influence of waves. Moreover, even though it is commonly accepted that the secondary circulations are closely related with the wave conditions near the shoreline, a more general dimensionless relationship between waves and secondary circulations has not been studied yet.

Since there are difficulties in nearshore current observations, efforts have been made on numerical simulations for years. The first attempt to model the rip current system was carried out by Noda (1974). After that some other models were developed (, Ebersole and Dalrymple, 1980; Wu and Liu, 1985). Since these models are all depth uniformed, a common problem is that the eddy viscosity needs to be enhanced substantially to compensate for the missing dispersive mixing. The Quasi-3D Nearshore Circulation Model (SHORECIRC) combines the effects of vertical structure of the currents and bypasses this problem (Putrevu and Svendsen, 1999). It has been verified by experimental data (Haas and Svendsen, 2002; Haas, 2003), and its accuracy is comparable with that of three dimensional models (Haas and Warner, 2009). Besides, three dimensional coupled wave-current models have been developed to simulate the interaction between nearshore waves and rip currents (Kumar, 2011; Weir, 2011).

Although some researchers have also found secondary circulations in their numerical results (Farahani, 2012; Haas, 2003; Ruju, 2012; Yu and Slinn, 2003), they did not do systematical study on these circulations. In the present study, a series of numerical experiments are conducted with the Combined Refraction/Diffraction Model (REF/DIF 1) and the SHORECIRC model to investigate the dynamics of the secondary circulations more specifically, and study the effects of secondary circulations on rip currents and the relationship between wave conditions and secondary circulation intensity.

The paper is organized as follows. The numerical models used in the current study are briefly introduced in Section 2. Experimental settings and model configurations are presented in Section 3. In Section 4 a comparison experiment is conducted to reveal the mechanism of the secondary circulations and their effects on the rip current cells. Another experiment is performed in this section to study the relationship between the wave conditions and secondary circulation intensity. The conclusions are made in Section 5.

2 Numerical Models

The Nearshore Community Model (NearCoM) is an extensible, user-configurable model system for nearshore waves, circulation and sediment processes (Shi, 2005). The whole model consists of a ‘backbone’,, the master program, a wave module, a circulation module and a seabed module. All these modules are coupled to predict waves,currents,sedimenttransportandbathymetricchange in the nearshore region. Besides, each module can be run as an individual model assembled with the master program. Focusing on the waves and the circulations herein, the sediment module is switched off. The REF/DIF 1 and the SHORECIRC are chosen as the wave and circulation module respectively.

2.1 REF/DIF 1

The wave module REF/DIF 1 is a parabolic model for ocean surface wave propagation. It takes into account the effects of wave shoaling, refraction, diffraction, energy dissipation, and the Doppler shift due to currents by solving the parabolic equation initially developed by Kirby and Dalrymple (1983). The REF/DIF 1 computes the radiation stress as the wave forcing for the circulation module. The radiation stress tensorSis defined as

where the subscriptsanddenote the coordinates, and

, (2)

andδis the Kronecker delta function. Outside the surf zone,SandSare defined as

, (4)

whereis the wave height,is the water depth, andis the wave number given by the linear wave dispersion relation

whereis wave frequency. Inside the surf zone,Sare defined as

, (6)

whereis wave phase speed. The second term on the right-hand side of Eq. (6) represents the radiation stress induced by the presence of the surface roller (Svendsen, 1984a, 1984b). The expression ofSis the same as Eq. (4). Cubic spline function is used to smooth the radiation stress around breaking line to avoid unrealistic gradients.

2.2 SHORECIRC

The circulation module SHORECIRC is a quasi-3D model. Although its computing scheme is two dimensional (abbreviated to 2D), it includes the effect of the vertical variation of the currents, which bypasses the problem that the eddy viscosity needs to be enhanced substantially to compensate for the missing dispersive mixing for most of the 2D models. The derivation of the vertical variation of currents follows the method of Putrevu and Svendsen (1999). The governing equations of SHORECIRC are

, (8)

where`represents time averaged sea surface elevation,the total volume flux,Vthe depth-varying part of the current velocity, uw the wave-induced velocity,0the still water depth,andthe surface and the bottom shear stress respectively,the radiation stress, andthe turbulent Reynold’s stresses. Details about governing equations and turbulence model could be found in Haas(2003).

3 Experimental Setup

Firstly, a comparison experiment (abbreviated to Exp. 1) is conducted to investigate the formation and hydrodynamics of secondary circulations. Two kinds of topography settings as shown in Fig.1 are used in case A and case B respectively. The one used in case A is a sloping beach (bottom slope being 1/30) with a rip channel and two alongshore underwater bars. The edges of the bars near the rip channel are smoothed in order to limit wave reflection. The other topography setting used in case B is of the same pattern as that used in case A, except that the water bottom between the shoreline and the bars is flat and deeper (0.53m) and the distance between them is larger (29m). The topography in case B is designed to eliminate the secondary circulations, and to insure the similarity of the rip currents in the two cases. Incident wave conditions of the two cases are the same (Table 1). The plan view of the topography in both cases is shown in Fig.2. The computing domain is a rectangular basin of 80m in width and 80m (100m) in length in case A (B). Waves enter from the left boundary and propagate rightward to the shoreline. The incoming side of the basin is an absorbing/generating boundary which could absorb most of the return flow, the two lateral sides are periodic boundaries, and the shoreline is set as no-flux boundary.

Secondly, another experiment is conducted to investigate the relationships between wave conditions and secondary circulation intensity. Incident wave height, incident wave period and water depth are varied respectively in three cases to cover as much scenario as possible because secondary circulations do not appear in all the rip current systems. The topographies used in the experiments are the same as the one used in case A of Exp.1. Details of the incoming wave conditions are shown in Table 1.

For all the experiments, the model grid spacing Δ=1m and Δ=1m, and the computing time step Δ=0.037s which corresponds to a Courant number of 0.4. The time interval of data exchange between REF/DIF 1 and SHORECIRC is set to 2s. The SHORECIRC is configured as: bottom friction coefficientf=0.02, eddy viscosity coefficientν=0.08,=0.08, and the Smagorinksy eddy viscosity coefficientC=0.2. These parameters are all variable and configured according to Svendsen’s (2003) recommendations. All the simulations are computed for 1000s when the current fields are steady. The SHORECIRC runs in 2-dimensional mode (–), so the ‘velocity’ and ‘forces’ mentioned in this paper are all depth-averaged quantities.

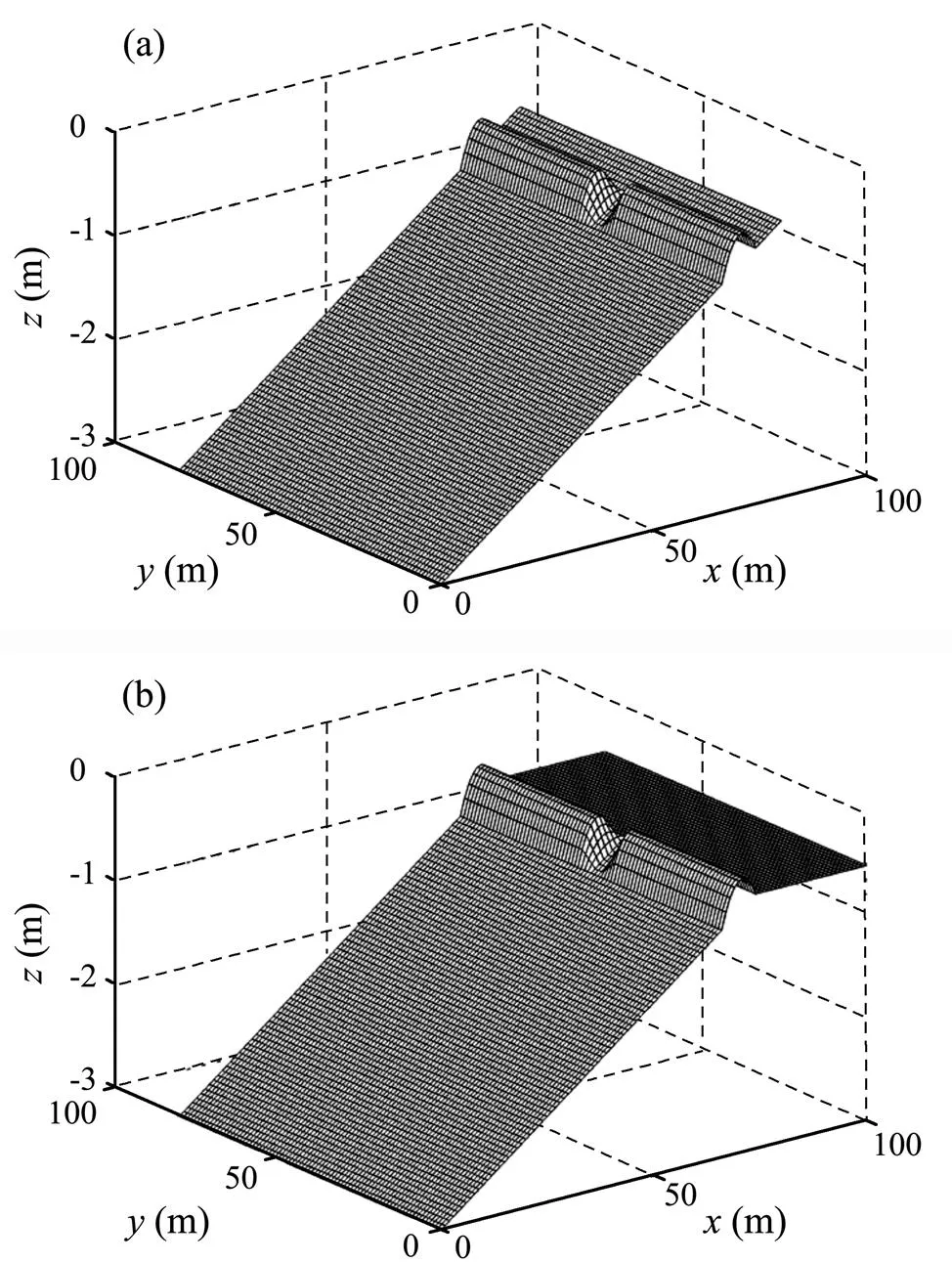
Fig.1 Side view of the topographies used in case A (a) and case B (b) of Exp. 1.

Table 1 Wave conditions and water depth setup of the experiments

Notes:0is the incident wave height,0is the incident wave period, andDis the water depth at the bar crest.

Fig.2 Plan view of the model domain. Ltrough is the distance between the bars and the shoreline, which equals to 9m (29m) in case A (B) of Exp. 1. Waves enter the domain from the left side, and the shoreline is located at the right side. The shading areas represent the bar regions.

4 Results

4.1 Hydrodynamics of Secondary Circulations

The computed circulations of cases A and B in Exp. 1 are shown in Fig.3. It can be seen that the patterns of the current field of the two cases are different. A dipole of secondary circulations appears between the bars and the shoreline in case A, but basically disappears in case B. Fig.4 shows the difference of the velocity magnitude between case A and case B

whereu,uare the cross-shore velocity components in case A and case B respectively, andvandvare the alongshore velocity components in case A and case B respectively. It can be seen that the rip currents are basically the same in the two cases, and the difference of the current fields mainly appears in three regions: 1) near the shoreline (=78m, difference being most obvious), 2) near the shoreward edges of the bars (=74m), and 3) along the centerline of the rip channel (=39m).

The alongshore depth-averaged radiation stress (abbreviated to RS) gradient

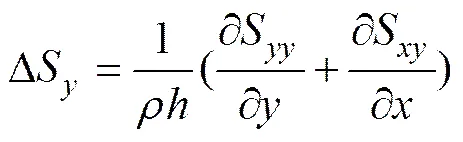
and the alongshore hydrostatic pressure gradient

, (11)

along the=78m and=74m sections, and the cross-shore depth-averaged RS gradient

and the cross-shore pressure gradient

, (13)

along the=39m section, are respectively studied below.

The alongshore RS gradient ΔSand the pressure gradient ΔPalong the=78m section are shown in Fig.5. It can be seen that the pressure gradient in case A is much larger than the RS gradient, which drives the water flows along the shoreline. When waves propagate through the rip channel, the wave breaking near the shoreline induces wave set-up,, high water level, which causes large pressure gradient along the shoreline. In case B there is barely wave breaking after the waves propagate through the rip channel, so the pressure gradient is much smaller.

The ΔSand ΔPalong the=74m section are shown in Fig.6. It can be seen that the pressure gradient in case A is larger than that in case B. This is because in case A the water depth and the space between the bars and the shoreline are both smaller, hence the water is more likely to accumulate in this area than it is in case B. So the larger pressure gradient in case A drives stronger feeder currents.

Fig.3 Currents vectors of case A (a) and case B (b) in Exp. 1. Background color represents the topography (unit: m). Rectangles represent the ranges of the bars. The incident wave conditions in both cases are the same and listed in Table 1.

The cross-shore RS gradient ΔSand the pressure gradient ΔPalong the=39m section are shown in Fig.7. In case A the pressure gradient near the shoreline (=74m–80m) oscillates somewhat due to boundary effect. The mean value of the resultant force in this range is 5×10−3 ms−2,, the onshore RS gradient induced by wave breaking plays a part in driving the onshore flow. Besides, it canbe seen that the convective termin the region=74m–76m is positive,, the convection also plays a part in driving the onshore flow. This is probably because when the feeder currents converge in the channel, the water is partly transferred onshore to compensate the divergence of the alongshore currents.

Fig.4 Velocity difference between case A and case B in Exp.1 (unit: ms−1). Rectangles represent the ranges of the bars.

Fig.5 Alongshore variation of RS gradient ΔSy (red line), pressure gradient ΔPy (blue line) and their resultant force (black line) near the shoreline (x=78m) in case A (a) and case B (b).

Fig.6 Alongshore variation of RS gradient ΔSy (red line), pressure gradient ΔPy (blue line) and their resultant force (black line) near the shoreward edges of the bars (x=74m) in case A (a) and case B (b).

Fig.7 Cross-shore variation of RS gradient ΔSx (red line), pressure gradient ΔPx (blue line) and their resultant force (black line) along the centerline of the rip channel (y=39m) in case A (a) and case B (b). The green line in panel (a) represents the cross-shore variation of the convective terms in case A.

4.2 Effects of Secondary Circulations on Rip Current Cells

To investigate the effects of the secondary circulations on rip current cells, the velocity sections of the rip currents and feeder currents of the two cases in Exp. 1 are compared.

Fig.8 shows the cross section and longitudinal section of the rip current velocity. The rip current velocities are basically the same in case A and case B (the difference of the rip current velocity is only of O(10−3ms−1)), meaning that the rip current is barely affected by the presence of the secondary circulations in this experiment.

Fig.9 shows the cross section and longitudinal section of the feeder current velocity. Clearly there are stronger feeder currents in case A. The difference of the maximum feeder current velocities between the two cases is 0.0186ms−1. On one hand, as illustrated before, the slope bottom topography in case A induces larger alongshore pressure gradient; on the other hand, the width of the feeder currents is narrowed by the presence of the secondary circulations. Since the rip current, feeder current and the back-flow over the bar form a closed cell and the rip current velocity in case A is the same as that in case B, the velocity of the feeder current should be larger in case A to keep the conservation of mass flux.

Fig.8 Cross-shore velocity component in case A (blue line) and case B (red line) along the section y=39m (a) and x=65m (b).

Fig.9 Alongshore velocity component in case A (blue line) and case B (red line) along the section x=73m (a) and y=25m (b).

4.3 Relation Between Waves and Secondary Circulations

It can be seen from Figs.3 and 4 that the alongshore flows are the most obvious character of the secondary circulations. Hence we focus on the alongshore flows in this section. The maximum alongshore flow velocity near the shorelinesec_maxis used to represent the secondary circulation intensity. The variations ofsec_maxwith incident wave conditions are shown in Fig.10. In case C, as incident wave height increases,sec_maxincreases first due to the increasing energy transferred from wave to current near the shoreline. As incident wave height keeps increasing, the rip current becomes strong, which would dissipate the wave energy in the channel rather than near the shoreline, sosec_maxdecreases. In case D, as incident wave period increases, the variation ofsec_maxis small and irregular. In case E, as water depth increases, the rip current intensity decreases, so more waves can propagate through the rip channel and break near the shoreline. Hencesec_maxincreases with increasing water depth. But as water depth keeps increasing, there is no wave breaking over the bars. So the waves are basically homogenous alongshore, which induces smallsec_max.

Since the secondary circulations are mainly due to waves penetrating the rip channel and finally breaking near the shoreline, the alongshore flow should be closely related with the wave forcing between the bars and the shoreline. Longuet-Higgins and Stewart (1964) indicated that the wave set-up is induced by the cross-shore changes of radiation stress following the relation

Besides, it can be seen from Eqs. (3) and (4) that the radiation stress is mainly influenced by the variation of wave height. So the wave set-up can be roughly reflected by the wave height gradient in the cross-shore direction Δx. Since the wave set-up gradient along the shoreline causes the alongshore flow, the difference of Δxin the alongshore direction Δ(Δx) may reflect the intensity of the alongshore flow of the secondary circulations. Here the difference Δ(Δx) is defined as

where the subscript ‘channel’ means ‘along the center line of the rip channel (=40m)’, ‘bar’ means ‘along the cross-shore intersection of the bars (=60m)’, ‘1’ means ‘at the onshore edge of the bars (=75m)’, and ‘2’ means ‘near the shoreline (=79m)’. The maximum alongshore flow velocity near the shorelinesec_maxis used to represent the secondary circulation intensity. Following the approach that Haller(2002) (abbreviated to H02) used to investigate the relations between incident waves and rip currents, wave phase speed and water depth are used to normalize the velocity and wave height respectively. Thus the dimensionless velocitysec_dimis defined as

, (16)

whereis the water depth at the onshore edge of the bars, and the dimensionless wave height is defined as

Thedim_secanddim_secin Exp. 2 are calculated and their relations are shown in Fig.11. It can be seen that basicallydim_secincreases with increasingdim_sec, in other words, the intensity of the secondary circulation might be reflected by the alongshore variability of the wave height gradient. Thedim_secanddim_secof the two cases in Exp. 1 and the Test B of H02’s experiment are also plotted in Fig.11. It can be seen that both the results of Exp. 1 and the result of H02’s experiment basically follow the increasing trend. It is worthy to note that thedim_secof H02’s experiment is smaller than that from linear fitting, probably because the real maximum alongshore velocity was not sampled due to limited measurements near the shoreline in their experiments.

Fig.10 Variation of with incident wave height (a), incident wave period (b) and water depth at the bar crest (c).

Fig.11 Vdim_secvs.Hdim_sec in cases A–E and H02’s experiment (asterisks). Solid line represents the least-squares linear fit for the data of cases C–E.

5 Conclusion and Discussion

With the coupled nearshore wave model REF/DIF 1 and circulation model SHORECIRC, a series of numerical experiments has been performed over barred beaches with rip channels to investigate the mechanism of secondary circulations and the relationship between waves and secondary circulations. Comparison experiments show that the secondary circulation consists of the alongshore flow near the shoreline, part of the feeder current and the onshore flow at the end of the rip channel. The alongshore flow near the shoreline is driven by the wave set-up there, the feeder current is driven by the wave set-up over the bars, and the onshore flow is driven by wave breaking and convection. Velocity sections indicate that the existence of the secondary circulations barely affects the rip current, but narrows and intensifies the feeder currents. The relationship between the wave conditions and the alongshore flow of the secondary circulation is also investigated. Model results indicate that the alongshore flow velocity increases first, and then decreases with increasing incident wave height or with increasing water depth, but there is not a clear relation between the alongshore flow and the incident wave period. The velocity of the alongshore flow is in direct proportional to the alongshore variation of the wave height gradient between the bars and the shoreline. However, it is worthy to note that the gradient of wave height may not be the only reason for the secondary circulation. Difference of wave period or wave number probably could also affect the intensity of the secondary circulations. So a more precise dimensionless wave parameter would be worth developing in future studies.

Acknowledgements

We would like to thank Dr. Fengyan Shi for his unselfish help with the model configurations. The research is supported by China’s Public Science and Technology Research Funds Projects of Ocean (No. 200905013-4) and by Ministry of Science and Technology of China (No. 2011BAC03B01).

Aagaard, T., Greenwood, B., and Nielsen, J., 1997. Mean currents and sediment transport in a rip channel., 140 (1-2): 25-45.

Austin, M., Scott, T., Brown, J., Brown, J., and MacMahan, J., 2009. Macrotidal rip current experiment, circulation and dynamics., 56: 24-28.

Austin, M., Scott, T., Brown, J., Brown, J., MacMahan, J., Masselink, G., and Russell, P., 2010. Temporal observations of rip current circulation on a macro-tidal beach., 30 (9): 1149-1165.

Borthwick, A. G. L., and Foote, Y. L. M., 2002. Wave-induced nearshore currents at a tri-cuspate beach in the UKCRF., 154 (4): 251-263.

Brander, R. W., 1999. Field observations on the morphodynamic evolution of a low-energy rip current system., 157 (3-4): 199-217.

Cook, D. O., 1970. The occurrence and geologic work of rip currents off southern California., 9 (3): 173-18 6.

Dronen, N., Karunarathna, H., Fredsoe, J., Sumer, B. M., and Deigaard, R., 2002. An experimental study of rip channel flow., 45 (3-4): 223-238.

Ebersole, B. A., and Dalrymple, R. A., 1980. Numerical modeling of nearshore circulation. In:. No. 17, Sydney, Australia.

Farahani, R. J., Dalrymple, R. A., Hérault, A., and Bilotta, G., 2012. SPH modeling of mean velocity circulation in a rip current system. In:. No. 33, Santander, Spain.

Haas, K. A., and Svendsen, I. A., 2002. Laboratory measurements of the vertical structure of rip currents., 107 (C5): 1-19.

Haas, K. A., and Warner, J. C., 2009. Comparing a quasi-3D to a full 3D nearshore circulation model: SHORECIRC and ROMS., 26 (1-2): 91-103.

Haas, K. A., Svendsen, I. A., Haller, M. C., and Zhao, Q., 2003. Quasi-three-dimensional modeling of rip current systems., 108 (C7): 1-21.

Haller, M. C., Dalrymple, R. A., and Svendsen, I. A., 2002. Experimental study of nearshore dynamics on a barred beach with rip channels., 107 (C6): 1-21.

Huntley, D. A., Hendry, M. D., Haines, J., and Greenidge, B., 1988. Waves and rip currents on a Caribbean pocket beach, Jamaica., 4 (1): 69-79.

Inman, D. L., Tait, R. J., and Nordstrom, C. E., 1971. Mixing in the surf zone., 76 (15): 3493-3514.

Kirby, J. T., and Dalrymple, R. A., 1983. A parabolic equation for the combined refraction and diffraction of Stokes waves by mildly varying topography., 136: 453-466.

Kumar, N., Voulgaris, G., and Warner, J. C., 2011. Implementation and modification of a three-dimensional radiation stress formulation for surf zone and rip-current applications., 58 (12): 1097-1117.

Longuet-Higgins, M. S., and Stewart, R. W., 1964. Radiation stress in water waves: A physical discussion, with applications.h, 11 (4): 529-562.

MacMahan, J. H., Thornton, E. B., and Reniers, A. J. H. M., 2006. Rip current review., 53 (2-3): 191-208.

Noda, E. K., 1974. Wave-induced nearshore circulation., 79 (27): 4097-4106.

Putrevu, U., and Svendsen, I. A., 1999. Three-dimensional dispersion of momentum in wave-induced nearshore currents., 18 (3): 409-427.

Ruju, A., Higuera, P., Lara, J. L., Losada, I. J., and Coco, G., 2012. Rip currents on a barred beach. In:. No. 33, Santander, Spain.

Shepard, F. P., and Inman, D. L., 1950. Nearshore water circulation related to bottom topography and refraction., 31 (2): 196-212.

Shi, F., Kirby, J. T., Newberger, P., and Haas, K., 2005. NearCoM master program, Version 2005.4: User’s manual and module integration. University of Delaware.

Short, A. D., 1999.. John Wiley and Sons, 392pp.

Short, A. D., and Hogan, C. L., 1994. Rip currents and beach hazards: Their impact on public safety and implications for coastal management., 12: 197-209.

Sonu, C. J., 1972. Field observation of nearshore circulation and meandering currents., 77 (18): 3232-3247.

Svendsen, I. A., 1984a. Wave heights and set-up in a surf zone., 8 (4): 303-329.

Svendsen, I. A., 1984b. Mass flux and undertow in a surf zone., 8 (4): 347-365.

Svendsen, I. A., Haas, K., and Zhao, Q., 2003. Quasi-3D nearshore circulation model SHORECIRC. User’s Manual. University of Delaware, 64pp.

Weir, B., Uchiyama, Y., Lane, E. M., Restrepo, J. M., and McWilliams, J. C., 2011. A vortex force analysis of the interaction of rip currents and surface gravity waves., 116 (C5): 1-16.

Wright, L. D., and Short, A. D., 1984. Morphodynamic variability of surf zones and beaches: A synthesis., 56 (1-4): 93-118.

Wu, C., and Liu, P., 1985. Finite element modeling of nonlinear coastal currents., 111 (2): 417-432.

Yu, J., and Slinn, D. N., 2003. Effects of wave-current interaction on rip currents., 108 (C3): 1-19.

(Edited by Xie Jun)

DOI 10.1007/s11802-015-2361-2

ISSN 1672-5182, 2015 14 (1): 9-16

© Ocean University of China, Science Press and Springer-Verlag Berlin Heidelberg 2015

(April 7, 2013; revised April 22, 2013; accepted July 11, 2014)

* Corresponding author. Tel: 0086-532-66782192 E-mail:clguan@ouc.edu.cn