一类利用从属关系定义的复数阶双单叶函数类的系数问题
都俊杰,邹发伟,秦川,冯建中
一类利用从属关系定义的复数阶双单叶函数类的系数问题
都俊杰1,邹发伟1,秦川1,冯建中2
(1.长江大学工程技术学院,湖北荆州434020;2.长江大学信息与数学学院,湖北荆州434000)
利用Salagean算子和从属关系定义一类复数阶双单叶函数类MΣ(n,b,β;h),利用从属定理研究得到它的系数|a2|和|a3|的上界,并讨论一些应用广泛的函数类,扩展了一些已有结论,在证明方法上有了较大的变化.
解析函数;双单叶函数;从属;Salagean算子
本文用C表示复数集,N表示正整数集,N0表示非负整数集.记A表示单位圆盘U={z∈C:|z|<1}内解析且具有如下展开式的函数族
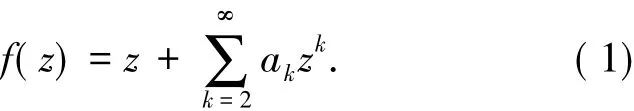
对于f(z)∈A,G.S.Salagean[1]定义Salagean微分算子D如下:

容易验证
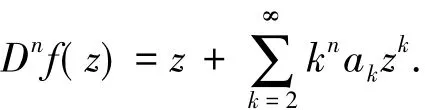
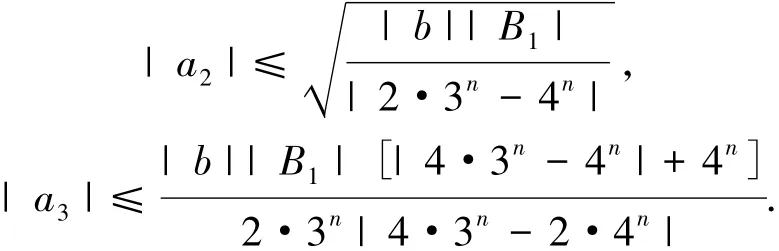
记S表示A中满足(1)式且单叶的子族.设f(z)和g(z)在U内解析,称f(z)从属于g(z)[2],记作f(z) 众所周知,对任意具有(1)式形式的函数f(z)∈S均存在逆函数f-1,定义为 其中 函数f(z)∈A称为U内的双单叶函数当且仅当f(z)和f-1(w)均为U的单叶函数,现记Σ表示U具有(1)式形式的双单叶函数族[11].文献[12-14]引入了双单叶函数族Σ中的α阶强星形函数类S*Σ(α)和α阶凸函数类KΣ(α)如下: 其中,0≤α<1,g(w)=f-1(w).自从H.M.Srivastava等[11]研究了双单叶函数族的系数性质后,就有越来越多的学者开始关注并定义了众多双单叶函数子类,通过研究系数|a2|和|a3|的非精确上界估计(详见文献[15-22]),其结果已运用于不动点理论、解析函数边值问题、逆函数等进行研究,详见文献[23-25]. 设h:U→C为满足下列条件的凸单叶函数假设h(z)具有下列展开式 f(z)∈Σ由(1)式给出,称f(z)∈MΣ(n,b,β;h),若f(z)及其逆函数g(w)=f-1(w)满足从属关系: 其中,n∈N0,β∈(,b为任意非零复数. 1)取β=0,f(z)∈MΣ(n,b,0;h)满足 函数类MΣ(n,b,0;h)由熊良鹏等[26]引入并研究. 若β=0,f(z)∈MΣ(n,b,0,α),则f(z)满足 函数类MΣ(n,b,0,α)由邓琴[27]引入并研究了它的系数估计.函数类MΣ(0,b,0,α)为复数阶双单叶解析星象函数,由Q.Deng[28]引入,并由D.Erhan[29]研究. 函数类MΣ(0,1,β,α)由H.Orhana等[30]引入.若β =0,MΣ(0,1,0,α)=(α)为α阶星象函数类,由X.F.Li等[31]定义并研究. 若β=0,MΣ(1,1,0,α)=CΣ(α)为α阶凸函数类,由D.A.Brannan等[32]定义并研究. 为了得到结论,需要用到下面引理. 引理1.1[33]若p∈P,其中P表示U中的正实部解析函数族,则|pk|≤2,k=1,2,…,其中 引理1.2[34]设函数φ(z)为U内由下式定义的凸函数 设函数ψ(z)为U内由下式定义的全纯(或解析)函数 若ψ(z)<φ(z),则有 定理1.3若由(1)式定义的函数f(z)∈MΣ(n,b,β;h),则有: 证明由(2)式,存在2个正实部函数p(z),q(z) 其中 通过比较(3)和(4)式两边z2和z3的系数得到 和 由(5)和(7)式容易得到 由(6)式加上(8)式得 由于p(z),q(z)∈h(U),利用引理1.2有 将(10)式运用于(9)式有 为了得到|a3|的系数估计,将(6)式减去(8)式得 再将(9)式代入(11)式得到 再次对系数p2和q2利用引理1.2得 推论2.1[26]由(1)式定义的f(z)∈MΣ(n,b,0;h),则有: 证明在定理1.3中令β=0即可得到结论. 推论2.2由(1)式定义的f(z)∈MΣ(n,b,β; A,B),则有: 证明由于 在推论2.1中令B1=A-B即可得到结论. 推论2.3由(1)式定义的f(z)∈MΣ(n,b,β,α),则有: 证明在推论2.2中令A=-1,B=1-2α,即可得到结论. 推论2.4[30]由(1)式定义的f(z)∈MΣ(0,1,β,α),则有: 证明由于 且B1=A-B=2(1-α),在定理1.3中n=0,b=1,B1=2(1-α),即可得到结论. 推论2.5[28]由(1)式定义的f(z)∈MΣ(0,1,0,α),则有: 证明在推论2.4中令β=0即可得到结论. 推论2.6由(1)式定义的f(z)∈MΣ(1,1,β,α),则有: 证明由于 且B1=A-B=2(1-α),在定理1.3中令n=1,b=1,B1=2(1-α),即可得到结论. 推论2.7[32]由(1)式定义的f(z)∈MΣ(1,1,0,α),则有: 证明在推论2.6中令β=0即可得到结论. 致谢长江大学科研发展基金(2013CJY01)和长江大学工程技术学院科技创新基金(15J0802)对本文给予了资助,谨致谢意. [1]SALAGEAN G S.Subclasses of univalent functions[C]//Lect Notes Math,1013.New York:Springer-Verlag,1983:362-372. [2]MILLER S S,MOCANU P T.Differential Subordinations[C]//Monographs and Textbooks in Pure and Applied Mathematics.New York:Marcel Dekker,2000. [3]MILLER S S,MOCANU P T.Differential Subordinations,Theory and Applications[M].New York:Marcel Dekker,2000. [4]SRIVASTAVA H M,OWA S.Univalent Functions[M].New York:John Wiley&Sons,1989. [5]SRIVASTAVA H M,OWA S.Current topics in Analytic Function Theory[M].Singapore:World Scientific,1992. [6]IBRAHIM R W,DARUS M.On subordination theorems for new classes of normalize analytic functions[J].Appl Math Sci,2008,56:2785-2794. [7]ALI R M,CHO N E,RAVICHANDRAN V,et al.Differential subordination for functions associated with the lemniscate of Bernoulli[J].Taiwanese J Math,2012,16(3):1017-1026. [8]SRIVASTAVA H M,BANSAL D.Coefficient estimates for a subclass of analytic and bi-univalent functions[J].J Egyptian Math Soc,2015,23(2):242-246. [9]SINGH S,GUPTA S,SINGH S.Differential subordination and superordination theorems for certain analytic functions[J].General Mathe,2010,18(2):143-159. [10]IBRAHIM R W,DARUS M,MOMANI S.Subordination and superordination for certain analytic functions containing fractional integral[J].Survey in Math and Its Applications,2009,4:111-117. [11]SRIVASTAVA H M,MISHRA A K,GOCHHAYAT P.Certain subclasses of analytic and bi-univalent functions[J].Appl Math Lett,2010,23(10):1188-1192. [12]BRANNAN D A,TAHA T S.On some classes of bi-univalent functions[J].J Math Anal Appl,1985,2:18-21. [13]XU Q H,XIAO H G,SRIVASTAVA H M.A certain general subclass of analytic and bi-univalent functions and associated coefficient estimate problems[J].Appl Math Comput,2012,218(23):11461-1465. [14]ALI R M,LEE S K,RAVICHANDRAN V,et al.Coefficient estimates for bi-univalent Ma-Minda starlike and convex functions[J].Appl Math Lett,2012,25(3):344-351. [15]李小飞,秦川.一类利用从属关系定义的双单叶函数类[J].四川师范大学学报(自然科学版),2014,37(4):511-514. [16]熊良鹏.双单叶星形和凸函数的系数边界[J].西南师范大学学报(自然科学版),2015,40(6):5-10. [17]秦川,李小飞.一类利用复合算子函数定义的解析函数类的包含性质[J].四川师范大学学报(自然科学版),2015,38(3):376-380. [18]DENIZ E,CAGLAR M,ORHAN H.Second Hankel determinant for bi-starlike and bi-convex functions of order β[J].Appl Math Comput,2015,271:301-307. [19]PENG Z G,HAN Q Q.On the coefficients of several classes of bi-univalent functions[J].Acta Math Sci,2014,B34(1):228-240. [20]AKIN G,EKER S S.Coefficient estimates for a certain class of analytic and bi-univalent functions defined by fractional derivative[J].Comptes Rendus Math,2014,352(12):1005-1010. [21]SRIVASTAVA H M,BULUT S,CAGLAR S,et al.Coefficient estimates for a general subclass of analytic and bi-univalent functions[J].Filomat,2013,27(5):831-842. [22]SUN Y,JIANGA Y P,RASILA A.Coefficient estimates for certain subclasses of analytic and bi-univalent functions[J].Filomat,2015,29(2):351-360. [23]DZIOK J.Classes of multivalent analytic and meromorphic functions with two fixed points[J].Fixed Point Theory and Applications,2013,2013(1):1-18. [24]KUMAR S.A Short suvery of the development of fixed point theory[J].Survey Math and Its Applications,2013,8:91-101. [25]NARANG T D.A fixed point theorem for nonexpansive compact self-mapping[J].Annales UMCS Mathematica,2014,68(1):43-47. [26]熊良鹏,田琳,李小飞.基于Salagean算子的bi-单叶函数系数估计[J].数学的实践与认识,2015,45(3):219-223. [27]邓琴.具有复数阶的某类解析函数[J].杭州电子科技大学学报,2010,30(3):88-90. [28]DENG Q.Certain subclass of analytic functions with complex order[J].Appl Math Comput,2009,208:359-362. [29]ERHAN D.Certain subclasses of bi-univalent functions satisfying subordinate conditions[J].J Classical Anal,2013,2(1):49-60. [30]ORHANA H,MAGESHB N,BALAJIC V K.Initial coefficient bounds for a general class of bi-univalent functions[J].Filomat,2015,25(6):1259-1267. [31]LI X F,WANG A P.Two new subclasses of bi-univalent functions[J].Int Math Forum,2012,7:1495-1504. [32]BRANNAN D A,TAHA T S.On some classes of of bi-univalent functions[J].Studia Univ Babes-Bolyai Math,1986,31(2):70-77. [33]POMMERENKAE C.Univalent Functions[M].Gottingen:Vandenhoeck Ruprecht,1975. [34]XU Q H,SRIVASTAVA H M,LI Z.A certain subclass of analytic and close-to-convex functions[J].Appl Math Lett,2011,24 (3):396-401. Coefficient Problem of a New Subclass of Bi-univalent Functions with Complex Order Defined by Subordinary DU Junjie1,ZOU Fawei1,QIN Chuan1,FENG Jianzhong2 In this paper,the authors introduce a new subclass MΣ(n,b,β;h)of bi-univalent functions with complex order defined by subordinary.The purpose is to obtain the estimates on the coefficients bounds|a2|and|a3|.At the same time,some families with wide application are also discussed.The results extend the recent works.There are few changes in the method of proof. analytic functions;bi-univalent;subordinary;Salagean operater O174.51 A 1001-8395(2016)03-0344-05 10.3969/j.issn.1001-8395.2016.03.008 (编辑李德华) 2015-08-26 湖北省自然科学基金(2013CFAO053)和湖北省教育厅科研项目(B2013281) 都俊杰(1981—),女,讲师,主要从事数理统计和泛函分析的研究,E-mail:dujunjie0420@163.com 2010 MSC:30C45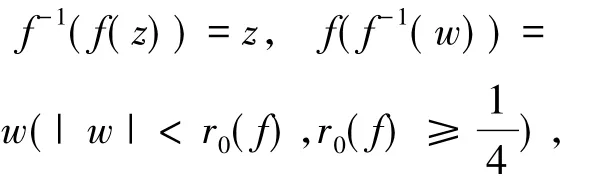



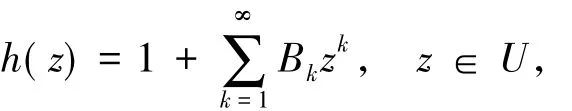
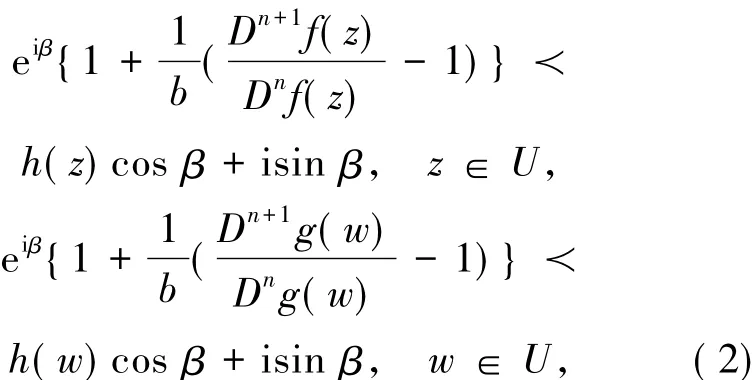
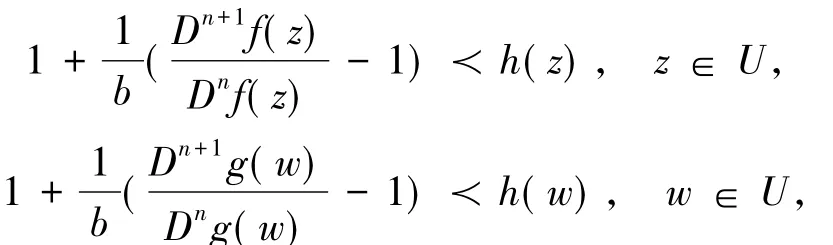
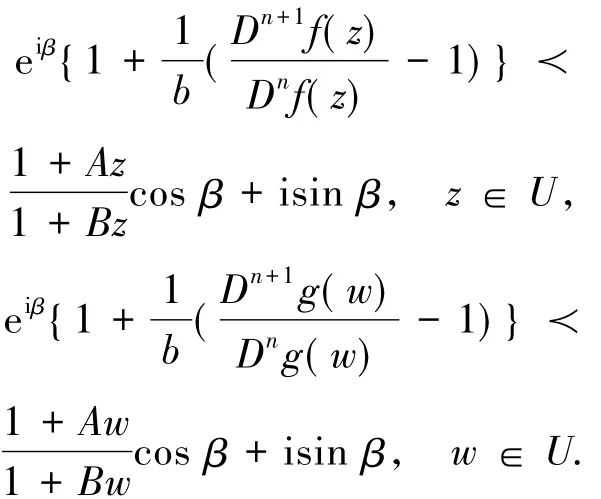

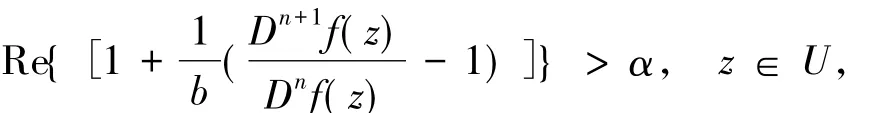


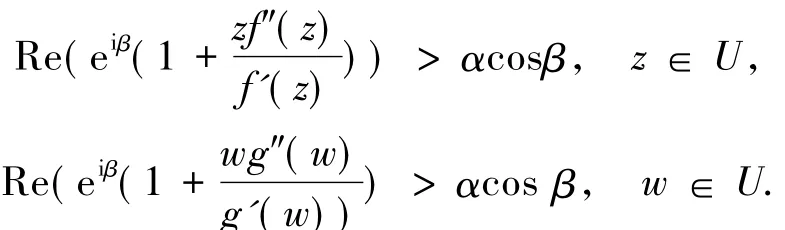
1 主要结论
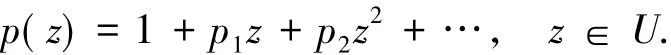
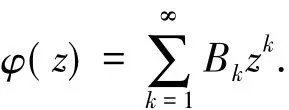


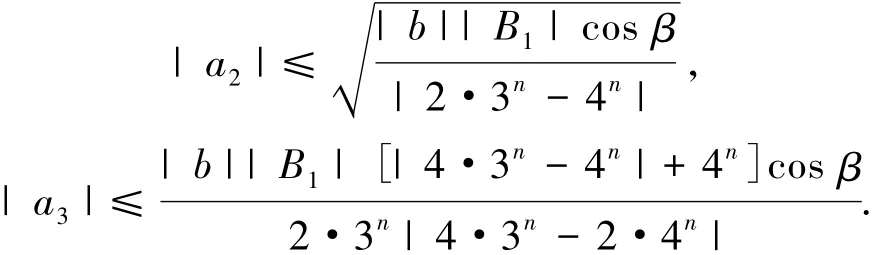



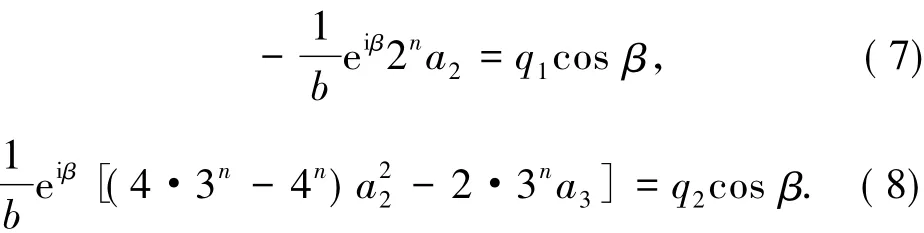




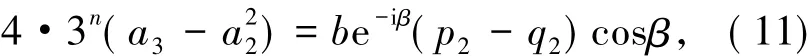

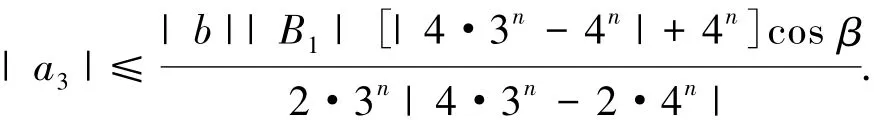
2 推论


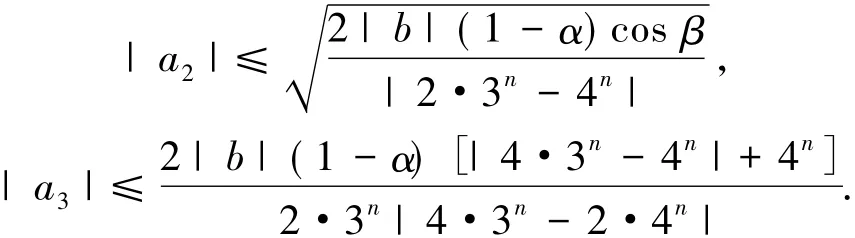
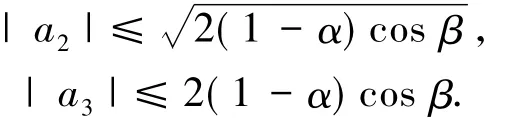
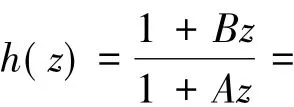
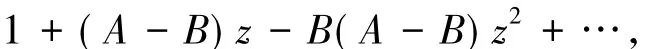
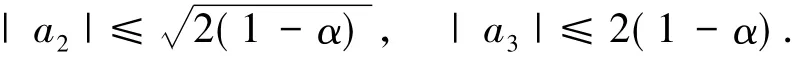
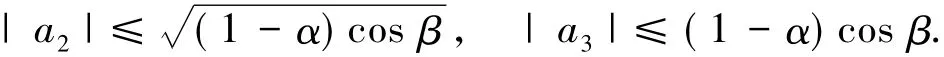
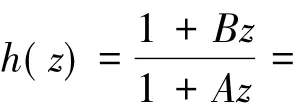
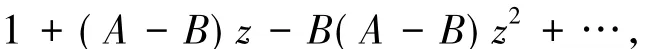

(1.College of Engineering and Technology,Yangtze University,Jingzhou 434020,Hubei; 2.School of Information and Mathematic,Yangtze University,Jingzhou 434000,Hubei)

