带位势的弱F-调和映照的单调公式
韩英波, 方联银, 李 静
(信阳师范学院 数学与信息科学学院, 河南 信阳 464000)
0 引言
设F:[0,)→[0,)是二阶可导函数,且在[0,)上F(0)=0,F′(t)>0.u:(Mm,g)→(Nn,h)是光滑映照.ARA[1]介绍了如下泛函:
这里|du|是映照u的Hilbert-Schmidt模长,其表达式如下:

其中{e1,…,em}是黎曼流形(M,g)上局部正交标架.称u是弱F-调和映射,若对于任意一个紧致变分区域,u都是F-能量泛函的临界点.目前已有很多关于F-调和映照的研究结果[2-6].
FARDON和RATTO[7]提出一个具体种类的广义调和映照——带位势的调和映照.他们发现由于位势的存在,带位势的调和映照具有一些与普通调和映照不同的性质.之后,又有许多带位势的调和映照[8,9]及带位势的p-调和映照[10]的相关结果.罗洋[11]给出了下面泛函:
其中H是Nn上的光滑函数.若对于任意紧致变分,u都是泛函EF,H(u)的变分的临界点,则称其为带位势的F-调和映照.利用应力-能量张量的方法,文献[11]得到了一些单调公式及刘维尔型定理,并研究了以Rm+1中紧致超曲面为出发流形或目标流形的带位势的F-调和映照的稳定性.

任何M的向量场X都有du(X)∈Γ(u-1TN).若X在M的内部具有紧致支撑集,则
du(X)∈Γ0(u-1TN).
定义1 设映照u:(Mm,g)→(Nn,h)是光滑映照.若对于任何X∈Γ0(TM),都有Ddu(X)EF,H(u)=0,则称u为泛函EF,H(u)的带位势H的弱F-调和映照.
注1 由带位势H的F-调和映照和上面的定义1可知:带位势H的F-调和映照必为带位势H的弱F-调和映照,即带位势H的弱F-调和映照是带位势H的F-调和映照的推广.
1 预备知识
τF,H(u)=τF(u)+NH°u,
其中
τ(u)=-δ(du).
引理1[11](第一变分公式) 设u:M→N是光滑映射,则有:
(1)
其中ψ=Γ0(u-1TN).
设u:M→N是从M到N的带位势H的弱F-调和映照.由引理1和带位势的弱F-调和映照定义可知:
即
(2)
其中X∈Γ0(TM).
引理2[2,12]若T是对称的(0,2)型张量场,X是一个向量场,则有:
(4)
其中LX是相对度量g沿X方向的李导数.
ARA[1]引入了映射u关于F-能量泛函EF(u)的应力能量张量SF(u)
(5)
引理3[1]设u:(M,g)→(N,h)是从(M,g)到(N,h)的光滑映照,则有:
(divSF)(X)=-h(τF(u),du(X)),
(6)
其中X∈Γ(TM).
若u是带位势的弱F-调和映照,由式(2)和式(6)可得:

(7)
其中X∈Γ0(TM).由T=SF可得对于任意X∈Γ(TM)都有:

(8)
文献[11]中的映射u关于F-能量泛函EF,H(u)的应力能量张量SF,H(u)为:
(9)
引理4[11]设u:(M,g)→(N,h)是从(M,g)到(N,h)的光滑映照,则有:
(divSF,H)(X)=-h(τF,H(u),du(X)),
(10)
其中X∈Γ(TM).
若u是带位势的弱F-调和映照,利用式(2)和式(10)可得:
(11)
其中X∈Γ0(TM).
由T=SF,H可知,对于任意X∈Γ0(TM)都有:
(12)
2 单调公式
设(M,g0)是有一个极点x0的完备黎曼流形.r(x)表示到极点x0的g0-距离函数,即
rx=distg0(x,x0).

设u:(Mm,g)→(N,h)是光滑映射,g=f2g0,0 (f2)存在常数C使得: -dFmax{2,λmax}≥C, 其中dF为[2,5]: 本文假定dF是有限的. h(N 由式(12)可得: (13) 直接计算可得: (14) (15) 和 (16) 由式(14),(15),(16)及(f1),(f2)可得: (17) 又由式(13)和式(17)可得: (18) 取一个正数ε并设φ是在[0,)于是: (19) (20) 则有 (21) 由式(18)和式(21)可得: 故 因此有 其中0<ρ1<ρ2.由于suppξρ⊆B((1+ε)ρ),故有: 令ε→0并注意到在B(ρ)上ξρ(r)=1,则可知定理结论成立.证毕. 定理2 设u:(M,f2g0)→(N,h)是带位势H的弱F-调和映照.若f满足(f1),(f2)且H≤0(或 H|u(M)≤0),则 (22) (23) 和 2dFmax{2,λmax})+ (24) 由式(22),(23),(24)以及(f1),(f2)可得: (25) 又由式(12),(21),(25)可得: 从而有 因此 其中0<ρ1<ρ2.由于suppξρ⊆B((1+ε)ρ)故有: 令ε→0并注意到ξρ(r)=1,则可知定理结论成立.证毕. 引理5[2,3,15]设(Mm,g)是具有极点x0的完备黎曼流形.Kr表示M的径向曲率. (1)若-α2≤Kr≤-β2,且α≥β>0,(m-1)β-2dFα>0,则 ((m-1)λmin+2-2dFmax{2,λmax})≥ ((m-1)λmin+2-2dFmax{2,λmax})≥ ((m-1)λmin+2-2dFmax{2,λmax})≥ 定理3 设(Mm,g)是有极点x0的m维完备流形.设M的径向曲率Kr满足下列三种情形之一: (1)若-α2≤Kr≤-β2,且α≥β>0,(m-1)β-2dFα>0; (2)若 若u:(M,g)→(N,h)是带位势的弱F-调和映照,H∈C(M)且则: 其中0<ρ1<ρ2. 注2 定理3由f=1时定理1的证明及引理5即可得证. 定理4 设(Mm,g)是有极点x0的m维完备流形.设M的径向曲率Kr满足定理3的条件.u:(M,g)→(N,h)是带位势的弱F-调和映照,H∈C(M)且H≤0(或H|u(M)≤0),则: 其中0<ρ1<ρ2.Λ由定理3给出. 特别地,若 则u为常数. 注3 定理4由f=1时定理2的证明及引理5即可得证.



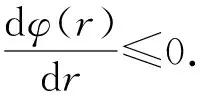
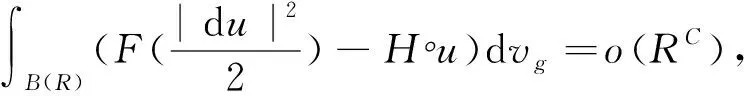







3 结论


