含二次隶属函数的模糊二次规划模型求解
卢树泉, 曹炳元
(广州大学 数学与信息科学学院, 广东 广州, 510006)
含二次隶属函数的模糊二次规划模型求解
卢树泉, 曹炳元
(广州大学 数学与信息科学学院, 广东 广州, 510006)
基于一种新定义的可调节二次隶属函数, 研究了一类带有模糊资源约束的模糊二次规划模型, 同时给出了两种相应的求解方法—扩展的Zimmermann算法和扩展的参数规划法。实例表明, 两类方法均有一定的合理性和有效性。
模糊二次规划; 二次隶属函数; 决策; 有效性
1 二次隶属函数的构造
在模糊集理论中, 模糊数是用隶属函数来表示的。针对线性隶属函数形式固定, 可调节性差的特点,构造具有二次形式的隶属函数。
1.1构造函数
设xL为模糊数x~的期望值, 它代表决策者最想要的结果;xU 是决策者认为最大可接受的上限数值。令具有二次形式的隶属函数为
根据隶属函数的性质: 当
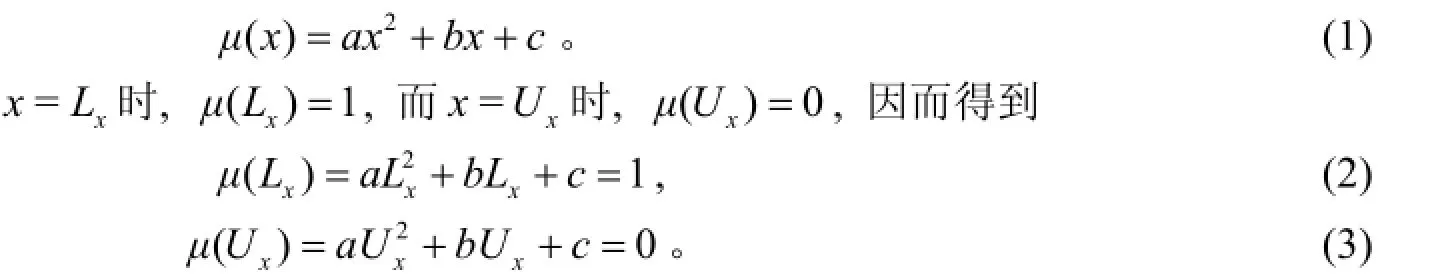
求解方程(2)、(3), 得出具含待定参数a的二次隶属函数
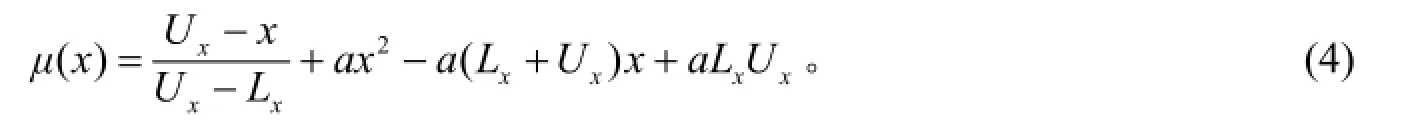
作为某个模糊数的隶属函数, 它还应该要满足在区间[Lx,Ux]严格单调下降的条件, 即或。
1.22种隶属函数的比较
对于二次隶属函数(4)而言: 当参数a取不同的值时, 尽管确定了二次函数的2点(Lx, 1)和(Ux, 0), 但是函数的弧度会有很大的区别, 所以在形式上它是可调节的。a取不同的值时, 某个可调节二次隶属函数的示意图如图1所示。
相对于线性隶属函数, 当确定了 2点(Lx, 1)和(Ux, 0)后, 这条直线就随之固定了, 其函数图像如图 1实线部分所示。可见, 线性隶属函数是二次隶属函数的特殊情况, 即取a=0时的情形。

图1 a取不同值时二次隶属函数示意图
2 带有二次隶属函数的模糊二次规划模型求解
模糊规划是普通规划的外延, 关于模糊线性规划的研究已逐步走向成熟, 其中最具有代表性的解法是Zimmermann算法[11]和参数规划法[12]。针对带有模糊资源约束的模糊二次规划问题, 提出了2种基于二次隶属函数的扩展Zimmermann算法和扩展参数规划法, 其本质是对线性方法的延伸。
2.1扩展Zimmermann算法
一般地, 带模糊资源约束的模糊二次规划问题具有如下的一般形式,
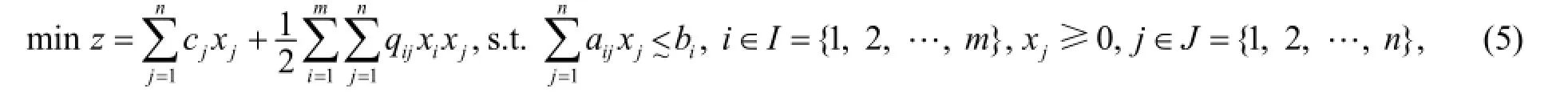
或改写成向量形式
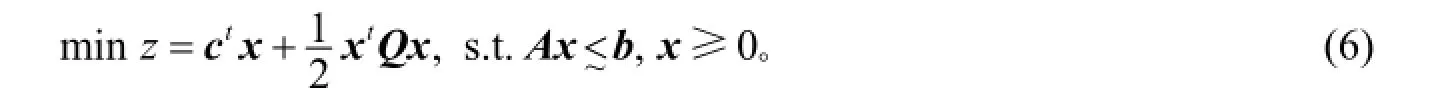
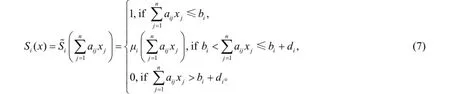
由于约束条件的模糊性必然导致目标函数的模糊性。为求模糊目标函数在模糊约束下的最优解, 可先将模糊目标函数化为约束条件。对应X中的一个模糊集M~, 取隶属函数为线性隶属函数
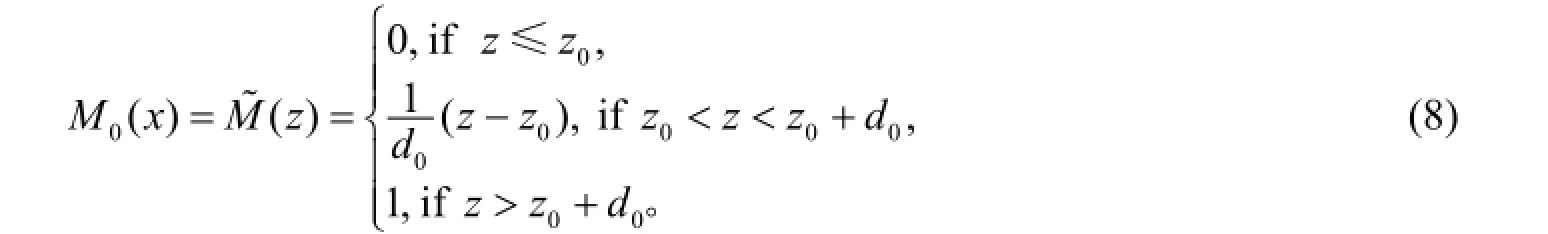
其中z0和z0+d0分别是严格遵守约束条件Ax≤b和约束条件放松至Ax≤b+d情况下目标函数的最优值。易见, S( x)和M( x)是相互矛盾的, 其中一方的增大会引起另一方的减少。同时兼顾模糊目标和模糊约束, Bellman和Zadeh[13]给出了模糊决策D~的概念: 模糊约束隶属函数和模糊目标隶属函数交点的最大值, 即

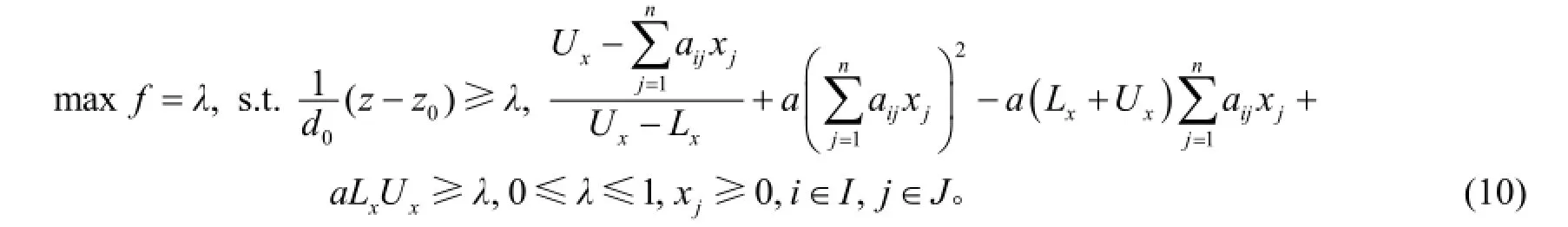
式(10)是一个带有约束条件的非线性规划问题, 可用罚函数等方法转化为无约束的非线性规划求解。扩展Zimmermann算法的主要思想是先将模糊约束集与模糊目标集分别表示成可调节的二次隶属函数和线性隶属函数的形式, 然后给出模糊决策的概念为两者隶属函数交点的最大值, 最终得出模糊最优解。
2.2扩展参数规划算法
所谓的参数规划, 是将式(5)所表达的模糊二次规划转化为带有待定参数θ的规划
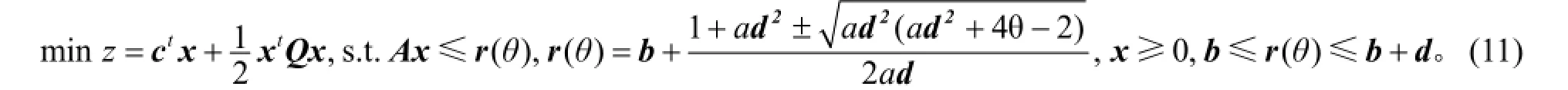
其中参数θ∈[0,1], r(θ)的取值可由二次隶属方程μ( x)=θ属于区间[b, b+d]的根来确定。显然, 当参数θ确定后, 式(11)便退化为一般形式的凸二次规划问题, 所以它的 Kuhn-Tucher必要条件同时也是充分条件。为求解规划(11), 构造拉格朗日函数[14]

这里μ是不等式约束的拉格朗日乘子向量。关于x∈Rn 求极小, 即令▽L( x,μ)=0, 将所得结果x=代到式(11)有
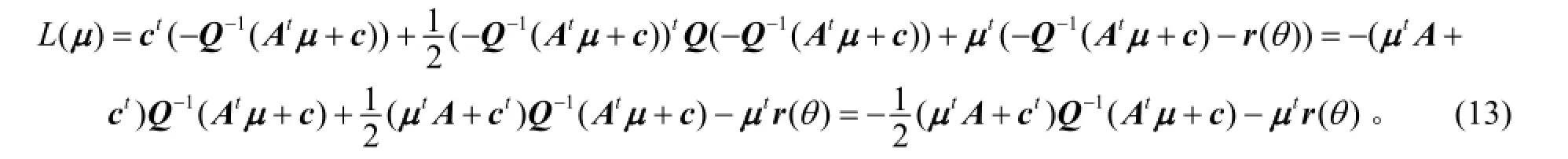
所以, 根据Lagrange对偶方法得出一个含参数的二次规划

扩展参数规划法的实质, 是通过约束条件的隶属函数定义的一个含有参数θ的规划, 这个参数表示对限制条件的偏离程度。一旦确定了该参数的取值, 相应地会有一个确定的二次规划与之对应。理论上, 由模糊集的表现定理, 整合所有参数在不同情况下的最优解便能得出结果。
3 数值例子
考虑带有模糊资源约束的模糊二次规划问题
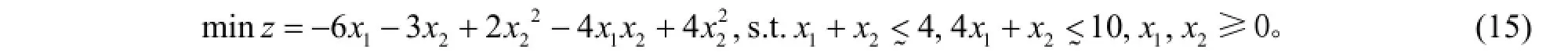
这里d=[2,5]是式(15)每个约束函数最大可接受的上限数值向量。因此, 当a=0.01时, 它们的二次隶属函数为:
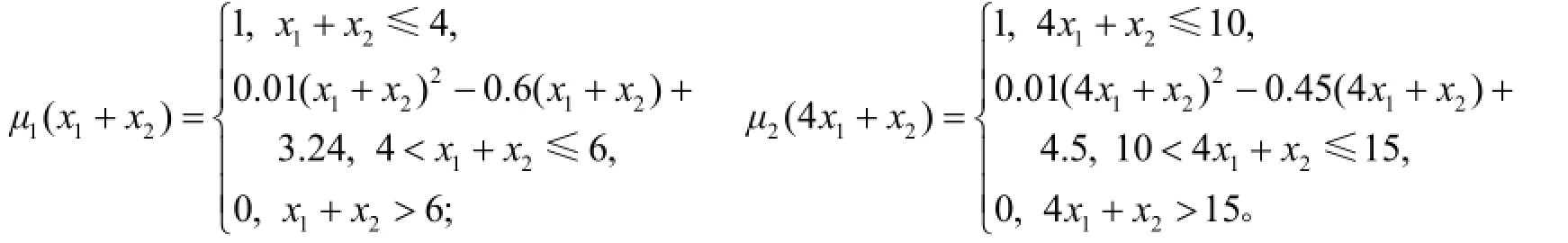
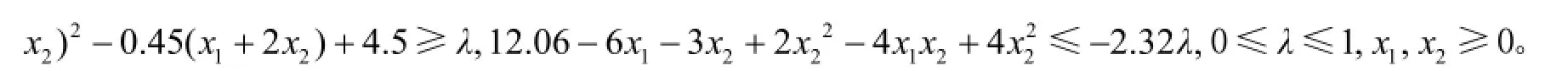
利用Lingo11软件求得λ=0.53, x1=2.61, x2=1.61, 其最优值为zmin=-13.31。与约束条件不添加缩伸时的最优值 z0=-12.06相比增加了 -1.25, 这是可行域增大的结果。
由式(11)、(15)可转化为一个含有参数θ的规划min z=或改写成Lagrange对偶形式
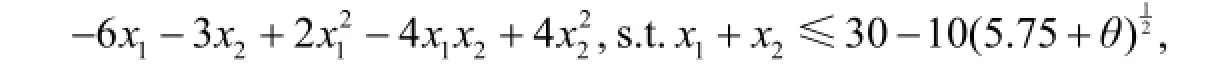
表 1呈现了θ取不同值时, 该参数规划的最优值情况。为了直观地说明扩展的Zimmermann算法和扩展的参数规划法之间的关系, 利用 Matlab软件分别作出扩展的Zimmermann算法下关于目标函数的隶属度直线和θ取不同值时扩展参数规划的最优值曲线, 如图2所示。由图2可知,2条线段交于点(-13.31, 0.53), 即是扩展Zimmermann的模糊最优解。
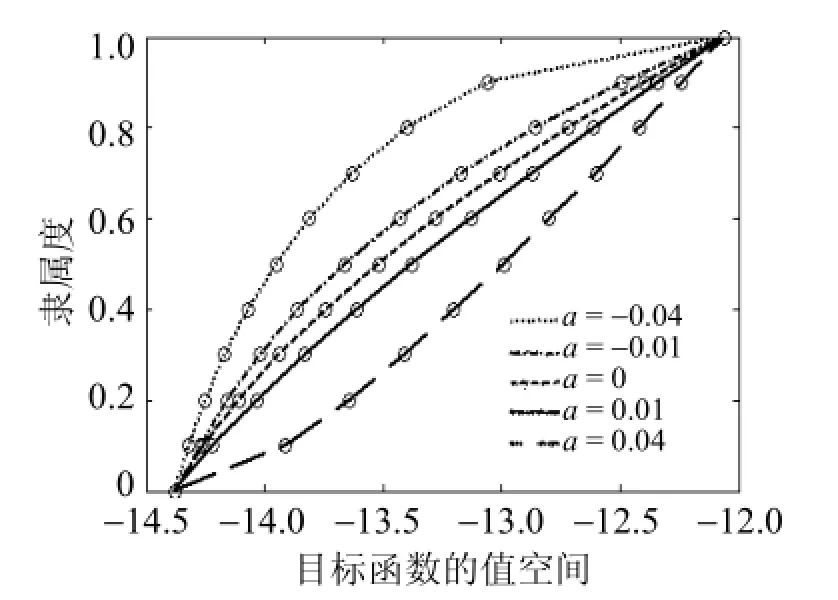
图3 a取不同值时扩展参数规划的最优值曲线
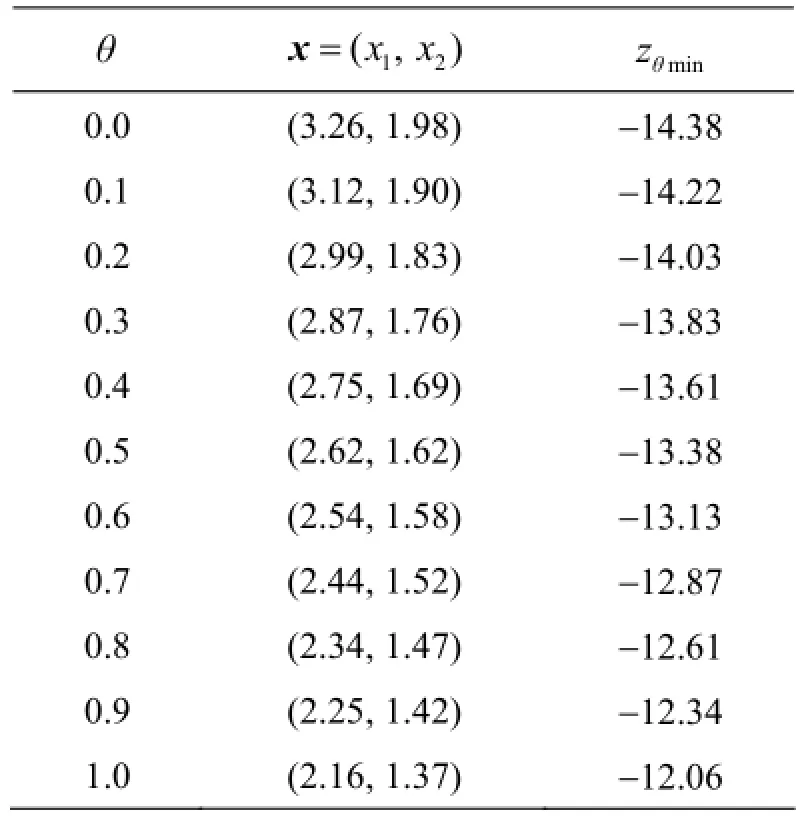
表1 θ取不同值时问题(14)的最优值情况
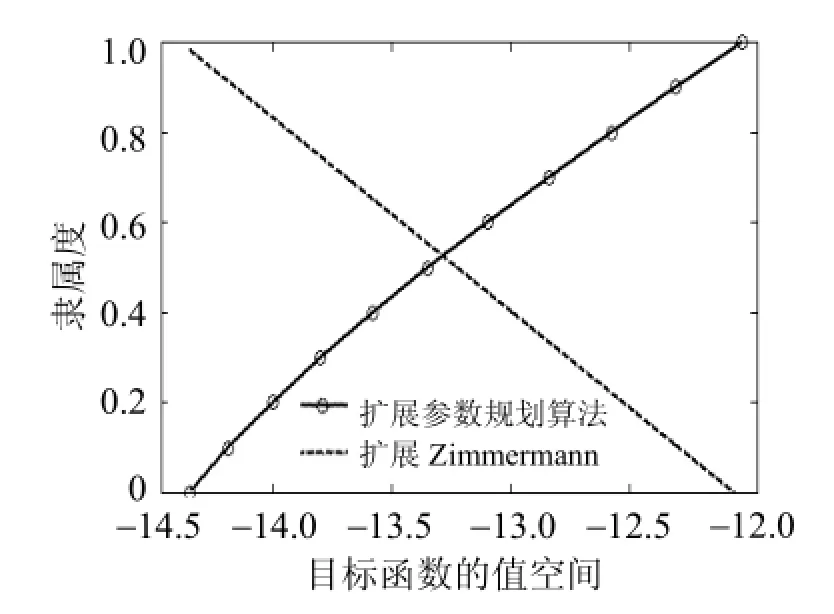
图2 2种方法的最优值曲线
另一方面, 隶属函数是决策者关于某个模糊概念的直观判断, 它的取值情况对最终的模糊判决有着非常大的影响。图3列出了可调节二次隶属函数的参数a取5组(a=0,a=±0.01和a=±0.04)不同值时, 该参数规划的最优值曲线。可以看出, 尽管其中有些参数只有细微的波动, 但是它们的最优值曲线还是相差较大的, 同时也说明了模糊最优解容易受到隶属函数的影响。
4 结论
本文针对一类带有模糊资源约束的模糊二次规划问题, 提出了一个具有二次形式的隶属函数, 它与传统的线性隶属函数相比更具有可调节性。基于这种二次隶属函数, 参照模糊线性规划的 Zimmermann算法和参数规划法, 平行地给出了2种扩展解法。实例表明, 扩展的Zimmermann算法和扩展的参数规划法, 对二次隶属函数的参数依赖程度高。尽管该参数发生细微的波动也可能导致最终模糊最优解产生较大的变化。事实上, 出现这种情况正是决策者所需要的, 因为待定参数的改变, 直接反映了一个模糊概念隶属程度的变化, 最终也必然影响模糊判决的好坏。因此, 选择一个合适的隶属函数是决策者做科学决策时最为关键的一步。
[1] 曹炳元. 应用模糊数学与系统[M]. 北京: 科学出版社, 2005: 117-130.
[2] Cruz C, Silva R, Verdegay J L. Extending and relating different approaches for solving fuzzy quadratic problems [J]. Fuzzy Optimization Decision Making, 2011, 10: 193-210.
[3] Silva R C, Verdegay J L, Yamkami A. Two-phase method to solve fuzzy quadratic programming problems [C]// IEEE International Conference Fuzzy Systems. London: Imperial College, 2007: 1-6.
[4] Silva R C, Yamakami A. A dual approach to solve fuzzy quadratic programming problems [C]// IEEE Fuzzy Information processing Society, 2011: 1-6.
[5] Liu S T. Quadratic programming with fuzzy parameters:a membership function approach [J]. Chaos Solitons and Fractals,2009, 40(1): 237-245.
[6] Liu S T. Solving quadratic programming with fuzzy parameters based on extension principle [C]// IEEE International Conference Fuzzy Systems. London: Imperial College, 2007: 1-5.
[7] Zhou X G, Cao B Y. Optimality conditions for fuzzy number quadratic programming with fuzzy coefficients [J]. Journal of Applied Mathematics, 2014(1): 1-8.
[8] Silva R C, Cruz C, Verdegay J L. Fuzzy costs in quadratic programming problems [J]. Fuzzy Optim Decis Making, 2013,12(3): 231-248.
[9] Silva R C, Cruz C, Verdegay J L. A survey of fuzzy convex programming [J]. Fuzzy Optimization, 2010, 254: 127-143.
[10] Murthy A S. Fuzzy programming with quadratic membership functions for Muti-objective transportation problem [J]. Pakistan Journal of Statistics & Operation Research, 2015, 5(2): 231-240.
[11] Zimmermann H J. Fuzzy mathematical programming [J]. Computers & Operations Research, 1983, 10(4): 291-298.
[12] Chanas S. The use of parametric programming in fuzzy linear programming in fuzzy linear programming [J]. Fuzzy Sets and Systems, 1983, 11: 243-251.
[13] Bellman R E, Zadeh L A. Decision-marking in fuzzy environment [J]. Management Science, 1970, 17(4): 141-164.
[14] 王宜举, 修乃华. 非线性最优化理论与方法[M]. 北京: 科学出版社, 2012: 165-167.
(责任编校: 刘晓霞)
Solution of fuzzy quadratic programming model with secondary membership function
Lu Shuquan, Cao Bingyuan
(School of Mathematics and Information Sciences, Guangzhou University, Guangzhou 510006, China)
Based on a new definition of secondary adjusted membership function, a class of quadratic programming model with quadratic membership function is studied, and then two corresponding solutions are presented, which extends Zimmmermann algorithm and parameter approach,respectively. The example shows that the methods have certain rationality and validity.
fuzzy quadratic programming; secondary membership function; decision making; effectiveness
O 221
1672-6146(2016)03-0001-05
10.3969/j.issn.1672-6146.2016.03.001
卢树泉, lusquan@163.com。
2016-01-23
在实际问题中, 非线性规划有着十分广泛的应用。无论是库存管理、投资组合、工程设计还是经济研究等领域都离不开特定形式的数学规划。但是, 到了真正的应用中, 有些参数可能并不是确定的, 而更多表现出来是模糊性。于是, 一种新的数学规划—模糊非线性规划[1]应运而生了。
目前, 关于模糊非线性规划问题的研究几乎都集中在模糊二次规划上。特别地, 针对具有模糊约束的模糊二次规划问题, Cruz[2]扩展了模糊线性规划中Zimmermann算法的一套理论, 并应用于求解模糊二次规划问题。基于参数规划法, Silva等[3-4]分别从原始问题和对偶问题2个角度对给定的α-水平下的普通二次规划进行求解, 通过整合这些α-最优解得到了模糊最优解。另外, 对于带有模糊系数的模糊二次规划问题, Liu等[5-6]应用Zadeh扩展原理将其转化为一个双层数学规划问题, 并利用非线性规划的有关知识进行了简化。Zhou等[7]则利用线性秩函数的方法来处理变量之间的这种模糊关系, 也给出了一个等价的二次规划问题, 其它的求解方法由文献[8-9]给出。受文献[10]的启发, 现有的许多文献都是用线性隶属函数来定义模糊约束集的, 这种类型的函数在形式上虽然简单, 但是有时并不符合决策者的意愿。为此, 本文先提出了一种具有二次形式的隶属函数。它与传统的线性隶属函数相比, 更具有可调节性。接着, 针对带有模糊资源约束的模糊二次规划问题, 分别采用扩展的Zimmermann算法和扩展的参数规划方法进行求解。最后, 用一个数值例子说明了它们的合理性和有效性。

