高中数学教学中学生学习的难点分析
宋兢利
高中学生在学习数学中存在的问题,可以归纳为不能理解抽象的数学知识的问题、数学知识系统不够完善的问题、不能准确地找到解题切入点的问题.
一、引导学生把抽象的问题变为具象的问题
在学习高中数学知识的时候,有些学生觉得高中数学问题的描述太抽象,他们不能理解这些数学问题.当这些学生反复阅读数学描述,依然不能理解数学问题时,便产生了学习挫折感,从而消极地对待学习.在高中数学教学中,教师要引导学生学会把抽象的数学问题变成直观的数学问题,以直观的角度来理解.
例如,在讲“集合”时,有位教师过去经常应用直接告诉学生抽象数学概念的方法,引导学生学习数学概念,后来很多学生表示教师讲的数学概念根本听不懂.后来这位数学教师便仔细地思考了教学方法,发现自己的教学方法不够直观,便在网上搜索了相关的多媒体视频,以后就用多媒体视频的方法引导学生学习集合的知识.当教师打开多媒体视频以后,多媒体便用动画的形式告诉学生什么是集合.它用一个圆圈表示一个集合,圈内的表示集合内的元素,圈外的表示集合外的元素.它又用到两集合运动,动画把交集的位置用彩色表示,说明这是两个集合共有的元素,两个集合交集越多,表示有共同的元素越多……多媒体直观动画的表现方法,让学生迅速地理解了什么是集合,以及与集合相关的数学概念.
二、引导学生用科学的思维理解具体的问题
在学习数学过程中,学生有时存在数学知识不系统、不能灵活应用数学知识的问题.在数学教学中,教师要引导学生一边学习一边整合数学系统,让学生以数学系统的角度理解数学知识,解决数学问题,提高学生的学习效果.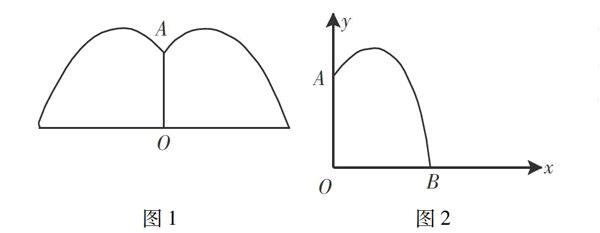
例如,在讲“微积分”时,有位教师以这样的方法引导学生学习函数概念知识:让学生了解圆的面积S与圆的半径r之间存在函数关系;锐角α与β互余,两者之间存在函数关系;气体的质量一定时,它的体积V与密度ρ之间存在函数关系.这几项知识是以前学生学习过的,他们能迅速地理解这三个函数关系式.当学生理解了这三个函数关系式以后,教师引导学生思考:这三个函数关系式有什么共同的特点呢?然后引导学生从集合、代数、几何这三个角度理解函数知识.这位数学教师给学生布置了一道经典的数学习题(略).这道数学习题,可以让学生以集合、代数、几何的角度来理解新的数学知识,使学生能够从系统的角度理解所有的知识,建立完善的数学知识系统.
在高中数学教学中,学生只有从数学知识系统的角度理解数学知识,以后遇到数学问题时,才能灵活运用数学知识.
三、引导学生用准确的切入,理解数学的问题
在解决数学问题的时候,有些学生空有一套数学知识系统,却找不到解题的切入点.为了引导学生找到正确的解题切入点,数学教师要引导学生在学习数学知识时学会找数学知识的特征.
例如,在讲“函数”时,有位教师提出问题:公园要造一个圆形喷水池,水池中央要造一个垂直的柱子OA,OA=1.25m,柱子的顶端A上要装一个喷头来喷水,水流柱在过OA的任一平面上抛物线路径如图1.为了让水流变得漂亮,要求让水流在距离OA 1m的地方达到最高的喷水高度.假设在没有其他因素的情况下,请设计水池的最小直径.
有些学生表示找不到这一题的解题切入点.这位教师引导学生观察图形.依题意可知,OA垂直于水面,且高度为OA=1.25m.现在设水池的半径为OB,那么可把这个问题转换为抛物线的问题,如图2,即已知抛物线AB,求直线OB的长度.将这个具象的生活问题,转化为抛物线问题,就是解决这个数学问题的切入点.在遇到数学问题时,教师要引导学生应用高度抽象的思想来观察数学描述,必要时应用数形结合、归纳类比等思想把数学问题变得抽象化,再抓住这个数学问题的抽象特征找到解决数学问题的切入点.
高中学生找不到数学问题的切入点,通常是由于学生不能用高度抽象的思想理解数学问题的缘故,数学教师要引导学生应用抽象的语言、抽象的符号、抽象的图象来理解数学问题,然后找到数学问题的特征.

