BIFURCATIONS AND NEW EXACT TRAVELLING WAVE SOLUTIONS OF THE COUPLED NONLINEAR SCHR¨ODINGER-KdV EQUATIONS∗

Heng Wang

（College of Global Change and Earth System Science（GCESS），Beijing Normal University，Beijing 100875，PR China）

Shuhua Zheng

（Investment and Development Department，Market and Investment Center，Yunnan Water Investment Co.，Limited，Yunnan 650106，PR China）



BIFURCATIONS AND NEW EXACT TRAVELLING WAVE SOLUTIONS OF THE COUPLED NONLINEAR SCHR¨ODINGER-KdV EQUATIONS∗

Heng Wang†

（College of Global Change and Earth System Science（GCESS），Beijing Normal University，Beijing 100875，PR China）

Shuhua Zheng

（Investment and Development Department，Market and Investment Center，Yunnan Water Investment Co.，Limited，Yunnan 650106，PR China）

Abstract

By using the method of dynamical system，the exact travelling wave solutions of the coupled nonlinear Schr¨odinger-KdV equations are studied.Based on this method，all phase portraits of the system in the parametric space are given.All possible bounded travelling wave solutions such as solitary wave solutions and periodic travelling wave solutions are obtained.With the aid of Maple software，the numerical simulations are conducted for solitary wave solutions and periodic travelling wave solutions to the coupled nonlinear Schr¨odinger-KdV equations.The results show that the presented findings improve the related previous conclusions.

dynamical system method；coupled nonlinear Schr¨odinger-KdV equations；solitary wave solution；periodic travelling wave solution；numerical simulation

2000 Mathematics Subject Classification 35Q51

1　Introduction

In recent years，the investigation of the exact travelling wave solutions to nonlinear wave equations plays an important role in nonlinear science，since the exact travelling wave solutions can provide much physical information and more insight of the physical and mathematical aspects of the problem and then lead to further applications.Several effective methods for obtaining exact travelling wave solutions of nonlinear wave equations，such as（G′/G）-expansion method［1］，the theta function method［2］，Darboux and Backlund transform［3］，tanh-coth method［4］，sine/cosinemethod［5］，Jacobi elliptic function expansion method［6］，the homogeneous balance method［7］，the symmetry method［8］，functional variable method［9］have been developed.Among them，the dynamical system method is one of these effective methods which has been applied to many nonlinear wave equations［10，11］.

In this paper，we consider the following coupled nonlinear Schr¨odinger-KdV equations［12］

where α，β are real parameters.u is a complex function and v is a real function. The study of coupled nonlinear Schr¨odinger-KdV equations has attracted extensive interest in physics and mathematics.Many numerical methods have been used to solve numerically the single nonlinear Schr¨odinger and the single KdV equation using finite element and finite difference methods［13-16］.Analytical solutions of the coupled nonlinear Schr¨odinger-KdV equations using different methods were given in［17-19］.Here，we shall use the dynamical system method to seek exact travelling wave solutions of（1.1）.

In order to find travelling wave solutions of（1.1），we assume that

where k，c，p and l are travelling wave parameters.

Substituting（1.2）into the first equation of（1.1），canceling eiηand separating the real and imaginary parts，we have

Obviously，from（1.3），we know that if ϕ′=0，then（1.1）has a trivial solution. Otherwise，（1.3）must be satisfied

Substituting（1.2）into the second equation of（1.1），and integraling once（integral constant is zero），we have

Therefore，（1.1）is reduced to

It is very difficult to solve this equations by some ordinary methods，so we consider the special transformation in subtle ways

Here，m is a constant to be determined later.Substituting（1.7）into（1.6），the system is changed into

Compared the coefficients of the second equation with those of the third equation of（1.8），we have

Under condition（1.9），system（1.8）is reduced to the following equation

which corresponds to the following two-dimensional Hamiltonian system

with the Hamiltonian

According to the Hamiltonian，we can get all kinds of phase portraits in the parametric space.Because the phase orbits defined the vector fields of system（1.12）determine all their travelling wave solutions of（1.1），we can investigate the bifurcations of phase portraits of system（1.12）to seek the travelling wave solutions of（1.1）.

The rest of this paper is built up as follows.In Section 2，we give all phase portraits of system（1.12）and discuss the bifurcations of phase portraits of system（1.12）.In Section 3，according to the dynamics of the phase orbits of system（1.12）given by Section 2，we obtain all possible bounded travelling wave solutions of（1.1）. Finally，a conclusion is given in Section 4.

2　Bifurcations of Phase Portraits of System（1.12）

In this section，we consider the phase portraits of（1.12）.Let right hand terms of system（1.12）be zeros，that is y=0，and Aψ+Bψ2=0，then the system（1.12）has two equilibrium pointsand O（0，0）.For the Hamiltonian H（ψ，y）=we write h0=H（0，0）=0With the change of the parameter group of A and Bthe system has different phase portraits for（1.12）as shown in Figs.1 and 2.

Figure 1：The bifurcations of phase portraits of（1.12）（A＞0，B＞0）.

Figure 2：The bifurcations of phase portraits of（1.12）（A＜0，B＞0）.

（1）When A＞0（＜0），O is a saddle point（center point）and S is a center（saddle point）.

（2）System（1.12）has a unique homoclinic orbit Γ which is asymptotic to the saddle and enclosing the center.There is a family of periodic orbits which are enclosing the center and filling up the interior of the homoclinic orbit Γ.

3　Exact Travelling Wave Solutions of（1.1）

In this section，we consider the bifurcations of the phase orbits of system（1.12）. Because only bounded travelling waves are meaningful to a physical model，we just pay more attention to the bounded solutions of（1.1）.In addition，because of B＞0，we just consider the travelling wave solutions of（1.1）when B＞0.According to equation（1.13），we haveSubstituting it intothat isBy using the Jacobian elliptic functions［20］，integratingwe can obtain the exact travelling wave solutions of（1.1）.（1）When A＞0，B＞0，there exists a smooth solitary solution which corresponds to a smooth homoclinic orbit Γ of（1.12）defined by H（ψ，y）=h0=0.We have the parametric representation

（2）When A＜0，B＞0，there exists a smooth solitary solution which corresponds to a smooth homoclinic orbit Γ of（1.12）defined by H（ψ，y）=h1.We have the parametric representation

（3）When A＞0（A＜0），B＞0，similarly，there exist periodic travelling wave solutions which correspond to the family of periodic orbits Γhof（1.12）defined by H（ψ，y）=h，h∈（h1，0）（h∈（0，h1））.We have the following parametric representation

where the parameters z1，z2，z3with z1＞z2＞z3are defined by y2=2h+Aψ2+

By using the above results and considering conditions（1.9），we obtain the exact travelling wave solutions of（1.1）as follows.

（1）When A＞0，B＞0，

（2）When A＜0，B＞0，

（3）When A＞0（A＜0），B＞0，

Based on the above results，by using the numerical simulation method，the 3D graphics of bounded solutions of（1.1）are shown in Figs.3-8（drawn by software Maple）.

Figure 3：The 3D graphics of|u1|（k=p= l=1，c=2，α=2，β=1，-5≤x≤5，0≤t≤0.5）.

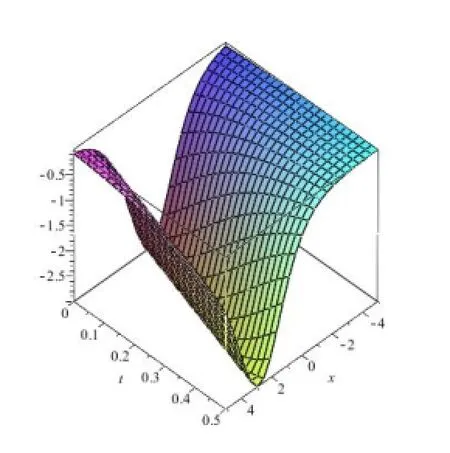
Figure 4：The 3D graphics of v1（k=p= l=1，c=2，α=2，β=1，-5≤x≤5，0≤t≤0.5）.

Figu√re 5：The 3D graphicsof√（k=1，p=1-，l=-1，c=2-，α=2，β= 1，-5≤x≤5，0≤t≤0.5）.

Figu√re 6：The 3D graphicso√f v2（k=1，p=1-，l=-1，c=2-，α=2，β= 1，-5≤x≤5，0≤t≤0.5）.

Figure 7：The 3D graphics of（k=p= l=1，c=2，h1=-，α=2，β=1，-5≤x≤5，0≤t≤5）.

Figure 8：The 3D graphics of v3（k=p= l=1，c=2，h1=-，α=2，β=1，-5≤x≤5，0≤t≤5）.

By using the approach of dynamical system，we obtain the travelling wave solutions of（1.1）.Among them，（3.4）and（3.5）are soliton solutions which are expressed by the hyperbolic functions.（3.6）is a periodic solution which is expressed by Jacobian elliptic function.Note that our solutions in this paper are different from the given ones in references［17-19］.

4　Conclusion

By using the method of dynamical system，the exact explicit travelling wave solutions of（1.1）are shown which have periodic wave solutions and solitary wave solutions.Of course，the dynamical system method is not only able to solve the coupled nonlinear Schr¨odinger-KdV equations，it can also be applied to some other nonlinear equations.

Furthermore，if without the condition that B＞0，system（1.12）has another case.If A＞0（A＜0），B ＜0，there exist periodic travelling wave solutions corresponding to the family of periodic orbits Γhof（1.12）defined by H（ψ，y）=h，h∈（h1，0）（h∈（0，h1））.We have the following parametric representation

where the parameters z1，z2，z3with z1＞z2＞z3are defined by y2=2h+Aψ2+Then we obtain additional travelling wave solutions of（1.1）as follows：

References

［1］M.Wang，X.Li，J.Zhang，The（G′/G）-expansion method and traveling wave solutions of nonlinear evolution equations in mathematical physics，Phys.Lett.A，372（2008），417-423.

［2］K.W.Chow，A class of exact periodic solutions of nonlinear envelope equation，J.Math. Phys.，36（1995），4125-4137.

［3］V.B.Matveev，M.A.Salle，Darboux Transformation and Solitons，Springer，Berlin，1991.

［4］A.M.Wazwaz，The tanh-coth method for solitons and kink solutions for nonlinear parabolic equations，Appl.Math.Comput.，188（2007），1467-1475.

［5］C.T.Yan，A simple transformation for nonlinear waves，Phys.Lett.A，224（1996），77-84.

［6］G.T.Liu，T.Y.Fan，New applications of developed Jacobi elliptic function expansion methods，Phys.Lett.A，345（2005），161-166.

［7］M.L.Wang，Solitary wave solutions for variant Boussinesq equations，Phys.Lett.A，199（1995），169-172.

［8］C.M.Khalique，A.Biswas，A Lie symmetry approach to nonlinear Schr¨odinger's equation with non-Kerr law nonlinearity，Commun.Nonlinear Sci.Numer.Simul.，14：12（2009），4033-4040.

［9］M.Mirzazadeh，M.Eslami，Exact solutions for nonlinear variants of Kadomtsev-Petviashvili（n，n）equation using functional variable method，Pramana J.Phys.，81：6（2013），911-924.

［10］Jibin Li，Singular Nonlinear Travelling Wave Equations：Bifurcations and Exact Solutions，Beijing：Science Press，2013.

［11］Jibin Li，Hui-hui Dai，On the Study of Singular Nonlinear Travelling Wave Equations：Dynamical System Approach，Beijing：Science Press，2007.

［12］T.Yoshinaga，M.Wakamiya and T.Kakutni，Recurrence and chaotic behavior resulting from nonlinear interaction between long and short waves，Phys.Fluids A，3：1（1991），83-89.

［13］I.Christie，D.F.Griffiths，A.R.Mitchell，and J.M.Sanz-Serna，Product approximation for nonlinear problems in the finite element method，IMA Journal of Numerical Analysis，1：3（1981），253-266.

［14］J.M.Sanz-Serna and I.Christie，Petrov-Galerkin methods for nonlinear dispersive waves，Journal of Computational Physics，39：1（1981），94-102.

［15］S.W.Schoombie，Spline Petrov-Galerkin methods for the numerical solution of the Korteweg-de Vries equation，IMA Journal of Numerical Analysis，2：1（1982），95-109.

［16］H.Wang，Numerical studies on the split-step finite difference method for nonlinear Schr¨odinger equations，Applied Mathematics and Computation，170：1（2005），17-35.

［17］R.Abardeh，M.Ramezanpour，A.Doosthoseini，and E.Rezaie，New method for solving coupled Schr¨odinger-KdV equation，Applied Mathematical Sciences，7：86（2013），4273-4280.

［18］D.Kaya and S.M.El-Sayed，On the solution of the coupled Schr odinger-KdV equation by the decomposition method，Physics Letters A，313：1-2（2003），82-88.

［19］M.Labidi，G.Ebadi，E.Zerrad，and A.Biswas，Analytical and numerical solutions of the Schr¨odinger-KdV equation，PramanaJournal of Physics，78：1（2012），59-90.

［20］P.F.Byrd，M.D.Fridman，Handbook of Elliptic Integrals for Engineers and Scientists，Springer，Berlin，1971.

（edited by Mengxin He）

∗Manuscript received May 6，2015；Revised June 11，2016†Corresponding author.E-mail：1187411801@qq.com