例析以立体几何为载体的空间最值问题的求解策略

2016-12-16 08:11侯军苗会

侯军● 苗会●

云南省红河州石屏高级中学 (662200) 中央民族大学附中海南陵水分校(572400)

侯军● 苗会●

云南省红河州石屏高级中学 (662200) 中央民族大学附中海南陵水分校(572400)

在近几年的高考题和高三模拟题中经常出现一类以立体图形为载体的空间最值问题,这类问题对学生的识图、用图能力以及对立体图形的空间想象力要求较高，有助于考查学生的探究能力和思维的创造性.在教学中，我们发现同学们面对此类问题时普遍不知如何下手，故本文以此为背景，介绍几种求解立体几何最值问题的常用策略.

策略一直观感知，考虑特殊位置

例1 (2016浙江卷理科第14题)如图1，在△ABC中，AB=BC=2,∠ABC=120°.若平面ABC外的点P和线段AC上的点D，满足PD=DA,PB=BA,则四面体PBCD的体积的最大值是____.

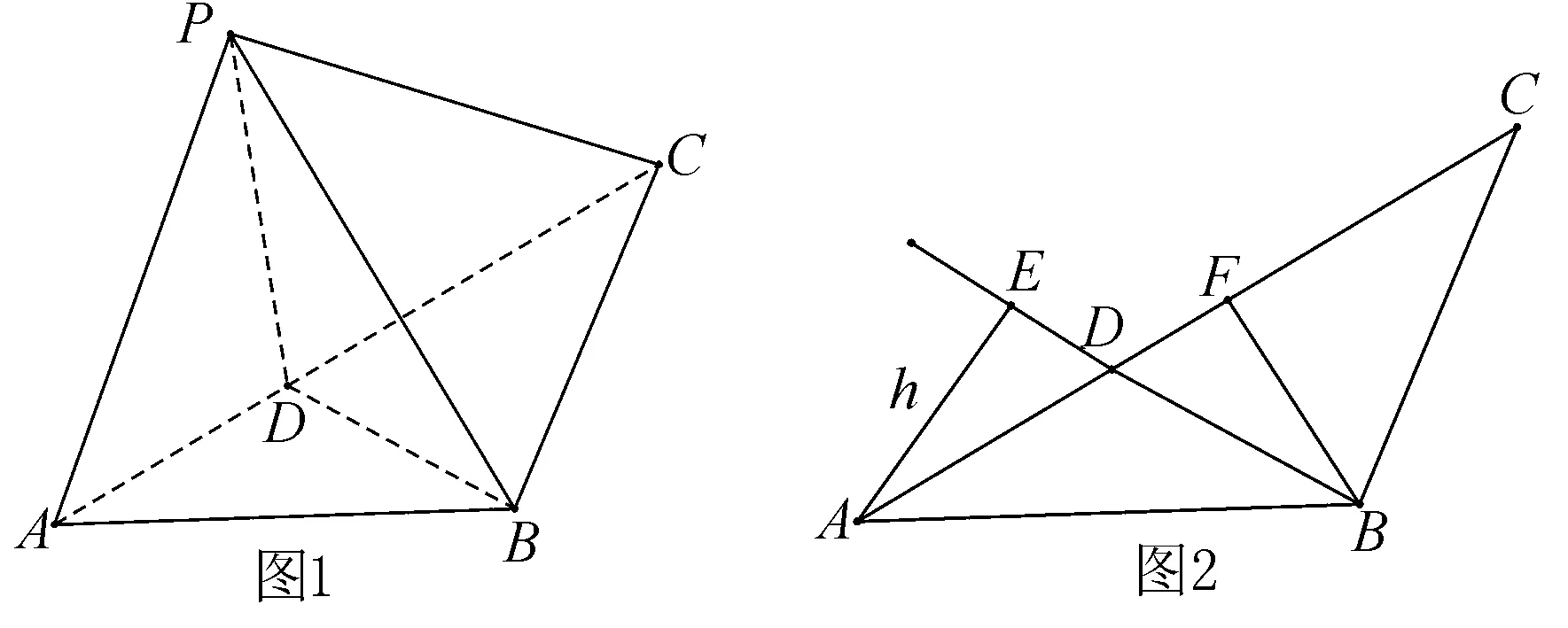
分析因为PD=DA,PB=BA,则本题可转化为△ABC沿着BD翻转过程中,何时三棱锥P-BCD的体积取得最大值. 通过几何直观感知可知，当平面PBD⊥平面BCD时，体积取得最大值.

点评本题关键在于对PD=DA,PB=BA这一条件的巧妙解读，使问题转化为翻转问题这一我们熟悉的题型.

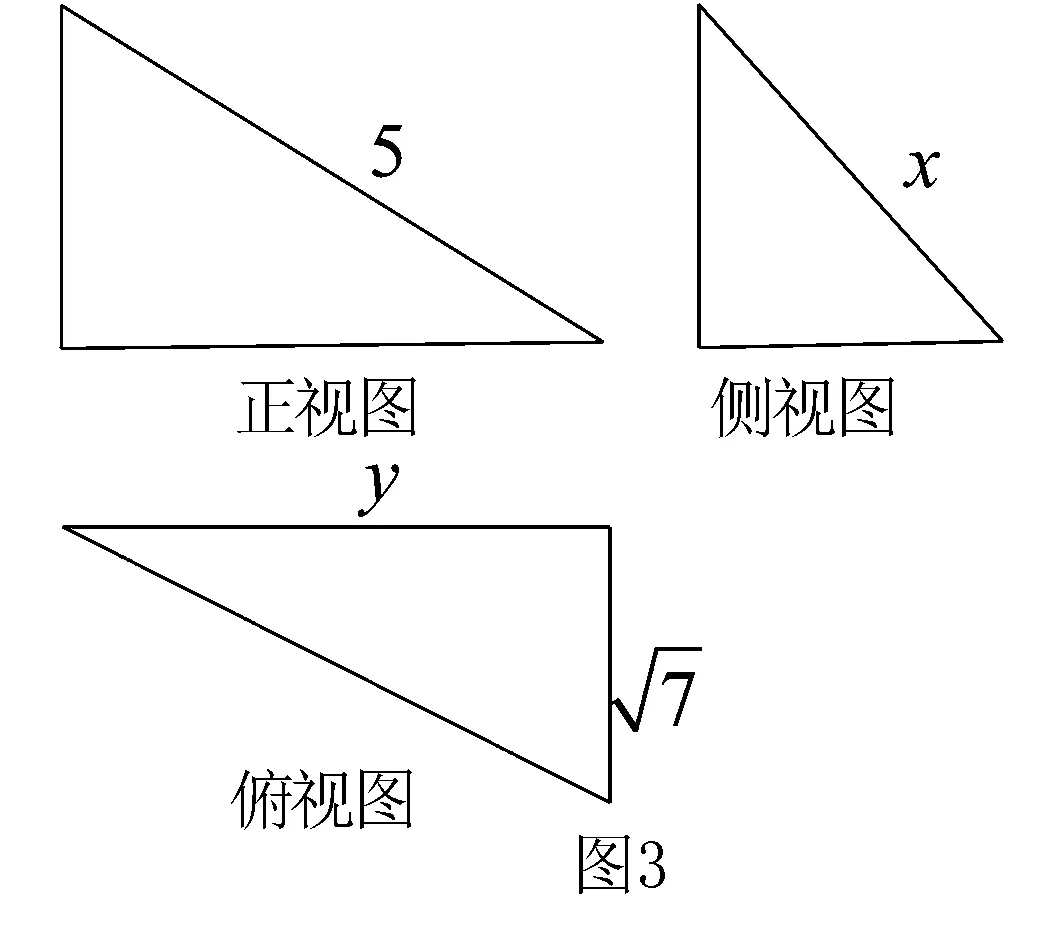
例2 某几何体的三视图如图3所示,当xy最大时,该几何体的体积为____.

分析由三视图为三个三角形可知几何体为三棱锥，考虑到“正、侧、俯视图长对正，正、侧视图高平齐，俯、侧视图宽相等”的特点可以找出三棱锥的关键数据，进而利用均值不等式构造不等关系求最值.

解该几何体的直观图如图4所示：

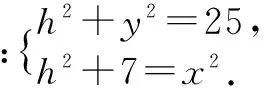
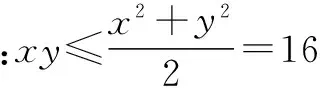
点评同学们不难画出该三视图所对应的直观图，本题的“卡点”在于很多同学不知道如何合理地构造不等关系，事实上，在立体几何中搭建不等关系时，a2+b2≥2ab这一结构的基本不等式使用频率更高，这主要源于它与勾股定理a2+b2=c2这一代数结构的知识联结.

例3 已知正六棱柱的12个顶点都在一个半径为3的球面上，当正六棱柱的体积最大时，其高为 ( ).

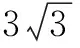
分析正六边形可以划分为6个正三角形，这也是求正六边形底面面积的常用思路.考虑到正六棱柱的对称性，故其外接球的球心必为上下底面中心连线的中点，不妨以高为自变量建立关于体积的函数，将问题转化为求函数的最大值问题.

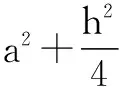
点评以立体几何为依托建立函数关系时，出现了我们熟悉的三次函数，对于绝大多数同学而言，通过求导的方法来求函数的最大值自然变得亲切、可爱，易于联想.

例4 (2012年上海卷理科第14题)如图6所示,AD与BC是四面体ABCD中互相垂直的棱,BC=2,若AD=2c,且AB+BD=AC+CD=2a,其中a,c为常数,则四面体ABCD的体积的最大值是____．

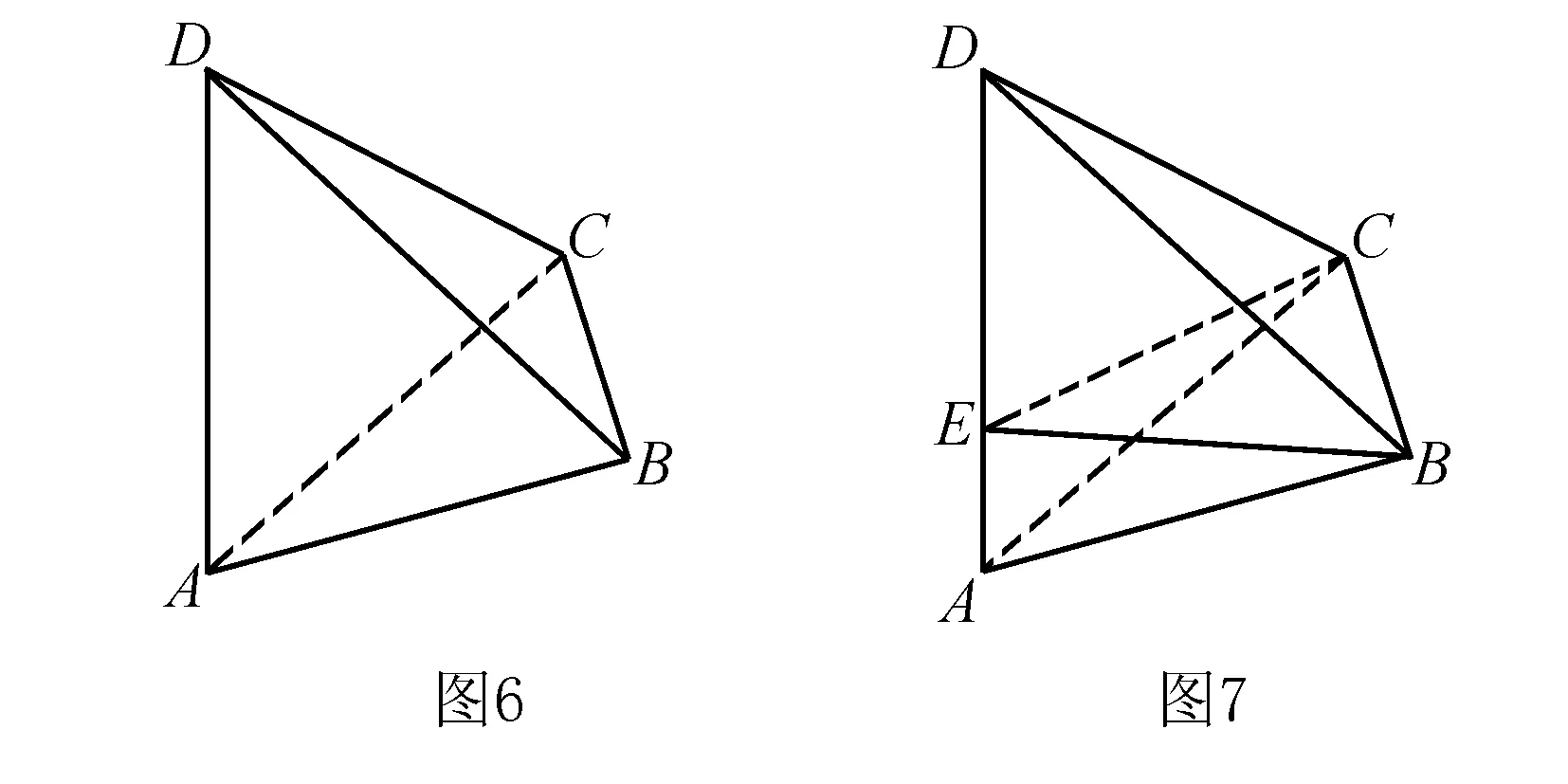
分析 “AD与BC是四面体ABCD中互相垂直的棱”是本题的重要切入点，不妨过点B作该四面体的一个垂面BCE，将四面体的体积进行“切割”.

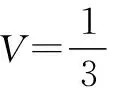
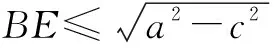
点评本题初看毫无头绪，将四面体“切割”后，运用椭圆的定义将立体几何问题巧妙的转化为解析几何问题处理，让问题变得柳暗花明，可见同学们在解题时要充分联想，敢于尝试.

例6 如图8所示，已知正四面体ABCD的棱长为1,M为BC的中点,P在线段DM上,则(AP+BP)2的最小值为____.

分析只需求AP+BP这一线段和的最小值，故我们不妨将立体图形展开为平面图形再利用平面内两点间距离最短这一性质进行求解.

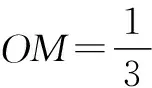
点评将立体图形沿某条棱展开成平面图形是求此类线段和最值问题的通性通法，其特点是通过展开平面使两条线段在同一个平面内.本题不仅运用了这一方法，更在此基础上应用余弦定理，考查了学生对已学知识的有效迁移能力.

G632

1008-0333(2016)28-0009-02