繁与简是一念间的事
——一道试题的解法探究与反思收获

束仁武 (邮编：611731) 周纯舫 (邮编：230001)

安徽省合肥市庐江第四中学 安徽省合肥市庐江第二中学

繁与简是一念间的事
——一道试题的解法探究与反思收获

束仁武 (邮编：611731) 周纯舫 (邮编：230001)

安徽省合肥市庐江第四中学 安徽省合肥市庐江第二中学

问题是数学的心脏.在教学课余时，同学们总找一些感兴趣的问题跟我们交流.面对这种情况，我们虽然深知要有“一桶水”，但在没有参考答案的情况下，要一眼就能寻找到最优化的解题方案，我们还需不断研修.

我们对学生提问的问题时，不能“避难就易”，会的就解答，不会的就找借口，三两次下去，同学们就会对教师的解题水平产生怀疑，影响教师在学生心目中的可信度.所以，在同学们提出问题时，我们力求迅速指明解题思路，及时给出满意解答，但由于时间仓促，老师有时候也会犯傻.这正如罗增儒教授指出：解题笨拙与解题智慧相对，有时真是用了多余的知识，走了多余的思维回路，人为地拉长了解题的长度，表现为解题笨拙.当出现解题笨拙时，要通过反思，找回解题智慧.我们列举一个发生在身边的案例，进行剖析，体会“简繁之间只是一念之差”.

1 问题及解法探究

我们在上《几何证明选讲》专题后，就遇到这样的一幕：同学A兴冲冲拿着一道平面几何题来问我们.

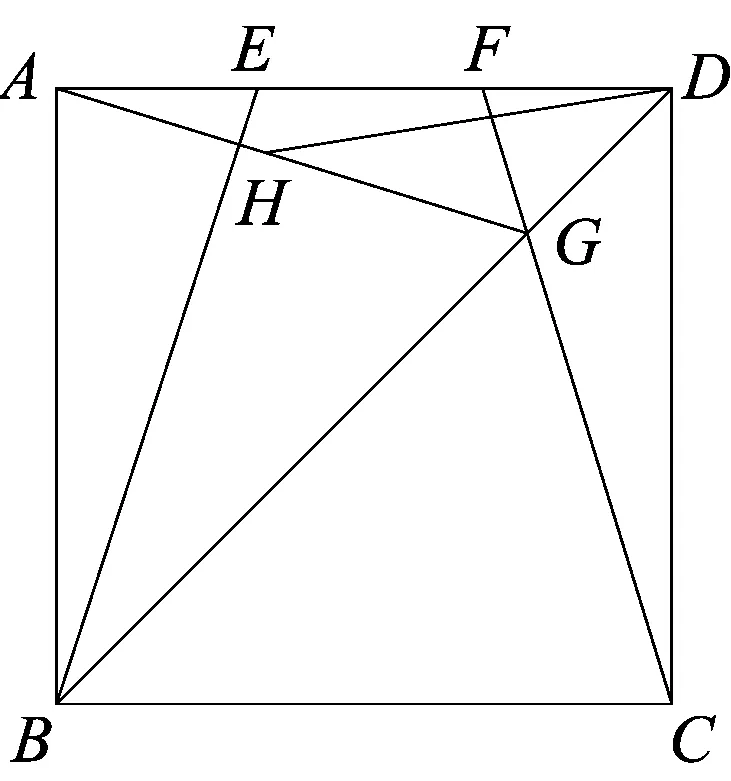
图1

题目 如图1,在正方形ABCD中，AB=4，E、F是边AD上两动点，AE=DF=a，连接CF交BD于G，连接AG交AE于H，求DH长度的最小值是多少？

乍看这题，点E、F在AD上运动，连接CF交BD可以确定动点G，连接AG交AE可以确定动点H.要求DH的最小值？可以依据解析思想把几何问题转化为代数问题.求出H点的轨迹方程，弄清H点的轨迹，从而确定何时DH最小，并求出最小值.

图2

图3

于是，我们就采取建立直角坐标系，通过建立直线方程来解决.

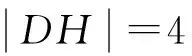
(2) 当E不与A和D重合时，设：

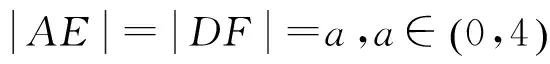
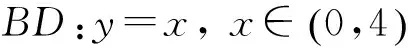
①

②

联立①，②方程：

所以G的坐标为

③

④

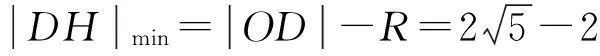
解题后我们继续思考：求DH的最小值，终归是求最值问题，所以我自然的联想到函数的基本性质——最值.求DH的最小值，不就是要建立变量DH与变量AE(或AF=a)的函数关系式，再通过确定的函数关系式，求出函数最小值.从而我们得到以下两种解答过程.

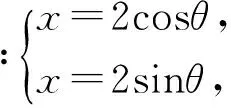
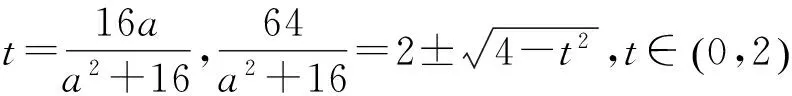
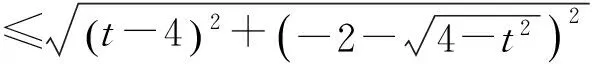
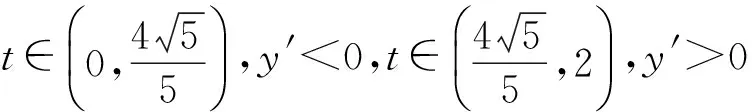
通过以上三种方法，我们发现第三种方法比前面两种方法更繁琐，这种定量分析的解析法的确繁赘，难以置信.于是，我们就思考，有没有更简便的方法呢？难道这道题变量a的变化对线段DH的变化没有更直观的几何解释吗？我们能否用几何的方法来作定性考查呢？

图4

解法4 如图4，在正方形ABCD中，BD为对角线，

根据对称性可知：∠2=∠3，

在△ABE和△DCF中，AB=CD，∠BAE=∠CDF，AE=DF，∴Rt△ABE≌Rt△DCF，∠1=∠2，∠3=∠1.

而∠BAH+∠3=90°，∠BAH+∠1=90°，则BE⊥AG，由此可知：不论E、F两动点在AD上如何运动，∠AHB=90°的值不变.

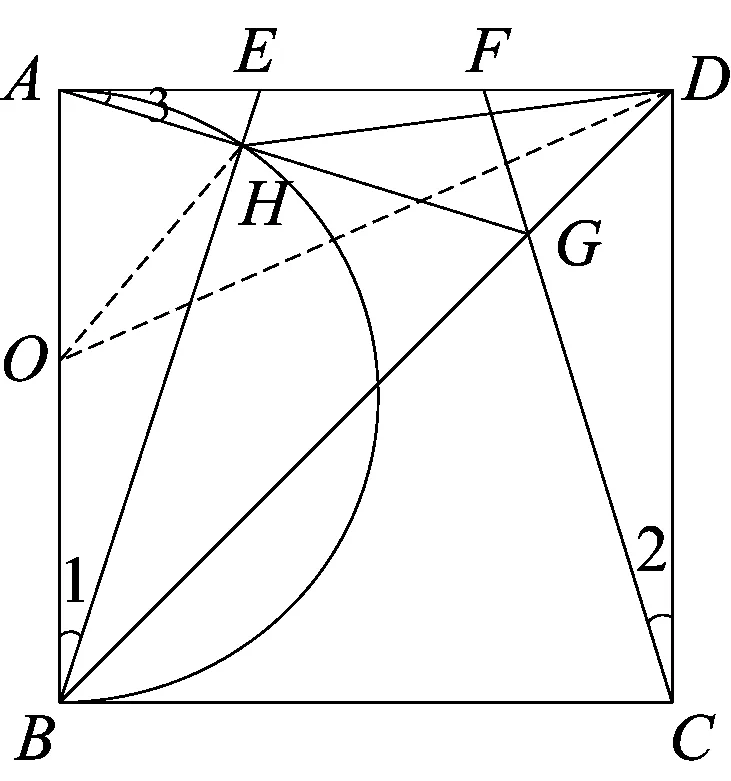
图5

根据三角形的三边关系，OH+DH>OD，当O、D、H三点共线时，DH的长度最小.

2 反思收获

下面，我们再深入反思这道题的价值，还是收获颇丰.

反思收获1 如果点E、F两点在AD所在的直线上运动，其它条件不变，那么点H形成的轨迹是什么？既然有最小值，那么点D到H之间的距离有没有最大值呢？最大距离是多少？

剖析 当E、F继续在AD所在的直线上运动，我们借助几何画板演示，发现H点的轨迹还会变成一个以AB为直径的半圆(如图5).

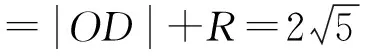
反思收获2 我们从答案来看，这个数值是巧合呢？还是另有缘由？如果将DH的长度与正方形边长AD相比是什么呢？

在直角三角形△OAD中，∠A=90°，且AD=2AO，就可以构造黄金分割点.这不真是我们探究发现又一种作黄金分割的方法吗？虽然方法还雏嫩，但不能不说是一种好想法.

反思收获3 如果把正方形改为正五边形呢，其它条件不变，是否有类似的结论呢？如果我们把正方形改为正六边形呢？其它条件不变，是否有类似的结论呢？……，如果我们把正方形改为正n边形呢？其它条件不变，是否有类似的结论呢？

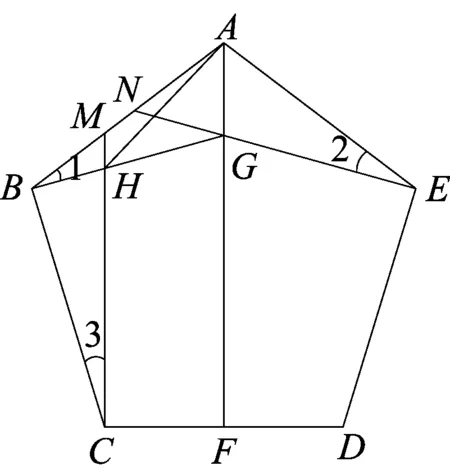
图6

回答是肯定.对于正五边形来说，如图6，已知正五边形ABCDE，AF是其中一条对称轴，点M、N为边AB上两动点，且AN=BM，连接EN交AF于G点，连接BG交CM于H，则∠BHC为定值.其定值为；点H的轨迹在以BC为劣弧所含的圆周角为72°的圆弧上.

图7

如图7，已知正六边形ABCDEF，点M、N为边AB上两动点，且AN=BM，连接FN交AD于G点，连接BG交CM于H，则∠BHC为定值，其定值为=60°；点H的轨迹在以BC为劣弧所含的圆周角为60°的弧上.

一般地，有类似性质，这里不再赘述.

反思收获4 这题探究到此，我们进一步发现，它可以派生出安徽省2016年数学中考题第10题：

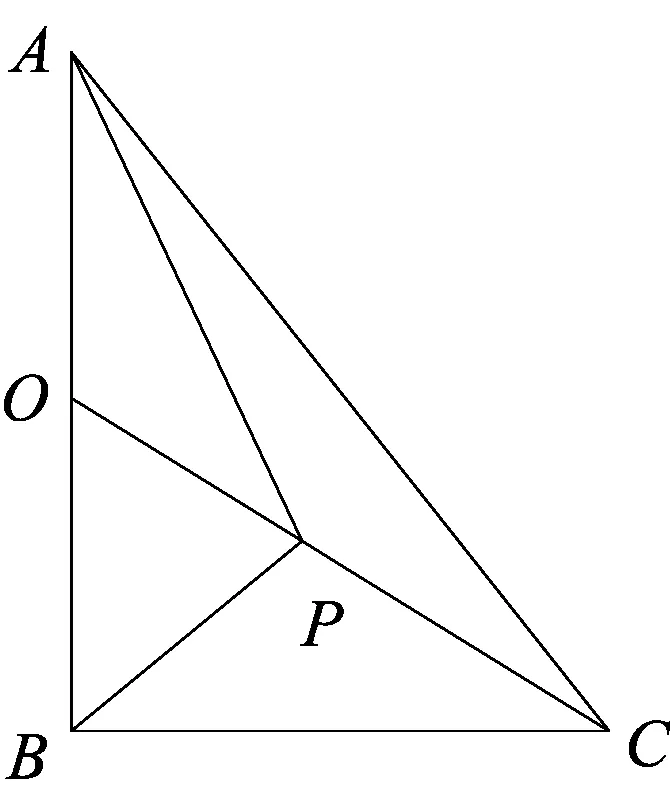
图8

如图8，Rt△ABC中，AB⊥BC，AB=6，BC=4，P是ABC内部的一个动点，且满足∠PAB=∠PBC，则线段CP长的最小值为( )

答案是B.

理由如下：∵∠PAB=∠PBC，AB⊥BC，

∴∠ABP+∠PBC=90°，

∴∠PAB+∠ABP=90°，∴∠APB=90°，

∴点P在以AB为直径的⊙O上.

故当OP=2时，CP最小值为3.

3 自我成长

3.1 解题笨拙与智慧

对于以上四种解题方法分析可见，开始时，我们在学习《平面几何选讲》时，学生冷不丁地提出问题，我们根据学生当前的知识存储，联想到用解析法建立方程求交点，解决动点距离问题.其实，这是在选择解题方法上的盲从，没有进行深入考虑，没有进行“解题智慧”的挖掘，而是被题目中提供的表面现象所迷惑，误以为建立函数关系来求最小值，比较简单，其实增加了“解题长度”，运用了多余的知识，所以，走到“解题笨拙”的一面.为了避免少走弯路，减少解题中长度，绕开解题笨拙，还是要在审题时多思考，化繁为简，才会应运而生地出现“绝处逢生”的美巧想法，解题后的几点反思，真是点滴心血筑成的.

3.2 专业成长

教师在专业成长的过程中，为什么要不断地提高自我专业水平呢？只有通过研修，才能不断提升自我.通过解析法、参数法和函数法求解，会发现直线AG、BE位置关系，确定动点H的所在方程，判定动点H是以AB为直径的半圆轨迹，而要求DH的最短距离，就是求点到圆上最短距离.进而为解法4提供强有力的支撑，解法4是纯平面几何的证法，通过反思联想，把这道题与一道中考题成功对接，缩短了知识间的距离.这道题解答探究过程就是一个成功的案例.

这种方法探究成功，进一步说明，教师的专业成长要不断地研修，只有站得高，才能看得远.用高层次的知识居高临下指导教学，在指导教学实践过程中，不断储蓄知识，积蓄能量，拓展解题思路.

当我们重新审视这道题的探究历程时，却有“众里寻它千百度,蓦然回首，那人却在灯火阑珊去”的感觉！其实，这道题的本质就是求点到圆上最短距离问题，真是繁与简是一念间的事.

1 罗增儒. 数学解题学引论[M].西安：陕西师范大学出版社,2001

2017-01-18)