基于FLUENT CFD的椭圆形水下滑翔器伯努利方程验证
欧启彬, 黄 技, 欧启明
(1.广东海洋大学 海洋工程学院, 广东 湛江 524088; 2.仲恺农业工程学院 计算科学学院, 广东 广州 510550)
基于FLUENT CFD的椭圆形水下滑翔器伯努利方程验证
欧启彬1, 黄 技1, 欧启明2
(1.广东海洋大学 海洋工程学院, 广东 湛江 524088; 2.仲恺农业工程学院 计算科学学院, 广东 广州 510550)
利用软件FLUENT CFD对某椭圆形滑翔器不同来流速度进行数值模拟,并且运用流体力学中的伯努利方程对椭圆形浮标周围物理场进行验证。结果表明,椭圆形水下滑翔器周围流场中,在同一条流线上各点的单位重量流体所具有的总机械能近似相等,即一条流线上不同点的动能、压力能、位置势能之和是一个定值,并且误差不超过3%,从而验证了伯努利方程在全流场流线的任何一点上均成立。通过数值模拟验证伯努利方程,可知椭圆形水下滑翔器满足一般的水动力性能要求。
伯努利方程;FLUENT;数值模拟;椭圆形水下滑翔器
0 引言
伯努利方程是流体动力学常用的基本方程之一[3],是指在流体定常流动的前提下,不考虑黏性的流动中,流线上不同点的动能、压力能、位置势能之和保持不变。伯努利方程[3]是能量守恒定律在理想流体定常流动中的运用,其实质是指机械能守恒定律在水流运动中的运用。1738年瑞士数学家丹尼尔·伯努利(Daniel Bernoulli)首次提出了伯努利原理,之后科学家将伯努利积分、伯努利定理统称为伯努利方程。本文从计算流体力学(Computational Fluid Dynamic, CFD)的角度出发,利用FLUENT软件对伯努利方程进行验证,各点的动能、压力能、位置势能之和稳定在常数范围内,且误差不超过3%,从而验证伯努利方程。通过FLUENT软件的数值模拟,证明发明的椭圆形水下滑翔器满足一般的水动力性能要求,为进一步分析其水动力性能打下坚实基础。
1 伯努利方程原理
1.1 伯努方程推导
根据质点的随体函数公式
(1)
以及矢量场论的基本运算公式
(2)
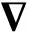
(3)
在流体力学中,把这个方程称为兰姆-葛罗米柯(Lamb-Gromicco)型运动方程,其特点就是将打涡量ω引入方程,突出流场的有旋性,同时,在一定的附加条件下,这个方程就有可能变为微分方程,使之便于积分计算,本文的伯努利方程推导就是从这个方程引出得到的。
1.2 定常流动中的伯努利方程
1.2.1 定常流动
对式(3)进一步简化得
(4)
式(4)可以沿一条直线积分,由于在定常流场中副流线形状和位置是不随时间变化的,因此可任取一条流线ψ,设此流线上微元弧长矢量为ds,用ds点乘式(3)两边,即有
(5)
从而得到:
(6)
1.2.2 定常流动的伯努利方程
对式(6)积分后得
(7)
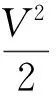
2 工况设计和数值模拟
2.1 计算模型
图1为某椭圆形水下滑翔器的模型,图2为测点编号。流场及模型网格如图3和图4所示。

图1 某椭圆形水下滑翔器模型

图2 测点编号
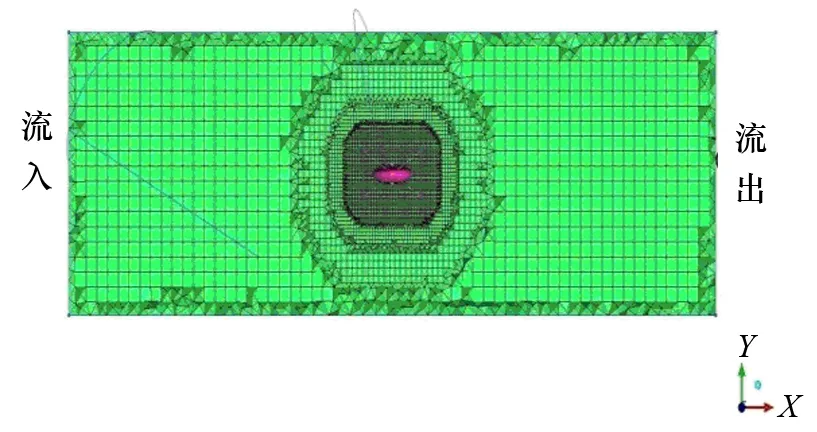
图3 核心局域网格
2.2 试验工况设计
2.2.1 定常工况
表1为试验定常工况各参数的取值。
2.2.2 定常工况云图
图5为ESV0.1~ESV2.0定常流动速度云图。图6为ESV0.1~ESV2.0定常流动压力云图。图7为ESV0.1~ESV2.0定常流动速度矢量图。

表1 试验定常工况
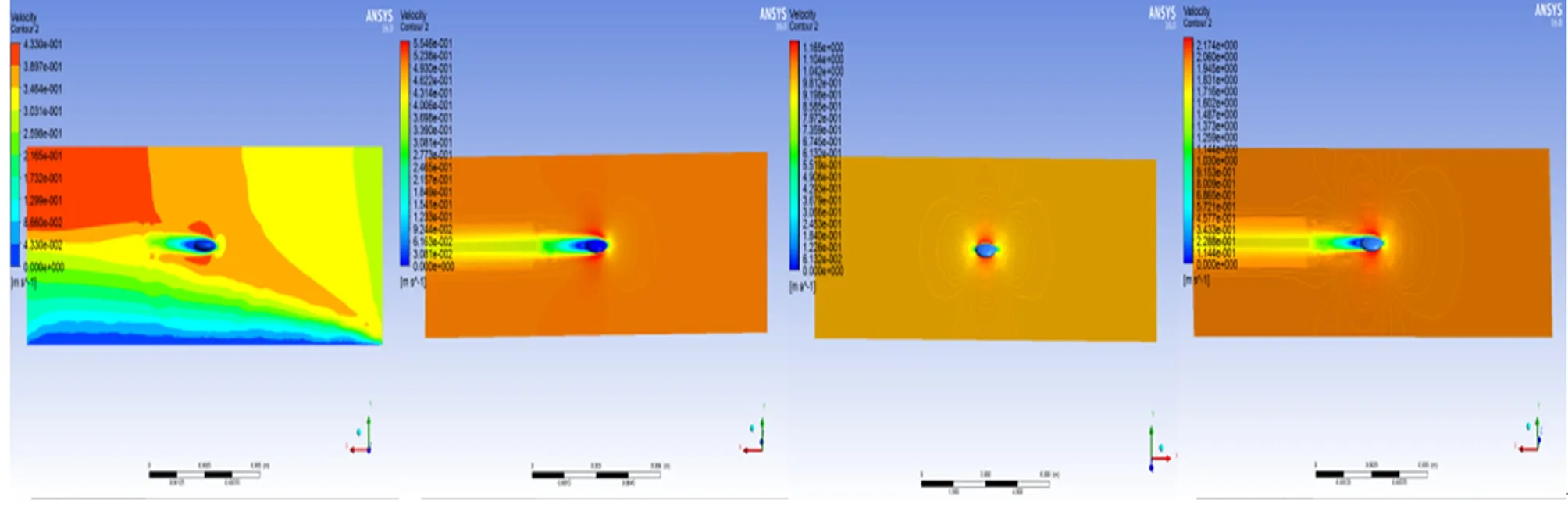
图5 ESV0.1~ESV2.0定常流动速度云图
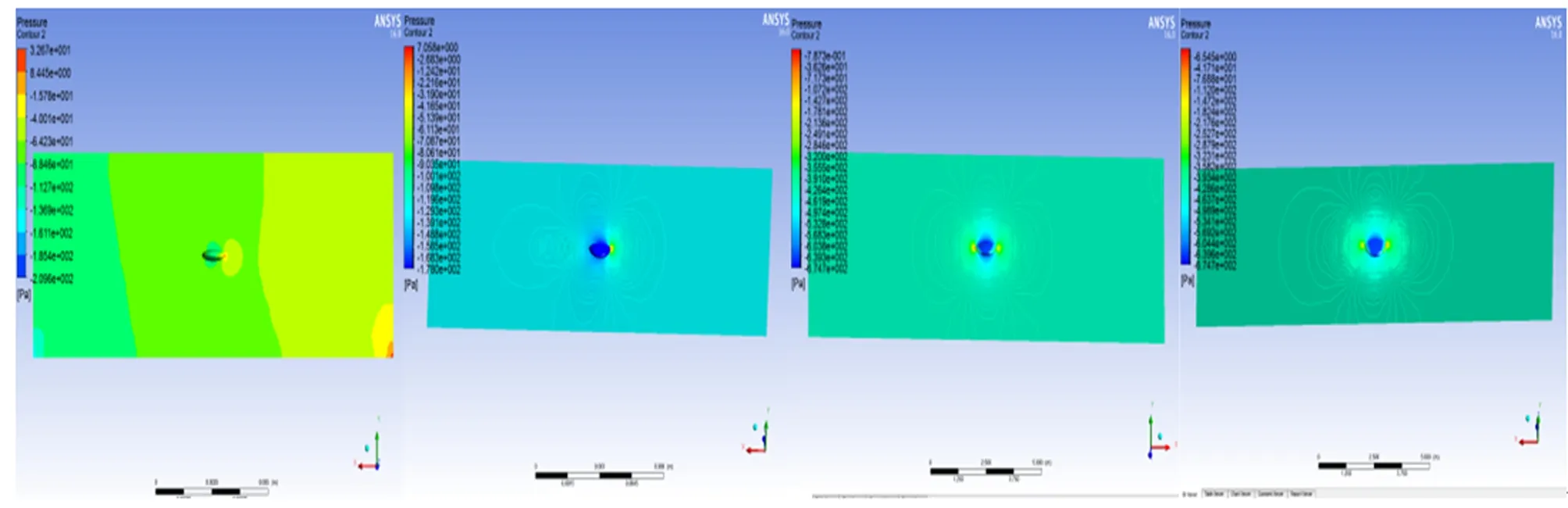
图6 ESV0.1~ESV2.0定常流动压力云图

图7 ESV0.1~ESV2.0定常流动速度矢量图
2.2.3 非定常工况
表2为试验非定常工况各参数的取值。
2.2.4 非定常工况云图
图8为EUSV0.1~EUSV2.0非定常流动速度云图。图9为EUSV0.1~EUSV2.0非定常流动压力云图。图10为EUSV0.1~EUSV2.0非定常流动速度矢量图。

表2 试验非定常工况
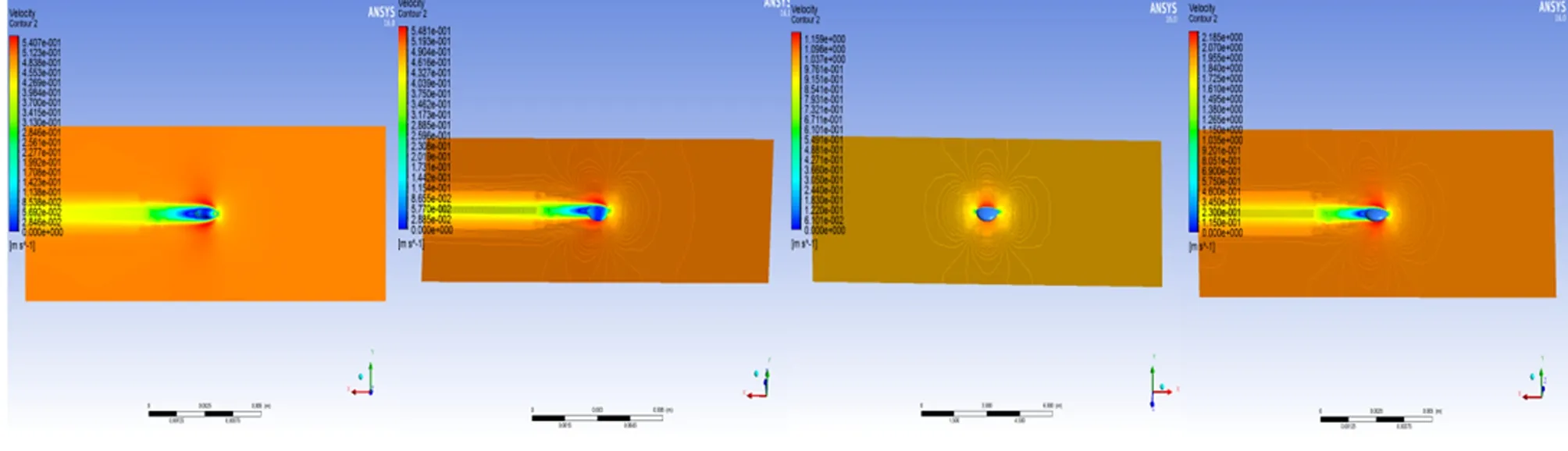
图8 EUSV0.1~EUSV2.0非定常流动速度云图
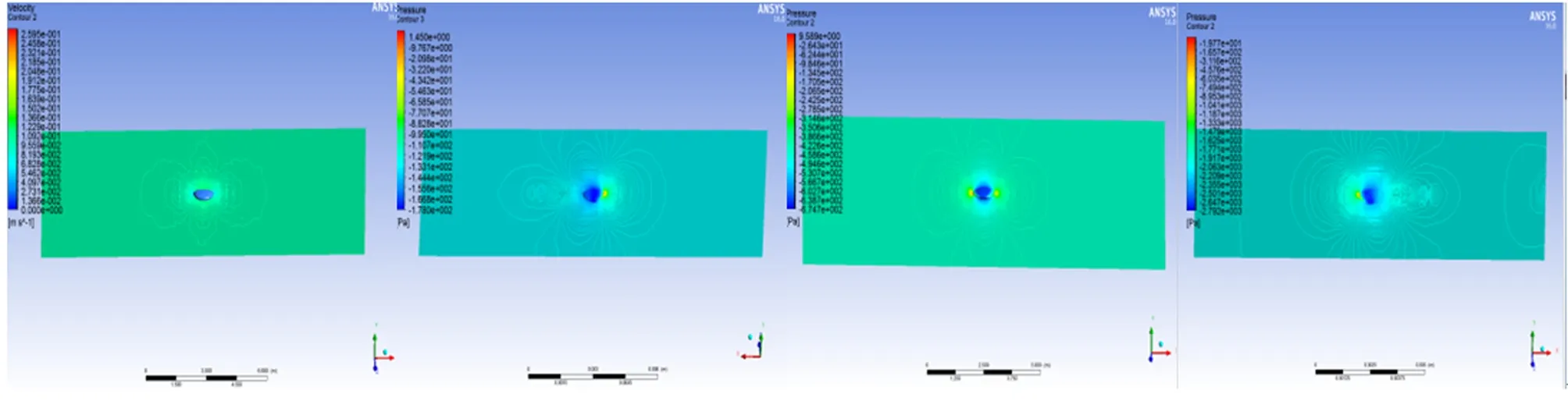
图9 EUSV0.1~EUSV2.0非定常流动压力云图
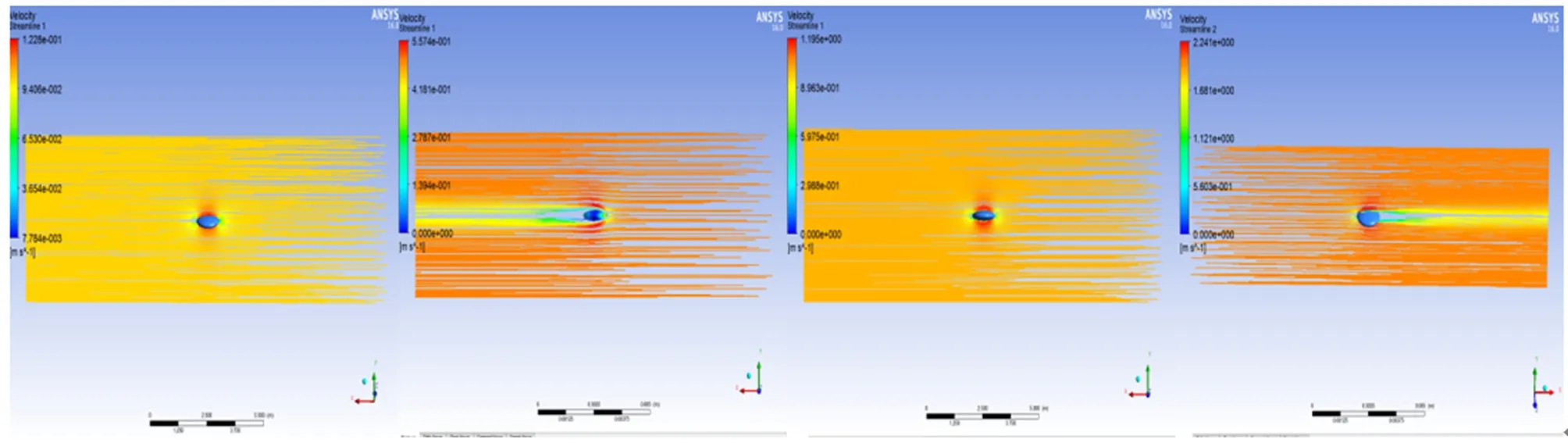
图10 EUSV0.1~EUSV2.0非定常流动速度矢量图
3 试验结果分析
利用FLUENT软件对上述模型进行计算求解,对定常和非定常在不同工况下外流场压力分布、速度分布及位能分布进行数据采集,以下只是收集速度为1 m/s流线上的位能、势能、动能。由于数据过多其他速度流线依此类推,工况代号ESV1.0L1/ EUSV1.0L1中,“E”表示椭圆形滑翔器,“S”表示定常流,“US”表示非定常流,“V1.0”表示速度,“L1”表示1号取样流线,MRE为平均值误差,RMSE为均方根误差。
3.1 定常流动流线上伯努利方程计算结果
表3为ESV1.0L1计算结果。表4为ESV1.0L2计算结果。表5为ESV1.0L3计算结果。表6为ESV1.0L4计算结果。表7为ESV2.0L5计算结果。
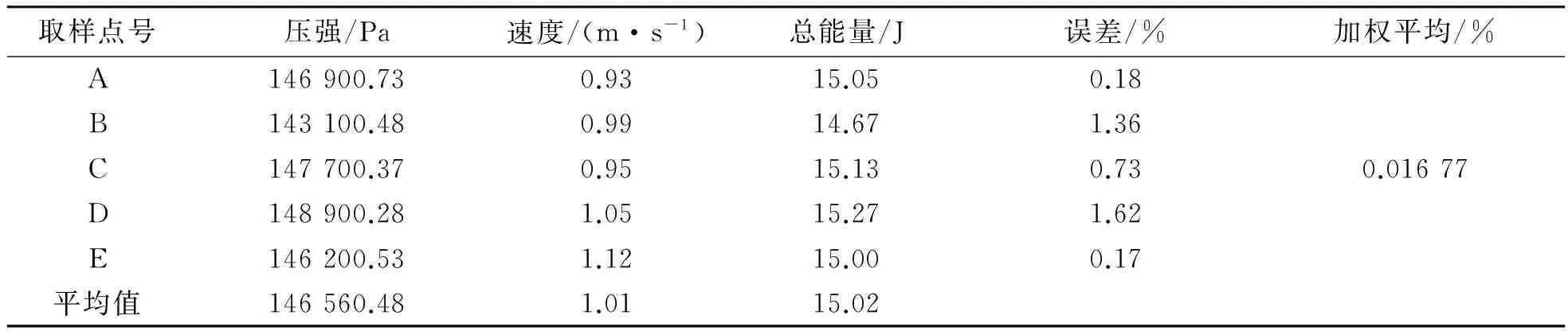
表3 ESV1.0L1计算结果
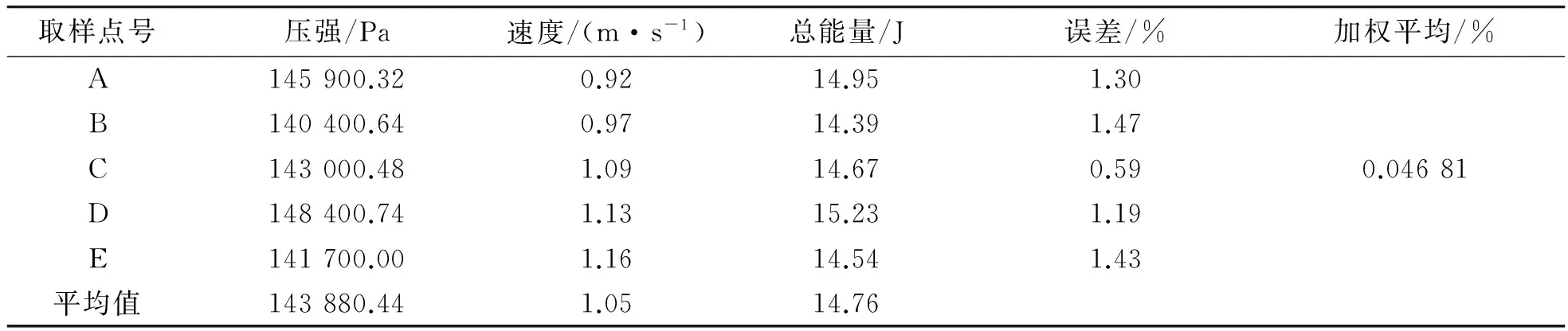
表4 ESV1.0L2计算结果
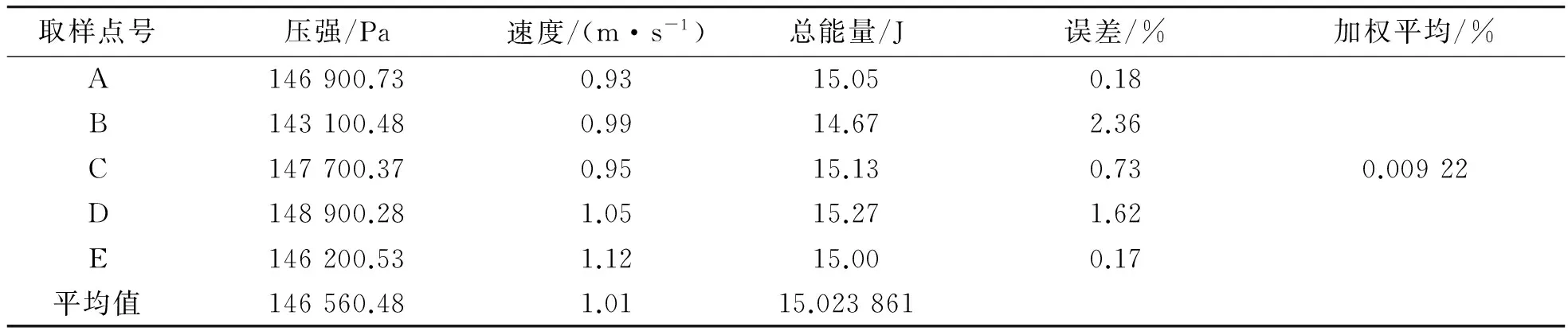
表5 ESV1.0L3计算结果
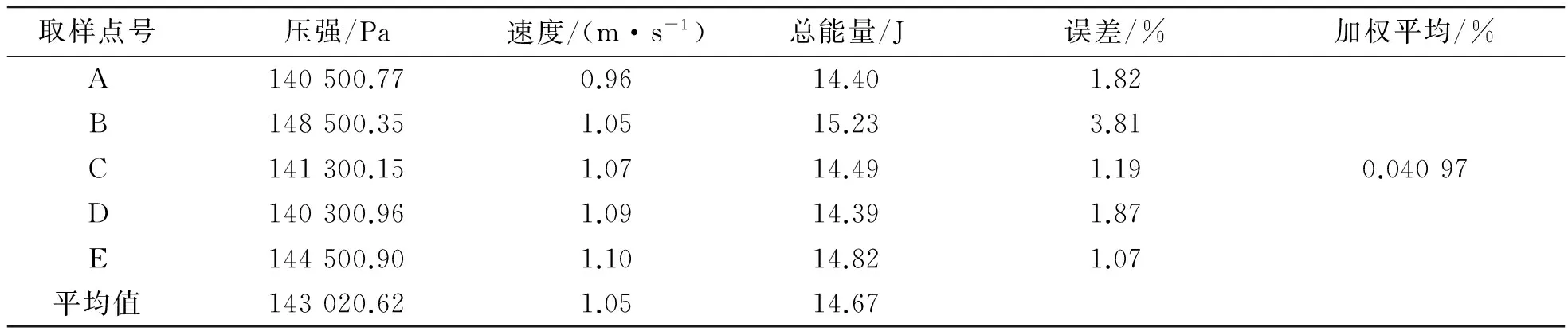
表6 ESV1.0L4计算结果
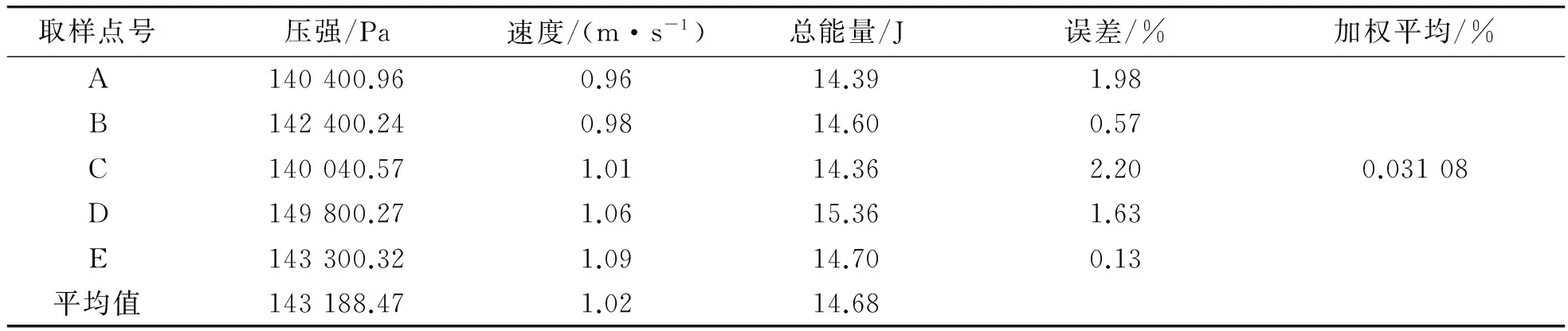
表7 ESV2.0L5计算结果
定常流动:由伯努利方程式(7)得:表3中A,B,C,D,E点的总能量(15.05~15.00 J)在误差的范围内相等,即是同一流线上不同点的总能量在误差的范围内相等,且均方根误差在0.016 677%,高度验证了伯努利方程。
将表4~表7的位能、势能、动能代入伯努利方程(7),可得出表中A,B,C,D,E点的总能量在误差的范围内相等,也即是同一流线上不同点的总能量在可接受的误差范围内相等,且均方根误差也非常地小,这样高度验证了伯努利方程。
3.2 非定常流动流线上伯努利方程计算结果
表8为EUSV1.0L1计算结果。表9为EUSV1.0L2计算结果。表10为EUSV1.0L3计算结果。表11为EUSV1.0L4计算结果。表12为EUSV1.0L5计算结果。
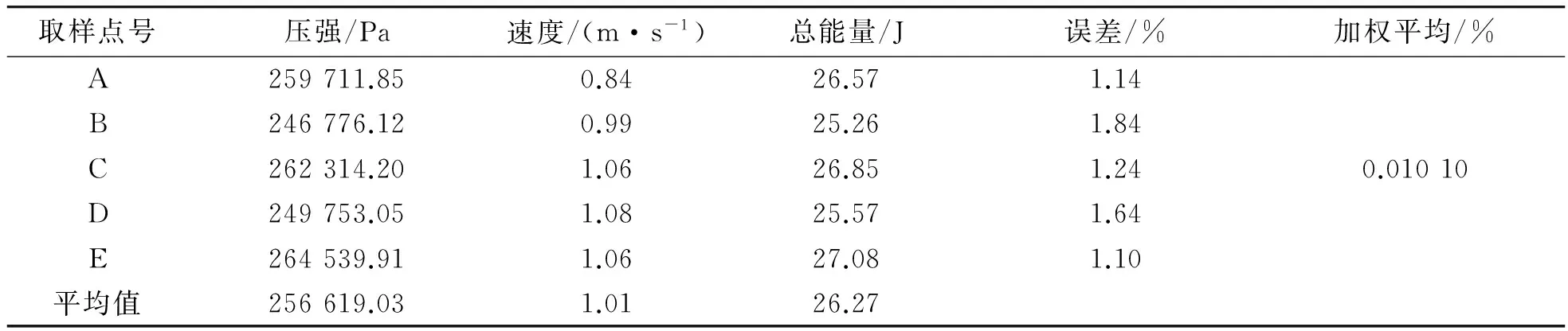
表8 EUSV1.0L1计算结果
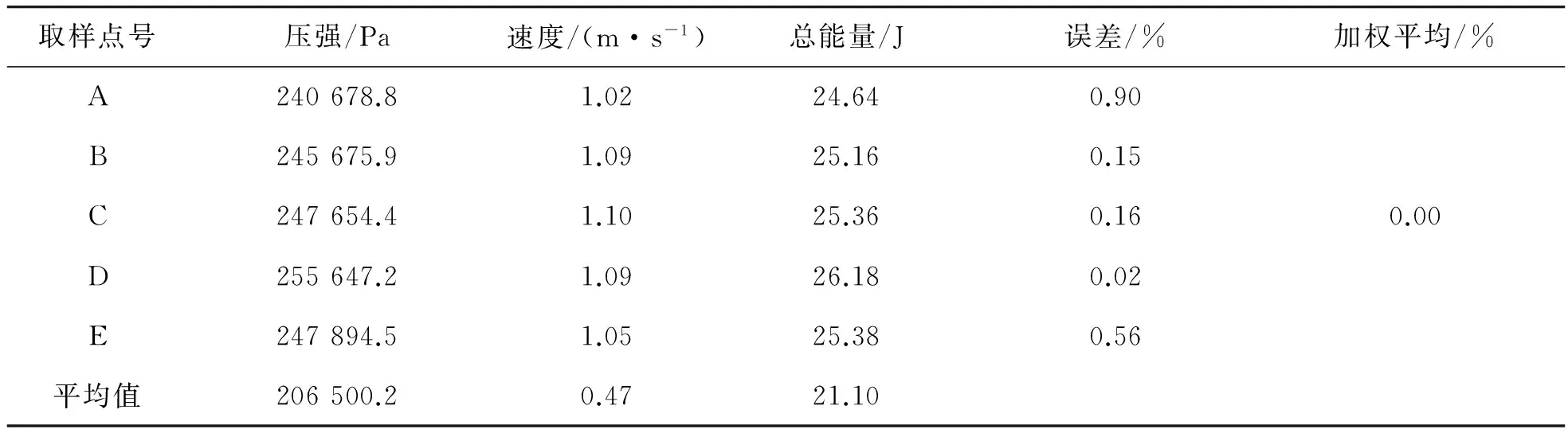
表9 EUSV1.0L2计算结果
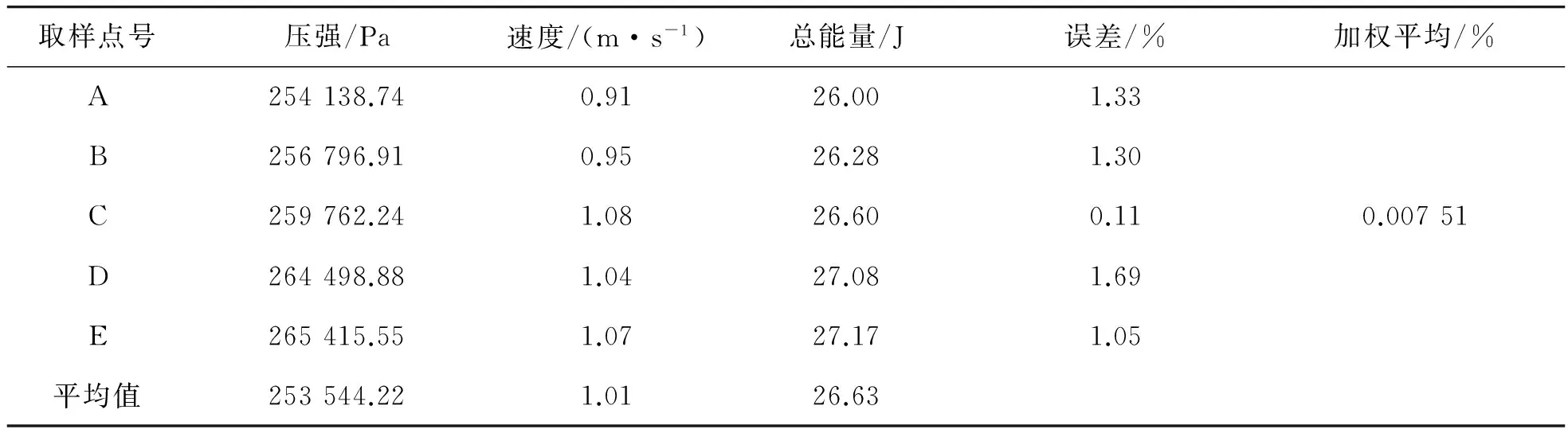
表10 EUSV1.0L3计算结果
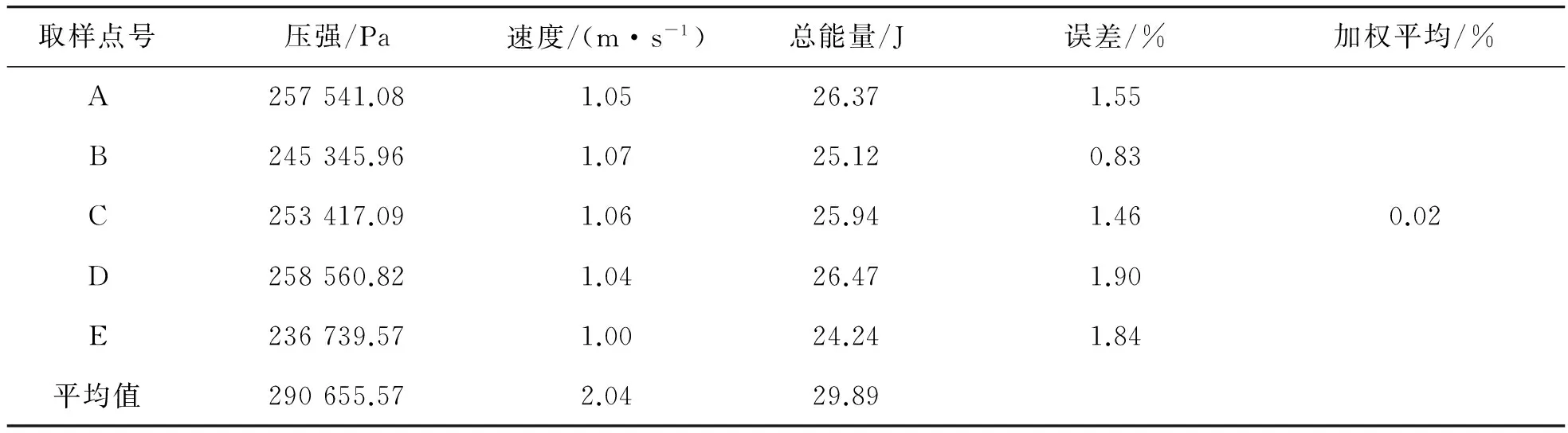
表11 EUSV1.0L4计算结果
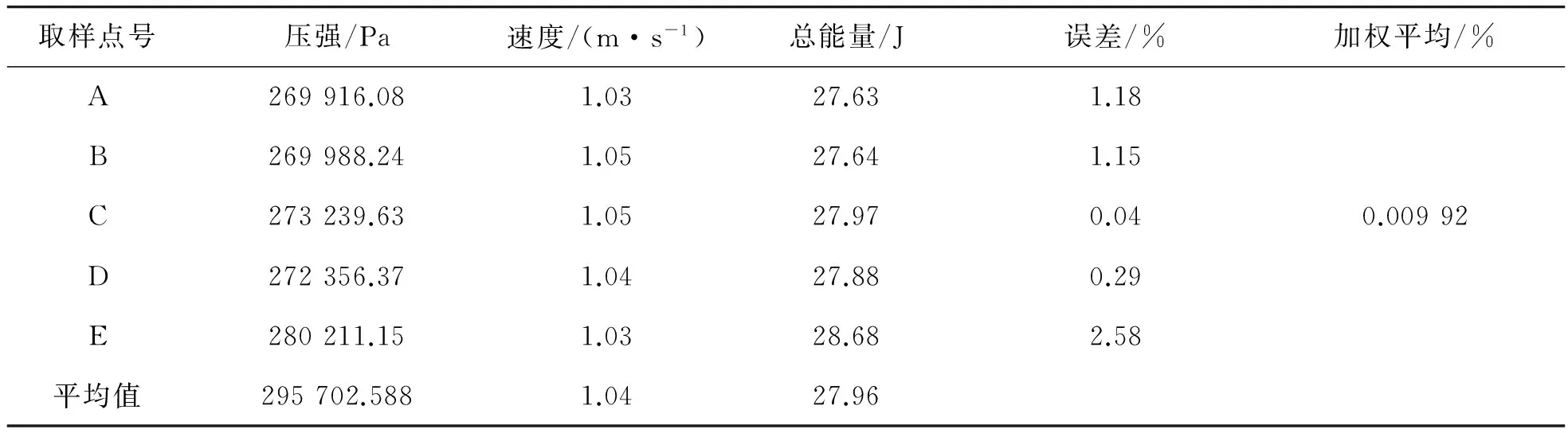
表12 EUSV1.0L5计算结果
根据伯努利方程式(7),表8中A,B,C,D,E点的总能量(26.57~27.08 J)在误差的范围内相等,即是同一流线上不同点的总能量在误差的范围内相等,且均方根误差在0.010 10%,高度验证了伯努利方程。
将表9~表12的位能、势能、动能分别代入伯努利方程式(7)中,可得出表中A,B,C,D,E点的总能量在误差的范围内相等,即是在非定常流时,同一流线上不同点的总能量在可接受的误差范围内相等,且均方根误差也非常地小,同样高度验证了伯努利方程。
4 结语
通过利用FLUENT 软件对椭圆形水下滑翔器在定常和非定常2种不同状态下的流场进行数值模拟,得到2种状况下外流场流线分布情况,验证了伯努利方程。分析表4~表7可知,在定常流时,同一速度、同一流线上不同取样点的动能和压能值之和稳定在一个常数之间,误差<2%,且加权平均均方根误差(RMSE )<0.04%;通过分析表8~表12可知,在非定常流时,同一速度、同一流线上不同取样点的动能和压能值之和也稳定在一个常数之间,误
[][]
差<3%,且加权平均均方根误差(RMSE)<0.02%。
由此证明伯努利方程是高度成立的,通过FLUENTL软件的数值模拟,可得本设计的椭圆形水下滑翔器满足一般的水动力性能要求,为进一步分析其水动力性能打下坚实基础。
[1] 徐爱英.伯努利方程的推导[J].科技信息,2012,4:157.
[2] 姚晓玲,宋世军.伯努利方程验证实验及装置改进[J]. 河北北方学院学报(自然科学版),2014,30(1):13-17.
[3] 陶苏玉.伯努利方程剖析[J].山东电大学报,2000,1:58-59.
[4] 徐铭.伯努利方程的适用条件分析[J]. 安阳大学学报(综合版),2002,2:36-37.
[5] 许俭.伯努利方程教学难点与对策分析[J].经营管理者,2015,12Z:488.
[6] 陶永祥.一类伯努利方程的简单解法[J].牡丹江大学学报,2013,8:117-118.
[7] 巴燕燕,张晓燕.伯努利方程在不同条件下各项物理意义的讨论[J]. 内蒙古民族大学学报(自然科学版),2008,3:260-261.
Bernoulli Verification of Elliptic Underwater Glider Based on FLUENT CFD
OU Qibin1, HUANG Ji1, OU Qiming2
(1.Ocean Engineering Academy, Guangdong Ocean University, Zhanjiang 524088,Guangdong, China; 2.College of Computational Sciences, Zhongkai University of Agriculture and Engineering, Guangzhou 510550, Guangdong, China)
The numerical simulation is carried out to elliptic underwater glider in different flow velocity by CFD FLUENT. The Bernoulli equation in fluid mechanics is used to verify the physical field around the elliptical buoy. It can be concluded that, at the same streamline, unit weight of the fluid, the total mechanical energy is approximately equal. The sum of kinetic energy, stress energy, location potential energy is a constant value at the same streamline of different points, and the error is less than 3%. As a result, Bernoulli equation is established at any point of the whole flow field.Therefore, elliptic underwater gliders are satisfied to ordinary hydrodynamic performance.
Bernoulli equation; FLUENT; numerical simulation; elliptic underwater glider
大学生创新创业训练计划立项项目(CXXL2016021);广东省大学生攀登计划项目(pdjh2016b0239);广东省大学生攀登计划项目(pdjh2016b0232)
欧启彬(1994-),男,本科,研究方向为船舶与海洋工程
1001-3878(2017)02-0028-07
U661
A

