N次达布变换和KdV6方程的孤子解*

李 红，王鑫，李吉娜

(中原工学院)

N次达布变换和KdV6方程的孤子解*

李 红，王鑫，李吉娜

(中原工学院)

构造了多参数KdV6方程的N次达布变换.在应用中，可以得到2N－扭状孤子解.此外，利用设置一些参数为零的约简方法，2N－扭状孤子解可以衰减到2N－1，2N－2，甚至是1－扭状孤子解.

达布变换;KdV6方程;扭状孤子解

0 引言

近些年，一个新的可积KdV6方程引起学者们的兴趣［1－7］.

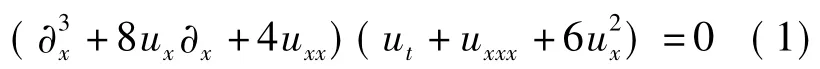
最初，Karasu－Kalkanli和他的同事在研究经典的6阶非线性波动方程时发现方程［1］，这个方程不属于任何已知的可积系统［1，7］.他们取得了许多重要结果，例如，Lax表示，auto－Backlund变换，双哈密顿结构和守恒定律［2］.此外，Zhaqilao等［5］对方程(1)构造1－次达布变换，通过N次达布变换，得到其N－扭状孤子解.Geng和Xue［7］分别用逆方法和代数曲线理论构造方程(1)的N－孤子解和拟周期解，更进一步的表明方程(1)拥有良好的数学结构.

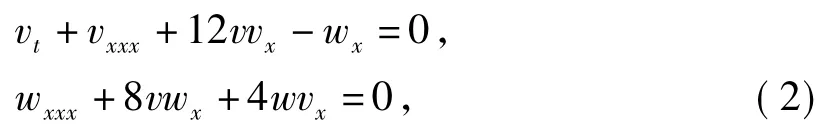
上式称作耦合的不完整变形KdV方程［1，3］，该方程同样被许多学者研究.例如，SahadeVan和NalinideVi［3］给出该方程的Lie点对称，非局部和主要对称性以及一个显式孤子特解.基于换向表示法，Zhou［4］提出构造混合结构的零曲率方程，并证明方程(2)属于混合的KdV结构，表明方程(2)完整的可积性.众所周知，寻找非线性偏微分方程的精确解是一个重要和复杂的任务.有许多对称方法如 Hirota双线性方法，达布变换(DT)，对称逼近，代数几何方法，延拓双曲正切函数法等等.其中，DT是最直接且有效的方法之一，若有一个最初的平凡子解，直接用DT方法可以得到显式非平凡孤子解.

据所知，N次DT被称作KdV6方程(1)以及耦合不完整变形KdV方程目前还没有被研究.若能构造N次DT，就可以不经过冗长的迭代便可得到基于子解的显式多重孤子解和N次DT.该文旨在构造KdV6方程(1)和耦合不完整变形KdV方程的N次DT，不经过冗长的迭代，直接得到新的精确解和子解.

该文结构如下:第二部分，给出基于DT的Schrodinger谱问题，方程(1)和(2)的N次DT，并从空间谱问题到时域的角度给出详细的证明.第三部分，通过应用N次DT得到方程(1)的2N扭状孤子解.通过采用设置一些参数为零的约简方法，2N－扭状孤子解可以衰减到2N－1，2N－2，甚至是1－扭状孤子解.

1 达布变换

在这一部分，首先考虑谱题

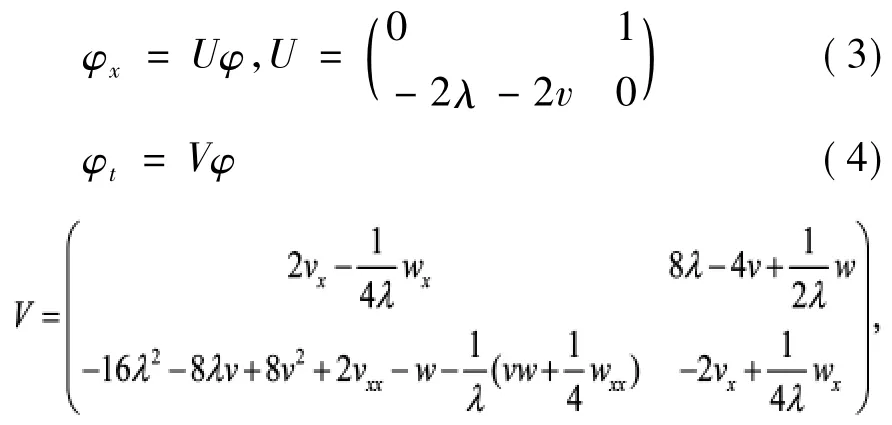
这里λ是谱参数，v，w是电位.又因为φxt=φtx，自然地，得到方程(2)和(1).

为了构造方程(1)和(2)的N次DT，接下来介绍规范变换

(3)和(4)的Lax表示可以变换为

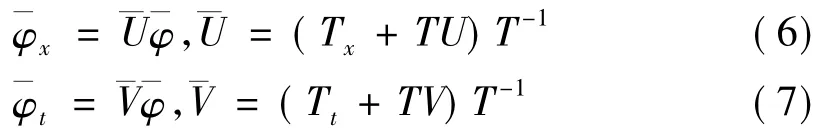
如果上述新的谱问题和传统类型相同，称作规范变换的达布变换.为此，基于DT的Schrodinger谱问题，假设

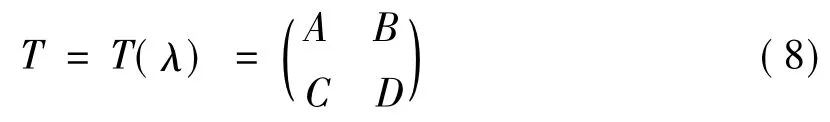
其中

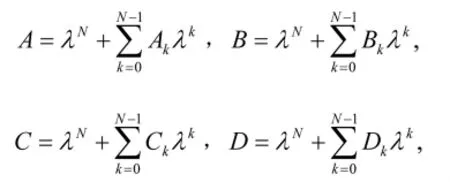
设CN=－2BN－1，Ak，Bk，Ck，Dk(0≤k≤N－1)是如下给定的线性代数系统

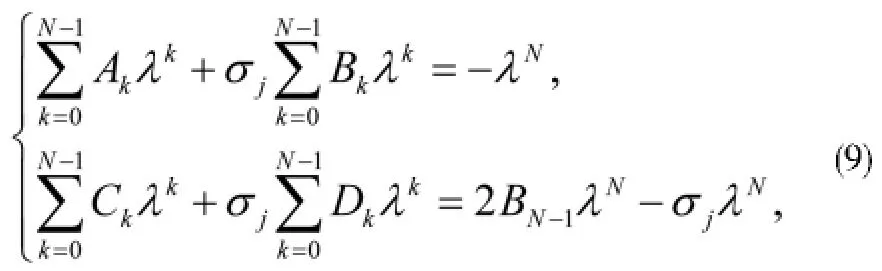
其中

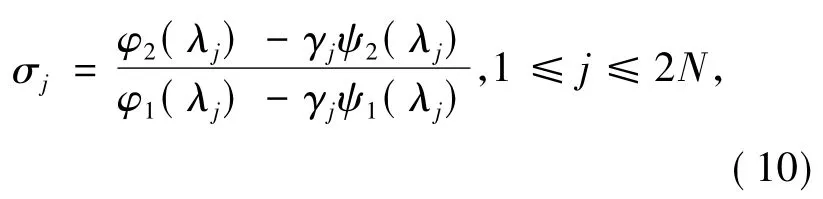
这里λj，γj，(1≤j≤2N)是任意参数，这样使得(9)的系数非零.φ(λj)=(φ1(λj)·φ2(λj))，ψ(λj)=(ψ1(λj)，ψ2(λj))是方程(3)和(4)的两个基本解.接下来达布矩阵(8)可以由这个线性代数系数确定.

根据(8)，可以知道detT(λ)是λ的2N次多项式，

detT(λj)=A(λj)D(λj)－B(λj)C(λj)，此外，由(9)，有

A(λj)=－σjB(λj)，C(λj)=－σjD(λj)，意味着

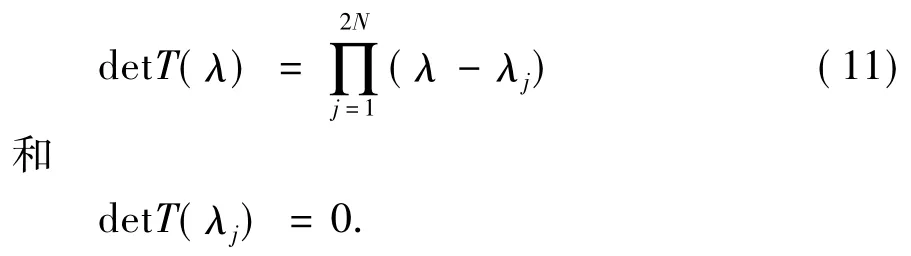
综上所述，可以推导如下命题.

命题1除了初始变换，由(6)确定的矩阵珚U和U有同样的形式，

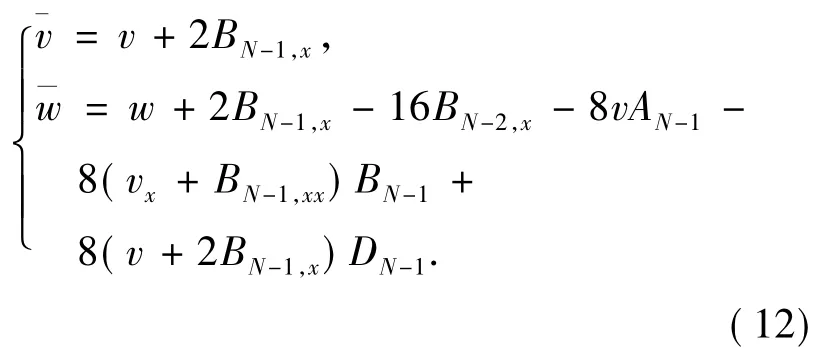
证明令

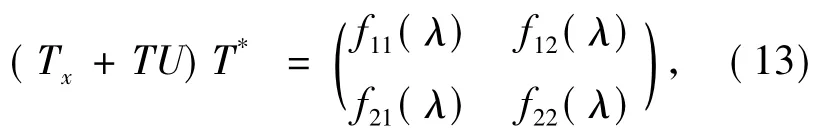
这里T*是T的伴随矩阵.易知fij是λ的2N次或2N+1次多项式.从Riccati方程

命题2除了用DT将旧势映射到新势，由(7)确定的矩阵有同样的形式.

证明首先列举已经证明过的(14)中一些有用的表示

对比(16)的系数λN－1，λN，λN－1和λN－2，先后得到有

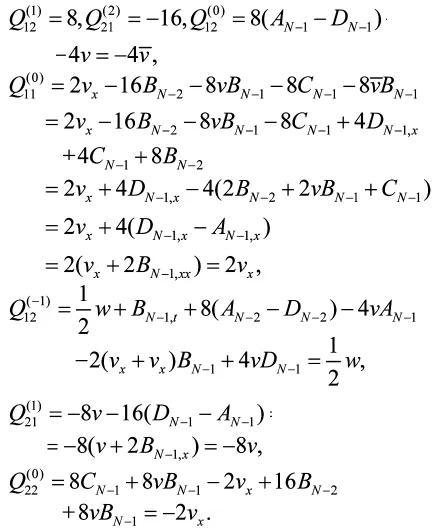
综上所述，经过复杂的计算，有

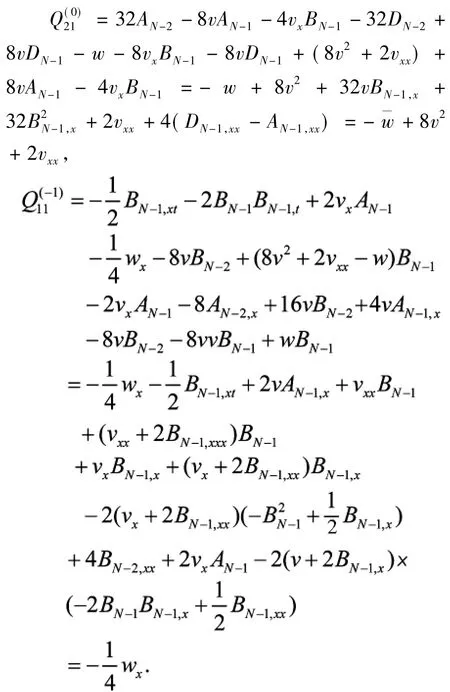
同样，通过非常复杂但是直接的计算，也可以验证

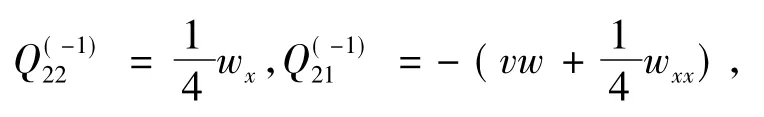
在这里不再赘述.

根据命题1和2，知道在(8)和(12)变换下，(6)和(7)新的Lax表示同(3)(4)有相同的形式，这说明新的Lax表示同样可以引导耦合的非完整变形方程KdV方程(2).变换(12)称作耦合的非完整变形方程KdV方程的达布变换.因此自然地，得到下面的命题.

命题3耦合的非完整变形方程KdV方程的解(v，w)在达布变换(12)下映射到新解，达布变换矩阵是由代数系统(9)唯一确定的.

最后，给出最重要的命题.

命题4通过N次DT，，KdV6方程的解u可以生成新的解.

2 KdV6方程的多重扭状解

在这一部分，用N次DT构造KdV6方程新的显式解.从一个平凡解u=0开始，那么方程(2)的平凡解是v=0，w=0.将v=0，w=0代入Lax表示(3)和(4)，基本解可以选为

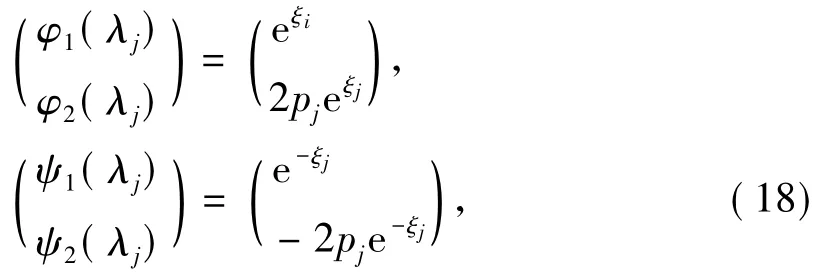
通过(10)，有

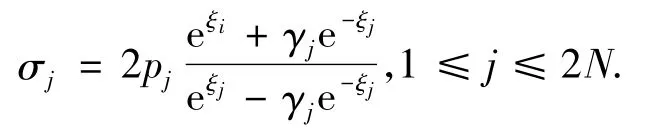
选择适当的参数可以使(9)的系数非零，通过求解代数系统(9)，得到

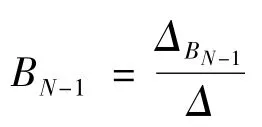
其中

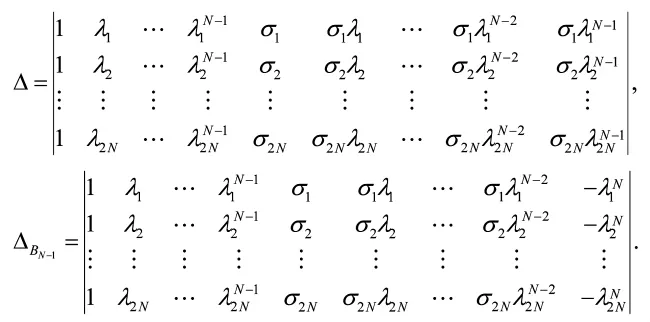
因此，KdV6方程新的精确解的序列自然地表示为

接下来，讨论N=1和N=2两种情况.

(1)当N=1时有，

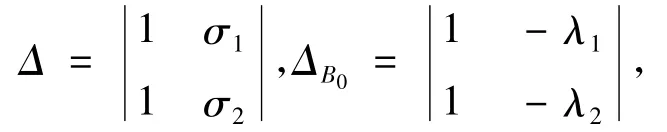
那么认为

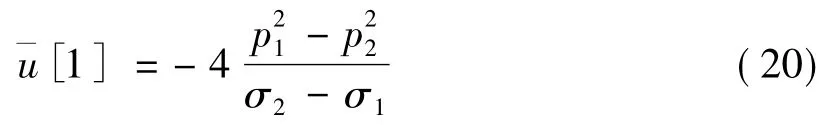
这里

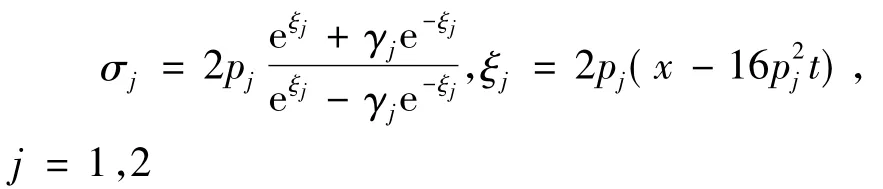
通过选择合适的参数γ1，γ2≠0使得Δ非零，可得到没有奇异点的2－扭状孤子解，若令γ2≠0，上述解将衰减到1－扭状孤子解.

(2)当N=2时有

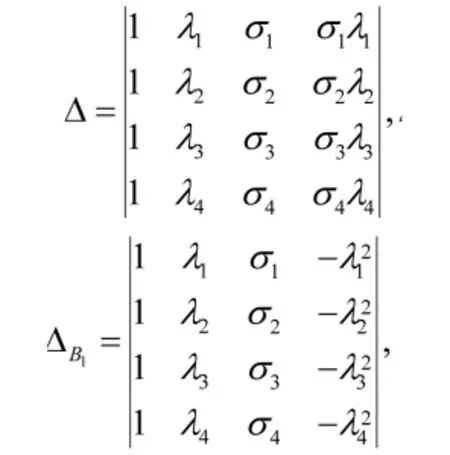
KdV6方程(1)的新精确解可以表示为

其中

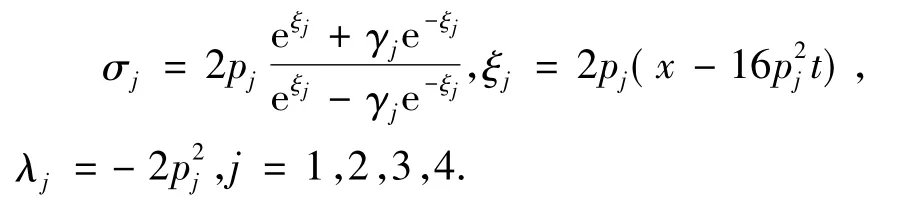
通过选择合适的参数γj≠0(j=1，2，3，4)，使得Δ非零，可得到没有奇异点的4－扭状孤子解，此外，若令γj=0(j=2，3，4)，上述解将衰减到3，2甚至1－扭状孤子解.

3 结束语

在该文中，构造KdV6方程(1)和耦合不完整变形KdV方程(2)的N次DT，不用经过冗长的迭代，便可直接得到新的精确解和子解.在应用中，得到KdV6方程(1)的2N－扭状孤子解.此外，通过采用设置一些参数为零的约简方法，2N－扭状孤子解可以衰减到2N－1，2N－2，甚至是1－扭状孤子解.

［1］Karsau－Kalkani A，et al.A new integrable generalization of the Korteweg－de Vries equation.J Math Phys，2008，49: 073516.

［2］Kupershmidt B A.KdV6:An integrable system.Phys Lett A，2008，372:2634－2639.

［3］Sahadevan R，Nalinidevi L.Similarity reduction，nonlocal and master symmetries of sixth order Korteweg－deVries equation.J Math Phys，2009，50，053505.

［4］Zhou R G.Mixed hierarchy of soliton equations.J Math Phys，2009，50:123502.

［5］Zha Qilao，Sirendaoreji.N－soliton solutions of the KdV6 and mKdV6 equations.J Math Phys，2010，51:113507.

［6］Wen X Y，et al.Darboux transformation and explicit solutions for the integrable sixth－order KdV equation for nonlinear waves.Appl Math Comput，2011，218:55－60.

［7］Geng X G，Xue B.N－soliton and quasi－periodic solutions of the KdV6 equations.Appl Math Comput，2012，219: 3504－3510.

［8］Hirota R.The Direct Method in Soliton Theory.Cambridge: Cambridge University Press，2004:1－109.

［9］Hu X B.Nonlinear superposition formula of the Novikov－Veselov equation.J Phys A:Math.Gen，1994，27:1331－1338.

［10］Gu C H，et al.Darboux Transformation in Soliton Theory and Its Geometric Applications Shanghai:Science and Technology Press，1999.34－40.

［11］Matveev V B，Shalle M A.Darboux Transformation and Solitons.Berlin:Springer，1991.97－208.

［12］Fan E G.Darboux transformation and soliton－like solutions for the Gerdjikov－Ivanov equation.J Phys A:Math.Gen，2000，33:6925－6933.

［13］Fan E G.A differential－difference hierarchy associated with relativistic Toda and Volterra hierarchies.Phys Lett A，2008，372:4578－4585.

［14］Geng X G.Darboux transformation of the discrete Ablowitz－Ladik eigenvalue problem.Acta Math Sci，1989，9:21－26.

［15］Li W M et al.Darboux transformation of a nonlinear evolution equation and its explicit solutions，Acta Math Sci，2011，31B:1457－1464.

［16］Liu Q P.Darboux Transformations for Supersymmetric Korteweg－de Vries Equations.Lett Math Phys，1995，35:115－122.

［17］Xue B and Wang X.The Darboux Transformation and New Explicit Solutions for the Belov－Chaltikian Lattice.Chin Phys Lett，2012，29:100201.

［18］Qu C Z.Potential symmetries to systems of nonlinear diffusion equations.J Phys A:Math Theor，2007，40:1757－1773.

［19］Lou S Y，Ma H C.Non－Lie symmetry groups of(2+1)－dimensional nonlinear systems obtained from a simple direct method.J Phys A:Math Gen，2005，38:L129－L137.

［20］Dong Z Z，Chen Y.Symmetry Reductions and Exact Solutions of Blaszak－Marciniak Four－Field Lattice Equation.Commun Theor Phys，2010，54:389－392.

［21］Zhang D J，Chen S T.Symmetries for the Ablowitz－Ladik hierarchy:I.Four－potential case.Stud Appl Math，2010，125:393－418.

［22］Chen D Y，Zhang D J.Lie algebraic structures of(1+1)－dimensional Lax integrable systems.J Math Phys，1996，37: 5524－5538.

［23］Geng X G，Xue B.Soliton solutions and quasiperiodic solutions of modified Korteweg－de Vries type equations.J Math Phys，2010，51:063516.

［24］Fan E G.Quasi－periodic waves and an asymptotic property for the asymmetrical Nizhnik－Novikov－Veselov equation.J Phys A:Math Theor，2009，42:095206.

［25］Fan E G.Extended tanh－function method and its applications to nonlinear equations.Phys Lett A，2000，277:212－218.

［26］Yan Z Y.New explicit travelling wave solutions for two new integrable coupled nonlinear evolution equations.Phys Lett A，2001，292:100－106.

N－Fold Darboux Transformation and New Soliton Solutions of One Kdv6 Equation

Li Hong，Wang Xin，Li Jina
(Zhongyuan University of Technology)

N－fold Darboux transformation with multiparameters of one KdV6 equation is constructed with the aid of the gauge transformation.As appilication，2N －kink solition solutions are obtained.Furthermore，by using reduction approach of setting some parameters to be zero，the 2N －kink solitonsolutions can be reduced into 2N－1，2N－2，or even one－kink soliton solutions，respectively.

Darboux transformation;KdV6 equation;Kink soliton solution

35Q51;37K40

:A

:1000－5617(2017)01－0008－05

(责任编辑:李家云)

2016－12－25

*河南省自然科学基金项目(152300410227);河南省高等学校重点科研项目(15B110012，17A110036)