一类带有时滞的非局部反应扩散系统波前解的存在性

刘桂荣,王志梅

(山西大学 数学科学学院,山西 太原 030006)

一类带有时滞的非局部反应扩散系统波前解的存在性

刘桂荣,王志梅

(山西大学 数学科学学院,山西 太原 030006)

考虑一类带有时滞的非局部反应扩散系统。通过构造系统的上解和下解,并利用Schauder不动点定理证明了存在正常数c*(τ1,τ2,τ3),当c≥c*(τ1,τ2,τ3)时,该反应扩散系统存在波速为c的波前解。

非局部反应扩散系统;波前解;上下解;Schauder不动点定理

0 引言

物理学、化学和生物学中的许多问题都可以用反应扩散方程来刻画[1]。近年来,行波解作为反应扩散方程的一个重要研究内容受到了国内外学者的广泛关注,并发表了一些较好的成果[2-4]。文献[5]研究如下带有时滞的反应扩散系统

(1)

注意到系统(1)中Laplace算子定义的扩散项只能反映空间上的局部作用,但对一个生物种群来说,该种群中的个体会在一个较大的范围内移动,因此文[6]考虑了下列带有时滞的非局部反应扩散系统

(2)

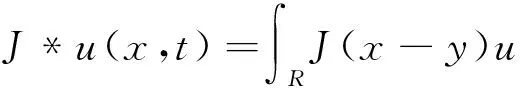
人口由静止阶段转化成活动阶段需要一段时间,活动阶段转化为静止阶段也需要一段时间,因而这一变化过程需要考虑时滞的影响。为此我们建立下列带有多个时滞的非局部反应扩散系统

(3)

(H2)f∈C2([0,K]2,R),f(0,0)=f(K,K)=0,对任意u∈(0,K),f(u,u)>0,且对任意(u,v)∈[0,K]2,∂2f(u,v)≥0,其中K>0为常数。

(H3)对任意(u,v)∈[0,K]2,∂1f(0,0)u+∂2f(0,0)v≥f(u,v),∂1f(K,K)+∂2f(K,K)<0.

1 波前解的存在性

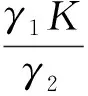
(u(x,t),v(x,t))=(U(ξ),V(ξ))

的行波解,其中ξ=x+ct,c>0为行波速度,(U,V)∈C1(R,[0,K]×[0,K0]).当U(·),V(·)单调时,(U,V)为系统(3)的波前解。

将(u(x,t),v(x,t))=(U(ξ),V(ξ))代入(3),有

(4)

其边界条件为

(U(-∞),V(-∞))=(0, 0), (U(∞),V(∞))=(K,K0).

(5)

求解(4)的第二个方程并结合V(-∞)=0可得,

s.

(6)

当U(-∞)=0,U(∞)=K时,由(6)可知V(-∞)=0,V(+∞)=K0.将(6)代入(4)的第一个方程,可得

cU′(ξ)=D[J*U(ξ)-U(ξ)]+f(U(ξ),U(ξ-cτ1))-γ1U(ξ)+

(7)

其边界条件为

U(-∞)=0,U(∞)=K.

(8)

从而可知下列引理成立。

引理1 对任意U∈C1([0,K]),若U是(7)与(8)的解,则(U(x+ct),V(x+ct))是(3)的单调不减的波前解,其中V(ξ)满足(6)。

因此,为了得到系统(3)的波前解的存在性,只需考虑(7)与(8)的单调不减的解的存在性。

定义算子F∶C(R,[0,K])→C(R,R),

(9)

易证Fφ满足:c(Fφ)′(ξ)=-β(Fφ)(ξ)+(Hφ)(ξ),从而F的不动点为(7)的解。

类似于文[6]引理2.2的证明,可得下列引理成立。

引理2 (i)对任意φ1,φ2∈C(R,[0,K]),若φ1≤φ2,则(Hφ1)(ξ)≤(Hφ2)(ξ),(Fφ1)(ξ)≤(Fφ2)(ξ),ξ∈R.

(ii)对任意φ∈C(R,[0,K]),若φ关于ξ单调不减,则Hφ,Fφ也关于ξ单调不减。

显然(Bμ(R,R),|·|μ)是一个Banach空间。

注意到(7)在U(ξ)=0处的线性化系统对应的特征方程为:

对任意λ>0，

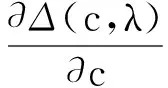
对任意c>0,

由上述结果可以得出下面的引理。

引理3 设(H1)-(H3)成立,则存在一个正数c*(τ1,τ2,τ3),使得下列结果成立。

(i)若00,则Δ(c,λ)>0.

(ii)若c=c*(τ1,τ2,τ3),则Δ(c,λ)=0有两个相等正实根λ1(c)=λ*=λ2(c).

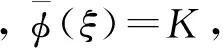
当ξ≤ξ*时,

-qΔ(c,γλ1(c))eγλ1(c)ξ-4L(e2λ1(c)ξ-2qe(1+γ)λ1(c)ξ+q2e2γλ1(c)ξ)≥

(-qΔ(c,γλ1(c))+4L-4Lq)eγλ1(c)ξ≥0，

对任意c>c*(τ1,τ2,τ3), 定义

显然Γ是Bμ(R,R)的非空闭凸子集。

引理5 若(H1)-(H3)成立, 则当c>c*(τ1,τ2,τ3)时,算子F∶Γ→Γ有不动点。

(Fφ)(ξ).

定理1 若(H1)-(H3)成立,则存在c*(τ1,τ2,τ3)>0,使得对任意c≥c*(τ1,τ2,τ3),系统(3)存在单调不减的波前解(u(x,t),v(x,t))=(U(x+ct),V(x+ct)),其中(U(·),V(·))满足(4)与(5)。

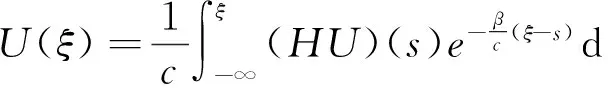
[1] 叶其孝.反应扩散方程引论[M].2版.北京:科学出版社,2011.

[2] Wang Z C,Li W T,Ruan S.Traveling Fronts in Monostable Equations with Nonlocal Delayed Effects[J].JDynDiffEquat,2008,20:573-607.DOI:10.1007/s10884-008-9103-8.

[3] Yu Z X,Yuan R.Existence and Asymptotics of Traveling Waves for Nonlocal Diffusion Systems[J].NonlinearScienceandNonequilibriumandComplexPhenomena,2012,45:1361-1367.DOI:10.1016/j.chaos.2012.07.002.

[4] Zhou K,Wang Q R.Traveling Wave Solutions in Delayed Nonlocal Diffusion Systems with Mixed Monotonicity[J].JournalofMathematicalAnalysisandApplication,2010,372:598-610.DOI:10.1016/j.jmaa.2010.07.032.

[5] Wu S L,Zhao H Q.Traveling Fronts for a Delayed Reaction-diffusion System with a Quiescent Stage[J].CommunNonlinearSciNumerSimulat,2011,16:3610-3621.DOI:10.1016/j.cnsns.2011.01.012.

[6] Zhou K,Lin Y,Wang Q R.Existence and Asymptotics of Traveling Wave Fronts for a Delayed Nonlocal Diffusion Model with a Quiescent Stage[J].CommunNonlinearSciNumerSimulat,2013,18:3006-3013.DOI:10.1016/j.cnsns.2013.04.025.

Existence of Traveling Wave Fronts for Delayed Nonlocal Diffusion System

LIU Guirong,WANG Zhimei

(School of Mathematical Sciences, Shanxi University,Taiyuan 030006,China)

This paper is concerned with the nonlocal reaction diffusion system.By using upper-lower solution approach and Schauder fixed point theorem, we prove that there exists a positive constantc*(τ1,τ2,τ3) such that for eachc≥c*(τ1,τ2,τ3) the system has a traveling wave fronts with speedc.

nonlocal reaction diffusion system;traveling wave fronts;upper-lower solution;Schauder fixed point theorem

10.13451/j.cnki.shanxi.univ(nat.sci.).2017.03.003

2017-05-16；

2017-06-01

国家自然科学基金(11471197);山西省自然科学基金(2014011005-1)

刘桂荣(1975-),男,山西吕梁人,博士，教授，研究方向:微分方程与动力系统。E-mail:lgr5791@sxu.edu.cn

O175

A

0253-2395(2017)03-0411-05