复杂网络传播动力学研究进展

靳祯,罗晓峰

(1.山西大学 复杂系统研究所,山西 太原 030006;2.山西大学 疾病防控的数学技术与大数据分析山西省重点实验室,山西 太原 030006;3.山西大学 计算机与信息技术学院,山西 太原 030006)

复杂网络传播动力学研究进展

靳祯1,2,罗晓峰1,3

(1.山西大学 复杂系统研究所,山西 太原 030006;2.山西大学 疾病防控的数学技术与大数据分析山西省重点实验室,山西 太原 030006;3.山西大学 计算机与信息技术学院,山西 太原 030006)

网络上的信息或者疾病传播问题是复杂网络研究的焦点之一,其不仅依赖于信息或者疾病自身的传播特征,而且依赖于网络的结构与演化,是疾病传播动力学与网络演化动力学的耦合过程,会产生十分复杂的动力学现象。文章主要介绍复杂网络上传播动力学的一些基本概念、建模与研究方法,主要包括基于对关系、度、节点和渗流理论等四类网络传播动力学模型以及复杂网络传播动力学建模与分析方面的主要进展。

复杂网络;对逼近;邻接矩阵;边仓室;渗流理论

0 引言

复杂网络作为一门新兴的学科,在近几十年发展迅速。自然界以及人类社会中存在的大量复杂系统都可以用网络来描述,几乎所有的系统都可以抽象成为网络模型,如Internet网、电力网、航空网、蛋白质网及生物链网等[1]。根据不同的网络特性,网络有不同的分类,如根据度分布,网络可分为规则网络(Delta度分布)、随机网络[2](泊松度分布)、无标度网络[3](幂率度分布)等;根据度的差异性大小,前两种网络称为均匀网络而无标度网络称为异质网络;若网络结构随时间不变,则称网络为静态网络,否则为动态网络。疾病或信息在群体行中的传播可以看成是特定网络结构上信息的传播及演化,既依赖于网络的度分布、聚类系数、相关系数、平均路径长度等拓扑结构又依赖于信息的传播特征,会产生复杂的动力学现象。近年来,复杂网络传播动力学方面的研究已经有了长足的发展,发现了大量与传统动力学有实质性差异的现象,如无标度网络上无阈值等现象[4]。本文将主要介绍静态网络上传播动力学方面的基本概念、建模思想、分析方法及其研究进展。下面先回顾一些基本的网络拓扑特征量[1]。

考虑一个节点规模为N的复杂网络,可以用简单的无向网络G=(V,E)来表示,V表示G的节点集,其元素为节点;E表示G的边集,其元素为边。网路G的邻接矩阵定义为

A=(aij)N×N,

(1)

该矩阵是一个N阶方阵,第i行j列的元素定义如下

(2)

网络中节点i的度ki为与节点i连接的边(邻居节点)的总数,任选一个节点其度为k的概率pk称为网络的度分布

(3)

N表示网络的节点规模,Nk表示度为k的节点规模。网络的平均度为

N.

(4)

从网络中任选一条边到达节点的度为k+1的概率记为qk,

(5)

其为网络的余度分布,即任选一条边到达节点的余度为k的概率[5-6]。生成函数是一种有效的数学工具,因此给出度分布及余度分布的概率生成函数

(6)

网络的另一个重要性质就是聚类特性,“物以类聚,人以群分”。聚类系数就是用来描述网络中节点聚集程度的度量,分为全局和局部聚类系数。在给出聚类系数的定义之前,先给出网络中二元组、三元组以及三角形的概念。在网络G中,称i-j为二元组(也称边或对),

若定义

(7)

其中i,j=1,2,…,N。类似地,在网络G中,如果节点i和j,节点j和h之间都有连边则称i-j-h为三元组,特别地,如果i和h互为邻居,则此三元组为三角形或闭三元组;否则为开三元组,其定义分别为

(8)

因此,网络中三元组,开三元组和三角形数量分别为

(9)

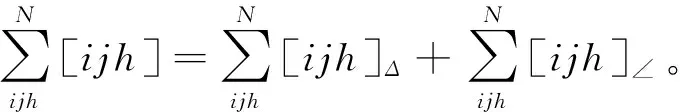
(10)

对于网络G的任意节点j,其度为kj,其邻居之间实际存在的边数Ej,则以该节点为中心的三角形数量为Ej,三元组数量为kj(kj-1)/2,则节点j的聚类系数定义为

(11)

除以上网络特性外,网络的一些特征之间也有相关性,如节点度、节点状态等。为定量刻画网络中节点间的相关性大小,有以下三类相关系数的定义:

(1) 不同状态节点之间的相关性：状态为A和C的节点间的相关系数[7]

(12)

其中,[AC]表示状态为A与状态为C节点间的实际连边数,[A]和[C]分别表示状态A和C的节点数。

(2) 不同度节点之间的相关性：度为k和l的节点间的相关系数[8]

(13)

其中,Nkl是度为k与l的节点间的实际连边数。

(3) 节点处于不同度和状态之间的相关性：状态为A度为k和状态为C度为m的节点间的相关系数[1]

(14)

其中,[Ak]表示状态为A度为k的节点数,[Cm]表示状态为C度为m的节点数,[AkCm]表示这两类节点间的实际连边数。

不同的网络结构有不同的网络拓扑特性,经典的网络有四种:规则网络、随机网络[2]、小世界网络[9]和无标度网络[3],表1给出了这四类网络度分布和聚类系数的特征。

表1 经典网络的度分布和聚类系数

规则网络的聚类系数大、随机网络度分布均匀聚类系数小,小世界网络的度分布均匀聚类系数大,而无标度网络的度分布异质但聚类不明显[1]。除了一般的随机网络,学者们经常用到的是广义的随机网络即配置网络[10],这类网络通过给定的度分布序列生成随机网络,当网络规模足够大时,聚类系数趋于零,即网络结构为类树结构。

以上介绍了网络中一些拓扑特征量的基本概念和具体的数学表达式,下面将对静态网络上的四类传播动力学模型(基于对关系、度、节点以及渗流理论的动力学模型)的建模思想、分析方法以及主要进展逐一介绍。本文用到的主要符号及含义如表2所示。

表2 本文的基本符号表

1 网络传播动力学模型

最基本的两类仓室模型为SIS和SIR模型[1],其中个体可处于易感S、染病I、恢复R三种状态。对于SIS类型的疾病,个体得病后还可以恢复成易感个体,而对于SIR类型的疾病,个体得病后恢复成永久免疫性个体。网络传播动力学将群体中的个体看成节点,个体与个体之间的接触看成边,研究网络结构和疾病或者信息共同演化的规律。基于不同的标准,网络传播动力学模型有不同的分类。如基于不同的网络,模型可分为规则网络、随机网络及无标度网络等动力学模型。基于网络度异质性,模型可以分为均匀网络模型,异质网络模型。基于网络结构是否随时间变化,模型可分为静态网络模型和动态网络模型。而基于建模角度和方法的不同,模型可以分为基于对关系、度、节点及渗流理论的动力学模型,下面分别介绍静态网络中的这四类模型。

1.1 基于对关系的动力学模型

考虑一个标准传染率的SIS均匀混合动力学模型

(15)

其中β和γ分别表示传染率和恢复率系数,[S]和[I]分别表示易感者和染病者的数量。显然,从网络的角度来看,均匀混合模型将网络看作是规则网络或者完全图,忽略了网络复杂的结构及其动态演化。基于对关系的动力学模型主要研究节点以及节点间的连边(对或二元组)随时间的动力学演化过程,下面从均匀网络和异质网络两个方面来介绍基于对关系的SIS动力学模型。

1.1.1 均匀网络上的对关系模型

考虑一个规模为N的网络,其中每个个体有两种不同的状态:易感状态S和染病状态I,则节点及节点之间连边的动力学方程为

=γ[II]-γ[SI]-β[SI]-β[ISI]+β[SSI],

(16)

其中,[SI]二元组表示易感和染病节点的连边数量,[SSI]代表三元组S-S-I的数量而[ISI]代表三元组I-S-I数量的二倍[7]。在模型(16)中单节点的变化依赖二元组的变化,二元组的变化又依赖三元组的变化,方程并不封闭。为了研究其动力学性态须在误差允许的范围内封闭方程,下面介绍几种封闭方程的逼近方法,分无聚类和有聚类两种。

1)无聚类的均匀网络三元组逼近

文献[12]提出了用一元组(即单节点)和二元组来近似表示三元组的方法。对于给定的无聚类网络,设节点状态分为A、B、C三种类型。对于状态为B的节点,若其邻居状态为A和C的节点数都服从泊松分布且相互独立,三元组可近似表示为

(17)

对于状态为B的节点,若其邻居状态为A和C的节点数服从多项分布,三元组可近似表示为

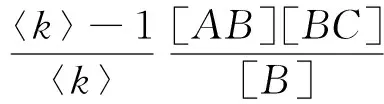
(18)

2)含聚类的均匀网络三元组逼近

在含聚类的网络中,文献[7,13-14]给出了均匀网络中三元组的近似表达式

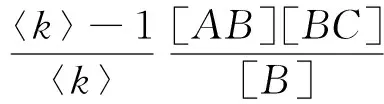
(19)

其中φ表示网络的全局聚类系数(见式(10)),CAC为状态相关系数(见式(12))。

1.1.2 异质网络上的对关系模型

与均匀网络相比,异质网络主要表现在节点度的差异性大,有的节点度非常大,有的则很小。而现实生活中大部分网络均为异质网络,为使模型更加准确地反映现实,考虑不同状态、不同度的节点间构成的二元组变化更加合理。因此,建立如下异质网络的对关系模型[15]

(20)

其中,K(K≤N)表示网络的最大度,[Sk]与[Ik]表示度为k的易感者和染病者的数量;正如表2所示,[SkSl],[SkSl],[SkSl]表示相应二元组的数量。同样地,要封闭模型(20),有两类异质网络逼近公式:1)异质网络三元组的逼近公式,分有无聚类两种情形[15];2)异质网络二元组的逼近公式。

1)异质网络三元组的逼近公式[15]

①无聚类的异质网络三元组逼近公式:不考虑聚类的影响,即φ=0时,异质网络三元组近似为

(21)

②含聚类的异质网络三元组逼近公式:考虑异质网络中三角形的影响,当φ≠0时,三元组近似为

(22)

其中CAkCm表示网络中度为k状态为A与度为m状态为C的节点之间的相关系数(见(14))。

2)异质网络二元组的逼近公式

①基于二元组的异质网络二元组的反卷积逼近公式:2002年,Eames和Keeling[15]基于性传播疾病,提出了二元组的反卷积逼近

(23)

其中,Ckl表示度为k和l节点之间的相关系数(见(13))。

②基于节点的异质网络二元组的反卷积逼近公式:2011年,House和Keeling[8]提出了基于节点的异质网络二元组的反卷积逼近

(24)

逼近公式(24)假设B状态节点连接到Ak型节点不依赖于Ak节点的度,即与网络的局部结构无关。紧对模型就是根据这一逼近公式得到,超紧对模型也是在紧对模型的基础上建立的,模型的维数更低[16]。

③基于同配混合的异质网络二元组的反卷积逼近公式:在同配混合的假设下,与公式(23)不同,文[8]也给出了二元组[AkBl]的逼近

(25)

这个逼近虽然保持了网络的同配性,却忽略了节点状态之间的联系。

注1.当度分布pk取Delta分布,即每个节点的度为常数k,模型(20)通过逼近公式(25)近似后的模型与均匀混合模型(15)一致,因此网络动力学模型考虑的更加细致。

注2.通过逼近公式(25),模型(20)变为方程

(26)

在度不相关的网络中,相关系数Ckl=1,则模型(26)与Pastor-Satorra等基于节点度的分类提出的异质平均场模型[4]一致,在1.2节对此将做详细介绍。

基于对关系的传播动力学模型不仅能描述网络中不同状态节点随时间的演化过程,而且能捕捉到不同状态节点间连边随时间的演化规律,通过模型中所含的网络拓扑参数来揭示网络结构对疾病传播的影响。然而,找到合适且精确的对逼近公式是对关系模型能否精确的关键,也是研究的挑战之一。Matsuda[17]在1992年首次提出对关系模型,之后Keeling[7],Rand[13],Eamse[15]等给出了不同的模型和逼近公式,Trapman[14]等讨论了网络结构对基本再生数的影响,Luo[18]等分析了均匀网络上的SIS对逼近模型的全局动力学性态。基于对关系的模型也推广到了异质网络[15]、有向网络[16]、加权网络[19]以及网络显示模体[20]、非马尔科夫过程传播[21]、紧对模型[8,22]、超紧对模型[23]、婚姻网络[24]等。

1.2 基于度的动力学模型

从对关系模型(26)看出,在度不相关的网络中,即相关系数Ckl=1时,通过基于同配混合的异质网络二元组的反卷积逼近公式(25)得到的对关系模型与Pastor-Satorra等基于节点度的分类提出的异质平均场模型[4,25]一致。基于节点度的动力学模型假设度相同的节点具有相同的动力学规律,这部分将介绍两种基于节点度的动力学模型:异质平均场模型和边仓室模型。

1.2.1 异质平均场模型

Pastor-Satorras等人首次用复杂网络来刻画个体间的接触信息,研究个体接触的异质性对疾病传播的影响[4]。在文献[4]中,假设相同度的节点有相同的动力学规律,然后应用平均场理论建立确定性模型来研究相同度节点的动力学过程。下面以SIS模型为例来介绍异质平均场模型。

设网络中度为k的节点中染病节点的密度为ρk,得到以下SIS异质平均场模型

(27)

即网络中任意一条边指向染病者的概率等于染病者发出的总边数占网络总边数的比例。从模型(27)得其基本再生数为

R0=β〈k2〉/〈k〉.

(28)

因此,疾病的传播阈值为βc=〈k〉/〈k2〉。当疾病的传染率小于传播阈值βc(或R0<1)时,疾病最终消失,而当疾病的传染率大于传播阈值βc(或R0>1)时,疾病流行。特别地,Pastor-Satorras等人发现在度分布为pk∝k-α的无标度网络中,当网络规模N→∞,幂指数2<α≤3时,疾病的传播阈值会消失,而均匀混合网络上始终存在有限阈值,这一发现颠覆了传统的有限传播阈值理论。

异质平均场模型通过网络度分布的信息,描述了度分布对传播动力学的影响,但忽略了聚类系数、团簇系数等网络拓扑结构的影响。此外,在度不相关的假设下,异质平均场模型被推广到SIR类型的疾病[27],带有人口动力学的动态网络[28],多菌株传染病[29],有向网络[30],加权网络等。文献[31]也给出了在度相关网络中SIS和SIR模型的疾病传播阈值,发现在无标度网络中,当网络规模N→∞,幂指数2<α≤3是疾病阈值消失的充分条件。

1.2.2 边仓室模型

传统的SIR仓室模型是按个体的状态将人群分为三种不同的类型(仓室):易感者, 染病者和恢复者人群,考虑了人群在各个仓室之间的转移。这类仓室模型的一个基本假设是人群是均匀混合的,忽略了个体单位时间内接触人数的异质性。而异质平均场模型考虑了个体接触的异质性,但模型的维数一般都比较高,增加了数学分析的难度。而边仓室模型[32-33]的出现弥补了传统仓室模型和异质平均场模型的不足。它借鉴仓室模型的思想,将边按照不同的类型分成三个不同的仓室,考虑不同边仓室之间的演化规律,得到一个低维的模型。下面详细介绍SIR边仓室模型[32-33]。

网络中易感者的比例等于从网络中随机抽取的一个测试节点i是易感者的概率,为计算此概率,边仓室模型做出如下假设:1) 测试节点i不会传染疾病给它的邻居;2) 节点i的邻居节点间相互独立,即假设网络的聚类很小;3) 节点间的度不相关,因此沿着一条边到达度为k的节点的概率为kpk/〈k〉。

设S(t),I(t),R(t)分别为网络中易感者、染病者和恢复者的比例;Θ(t)表示在t时刻,随机选择测试节点i,它的一个邻居节点j还没有把疾病传给i节点的概率。节点i是易感者意味着节点i的任意一个邻居都没有传染节点i,当节点i的度为k且其邻居节点间相互独立时,节点i是易感者的概率为Θk(t)。因此,网络中易感者的比例为

(29)

为得到Θ,在t时刻根据邻居节点j的状态分成三部分:1)邻居节点j是易感者的概率为ΦS;2)邻居节点j是染病者且没有传染节点i的概率为ΦI;3)邻居节点j是恢复者且没有传染节点i的概率为ΦR;则

Θ=ΦS+ΦI+ΦR.

(30)

各边仓室之间的流程图如图1所示。

Fig.1 Flow diagram for edge-based compartmental model[33]图1 边仓室模型流程图[33]

下面给出ΦS,ΦI和ΦR的求解过程。

由于节点的度不相关,节点i连接到度为k的邻居节点j的概率为kpk/〈k〉,同时节点i不会传染疾病给节点j,则度为k的j节点为易感者的概率为Θk-1。因此,

(31)

(32)

综上,可得边仓室模型为

S=G0(Θ),

I=1-S-R.

(33)

对于模型(33)由无病平衡点的局部渐近稳定性,得疾病的基本再生数为

(34)

(35)

边仓室模型仅用一维模型Θ的动力学方程便可以刻画疾病的动力学行为,其复杂程度与均匀混合模型一致,但可以将网络的度分布信息结合到模型中。然而,由于边仓室模型假设邻居节点间相互独立,因此它不适用于SIS类型的疾病[19],将边仓室模型推广到SIS类型的疾病传播是一个挑战性的工作。此外,利用反卷积逼近和三元组逼近公式

可以推出边仓室模型与基于对关系的动力学模型(36)等价[34]。

=β[SSI]-β[ISI]-β[SI]-β[SI].

(36)

边仓室模型也推广到含断边重连的动态网络[33],聚类网络[34],加权网络[35-36],带有人口动力学的动态网络[37]以及性传播与非性传播同时存在的疾病模型[38]等。

1.3 基于节点的动力学模型

在动力学传播模型中,一种考虑更精确的模型为基于节点的动力学模型,不同于对关系和度的动力学模型,该模型应用连续时间Markov链技术,充分考虑到每个节点的特征,深入研究网络的拓扑结构对传染病的影响。下面介绍VanMieghem[39]提出的基于节点(邻接矩阵)构建的病毒传播动力学模型。

2009年,VanMieghem[39]提出了基于节点的病毒传播动力学模型,分析了病毒在网络上的动力学传播过程。考虑一个包含N个节点L条边的简单无向连通图G,其邻接矩阵为A=(aij)N×N。染病节点i传染其一个邻居的速率为β>0,恢复率为γ>0,假定疾病的传染和恢复是两个独立的泊松过程。Xi(t)表示在t时刻节点i的状态,即

(37)

令Δt→0,得到随机SIS病毒动力学传播模型

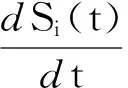
(38)

利用平均场的思想,对式(37)两边取均值E[Si(t)]=Pr[Xi(t)=1]=vi(t),得

(39)

对于式(39)右边的第三项

E[1{Xi(t)}=11{Xj(t)}=1]=Pr[Xi(t)=1,Xj(t)=1]=Pr[Xi(t)=1]Pr[Xj(t)=1|Xi(t)],

在网络连通的情况下,有Pr[Xj(t)=1|Xi(t)=1]≥Pr[Xj(t)=1],因为给定一个染病者节点i,不可能对其邻居节点j的染病概率有抑制作用。现假定随机变量1{Xi(t)=1}和1{Xj(t)=1}相互独立,即

E[1{Xi(t)}=11{Xj(t)}=1]=E[1{Xi(t)}=1]E[1{Xj(t)}=1].

(40)

令Δt→0,结合公式(39)和(40)得到确定性SIS病毒传播模型

(41)

方程(41)也称为N-intertwined SIS病毒传播模型。记V(t)=[v1(t),v2(t),…vN(t)],diag(vi(t))是对角元素为v1(t),v2(t),…,vN(t)的一个对角矩阵,则微分方程(41)相应的矩阵形式为

(42)

记邻接矩阵A的最大实特征值为λmax(A),对方程(42),只要初始值V(0)≠0,当有效传染率β/γ≤1/λmax(A)时,无病平衡点是全局渐近稳定的;当有效传染率β/γ>1/λmax(A)时,地方病平衡点也是全局渐近稳定的。

文献[39]对随机模型(38)与确定性模型(41)做了比较,得出平均场近似的N-intertwined SIS模型(41)高估了节点被传染的概率,原因是假定随机变量1{Xi(t)=1}和1{Xj(t)=1}相互独立。可以看出基于节点的随机SIS网络模型更加精确但难以数学处理,而确定性SIS模型可作为随机SIS模型的近似,且随着网络规模的增大,随机SIS网络模型与确定性SIS网络模型的解的差异减小。基于节点的动力学模型充分考虑了每个节点的特征,能深入研究网络的拓扑结构对传染病的影响,其建模的思想也推广到了其他的模型中,如病毒传播模型[40-41],有单病毒模型[42-46], 双病毒-单网络模型[47],双病毒-双网络模型[48-49]等,其中,文献[40-48]的病毒传播模型基于线性传播率,文献[49-51]的模型是基于非线性的传播率。

1.4 基于渗流理论的动力学模型

除了上面三类动力学模型,在复杂网络上研究传播动力学的另外一种方法是基于渗流理论的动力学模型,简称渗流模型。渗流是物理学中的一种叫法,在现实生活存在着许许多多的渗流现象。例如,在Internet上,由路由器组成的网络中,究竟哪些路由器不工作或者多大比例的路由器不工作会影响到Internet的正常运行呢?再比如,在疾病传播过程中,到底切断人与人之间的哪些传播途径或者切断多少能够抑制疾病的大规模流行?这些现象和问题都可以通过渗流模型来解释和研究[52]。

渗流分为点渗流和边渗流,点渗流主要研究随机选择的点被占用后形成的连通分支或巨连通分支对网络功能和结构的影响(见图 2(a),灰色的点为“占用点”),如研究网络对节点随机删除的弹性度 (Resilience)[53-54],而边渗流主要研究随机选择的边被占用后,由“占用边”连接的点形成的连通分支或巨连通分支对网络功能和结构的影响(见图 2(b),灰色的边为“占用边”),如研究疾病的流行阈值和最终规模等[55]。其中,连通分支(Component)为相互连通的占用点(或由占用边连接的点)形成的网络子图,如图 2(a)中1-6,3-4,8三个连通分支和图 2(b)中2-3-4-7,5-8两个连通子图,当连通分支包含了网络中相当比例的节点即连通分支的节点规模与网络的规模为同一数量级时这一连通分支称为巨连通分支(Giant Component)[56]。

Fig.2 (a) Site percolation (Grey occupied node); (b) Bond percolation (Bold-grey occupied edge)图2 (a)点渗流(灰色为占用点);(b)边渗流(灰色为占用边)

一般地,用“占用概率T”来表示网络中被占用点或边的比例。在点渗流中,正常的节点可以看成是被占用的节点(如图 2(a)的灰色节点)。关于点渗流,Cohen等发现在度分布服从幂率分布,pk～k-α(α<3)时,网络始终存在一个巨连通分支,即使点占用概率的临界值Tc等于或小于零,表明幂率网络对点随机删除有很强的鲁棒性[54]。对点渗流的其他研究和扩展见文献[53,57]。疾病的传播动力学主要通过边渗流来研究,因此下面主要回顾在不含聚类网络和含聚类网络上,边渗流模型在传播动力学中的研究进展。

1.4.1 不含聚类的边渗流模型

网络上的SIR传染病模型可以映射到边渗流模型中[55]。考虑染病节点i和它的一个易感邻居j,假定这两节点之间的平均传染率为βij,染病节点i的病程时间为τi,则疾病这这段时间内没有从节点i传染到节点j的概率为

(43)

因此,从节点i到节点j传染的概率为

Tij=1-e-βijτi.

(44)

传染率βij,染病时间τi分别服从分布P(β),P(τ)且相互独立,则每条边的平均传染概率,即边占用概率为

(45)

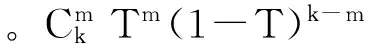
G1(x;T)=G1(1+(x-1)T).

(46)

H0(x;T)表示任选一点所属的连通分支(由占用边连接而成)规模分布的生成函数,H1(x;T)表示任选一条边到达的节点所属的连通分支(由占用边连接而成)规模分布的生成函数,

H0(x;T)=xG0(H1(x;T);T),

H1(x;T)=xG1(H1(x;T);T).

(47)

当网络中没有巨连通分支时,由式(47)得占用边连接的连通分支的平均规模,即疾病暴发的平均规模为

(48)

因此,

(49)

从式(49)得疾病的阈值为

(50)

当网络中出现巨连通分支,即边占用概率T>Tc时,由于H0(x;T)仅表示连通分支规模的分布,而网络由连通分支和巨连通分支组成,即

H0(1;T)=1-MR,

(51)

MR(T)表示巨连通分支规模(由占用边连接而成)占整个种群规模的比例。因此,流行病的最终规模为

MR(T)=1-G0(u;T),

u=G1(u;T).

(52)

u为沿着一条单边到达的节点不属于由占用边连接而成的巨连通分支的概率。

综上,可以看出边渗流模型和SIR传染病相对应的量分别是:渗流相变阈值对应传染病的流行阈值,连通分支(由占用边连接的点形成)的分布对应传染病暴发规模的分布,阈值之上形成的巨连通分支对应传染病流行的最终规模。在时间取极限,网络规模无限大时,边渗流模型可以提供传染病的流行规模,但目前渗流还不能反映流行病随时间的演化特性。此外,对于异质的染病时间分布,Kenah[58],Miller[59]给出了相应的流行病阈值,平均暴发规模,流行病最终规模。

当占用概率T=1时,如文献[6]所述,H0(x)表示整个网络中随机任选一节点所属连通分支规模的概率生成函数,即网络中所有的边被占用,H0(x;1)=H0(x);H1(x)表示任选一条边到达节点所属连通分支规模的概率生成函数,H1(x;1)=H1(x),这样可得到整个网络连通分支的平均规模,巨连通分支规模在网络中所占的比例及阈值。以上结果在不含聚类的配置网络中得到,但现实网络一般都含有聚类,因此Newman将渗流推广到含聚类的网络中。

1.4.2 含聚类的边渗流模型

2009年,Newman构建了有三角形的弱聚类配置网络[11],如图3所示。所谓弱聚类网络是指三角形之间无重边数或很小,而强聚类网络指边的重数大,多个三角形共享一条边[60]。

Fig.3 Illustration of network with weak clustering图3 弱聚类网络示意图[6]

在该弱聚类网络中,每个节点有两种度:单边和三角形。定义网络的联合度分布pst为网络中有s条单边,t个三角节点的比例,显然该类节点的度为k=s+2t,因此网络的度分布为

(53)

其中,δij为Delta函数。联合度分布pst和度分布pk的生成函数分别为

(54)

(55)

进一步定义节点的余度分布qst,rst,

(56)

其中,qst表示沿着一条单边到达一个节点,其剩余边数为s,三角形数为t的概率;qst表示沿着一个三角形到达一个节点,其单边数为s,剩余三角形数为t的概率,〈s〉,〈t〉为相应的均值。两余度分布对应的生成函数为

(57)

下面利用以上变量计算聚类网络巨连通分支的规模,定义u1为沿着一条单边到达的节点不属于巨连通分支的概率,v1沿着一个三角形到达的节点不属于巨连通分支的概率,则

(58)

同样用MR表示巨连通分支规模占整个网络的比例,则

(59)

文献[11]同样给出了相变的阈值条件

(60)

当网络中三角形为零时,该阈值条件变回到原始阈值条件(当Tc=1时见式(50))。

类似于无聚类网络[55],当边占用概率为T时,u2为沿着一条单边到达的节点属于连通分支(由占用边连接而成)的概率,v2沿着一个三角形到达的节点属于连通分支(由占用边连接而成)的概率,则流行病的最终规模MR(T)为

(61)

Newman发现当该弱聚类网络的平均度(总度的平均度)不变,增加聚类系数时疾病的阈值增加,流行病最终规模减小[11]。Newman在强聚类的二部图投影网络中,也发现了同样的结果[61]。而Miller却发现与相同联合度分布和相同度度相关性的无聚类网络相比,弱聚类网络中疾病阈值和疾病的流行规模都减小[62]。Gleeson构建了含有团(Clique)的聚类网络,发现与Miller同样的结果[63]。那么,聚类的增加到底是促进疾病阈值还是抑制呢?我们得出聚类对疾病阈值的影响是双重的既可以增加阈值又可以减少阈值[64]。

2 结论

网络上的疾病或信息传播动力学作为复杂网络研究中的重要课题,具有非常重要的意义。通过网络传播动力学模型来研究疾病或信息在网络上的传播过程,有助于弄清网络结构和疾病或信息的耦合动力学演化机制,揭开网络结构(如度分布,度异质性、度相关性,状态相关性、聚类等)对疾病或信息传播影响的面纱,进而为制定疾病预防控制策略和网络舆情控制提供指导。

本文介绍了静态网络上基于对关系、度、节点和渗流理论4类传播动力学模型的建模思想和分析方法,并探究了各类模型的优势和局限性。基于对关系,节点的动力学模型和基于度的异质平均场模型,既可以研究SIS模型也可以研究SIR模型,而基于度的边仓室模型和渗流模型仅适用于SIR模型。基于节点的动力学模型,利用Markov链和网络的邻接矩阵考虑了每个节点的动力学过程,比对关系和度的动力学模型更精群,但数学分析比较困难。此外,基于渗流理论的模型不同于另外三种模型,可以给出SIR流行病的阈值,流行病最终规模,但不能描述动力学的时间演化过程,并且仅仅适用于SIR模型。动态网络[28]、耦合网络[65]、多层网络[66]上的传播动力学研究也有一定的研究成果,总之网络上疾病和信息的传播动力学研究在今后仍将是研究热点,并将广泛的推广到实际应用中。

致谢：研究生荆文君、曹晓春、冯姗姗及王宁宁在整理文献和论文的撰写过程中所做的工作。

[1] 靳祯,孙桂全,刘茂省.网络传染病动力学建模与分析[M].北京：科学出版社, 2014.

[2] Erdös P,Rényi A.On the Evolution of Random Graphs[J].PublicationsoftheMathematicalInstituteoftheHungarianAcademyofSciences,1960,5:17-61.

[4] Pastor-Satorras R,Vespignani A.Epidemic Spreading in Scale-free Networks[J].PhysicalReviewLetters,2000,86(14):3200.DOI:10.1103/PhysRevLett.86.3200.

[5] 史定华.网络度分布理论[M].北京：高等教育出版社,2011.

[6] Newman M E J,Strogatz S H,Watts D J.Random Graphs with Arbitrary Degree Distributions and Their Applications[J].PhysicalReviewE,2001,64(2):026118.DOI:10.1103/PhysRevE.64.026118.

[7] Keeling M J.The Effects of Local Spatial Structure on Epidemiological Invasions[J].ProceedingsoftheRoyalSocietyofLondonB:BiologicalSciences,1999,266(1421):859-867.DOI:10.1098/rspb.1999.0716.

[8] House T,Keeling M J.Insights from Unifying Modern Approximations to Infections on Networks[J].PhysicalReviewDParticles&Fields,2011,8(54):67-73.DOI:10.1098/rsif.2010.0179.

[9] Watts D J,Strogatz S H.Collective Dynamics of ‘small-world’ Networks[J].Nature,1998,393(6684):440-442.DOI:10.1038/30918.

[10] Bender E A,Canfield E R.The Asymptotic Number of Labeled Graphs with Given Degree Sequences[J].JournalofCombinatorialTheory,SeriesA,1978,24(3):296-307.DOI:10.1016/0097-3165(78)90059-6.

[11] Newman M E J.Random Graphs with Clustering[J].PhysicalReviewLetters,2009,103(5):058701.DOI:10.1103/PhysRevLett.103.058701.

[12] Morris,John A,Morris,etal.Representing Spatial Interactions in Simple Ecological Models[D].University of Warwick,1997.

[13] Rand D A.Correlation Equations and Pair Approximations for Spatial Ecologies[J].AdvancedEcologicalTheory:PrinciplesandApplications,1999,100.

[14] Trapman P.Reproduction Numbers for Epidemics on Networks using Pair Approximation[J].MathematicalBiosciences,2007,210(2):464-489.DOI:10.1016/j.mbs.2007.05.011.

[15] Eames K T D,Keeling M J.Modeling Dynamic and Network Heterogeneities in the Spread of Sexually Transmitted Diseases[J].ProceedingsoftheNationalAcademyofSciencesoftheUnitedStatesofAmerica,2002,99(20):13330-5.DOI:10.1073/pnas.202244299.

[16] Sharkey K J,Fernandez C,Morgan K L,etal.Pair-level Approximations to the Spatio-temporal Dynamics of Epidemics on Asymmetric Contact Networks[J].JournalofMathematicalBiology,2006,53(1):61-85.DOI:10.1007/s00285-006-0377-3.

[17] Matsuda H,Ogita N,Sasaki A,etal.Statistical Mechanics of Population The Lattice Lotka-Volterra Model[J].ProgressofTheoreticalPhysics,1992,88(6):1035-1049.DOI:10.1143/PTP.88.1035.

[18] Luo X F,Zhang X,Sun G Q,etal.Epidemical Dynamics of SIS Pair Approximation Models on Regular and Random Networks[J].PhysicaAStatisticalMechanics&ItsApplications,2014,410(12):144-153.DOI:10.1016/j.physa.2014.05.020.

[19] Rattana P,Blyuss K B,Eames K T,etal.A Class of Pairwise Models for Epidemic Dynamics on Weighted Networks[J].BulletinofMathematicalBiology,2013,75(3):466.DOI:10.1007/s11538-013-9816-7.

[20] House T,Davies G,Danon L,etal.A Motif-Based Approach to Network Epidemics[J].BulletinofMathematicalBiology,2009,71(7):1693-1706.DOI:10.1007/s11538-009-9420-z.

[21] Kiss I Z,Röst G,Vizi Z.Generalization of Pairwise Models to non-Markovian Epidemics on Networks[J].PhysicalReviewLetters,2015,115(7):487-494.DOI:10.1103/PhysRevLett.115.078701.

[22] Sherborne N,Blyuss K B,Kiss I Z.Compact Pairwise Models for Epidemics with Multiple Infectious Stages on Degree Heterogeneous and Clustered Networks[J].JournalofTheoreticalBiology,2016,407:387-400.DOI:10.1016/j.jtbi.2016.07.015.

[23] Simon P L,Kiss I Z.Super Compact Pairwise Model for SIS Epidemic on Heterogeneous Networks[J].JournalofComplexNetworks,2016,4(2):187-200.DOI:10.1093/comnet/cnv018.

[24] Pei X,Zhan X X,Jin Z.Application of Pair Approximation Method to Modeling and Analysis of a Marriage Network[J].AppliedMathematics&Computation,2017,294:280-293.DOI:10.1016/j.amc.2016.09.010.

[25] Wang W,Tang M,Eugene S H,etal.Unification of Theoretical Approaches for Epidemic Spreading on Complex Networks[J].ReportsonProgressinPhysicsPhysicalSociety,2016,80(3):036603.DOI:10.1088/1361-6633/aa5398.

[26] Pastor-Satorras R,Vespignani A.Epidemic Dynamics and Endemic States in Complex Networks[J].PhysicalReviewE,2001,63(6):066117.DOI:10.1103/PhysRevE.63.066117.

[27] Moreno Y,Pastor-Satorras R,Vespignani A.Epidemic Outbreaks in Complex Heterogeneous Networks[J].TheEuropeanPhysicalJournalB,2002,26(4):521-529.DOI:10.1140/ejpb/e20020122.

[28] Jin Z,Sun G,Zhu H.Epidemic Models for Complex Networks with Demographics[J].MathematicalBiosciencesandEngineering,2014,11(6):1295-1317.DOI:10.3934/mbe.2014.11.1295.

[29] Masuda N,Konno N.Multi-state Epidemic Processes on Complex Networks[J].JournalofTheoreticalBiology,2006,243(1):64-75.DOI:10.1016/j.jtbi.2006.06.010.

[30] Wang J,Liu Z.Mean-field Level Analysis of Epidemics in Directed Networks[J].JournalofPhysicsAMathematical&Theoretical,2009,42(35):355001.DOI:10.1088/1751-8113/42/35/355001.

[32] Miller J C.A Note on a Paper by Erik Volz:SIR Dynamics in Random Networks[J].JournalofMathematicalBiology,2011,62(3):349-358.DOI:10.1007/s00285-010-0337-9.

[33] Miller J C,Slim A C,Volz E M.Edge-based Compartmental Modelling for Infectious Disease Spread[J].JournaloftheRoyalSocietyInterface,2012,9(70):890-906.DOI:10.1098/rsif.2011.0403.

[34] Volz E M,Miller J C,Galvani A,etal.Effects of Heterogeneous and Clustered Contact Patterns on Infectious Disease Dynamics[J].PlosComputationalBiology,2011,7(6):e1002042.DOI:10.1371/journal.pcbi.1002042.

[35] Rattana P,Miller J C,Kiss I Z.Pairwise and Edge-based Models of Epidemic Dynamics on Correlated Weighted Networks[J].MathematicalModellingofNaturalPhenomena,2011,9(2):58-81.DOI:10.1051/mmnp/20149204.DOI:10.1051/mmnp/20149204.

[36] Wang W,Tang M,Zhang H F,etal.Epidemic Spreading on Complex Networks with General Degree and Weight Distributions[J].PhysicalReviewE,2014,90(4-1):042803.DOI:10.1103/PhysRevE.90.042803.

[37] Millera J C,Slim A C.Modeling Disease Spread in Populations with Birth,Death,and Concurrency[J].arXivPreprintarXiv:1611.04800,2016.

[38] Miller J C.Mathematical Models of SIR Disease Spread with Combined Non-sexual and Sexual Transmission Routes[J].InfectiousDiseaseModelling,2017,2(1):35-55.DOI:10.1016/j.idm.2016.12.003.

[39] Van Mieghem P,Omic J,Kooij R.Virus Spread in Networks[J].IEEE/ACMTransactionsonNetworking(TON),2009,17(1):1-14.DOI:10.1109/TNET.2008.925623.

[40] Youssef M,Scoglio C.An Individual-based Approach to SIR Epidemics in Contact Networks[J].JournalofTheoreticalBiology,2011,283(1):136-144.DOI:10.1016/j.jtbi.2011.05.029.

[41] Sahneh F D,Scoglio C,Van Mieghem P.Generalized Epidemic Mean-field Model for Spreading Processes Over Multilayer Complex Networks[J].IEEE/ACMTransactionsonNetworking,2013,21(5):1609-1620.DOI:10.1109/TNET.2013.2239658.

[42] Yang L,Draief M,Yang X.Heterogeneous Virus Propagation in Networks:A Theoretical Study[J].MathematicalMethodsintheAppliedSciences,2017,40(5):1396-1413.DOI:10.1002/mma.4061.

[43] Yang L X,Draief M,Yang X.The Impact of the Network Topology on the Viral Prevalence:A Node-based Spproach[J].PloSOne,2015,10(7):e0134507.DOI:10.1371/journal.pone.0134507.

[44] Sahneh F D,Scoglio C.Epidemic Spread in Human Networks[C].Decision and Control and European Control Conference (CDC-ECC),2011:3008-3013.

[45] Sahneh F D,Chowdhury F N,Scoglio C M.On the Existence of a Threshold for Preventive Behavioral Responses to Suppress Epidemic Spreading[J].ScientificReports,2012,2:632.DOI:10.1038/srep00632.

[46] Liu J,Paré P E,Nedic＇A,etal.On the Analysis of a Continuous-time Bi-virus Model[C].Decision and Control (CDC),2016:290-295.

[47] Sahneh F D,Scoglio C.Competitive Epidemic Spreading Over Arbitrary Multilayer Networks[J].PhysicalReviewE,2014,89(6):062817.DOI:10.1103/PhysRevE.89.062817.

[48] Yang L X,Yang X,Wu Y.The Impact of Patch Forwarding on the Prevalence of Computer Virus:A Theoretical Assessment Approach[J].AppliedMathematicalModelling,2017,43:110-125.DOI:10.1016/j.apm.2016.10.028.

[49] Xu S,Lu W,Zhan Z.A Stochastic Model of Multivirus Dynamics[J].IEEETransactionsonDependableandSecureComputing,2012,9(1):30-45.DOI:10.1109/TDSC.2011.33.

[50] Xu S,Lu W,Xu L.Push-and Pull-based Epidemic Spreading in Networks:Thresholds and Deeper Insights[J].ACMTransactionsonAutonomousandAdaptiveSystems(TAAS),2012,7(3):32.DOI:10.1145/2348832.2348835.

[51] Xu S,Lu W,Xu L,etal.Adaptive Epidemic Dynamics in Networks:Thresholds and Control[J].ACMTransactionsonAutonomousandAdaptiveSystems(TAAS),2014,8(4):19.DOI:10.1145/2555613.

[52] Newman M E J.Networks:An Introduction[M].United Slates:Oxford University Press Inc.,New York,2010,1-2.

[53] Callaway D S,Newman M E J,Strogatz S H,etal.Network Robustness and Fragility:Percolation on Random Graphs[J].PhysicalReviewLetters,2000,85(25):5468.DOI:10.1103/PhysRevLett.85.5468.

[54] Cohen R,Havlin S,Ben-Avraham D.Efficient Immunization Strategies for Computer NetWorks and Populations[J].PhysicalReviewLetters,2003,91(24):247901.DOI:10.1103/PhysRevLett.91.247901.

[55] Newman M E J.Spread of Epidemic Disease on Networks[J].PhysicalReviewE,2002,66(1):016128.DOI:10.1103/PhysRevE.66.016128.

[56] 汪小帆,李翔,陈关荣.网络科学导论[M].北京：高等教育出版社,2012，406：387-482.

[57] Albert R.Attack and Error Tolerance in Complex Networks[J].Nature,2000,406:387-482.

[58] Kenah E,Robins J M.Second Look at the Spread of Epidemics on Networks[J].PhysicalReviewE,2007,76(3):036113.DOI:10.1103/PhysRevE.76.036113.

[59] Miller J C.Epidemic Size and Probability in Populations with Heterogeneous Infectivity and Susceptibility[J].PhysicalReviewE,2007,76(1):010101.DOI:10.1103/PhysRevE.76.010101.

[60] Serrano M,Boguna M.Clustering in Complex Networks.I.General Formalism[J].PhysicalReviewE,2006,74(5):056114.DOI:10.1103/PhysRevE.74.056114.

[61] Newman M E J.Properties of Highly Clustered[J].PhysicalReviewE,2003,68(2):026121.

[62] Miller J C.Percolation and Epidemics in Random Clustered Networks[J].PhysicalReviewE,2009,80(2):020901.DOI:10.1103/PhysRevE.80.020901.

[63] Gleeson J P,Melnik S,Hackett A.How Clustering Affects the Bond Percolation Threshold in Complex Networks[J].PhysicalReviewE.81,2010,066114.DOI:10.1103/PhysRevE.81.066114.

[64] 李淑萍.网络拓扑结构对传播的影响研究[D].太原：中北大学,2015.

[65] Pan W,Sun G Q,Jin Z.How Demography-driven Evolving Networks Impact Epidemic Transmission Between Communities[J].JournalofTheoreticalBiology,2015,382:309-319.

[66] 张晓光.网络拓扑结构与传播动力学分析[D].太原：中北大学,2014.

Advances in Spreading Dynamics Research on Complex Networks

JIN Zhen1,2，LUO Xiaofeng1,3

(1.Complex System Research Center,Shanxi University,Taiyuan,Shanxi 030006,China;2.Shanxi Key Laboratory of Methods of Disease Prevention and Control and Big Data analysis, Shanxi University,Taiyuan,Shanxi 030006, China;3.School of Computer and Information Technology, Shanxi University, Taiyuan, Shanxi 030006,China)

Information or epidemic spread on networks is one of the hot issues in complex network research fields. It is a coupled dynamic process of diseases propagation and network evolution which depends on not only the transmission characteristics of information or epidemics themselves but also network structure and evolution, resulting in very complicated dynamic phenomena. The paper mainly focuses on some basic concepts, modelling and studying methods in respect to spreading dynamics on complex networks, containing 4 kinds of dynamic models——pair-based, degree-based, node-based and percolation theory-based models——and some advances in dynamic modelling and analyzing respects on complex networks.

complex networks;pair approximation;adjacent matrix;edge compartment;percolation theory

10.13451/j.cnki.shanxi.univ(nat.sci.).2017.03.006

2017-06-14；

2017-06-25

国家自然科学基金重点项目(11331009)；国家自然科学基金面上项目(11501340；11301491)；山西省回国留学人员科研资助项目(2014-020)；山西大学人才引进项目

靳祯(1965-)，男，博士生导师，教授，研究方向：生物动力学系统，复杂网络传播动力学等。E-mail:jinzhn@263.net

O175

A

0253-2395(2017)03-0426-16